Методика обучения решению задач на построение сечений многогранников в 10-11 классах
 Федеральное агентство по образованию Р.Ф. ПГПУ им. В. Г. Белинского
Федеральное агентство по образованию Р.Ф. ПГПУ им. В. Г. Белинского
Курсовая работа на тему:
«Методика обучения решению задач на построение сечений многогранников в 10-11 классах»
Выполнила:
студентка группы ми-51
Комисарова Л.П.
Проверила:
Финогеева И.С.
Пенза, 2007 г.
В стереометрии наряду с задачами на доказательство и вычисление решаются задачи на построение, но подход к методике изучения несколько иной, чем в планиметрии.
Задачи на построение в пространстве решаются двумя методами:
1) Задачи на воображаемое построение или задачи на доказательство существования фигур;
2) Задачи на проекционном чертеже.
В процессе решения задач на построение в воображении устанавливается лишь факт существования решения, само же построение искомого элемента не выполняется. По идее метода элементы, определяемые условием задачи, не задаются непосредственно в пространстве, ни на плоском чертеже, а удерживается в воображении. Решение задачи сводится к перечислению такой совокупности геометрических операций, фактическое выполнения которых (в случае если их можно было выполнить) приводит к построению искомого элемента. Задача считается решенной, если удается отыскать рассматриваемую совокупность построений.
При выполнении «воображаемых» построений считаем, что, во-первых, умеем строить плоскость, если заданы определяющие ее элементы (три точки, не лежащие на одной прямой, или прямая и точка вне ее, или две пересекающиеся прямые, или две параллельные прямые), и, во-вторых, в любой плоскости умеем осуществить все те построения, которые обоснованы в планиметрии. Так, если требуется провести через данную прямую а произвольную плоскость, берут произвольную точку А вне прямой а (возможность выбора такой точки также постулируется) и считают, что искомая плоскость проведена через прямую а и точку А.
Проиллюстрируем прием решения задач на построение в воображении на примере решения следующей задачи.
Задача 1. Построить плоскость, параллельную данной плоскости и проходящей через данную точку В
Решение. Допустим, что точка В не лежит в плоскости . Решение задачи в этом случае свелось бы к перечислению следующей совокупности построений:
1) в плоскости проводим две пересекающиеся прямые a и b;
2) через прямую а и точку В проводим плоскость 1;
3) в плоскости 1 через точку В проводим прямую a1, параллельную прямой а;
4) через прямую b и точку В проводим плоскость 2;
5) в плоскости 2 через точку В проводим прямую b1, параллельную прямой b;
6) через две пересекающиеся прямые a1 и b1 проводим плоскость . плоскость – искомая.
Чертеж при решении в воображении задач на построение может не выполняться. В тех же случаях, когда к нему прибегают, он играет вспомогательную роль: чертеж необходим только для облегчения работы воображения, когда пространственное воображение плохо развито или когда построения оказываются громоздкими.
В учебнике такие задачи решаются в разделах параллельные и перпендикулярные прямые и плоскости в пространстве в 10 классе, и большинство из них даны с решением (чаще всего просто построение, без анализа, доказательства, без исследования).
При решении задач на построение на проекционном чертеже элементы, определяемые условием задачи, задаются на изображении оригинала (точки, линии, плоскости, геометрические тела пространства в любой из материальных реализаций или воображаемые). Для эффективного решения задач на построение используются полные изображения, построение на которых выполняются без какой бы то ни было степени произвола.
Решение «Задачи 1» на проекционном чертеже выполняется следующим образом.
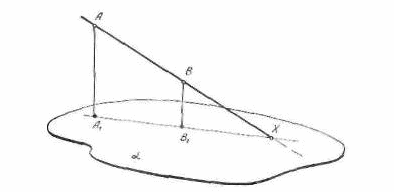
Рис. 1
Решение. Элементы, определяемые условием задачи, задаются на изображении так, как это выполнено на рисунке 1:
В плоскости (1) строим АМ (А1М) и AN (А1 N). В соответствии с условиями проекционного чертежа прямые АМ (А1М) и AN (А1 N) служат прямыми, принадлежащими плоскости(1). C помощью линейки и угольника проводим через прямые BN1 (B1N1) и BM1 (B1M1), параллельные прямым АМ (А1М) и AN (А1 N). Такие прямые строятся единственным образом и действительно изображают прямые, параллельные прямым АМ (А1М) и AN (А1 N). Пересекающиеся прямые BN1 (B1N1) и BM1 (B1M1) определяют искомую плоскость .
Рис.2
Обучение решению задач на построение на проекционном чертеже служит активным и гибким средством развития пространственного воображения учащихся.
Практика решения задач на построение на проекционном чертеже облегчает учащимся усвоении стереометрии. Развивает навыки в построении изображений, облегчает понимание курса черчения.
Однако до настоящего времени не закончена разработка методики изучения этого материала в школе. Требует уточнения объем материала, подлежащего изучению. Не определено и место изучения этих задач в школе.
Как показал опыт преподавания, обучение решению задач на построение лучше начинать с обучения решению задач на проекционном чертеже, так как понимание этих задач не требует хорошо развитого пространственного воображения учащихся. Более того, в процессе решения этих задач пространственное воображение настолько развивается. Что с определенного момента учащимся становится посильно освоение задач на построение, решаемых в воображении. В этом случае учащиеся после знакомства с новым методом на примере решения одной- двух задач остальные решают самостоятельно.
Чтобы получить проекционный чертеж, позволяющий конструктивно определить общие элементы изображенных прямых и плоскостей, т. е. решить на изображении так называемые позиционные задачи, достаточно задать, кроме изображения точек, прямых, плоскостей и вообще пространственных фигур на плоскости чертежа, изображения их проекций на некоторую плоскость, называемую основной.
Такой проекционный чертеж получается в результате двойного проектирования: точки А, В, С, D пространства проектируются на основную плоскость а, затем вместе с этой плоскостью, со своими проекциями на ней А', В', О, D' и проектирующими прямыми (АА\ ВВ', СО, DD') проектируются на плоскость чертежа (рис. 3, б).
Рис.3
Обучение решению задач на построение на проекционном чертеже строится так, чтобы учащиеся знакомились с этими задачами в порядке возрастающей трудности, и так, чтобы ранее решаемые задачи в основном подготавливали учащихся к пониманию решения последующих задач. Последнее достигается тем, что в работе рассматриваются следующие типы задач:
задачи, решаемые при введении проекционного чертежа;
задачи- упражнения по текущему материалу;
задачи на построение точек и линий пересечения прямых и плоскостей;
программные задачи на построении;
задачи на построение сечений.
Задачи на проекционном чертеже
Под решением задач на проекционном чертеже понимают решение позиционных и метрических задач на полном изображении.
Введением понятия о проекционном чертеже удобно выполняется в нижеприведенной последовательности. Наиболее подходящим моментом для проведения такой работы являются уроки, непосредственно следующие за уроками, на которых доказывалась первая теорема существования и на которых учащиеся познакомились с методами построения изображений планиметрических оригиналов.
В классе устанавливается, что на чертеже точка плоскости служит изображением не только точки оригинала, но и прямой (проектирующей). Прямая плоскости может изображать не только прямую, но и плоскость (проектирующую). Параллельные прямые плоскости изображают не только параллельные прямые оригинала, но и скрещивающиеся прямые, лежащие в параллельных проектирующих плоскостях, равно как и сами эти плоскости. Четыре точки плоскости изображений представляют, например, изображение как четырех точек одной плоскости оригинала, так и четырех точек не лежащих в одной плоскости. Внимание учащихся обращается и на тот факт, что по чертежу невозможно составить представление об относительном взаимном расположении изображенных на плоскости точки и прямой, точки и плоскости, прямой и плоскости и т.п. невозможно судить о принадлежности точек к прямым и плоскостям, прямых к плоскостям.
С неопределенностью рассматриваемых изображений можно знакомить учащихся сразу после введения понятия об изображении.
Перед введением проекционного чертежа все эти факты следует обобщить.
В качестве цели учащимся указывается на необходимость отыскания такого способа построения изображений пространственных фигур, при котором только по изображению можно было бы с безусловной необходимостью судить о взаимном расположении точек, прямых и плоскостей пространства. Прием построения изображений должен быть таким, чтобы только по изображению позволял бы определить, параллельны или непараллельны прямые оригинала, скрещиваются они или пересекаются, принадлежит точка прямой или плоскости, прямая- плоскости.
Далее учащимся сообщается, что сформулированных целей можно достигнуть, если изображения пространственных фигур, как и изображения плоских оригиналов, строить по базису с привлечением свойств изображения.
Сначала вводим понятие о базисе в оригинале и на изображении и показываем, что для построения изображения достаточно эффективно спроектировать лишь базисные точки оригинала. Далее раскрываем содержание второй теоремы существования.
К понятию проекционного чертежа можно прийти, если получить изображение одной из моделей обозначения точек в пространстве по базису и с привлечением свойств изображений.
Рассмотрим возможности осуществления этого пути на примере моделей обозначения точек с помощью основной плоскости.
Фиксировав базисные точки, строим моделей обозначения точек изображение точки. Показываем, что на таком чертеже может быть построено, и единственным образом, изображение любой наперед заданной точки оригинала.
Обосновывается и обратное утверждение, что в случае если изображение точки будет представлено вместе с основанием проектирующего отрезка на основной плоскости, то при фиксированном базисе изображение определяет единственную точку.
Как результат проведенных построений дается определение заданной точки: «Точка называется заданной на изображении, если при фиксированных базисах она является изображением единственной точки оригинала».
На построенном нами изображении заданными окажутся не только те точки, изображение которых предварительно было построено по оригиналу, но и те точки, для которых одна из точек плоскости принята за изображение собственно точки оригинала, а другая – за изображение ее основания.
Полученный таким образом проекционный чертеж представляет метрически определенное изображение.
Прямые плоскости оказываются заданными на изображении в том же смысле, что и точка.
Введение проекционного чертежа и решение задач на построение на нем не должно рассматриваться как два отдельных этапа обучения.
Одной из трудностей обучения решению задач на построение на проекционном чертеже является отсутствие в существующей учебной литературе достаточного числа четко выделенных простейших задач, овладение которыми обеспечивало бы понимание учащимися приемов решения более сложных задач. Кроме того, в методике не определилось еще число достаточно принципов, которыми можно было бы руководствоваться при отыскании решения задач.
Достижением осознанного понимания изучаемого материала при любой структуре обучения станет возможным, если решение задач не будет ограничиваться только механическим выполнением построений. От учащихся необходимо требовать устных пояснений по ходу выполняемых построений, аргументированного обоснования их. Следует также добиваться, чтобы и построения, проводимые в контрольных работах, сопровождались письменными объяснениями.
Задачи, решаемые при введении проекционного чертежа
Первой группой таких задач является упражнения, раскрывающие, что неопределенность восстановления оригинала по чертежу устранена на проекционном чертеже. Учитель показывает, что на проекционном чертеже «точка» изображает только точку оригинала, «прямая» - прямую, «плоскость» - плоскость.
На проекционном чертеже становится возможным определять только по изображению взаимное расположение точек, прямых и плоскостей. В порядке упражнения с учащимися рассматриваются способы изображения различных случаев взаимного расположения точки и основной плоскости.
В ходе упражнений учащимся сообщаются и новые необходимые определения.
В этот период следует дать определения «следа» прямой и заданной плоскости. Определения записываются в тетради.
Определение. Следом заданной прямой (плоскости) на основной плоскости называется точка (прямая) пересечения прямой (плоскости) с основной плоскостью.
В итоге обучения решению этих задач учащихся следует познакомить с двумя принципами, на основе которых выполняется построение точек пересечения прямой с плоскостью и построение прямой, по которой пересекаются плоскости.
1) для построения линий пересечения двух плоскостей достаточно знать две точки прямой, по которой пересекаются плоскости, или одну точку и направление прямой. Точки прямой, по которой пересекаются плоскости, определяются как точки пересечения произвольной прямой одной из заданных плоскостей с другой плоскостью.
2) для построения точки пересечения прямой с плоскостью достаточно построить линию пересечения произвольной вспомогательной плоскости, проведенной через данную прямую, с данной плоскостью. Точка пересечения данной прямой с данной плоскостью определяется как точки пересечения данной прямой с линией пересечения вспомогательной и данной плоскостей.
рис. 4
Задача: Построить точку пересечения данной прямой АВ (А1В1) с основной плоскостью
Решением этой задачи является точка пересечения (если она существует) прямых АВ и А1В1, так как в оригинале эти прямые лежат в одной и той же проектирующей плоскости.
При определении точек пересечения прямых полезно приучать учащихся с первых же шагов рассматривать построения на проекционном чертеже как проекцию соответственных построений в одной из материальных реализаций оригинала и устанавливать принадлежность или непринадлежность рассматриваемых прямых одной и той же плоскости оригинала. В данном случае, например, построение точки пересечения прямых АВ и А1В1 можно рассматривать как проекцию построений на листе фанеры, представляющим проектирующую плоскость АА1ВВ1.
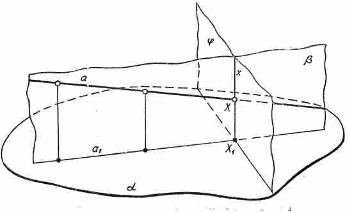
Задача. Построить (рис.5а) точку пересечения произвольно заданной прямой а(а1) с проектирующей плоскостью φ.
Рис.5а
Для решения задачи проводим через заданную прямую а(а1) вспомогательную проектирующую плоскость и строим линию (х) пересечения вспомогательной и заданной проектирующих плоскостей. Точка Х(Х1) —точка пересечения прямых х и а на изображении— является изображением точки пересечения этих прямых, так как в оригинале эти прямые лежат в одной плоскости. Вместе с тем точка Х(Х1) будет точкой пересечения прямой а(а1) с проектирующей плоскостью φ.
В самом деле, точка Х(Х1) принадлежит прямым а(а1) и х. Прямая х, как линия пересечения плоскостей β и φ, принадлежит плоскости φ. Следовательно, и точка X(X1) принадлежит плоскости φ,т.е. действительно точка X(Х1) является точкой пересечения прямой a(a1) и заданной плоскости.
Сначала при выполнении чертежей 'полезно обозначать вспомогательные плоскости обрывами и обрезами так, как это сделано на рис. Позже, чтобы не загромождать чертежа посторонними линиями, от такого обозначения вспомогательных плоскостей следует отказаться и приучить учащихся воображать их.
Для закрепления решения этой задачи можно предложить следующую систему задач:
Точки А1 и В1 расположены на боковых ребрах куба ABCDA1 B1C1D1. Найти точку пересечения прямой (АВ) с плоскостью верхнего и нижнего основания.
Точки А1 и В1 расположены на смежных боковых гранях куба ABCDA1 B1C1D1. Найти точку пересечения прямой (АВ) с плоскостью нижнего основания.
Точки А1 и В1 расположены на двух смежных ребрах пирамиды ABCD. Найти точку пересечения прямой (АВ) с основанием пирамиды.
Даны тетраэдр ABCD и точки M и N, принадлежащие боковым граням. Постройте точку пересечения прямой MN с плоскостью ABC.
Точки Н и К расположены на соответственно на ребрах АВ и АD призмы ABCDA1B1C1D1. найти точку пересечения прямой (HF) с прямой (DC);(DD1).
Точки A1 и B1 расположены соответственно на ребрах АС и АВ пирамиды ABCD.Найти точку пересечения прямой (A1B1) с прямой (ВС).
Дана пирамида ABCDS.Найти точку пересечения прямой (AS) с прямой (ВК), где К-точка принадлежащая ребру CS.
Дана пирамида ABCDS. Найти точку пересечения прямой (АВ) с прямой (DH), где H-середина ребра BC.
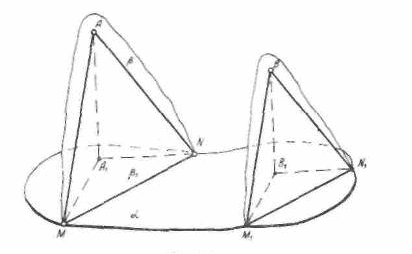
Задача: Построить линию пересечения заданных проектирующих плоскостей
Рис. 6а
Пусть проектирующие плоскости заданы проектирующими прямыми АА1 и ВВ1 ТТ1 и РР1. Одной точкой линии пересечения заданных плоскостей будет точка Х1 —точка пересечения следов обеих плоскостей. В оригинале линия пересечения проектирующих плоскостей будет проектирующей прямой, как линия пересечения двух плоскостей, проведенных через параллельные (проектирующие) прямые. Следовательно, и на изображении прямая ХХ1, по которой пересекаются проектирующие плоскости, будет параллельна АА1.
Как решение этой задачи, так и всех остальных следует рассматривать через возможно большую совокупность частных случаев. Проектирующие прямые, определяющие проектирующие плоскости, могут располагаться так, что линия пересечения плоскостей будет находиться либо между одной из пар проектирующих прямых, либо между обеими парами. Проектирующие плоскости следует задавать не только одной парой проектирующих прямых, но и проектирующей прямой и точкой, лежащей в основной плоскости.
Во всех случаях решения следует связывать с построениями в оригинале. Если, например, проектирующую плоскость рассматривать как частокол с плотно примыкающими друг к другу кольями, то учащиеся должны понимать, что линия пересечения будет колом, который находится одновременно и в первой и во второй изгородях. Линию пересечения проектирующих плоскостей можно рассматривать как стык двух листов фанеры, являющихся образами проектирующих плоскостей.
Задача: Построить линию пересечения двух произвольно заданных плоскостей
Решение задачи в соответствии с выставленными принципами, понимание которых учащимся к этому моменту должно быть.подготовлено, не должно уже вызывать затруднений..В одной из заданных плоскостей (рис.5), например в плоскости φ(φ1), берутся две произвольные вспомогательные прямые а(а) и в(в) и строятся точки — точки Х(Х1) и Y(Y1) — пересечения этих прямых с плоскостью β(β1). Прямая XY(X1Y1)— искомая.
Рис. 5
В повседневной практике в качестве вспомогательных прямых выбирают те, которые имеются уже на чертеже: следы плоскостей, прямые, определяемые точками, задающими плоскость. Одна точка линии пересечения плоскостей, заданных на рис. 6, определяется как точка пересечения следов плоскостей — точка Х(Х1). В качестве второй вспомогательной прямой а(а,) взята прямая, лежащая в проектирующей плоскости РP1 ТT1.
Рис. 6
Для закрепления решения этой задачи можно предложить следующую систему задач:
Плоскость задана тремя точками, расположенными на смежных боковых ребрах пирамиды (призмы). Найти линию пересечения этой плоскости с плоскостью нижнего основания.
Плоскость задана тремя точками, расположенными на не смежных боковых ребрах пирамиды, в основании которой лежит четырехугольник. Найти линию пересечения этой плоскости с плоскостью нижнего основания.
Плоскость задана тремя точками, две из них расположены на смежных боковых ребрах пирамиды, а третья – на боковой грани пирамиды. Найти линию пересечения этой плоскости с плоскостью нижнего основания.
Дана четырехугольная пирамида SABCD. Построить линию пересечения двух ее граней ASB и CSD
Дана четырехугольная призма ABCDABCD. Найти линию пересечения плоскости, заданной точками В,К,L, где В-вершина основания, точка K принадлежит ребру DD1,точка L принадлежит ребру CC1,с плоскостью A1B1C1D1.
Точки О и О1 являются точками пересечения диагоналей оснований куба. Найти линии пересечения плоскости, заданной точками О, О1,С с боковыми гранями.
Дано SABCD - пирамида. Точка Н- середина DC. Найти линию пересечения плоскости, заданной точками A,H,S,с плоскостью SBC.
Но для полноценного решения задач на построении полезно на основании двух опорных задач (нахождении точки пересечения с плоскостью и линии пересечения плоскостей) рассмотреть задачи.
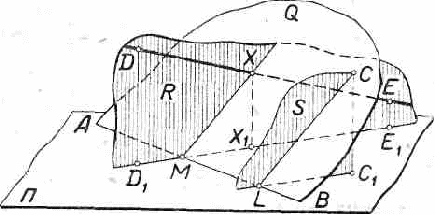
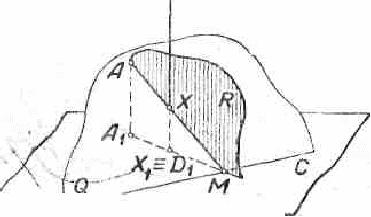
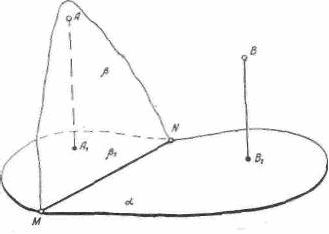
Задача 1. Найти точку пересечения плоскости Q, заданной следом ВС и точкой А(А1), с проектирующей прямой DD1 (рис. 7а).
Проводим плоскость R через точку А(А1) и данную прямую DD1 и на линии AM пересечения плоскостей Q и R находим искомую точку Х(Х1).
Рис 7а
Задача 2. Построить точку пересечения треугольника ABC(A1B1C1) с прямой DE (D1E1)
Рис 7б
Находим линию LM пересечения плоскости треугольника ABC с проектирующей плоскостью R, проходящей через данную прямую DE.
В пересечении прямых LМ и DE, лежащих в одной плоскости R, находим искомую точку X, которая на чертеже определяется своим изображением и изображением своей проекции Х1 на плоскость П.
Задача 3. Определить точку пересечения плоскости Q, заданной следом АВ и точкой С, с прямой DE (рис 7в).
Через точку С, принадлежащую плоскости Q, проводим вспомогательную плоскость S, параллельную проектирующей плоскости R, проходящей через данную прямую DE(LC1 || D1E1). Затем находим линию LC пересечения плоскости S с плоскостью Q. Далее строим прямую MX пересечения плоскостей О и R(MX || LC).
Точка X есть искомая точка пересечения, так как она одновременно принадлежит плоскости Q и прямой DE.
Рис 7в
Решением задачи заканчивается обоснование принципов построения прямых, по которым пересекаются плоскости, и точек пересечения прямых и плоскостей. Однако в классе следует решить еще несколько задач, решение которых сводится к построению точек и линий пересечения прямых и плоскостей.
Итак, при изучении задач на построение на проекционном чертеже учащиеся должны знать, что:
Точку пространства считают заданной на проекционном чертеже, если заданы изображение этой точки и изображение се проекции на основную плоскость.
Прямую считают заданной на проекционном чертеже, если заданы две ее точки или если заданы ее изображение и изображение ее проекции на основную плоскость.
Плоскость считается заданной на проекционном чертеже, если заданы три точки этой плоскости, не лежащие на одной прямой, или прямая и точка вне ее, или две пересекающиеся прямые, или две параллельные прямые.
Если все точки, прямые и плоскости изображенной фигуры являются заданными на проекционном чертеже в указанном смысле, то такое изображение называется полным и можно на нем построением отыскать все непустые пересечения прямых и плоскостей изображенной фигуры, т. е. решать различные позиционные задачи.
Решение задач на построение сечений
Работа по ознакомлению учащихся с проекционным чертежом может быть продолжена при обучении решению задач на построение сечений многогранников.
Обучение решению задач на построение сечений можно проводить в следующем плане.
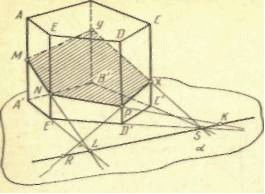
Во-первых, первоначальное ознакомление учащихся с методами построения сечений следует проводить на метрически определенных изображениях. Удобно, например, это проделать на изображении куба и правильного тетраэдра, сопровождая построения на изображении демонстрацией соответствующих отношений на модели. Все это будет способствовать укреплению связи изображения и оригинала.
Во-вторых, точки, определяющие секущую плоскость, следует задавать по возможности при разнообразном взаимном расположении этих точек и многогранника, сечение которого строится.
Рис. 7
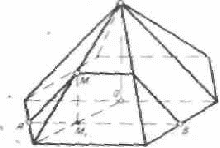
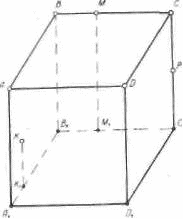
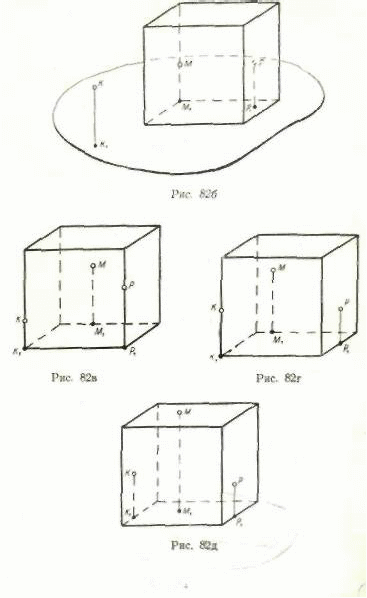
На рис.8 Приведена последовательность первых таких задач. Секущая плоскость на этих чертежах задается точками К(К1), М(М1) и Р(Р).
Рис. 8
При обучении решению как этих задач, так и любой из последующих учащимся следует выделять отдельные этапы решения, представляющие собой известные уже учащимся задачи на проекционном чертеже.
Рис. 9а
Рис. 9 б
Для построения сечения куба, представленного на рис. 9а, достаточно, например, найти точку пересечения ребра СС1 с плоскостью КМР (К1М1 Р1). Метод построения этой точки удобно раскрыть учащимся на примере решения уже известной им задачи: на проекционном чертеже (рис. 9б) построить точку пересечения плоскости β(β1)и проектирующей прямой СС1 На вспомогательном чертеже следует лишь по возможности точно воспроизвести взаимное расположение точек К(К1), M(M1), P(P1) и прямой СС1.
В порядке обеспечения преемственности в решении задач на проекционном чертеже важно подчеркнуть мысль, что в качестве вспомогательной плоскости СС1КК1 могла бы быть принята произвольная плоскость, проведенная через ребро СС1. Вместе с тем учащихся сразу следует приучать к рациональному выбору вспомогательных плоскостей.
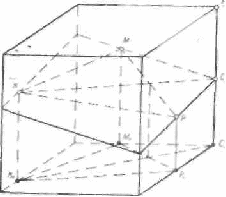
При построении сечения куба (рис. 10а) плоскостью КМР (К1М1Р1) не следует препятствовать применению общего метода (рис. 10б). Однако решение этой задачи следует вести до тех пор, пока учащиеся не догадаются, что наиболее подходящей вспомогательной плоскостью будет плоскость грани BB1 CC, (рис. 10в), а не плоскости ВВ1ЕЕ1.
рис. 10а
Рис. 10б рис. 10в
Рис. 11
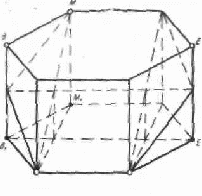
В то же время для построения сечения правильной шестиугольной призмы, высота которой равна стороне основания, плоскостью КМР (K1M1P1) удобнее принять в качестве вспомогательной плоскость ВВ1ЕЕ1 (рис. 11). В этом случае с помощью одной вспомогательной плоскости одновременно строятся точки пересечения секущей плоскости с двумя ребрами призмы.
Такой подход к решению задач на построение сечений дает надежное общее средство решения этих задач и позволяет развивать изобретательность учащихся при отыскании частных приемов.
Важный момент обучения решению задач на построение сечений при рассматриваемой методике составляет выделение в условии задач элементов, задающих секущую плоскость. Если условием задачи секущая плоскость задана точкой и прямой, или пересекающимися прямыми, или параллельными прямыми, то, выбирая на них три точки, сводим решение задачи к построению сечения плоскостью, заданной тремя точками.
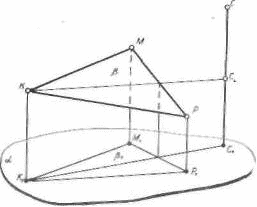
При построении сечения правильной шестиугольной призмы плоскостью, проходящей через сторону верхнего основания и образующей с основанием данный двугранный угол, прежде всего определяется пара пересекающихся прямых, задающих эту плоскость.
Секущая плоскость определяется парой пересекающихся прямых АВ и ММ (рис. 12) и при построении сечения правильной шестиугольной пирамиды плоскостью, проходящей через данную точку М1 основания пирамиды, параллельно одной из больших диагоналей основания и параллельно высоте пирамиды.
Рис. 12
Выделение секущей плоскости — один из важных этапов решения задач на построение сечений.
При решении задач на построение сечений в доходчивой форме удается познакомить учащихся с понятиями полного и метрически определенного изображений, с решением позиционных и метрических задач.
Изображение многогранников вводится как метрически определенное в соответствии с вышеизложенной методикой обучения построению изображений. К понятию полного изображения можно подвести учащихся, если добиться от них понимания, что изображение, построенное по наперед заданному оригиналу, есть в то же время изображение более широкого класса фигур. Учащиеся должны понимать, что изображение, например, правильного тетраэдра является вместе с тем и изображением всех треугольных пирамид. Изображение правильной четырехугольной призмы, высота которой в два раза больше стороны основания, является в то же время и изображением четырехугольных призм, в основании которых, лежит не только квадрат и высота которых не только в два раза больше стороны основания, изображением не только прямых призм, но и наклонных.
Навык в построении сечений целесообразнее вырабатывать на полных изображениях, не связывая себя без необходимости с оригиналами наперед заданной формы. Это тем более полезно, что на полных изображениях раскрываются и некоторые общие свойства многогранников.
Полезно, например, не только построить сечение правильной треугольной призмы (рис 13) секущей плоскостью А102С1, где 02— середина оси призмы, но и доказать, что плоскость пересечет верхнее и нижнее основания любой из правильных треугольных призм..
Рис. 13
Для построения сечения достаточно найти точку (X) пересечения ребра ВВ1, с прямой О102, по которой пересекаются вспомогательная плоскость BВ1DO1 с секущей плоскостью. Отрезок XB1=30102, так как D1B1 =3D1O1, и, следовательно, D1O2 пересечет верхнее основание.
Широкие возможности для проведения такой работы представляет построение изображений к задачам с буквенными данными.
Приведем в качестве примера решение задачи на построение сечения призмы плоскостью.
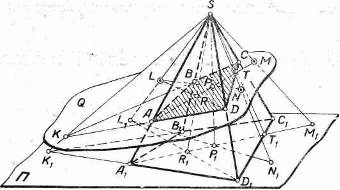
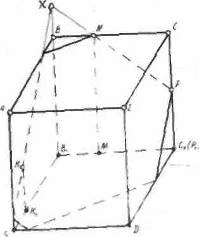
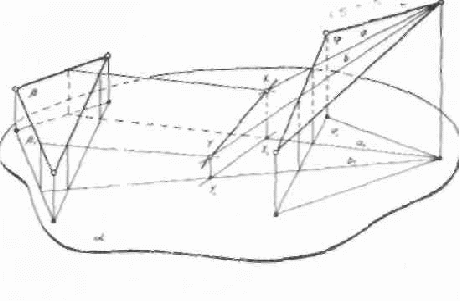
Задача. Построить сечение пятиугольной призмы плоскостью, заданной тремя точками, лежащими на боковых ребрах призмы.
Пусть дана призма ABCDEA'B'C'D'E' и три точки М, N, Р, лежащие соответственно на ребрах АА', ЕЕ', DD', (рис).
Выберем плоскость А'В'С нижнего основания за основную плоскость а, а направление боковых ребер — за направление проектирования на основную плоскость. При таком выборе основной плоскости и направления проектирования изображение призмы является полным, т. е. все элементы призмы (грани, ребра и вершины) заданы на чертеже, что легко проверить. Так как изображение является полным, то требуемое в задаче построение осуществимо на чертеже.
Задача построения сечения сводится в нашем случае к отысканию точек пересечения плоскости MNP с боковыми ребрами (проектирующими прямыми) ВВ' и СС.
Приведем символическую запись хода решения задачи
(L С MN, α) и (К С NP, α) (MNP ∩ α = KL);
R С C'D', KL;
(R С C D') и (CD' С С CD) => (R С С CD);
(R С KL) и (KL MNP)=>(R С MNP);
(P С MNP, С CD) и (R С MNP, C'CD)=>(MNP ∩C'CD=
= PR);
(X С C'C, PR) (X = MNP ∩ C C);
S С B'C, KL;
(S С B'C) и (B'C B'BC) => (S С B'BC);
(S С KL) и (KL С MNP)=>(S С MNP);
10) (XMNP,B'BC)и(SСMNP,B'BC)=>(XS=MNP∩B'BC);
11) (Y С XS, B'B)=>(Y С MNP, B'B).
Итак, MNPXY — искомое сечение.
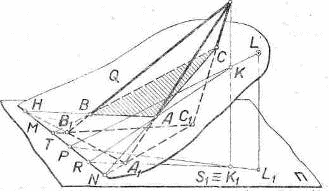
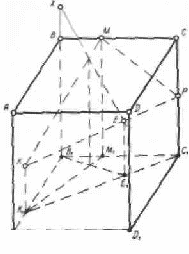
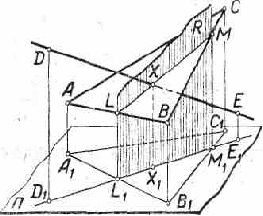
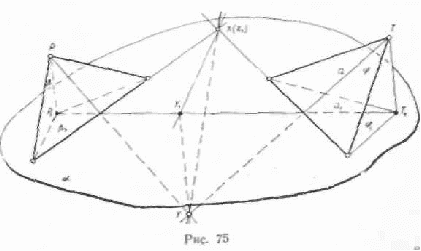
Задача 2. Найти линию пересечения четырёхугольной пирамиды SA1B1C1D1 с плоскостью Q, проходящей через точки L(L1), М (М1) и N(N1) (рис.15).
Рис 15.
Так как точки L, М и N заданы на чертеже своими изображениями и изображениями своих внутренних центральных проекций, то в данном случае целесообразно воспользоваться центральным проектированием на плоскость П из точки S, как из центра, и определять точки пересечения рёбер пирамиды с плоскостью Q. Рёбра пирамиды здесь тоже можно рассматривать как проектирующие прямые.
Соединим точки L1 с N1, L с N и А1 с М1, затем через
точкуРх=L1N1∩A1M1 проведём проектирующую прямую SP1 и найдём точку Р=LN∩SP1. Далее,прямую MP продолжим до пересечения в точке А с ребром SA. Точка А есть точка пересечения ребра SA1 с плоскостью Q.
Черт. 51.
Чтобы найти точку D пересечения ребра SD1 с плоскостью Q, через точку R1 =A1M1∩L1D1 проведём проектирующую прямую SR1, пересекающую прямую AM в точке R, и прямую LR продолжим до пересечения с ребром SD1.
Аналогично можно найти точки В и С. Но мы здесь для определения точки С использовали точку Т=АМ ∩ ST1 и для построения точки В нашли линию SK1 пересечения граней SA1D1 и SB1C1, а точку К= SK1 ∩ AD соединили с точкой С. Отметим, что эти приёмы могут быть использованы при проверке построений. Линия ABCD есть искомая линия пересечения данной пирамиды с плоскостью.
Используемая литература
1. А.Р. Зенгин «Основные принципы построения изображений в стериометрии». Государственное учебно- педагогическое издательство Министерства Просвещения РСФСР. М. 1956.
2. А.Д. Семушкин «Методика обучения решению задач на построение по стереометрии».Издательство академии педагогических наук РСФСР. М. 1959
3. А.А. Столяр «Педагогика математики». Издательство «Высшая школа» 1986.

Нравится материал? Поддержи автора!
Ещё документы из категории педагогика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ