Обобщения при обучении решению математических задач

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Вятский государственный гуманитарный университет»

Физико-математический факультет

Кафедра дидактики физики и математики

Выпускная квалификационная работа

Обобщения при обучении решению математических задач

Киров

2008

Оглавление

Введение

1. Теоретические основы обобщений при обучении школьников математике

1.1. Понятие обобщения и его роль при обучении математике

1.2. Виды и приемы обобщений

1.3. Сравнение и анализ – необходимые условия обобщения

1.4. Обобщения по аналогии при обучении решению задач

1.5. Индуктивные обобщения при обучении решению задач

Выводы по первой главе

2. Методические рекомендации осуществления обобщений на уроках математики при обучении решению задач

2.1. Обобщения при обучении методам решения математических задач

2.1.1 Обобщение способов решения конкретных задач до метода решения класса задач

2.1.2 Обобщение методов решения задач

2.1.3 Обобщение способов поиска решения многих задач до системы советов

2.2 Обобщение как метод решения математических задач

2.2.1 Обобщение решений задач по индукции

2.2.2 Решение задач «в общем виде»

2.3 Обобщение как источник новых математических задач

2.3.1 Обобщение данных при сохранении искомых

2.3.2 Обобщение (добавление искомых) при сохранении данных

2.3.3 Обобщение данных и искомых

2.4 Обобщения задач ведущие к формированию математических понятий и теорем

2.5 Таблицы как средство обобщения при обучении решению математических задач

2.6 Опытное преподавание

Выводы по второй главе

Заключение

Библиографический список

Введение

Во все времена отмечалась большая значимость математического образования для человека. В процессе усвоения математических знаний происходит развитие навыков проведения логических рассуждений, овладение умениями анализировать, обобщать, специализировать, определять понятия, составлять суждения, находить пути решения поставленной задачи. При изучении математики формируется мышление учащихся, развивается речь, а так же такие качества выражения мысли, как порядок, точность, ясность, краткость, обоснованность.

Основной задачей методики преподавания математики является поиск путей повышения эффективности процесса обучения школьников математике.

По мнению ученых решению проблемы способствует использование обобщений в процессе обучения. Изучением вопроса осуществления обобщений на уроках математики занимались многие методисты – математики В.Г. Болтянский, В.А. Далингер, Е.С. Канин, Г.И. Саранцев, А.А. Столяр, Д. Пойа, Р.С. Черкасов и другие.

В школьной же практике обобщения используются чаще при изучении понятий, реже теорем, и совсем редко при обучении решению задач.

По мнению учителей математики, главной причиной недостаточного осуществления обобщений на уроках решения задач является отсутствие методических рекомендаций. Поэтому необходимо разработать такие рекомендации по осуществлению обобщений в процессе обучения решению математических задач. Это определяет актуальность данной работы.

Объектом исследования является процесс обучения решению задач на уроках математики в средней (полной) школе.

Предмет исследования – обобщения при обучении решению математических задач.

Цель работы: рассмотреть теоретические основы обобщений при обучении школьников математике, разработать методические рекомендации (содержательный аспект) осуществления обобщений при обучении решению математических задач и опробировать их на уроках математики в 10м классе.

Гипотеза исследования: если на уроках математики организовать процесс обучения решению задач в соответствии с предложенными методическими рекомендациями, то это позволит повысить результативность обучения школьников решению задач.

Для достижения поставленной цели необходимо решить следующие задачи:

Рассмотреть понятие обобщения, виды и приемы обобщений в философской, психолого-педагогической, математико-методической литературе и их роль в процессе обучения математике.
Выявить необходимые условия осуществления обобщений при обучении математике.
Рассмотреть обобщения по аналогии и индуктивные обобщения при обучении решению математических задач.
Разработать методические рекомендации осуществления обобщений при обучении учащихся средней (полной) школы решению математических задач и проверить их эффективность в 10 классе.

Методы исследования:

Для решения поставленых задач использовались следующие методы: изучение философской, психолого-педагогической, математико-методической литературы по проблеме осуществления обобщений в процессе обучения математике, наблюдение за работой учителей математики в период практики, применение разработаных учебно – методических материалов в процессе обучения математике.

Работа состоит из введения, двух глав, заключения и библиографического списка.

Практическая значимость работы состоит в том, что разработанные методические рекомендации могут быть использованы учителями математики в их деятельности.

1. Теоретические основы обобщений при обучении школьников математике

1.1. Понятие обобщения и его роль при обучении математике

Проблеме обобщения в процессе познания посвящены труды многих ученых философов, психологов, педагогов, математиков.

С точки зрения логики обобщение – это «построение (выведение) универсальных и экзистенциальных утверждений: а) в системах дедуктивной логики – на основе постулируемых правил построения таких утверждений (правил вывода для кванторов общности и существования) – т. н. обобщение переменных; б) в системах индуктивной логики на основе опытных (экспериментальных) данных («данных эмпирических свидетельств») – т.н. индуктивные обобщения». С гносеологической (и методологической) точки зрения обобщение – это «одно из важнейших средств научного познания, процедура перехода на более высокий уровень абстракции на основе выявления (в рассматриваемой области предметов) общих для этих предметов признаков: свойств, отношений, тенденций развития и т.п.» [40].

В философском энциклопедическом словаре обобщение понимается как «мыслительный переход: 1. От отдельных актов, событий к отождествлению их в мыслях (Предмет -> Мысль). 2. От одной мысли к другой (Мысль -> Мысль)» [41].

Д.П. Горский понимает под обобщением мыслительную операцию, переход от мысли об индивидуальном, к мысли об общем, от мысли об общем к мыслям о более общем; а так же переход от отдельных фактов, предметов и явлений к отождествлению их в мыслях и образованию о них общих понятий и суждений [8].

В психолого-педагогической литературе также имеются различные подходы к определению понятия «обобщение». В трактовках понятия прослеживается связь обобщения и мышления, обобщения и познания.

С.Л. Рубинштейн говоря о мышлении, утверждает, что «всякое мышление совершается в обобщениях. Оно всегда идет от единичного к общему и от общего к единичному. Мышление – это движение мысли, раскрывающее связь, которая ведет от отдельного к общему и от общего к отдельному. Мышление – это опосредованное – основанное на раскрытии связей, отношений, опосредовании – и обобщенное познание объективной реальности» [37, с. 310]. Автор отмечает, что обобщение можно понимать как основной путь образования понятий. В процессе обобщения происходит, с одной стороны, поиск и обозначение словом некоторого инварианта в многообразии предметов, с другой – опознание предметов данного многообразия.

Л.С. Выготский в своей психологической теории трактует обобщение как особый способ отражения действительности в сознании человека [7].

В психологическом словаре под редакцией В.В. Давыдова дается следующее определение обобщения: «Обобщение – одна из основных характеристик познавательных процессов, состоящая в выделении и фиксации относительно устойчивых, инвариантных свойств предметов и их отношений» [34].

Педагоги понятие «обобщение» также определяют неоднозначно.

В педагогическом энциклопедическом словаре обобщение определяется как «переход на более высокую ступень абстракции путем выявления общих признаков (свойств, отношений, тенденций развития и т.п.) предметов рассматриваемой области; влечет за собой появление новых научных понятий, законов, теорий. Обобщение обеспечивает мышлению учащихся определенность и последовательность» [29].

«Осмысление непосредственно перерастает в процесс обобщения знаний, в ходе которого обобщаются и объединяются общие существенные черты предметов и явлений действительности, изучаемых в соответствующий период обучения» – утверждает Ю.К. Бабанский [28, с. 147]. По его мнению, обобщение является одним из структурных этапов усвоения знания (восприятие, понимание, осмысление, обобщение, закрепление, применение).

При обучении математике распространенным является определение обобщения через множества. Д. Пойя [30] и Ю.М. Колягин [23] определяют обобщение как переход от данного множества предметов к рассмотрению более «емкого» множества, содержащего данное.

В пособиях по методике преподавания математики распространено понятие обобщения как операции мысленного выделения каких-либо общих существенных свойств, принадлежащих только данному классу предметов или отношений [22].

Обобщение как переход от понятий и теорем к более общим раскрывают М.С. Бернштейн [4], К.С. Богушевский [5], Д.И. Розенфельд [36], А.Г. Мордкович [26] и другие.

Как переход от ключевых, опорных задач к более сложным рассматривают обобщение Я.П. Понарин [33], Р.Г. Хазанкин [12] и другие.

Обобщение как инструмент при составлении моделей определяется в работах Л.М. Фридмана [42], П.М. Эрдниева [43] и других.

Обобщение способов решения задач рассматривают А.И. Островский [27], Е.С. Канин [14], Г.В. Дорофеев [11] и другие.

Обобщение как прием систематизации математических знаний и умений рассматривает в своих работах В.А. Далингер [21].

Как эффективный эвристический прием открытия новых фактов рассматривает обобщение Г.И. Саранцев [38] в своей книге «Общая методика преподавания математики». Он считает, что обобщение, как форма перехода от частного к общему, имеет целью выделение общих существенных свойств, принадлежащих определенному классу объектов.

Не смотря на различные подходы к определению понятия «обобщение», все ученые признают важную роль обобщений в процессе познания:

образование любого общего понятия действительности необходимым образом включает процесс обобщения;
обобщения дают возможность раскрывать внутренние связи между различными уже открытыми законами; благодаря обобщениям создаются эффективные единые правила оперирования с изучаемыми предметами;
обобщенные теории дают возможность объяснять факты, которые не могли быть объяснены в пределах прежней теории.
обобщение развивает мотивацию к обучению, облегчает изучение и применение знаний учащимися, улучшает качество знаний, что в итоге приводит к повышению образовательного, воспитательного и развивающего потенциала обучения.

Необходимость осуществления обобщений в обучении математике отмечают В.Г. Болтянский [6], Ю.М. Колягин [23], Д. Пойа [30], Г.И. Саранцев [38] и другие. Они считают, что знания, за которыми не стоит обобщающей работы мысли, – это формальные знания.

П.М. Эрдниев видит значение обобщения в том, что его применение в процессе обучения помогает самостоятельному расширению и углублению имеющихся знаний, так как «обобщение связано с преобразованием мыслей, с умственным экспериментированием; с развитием интуиции и перебором различных образов при отыскании общего знания. Обобщение есть одно из самых важных средств самообучения, автодидактики». Он также отмечает, что умение обобщать является непременной составной частью творческого мышления, так как «этим путем мысль человека выходит за пределы известного, пролагая путь к неизвестному» [43, c. 61].

С помощью обобщения происходит развитие творческих способностей учащихся; развитие познавательного интереса при решении задач [39], формирование и развитие умения сравнивать, что имеет большое значение в развитии мышления учащихся [16]; формирование умения видеть за абстрактными обозначениями реальные взаимосвязи в задачах [19].

Задачи являются и целью, и средством обучения математике. Поэтому необходимо использовать потенциал обобщения в процессе обучения решению задач, так как обобщения могут способствовать выводу общего метода решения некоторого класса задач из решений конкретных задач, выступать как метод решения задач, например, обобщенная задача может оказаться легче и понятнее исходной. При составлении новых задач обобщение является средством видоизменения задачи.

Таким образом, в работе под обобщением будем понимать переход от единичного к общему, от менее общего к более общему за счёт выделения общих существенных свойств или отношений. Обобщение играет очень важную роль в процессе обучения математике. С помощью обобщения происходит расширение и углубление знаний, а так же их систематизация. Обобщение помогает в формировании и развитии мотивации к изучению математики. Оно способствует усилению внутрипредметных связей, развивает творческое мышление и познавательный интерес в процессе обучения, является существенной стороной мыслительной деятельности. Необходимо использовать потенциал обобщения в процессе обучения решению математических задач. При решении задач обобщение может осуществляется как метод решения, или, наоборот, помочь в выводе метода решения задачи, а так же удобно при составлении новых задач.

1.2 Виды и приемы обобщений

В методике преподавания математики нет общепринятой классификации видов обобщения. Используя обобщения, методисты в основном берут за основу классификации философов и психологов.

Наиболее распространенной является классификация способов обобщений, предложенная Д.П. Горским [9].

1. Обобщение посредством перехода от конкретных высказываний к предложениям, содержащим переменные. (Введение понятия многоугольника, многогранника, уравнения и др. математические понятия после рассмотрения отдельных примеров.)

2. Обобщение посредством введения новых понятий, правил, операций, законов. (Введение понятий конгруэнтности, равновеликости, равнонаправленности, подобия фигур, понятий симметрии и др.)

3. Обобщение посредством анализа смысла некоторых выражений, возникающих в ходе развития науки. (В арифметике – введенное Эйлером определение умножения целого числа на дробь через обращение к закону коммутативности, в геометрии – введение понятия угла между скрещивающимися прямыми, между прямой и плоскостью, понятий двугранного, многогранного угла и др.)

4. Обобщение как перенесение закономерностей, действительных для одной области, на новые предметные области. (Величины и числа, алгебраизация геометрии и др.)

5. Обобщение посредством индукции, т.е. переход от суждений, теорий, имеющих частное значение, к общим закономерностям. (В арифметике: всякое четное число можно представить в виде суммы двух простых чисел; в геометрии: все рассматриваемые в пространстве фигуры, обладающие свойством симметрии, имеют либо бесконечное, либо конечное нечетное число осей симметрии и др.)

6. Обобщение с помощью объединения двух или нескольких закономерностей в одну более общую закономерность. (Понятие о геометрических преобразованиях, композиции преобразований и др.).

Деление обобщений на эмпирические и теоретические, осуществленное С.Л. Рубинштейном и В.В. Давыдовым, так же используется в методике преподавания математики.

В основе эмпирического обобщения лежит операция сравнения. Проводя сравнение одной группы предметов, ученик выделяет их внешние, одинаковые общие свойства, обозначает их каким-либо словом, которое в результате может стать понятием об этой группе предметов.

Теоретическое обобщение осуществляется путем анализа данных о каком-либо одном предмете с целью выделения существенных внутренних связей, которые определяют этот предмет как целостную систему.

С.Л. Рубинштейн [37] выделил две характерные черты теоретического обобщения:

1) оно выполняется при таком анализе какого-либо одного конкретного факта (события, задачи), который обнаруживает внутреннюю связь его частных проявлений;

2) исходя из знания этой связи, ученик затем сразу может обобщить все другие факты (события, задачи) данного круга.

Если для эмпирического обобщения характерно длительное сравнение многих исходных фактов для их постепенного обобщения, то для теоретического обобщения этого не требуется. Теоретическое обобщение строится на рефлексии, которая состоит в рассмотрении учащимися оснований собственных действий и их соответствия условиям задачи, и на анализе содержания задачи с целью выделения принципа или всеобщего способа ее решения.

В качестве приемов обобщения при обучении решению задач ученые выделяют отбрасывание ограничений, введение параметра, видоизменение задачи, построение «теории в малом масштабе» и т.д.

Г.И. Саранцев считает, что «использование обобщения при решении задач основано на расширении области изменения параметра, или на переходе от данного множества к более широкому множеству, содержащему данное. Первое направление преимущественно применяется в алгебре, второе – в геометрии» [38, с. 110]

В качестве приема отбрасывания ограничений, можно рассматривать обобщения данных или искомых задачи в различных проявлениях:

1) отбрасывание ограничений путем замены числовых данных или искомых параметром;

2) отбрасывание ограничений путем обобщения понятий, входящих в содержание задачи;

3) отбрасывание ограничений на требования задачи, постановка более общего вопроса;

4) отбрасывание ограничений путем введения большего числа элементов задачи;

5) отбрасывание ограничений на применимость (решение конкретной задачи применяется для целого класса задач).

Этот прием широко используется при обучении решению математических задач.

При обобщении сами математические задачи можно объединить в некоторые множества. Например, задачи, приводимые к формированию математического понятия; задачи, приводящие к теореме; задачи, приводящие к методу решения класса задач и другие. От данного множества задач осуществляется переход к более широкому множеству, содержащее данное.

Таким образом, нет общепринятой классификации видов обобщения. В методике преподавания математики в основном используются классификации педагогов и психологов. Основными приемами обобщения при решении математических задач являются отбрасывание ограничений и переход от данного множества задач к более широкому, содержащее данное.

1.3 Сравнение и анализ – необходимые условия обобщения

Обязательным условием всякого обобщения является сравнение. Как уже было отмечено, сравнение является основой эмпирических обобщений. П.М. Эрдниев [43] при обучении математике на основе теории укрупнения дидактических единиц придает большое значение основным формам сравнения: сопоставлению и противопоставлению.

Анализ же является основой теоретических обобщений.

По мнению В.Г. Болтянского «анализ представляет собой наиболее трудную, творческую стадию процесса решения задачи» [6, с. 35]. Именно в умении анализировать условие задачи, поиск решения, само решение, полученный результат проявляется обобщенность подхода к решению задач.

«Обобщение через анализ является мощным средством для выявления существенных для решения данной задачи свойств путем формирования теоретического мышления» считает Ю.М. Колягин [23, с. 53]. Это справедливо, так как, по мнению психологов, неотъемлемым признаком теоретического мышления является способность к анализу задачи, который вскрывает внутреннюю связь, лежащую в основе многих частных проявлений этой задачи.

Часто учащиеся выясняют метод решения задач определенного класса на основе анализа одной-двух задач. При этом способные к математике школьники значительную часть времени затрачивают не столько на анализ условия задачи, сколько на анализ требования. Благодаря такому анализу они могут решать одну и ту же задачу разными способами. Переход от одного способа к другому, свободная ориентация в материале, свидетельствуют о его обобщенности.

«Анализ при решении задачи включает в себя несколько составляющих: составно-структурную, функциональную, генетическую, которые раскрываются в определенной последовательности». [20, с. 61] Составно-структурная составляющая анализа предполагает ответы на вопросы: из каких элементов, подзадач, блоков образована задача? Что они собой представляют? Оптимален ли набор элементов? Эта составляющая заключается в том, чтобы выяснить внутреннюю структуру, организацию задачи как системы, определить способ, характер связей и отношений элементов ее составляющих. Функциональная – в раскрытии механизма внутреннего функционирования задачной системы. Генетическая – в исследовании происхождения задачи, процесса ее формирования и развития.

Весьма важной при проведении обобщений является генетическая составляющая анализа. Ведь гораздо легче воспринять знание, проследив его возникновение, нежели чем когда оно дано как факт.

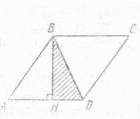
Пример1. задачу на вычисление площади треугольника подобного данному с известной площадью, если известен коэффициент подобия можно обобщить до класса задач на вычисление площади многоугольника подобного данному с известной площадью, если известен коэффициент подобия. При этом используется формула отношения площадей подобных треугольников: 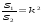. Тогда, анализируя задачу, когда S₁ и S₂ – площади треугольников, можно сделать обобщение, когда S₁ и S₂ – площади многоугольников. Это обобщение, в свою очередь, может быть рассмотрено для конкретных многоугольников.

Составно-структурная составляющая проявляется в анализе структуры задачи и ее решения.

При помощи функциональной составляющей анализа можно выделять общее не только в задачах и их решениях, но и в мыслительной деятельности при решении задач. Д. Пойа в работе «Как решать задачу» [30] разработал методику решения задач по математике, представив ее в виде таблицы советов решающему математическую задачу. Советы носят организационно-эвристический характер, направленный на оптимальное стимулирование мышления к достижению поставленной в задаче цели.

Таким образом, сравнение и анализ являются обязательными условиями всякого обобщения. Эффективность осуществления обобщений зависит от умения проводить анализ задачи. При проведении анализа задачи, выявляется общее как в задачах и их решениях, так и в мыслительной деятельности.

1.4 Обобщения по аналогии при обучении решению задач

«Случаи, в которых применима аналогия, неисчерпаемы по своему разнообразию», – говорит Д. Пойа [32].

Аналогия является хорошим источником новых фактов и задач.

Д.П. Горский утверждает, что аналогия необходима для «получения нового знания, чтобы менее понятное сделать более понятным, представить абстрактное в доступной форме, конкретизировать отвлеченные идеи». Так же аналогия может служить «средством выдвижения новых гипотез, являться методом решения задач путем сведения их к ранее решенным задачам и т.п.» [8, с. 14].

Обобщения по аналогии используются для движения мысли от общности одних свойств и отношений у сравниваемых предметов к общности других свойств и отношений.

Часто аналогии скрываются в кажущихся различиях. Обнаружение таких скрытых аналогий между закономерностями, которые ранее рассматривались отдельно и не считались связными, является «одним из самых приятных моментов математического творчества» [35, с. 110]. Эвристическая ценность данного подхода заключается, в том, что происходит сближение различных, казалось бы изначально отдаленных, предметных областей математики.

Д. Пойа в книге «Математика и правдоподобные рассуждения» рассматривает использование аналогии при решении задач. Иногда можно почти копировать решение близкой, родственной задачи. В более сложных случаях аналогия может подсказать направление, в котором следует продолжать работу по решению задачи. Аналогии полезны как в понимании задачи и ее решения, так и в отыскании решения. С помощью аналогии могут быть подсказаны или сделаны более ясными общий план или значительные части решения.

Часто задачи, аналогичные по содержанию, аналогичны и по методу решения. Поэтому задачу, аналогичную по содержанию данной, легко можно решить тем же методом, а решение задачи, аналогичной данной, но более общей, может привести к открытию нового общего метода решения класса задач.

Д. Пойа предлагает следующий алгоритм, который может быть применен для решения сложных задач: для начала следует выделить аналогичную, более легкую задачу, решить ее, затем переделать ее решение так, чтобы оно могло служить в качестве модели для первоначальной задачи, и наконец, добиться решения первоначальной задачи, следуя только что созданной модели.

Рассмотрим примеры 2 и 3:

Пример 2. Зная стороны а, b, с треугольника ABC, вычислите радиус r₁ вневписанной окружности, касающейся стороны ВС и продолжений сторон АВ и АС.

Для задачи аналогичной более общей будет следующая задача:

Пример 3. Зная стороны а, b, с треугольника ABC, вычислить радиус r вписанной окружности.

Решение этой задачи рационально разбить на отдельные простейшие «шаги», после чего аналогия будет легко заметна. Решение исходной задачи (пример 2) можно получить по аналогии с решением задачи (пример 3). Для этого достаточно провести аналогию на каждом «шаге» решения [3].

В математике выделяются основные аналогии, которые часто используются при обучении решению задач: аналогии между планиметрией и стереометрией, аналогии между числами и фигурами, аналогии между бесконечным и конечным, аналогии между природой и математикой [32].

Таким образом, аналогия имеет широкое применение при обучении решению задач. С помощью аналогии осуществляется связь планиметрии и стереометрии, чисел и фигур и другие. Часто для решения сложной задачи удобно использовать решение более простой аналогичной задачи. Так же аналогия может подсказать направление, в котором следует продолжать работу по решению задачи, сделать более ясными общий план или значительные части решения. Задачу, аналогичную данной по содержанию, легко можно решить тем же методом. Решение задачи, аналогичной данной, но более общей, может привести к открытию нового общего метода решения класса задач.

1.5 Индуктивные обобщения при обучении решению задач

Индукция представляет собой метод рассуждений от частного к общему, вывод заключения из частных посылок [22]. Индуктивные обобщения играют большую роль в получении обобщенного знания и являются одним из важных эвристических приемов [3].

При отыскании математических закономерностей, при нахождении способа решения разнообразных математических задач индуктивное обобщение проявляется в умении наблюдать и выявлять общее. Метод рассуждений, где после наблюдения за серией частных случаев формулируется общее предложение, называется неполной индукцией.

Пример 4. «Доказать, что произведение трех любых последовательных натуральных чисел делится на 6» [43, с. 79].

1) Рассмотрим серию частных случаев:

1*2*3=6 (делится на 6)

2*3*4=24 (делится на 6)

3*4*5=60 (делится на 6)

2) Сформулируем предположение: числа 6, 24, 60 делятся на 6, значит произведение трех любых последовательных натуральных чисел может делиться на 6.

3) Испытаем предположение для другого частного случая: 13*14*15=2730 (=455*6 т.е. делится на 6).

Так как предположение подтвердилось, то можно сформулировать индуктивный вывод: произведение трех любых последовательных натуральных чисел делится на 6.

4) Проведем доказательство предположения: пусть k – произвольное натуральное число.

Возможны три случая:

Первое число равно 3*k, то есть кратно трем, тогда из двух последующих одно обязательно четное. Значит, произведение делится на 6.
Последнее число равно 3*k, то есть кратно трем, тогда из двух предыдущих одно обязательно четное. Значит, произведение делится на 6.
Среднее число равно 3*k.

Тогда: (3*k – 1)* 3*k *(3*k + 1) = 3*k *(9*k² – 1)

Далее возможны два случая:

k = 2*p. Предложение доказано.

k=2*p + 1.

Имеем: 3*k *(9*k² – 1) = 3*[9*(2*p +1)² – 1]*(2*p + 1)

Так как множитель в квадратных скобках – четное число, то все произведение делится на 6.

Таким образом, предложение доказано полностью: произведение трех любых последовательных натуральных чисел делится на 6.

Д. Пойа утверждает, что индуктивное обобщение может являться также методом решения математических задач [32]. Рассматривается самый простой частный случай, когда задача решается легко. Решив эту задачу, обобщают ее на другой более общий, но все же частный случай, используя в решении результат предыдущей задачи. Так доходят до общей данной задачи.

В процессе обучения математике индукция очень тесно связана с дедукцией. Особенно ярко взаимосвязь индукции и дедукции просматривается при решении задач методами полной и математической индукции.

Иногда при полной индукции результат достигается в два этапа.

1. Выделение благоприятного частного случая – особого случая, более простого, чем общий. Решение этого частного случая;

2. Объединение частных случаев, к которым применимо ограниченное решение. Получение полного решения для общего случая.

Математическая индукция применяется с целью установления истинности математической теоремы в бесконечной последовательности случаев.

Пример 5. Докажем, что для всех натуральных n истинна формула

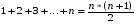
При n=1 формула верна:
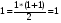
Предположим, что формула верна для n=k.
Докажем, что формула верна для n=k+1, то есть

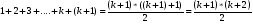
Это верно, так как

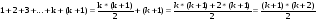
На основании принципа математической индукции сделаем вывод: формула верна для всех натуральных п.

Таким образом, индуктивные обобщения являются эвристическим приемом в обучении решению задач. Индуктивные обобщения используются в открытии математических закономерностей, при выводе метода решения задач. При решении задач индукция связана с дедукцией. Особенно это проявляется при решении задач методом полной индукции и методом математической индукции.

Вывод по первой главе.

В своей работе под обобщением будем понимать переход от единичного к общему, от менее общего к более общему за счёт выделения общих существенных свойств или отношений.

Роль обобщения при обучении решению математических задач состоит в расширении и углублении знаний, их систематизации; в формировании и развитии мотивации к изучению математики; усилении внутрипредметных связей, развитии творческого мышление и познавательного интереса в процессе обучения. Обобщение может использоваться как метод решения, как средство вывода метода решения задачи, при составлении новых задач.

В методике преподавания математики нет общепринятой классификации видов обобщений. В качестве приемов обобщений при обучении решению задач выделяют отбрасывание ограничений, введение параметра, видоизменение задачи.

Сравнение и анализ являются обязательными условиями всякого обобщения. Эффективность осуществления обобщений зависит от умения проводить анализ задачи.

Часто для решения сложной задачи удобно использовать решение более простой аналогичной задачи. Задачу, аналогичную данной по содержанию, легко можно решить тем же методом. Решение задачи, аналогичной данной, но более общей, может привести к открытию нового общего метода решения класса задач.

Индуктивные обобщения используются в открытии математических закономерностей, при выводе метода решения задач.

2. Методические рекомендации осуществления обобщений на уроках математики при обучении решению задач

Использование теоретических основ обобщений будет представлено в методических рекомендациях осуществления обобщений на уроках математики при обучении решению задач.

При обучении школьников решению задач можно выделить следующие обобщения:

Обобщения при обучении методам решения математических задач.
Обобщение как метод решения математических задач.
Обобщение как источник новых математических задач.
Обобщения задач ведущие к формированию математических понятий и теорем.

Так же необходимо выделить использование таблиц как средства обобщения при обучении решению математических задач.

2.1 Обобщение при обучении методам решения математических задач

Важную роль при обучении методам решения задач играют индуктивные обобщения. С их помощью осуществляется переход от одних методов решения задач к другим, более общим, которые можно применить к решению широкого класса задач. Также индуктивные обобщения подходов к решению задач позволяют создать систему советов эвристико – организационного характера.

В обучении методам решения математических задач можно выделить следующие индуктивные обобщения:

1) индуктивные обобщения способов решений конкретных задач до метода решения класса задач;

2) индуктивные обобщения методов решения задач;

3) обобщения и систематизации способов поиска решений многих задач до системы советов решающему математическую задачу.

Рассмотрим их подробно.

2.1.1 Обобщение способов решения конкретных задач до метода решения класса задач

Решение конкретной задачи часто может привести к методу решения класса задач. Таким образом осуществляется обобщение способа решения конкретной задачи до метода решения класса задач.

Выбирается конкретная задача, ее решение записывается в таблицу, состоящую из двух столбцов (табл. 1). В левом столбце – решение конкретной задачи, в правом – решение обобщенной задачи.

Пример 6. Найти число, 2% которого равно 12.

Табл. 1

Решение конкретной задачи

Решение обобщенной задачи

Найти число, 2% которого равны 12

Найти число, если известен процент и его значение.

1. Найдем сколько составляет один процент от числа. для этого: 12:2=6

1. Нахождение числа, которое приходится на один процент заданного числа.

2.так как все число составляет 100%, умножаем число, полученное на один процент на 100: 6*100=600

2. Умножение полученного числа на 100.

Итак, число равно 600

6. Запись ответа

Решение рассмотренной конкретной задачи приводит и к такому обобщению: для того, чтобы найти число, если известно, сколько составляет конкретное число процентов от него, нужно найти, сколько составляет один процент заданного числа, а зачем умножить это значение на 100.

Специализация метода решения задач на отыскание числа, если известен процент и его значение позволяет решать все задачи этого класса.

Пример 7. Фабрика выпускает калькуляторы партиями. Брак в каждой партии обычно бывает 9 калькуляторов, что составляет 2% от общего количества. Сколько калькуляторов в одной партии?

Так же обобщение может осуществляться путем абстрагирования от конкретных сюжетов нескольких задач и построения общей математической модели для различных по фабуле задач. Математическая модель задачи производится переводом реально происходящих в действительности процессов и явлений на язык математики и позволяет показать применение математики как инструмента для математизации реальных практических ситуаций. Таким образом, моделирование является обобщением нескольких задач и методом решения различных классов задач.

Пример 8. Клоун на ходулях хочет показать мастер – класс и обойти всю арену по краям за 5 шагов и вернуться в исходное место, при этом для красоты шаги должны быть одинаковы. Помогите клоуну, указав ему путь по арене.

Пример 9. 5 спасателей натягивают батут круглой формы для спасения человека. Как лучше спасателям держать батут, чтобы натяжение было наилучшим.

Сравнение и анализ геометрических моделей этих задач приводят к выводу: задачи, несмотря на различие формулировок, имеют одинаковые геометрические модели.

Абстрагируясь от конкретных фабул задач, формулируют обобщенную задачу: в окружность вписать правильный пятиугольник.

Понять, что для решения задачи необходимо только вписать правильный пятиугольник в окружность, мы смогли тогда, когда построили геометрическую модель задачи. Решение обобщенной задачи позволяет так же решать все задачи такого типа.

Обобщение применимо при переходе от конкретных задач к общим моделям их решения, а затем к методу решения класса аналогичных задач.

Пример 10: изучение пропорциональных зависимостей величин в 7 классе: скорость, время, расстояние (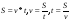); цена, количество товара, стоимость (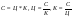); производительность труда, время работы, объем работы (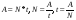). В основном, в сознании учащихся все эти задачи укладываются независимо друг от друга. В каждой задаче ее содержанию соответствует определенная группа величин, находящихся между собою в функциональной зависимости. Если абстрагироваться от конкретного содержания задач, то легко заметить, что во всех рассмотренных случаях задачные ситуации описываются с помощью двух функций: 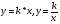. Это и есть простейшие математические модели прямой и обратной пропорциональности. Таким образом, задачи на различные прямо пропорциональные зависимости решаются с использованием модели у = к*х, а обратно пропорциональные – применением модели 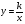» [20].

Так же распространено обобщение решения различных конкретных задач до метода решения класса задач.

Пример 11. Введение метода построения вспомогательных треугольников, который позволяет на протяжении изучения всего курса геометрии решать многие задачи на построение единым подходом, хотя они могут быть и различного содержания.

Суть метода – построение вспомогательных треугольников и использование их свойств и вновь полученных элементов для окончательного решения задачи [18].

Данные удобно представить в виде таблицы. [Приложение 8]

На анализе построение трех задач можно вывести общий метод построения всех задач такого класса, который записывается в последний столбец таблицы. При таком подходе учащиеся четко различают этапы метода.

2.1.2 Обобщение методов решения задач

При изучении методов решения математических задач индуктивные обобщения могут осуществляться следующим образом:

1) обобщение и систематизация способов решения конкретных задач до методов решения класса задач;

2) обобщение и систематизация методов решения класса задач.

Для систематизации знаний учащихся, приобретенных при решении конкретных задач, полезно делать обобщения решений до метода решения класса задач.

Пример 12: обобщение и систематизация методов решения задач о длине окружности и площади круга.

После решения ряда задач с применением формул длины окружности и площади круга в 9 классе на уроке геометрии можно провести с учащимися обобщающую беседу.

Основными при изучении темы «длина окружности и площадь круга» являются шесть объектов: R – радиус, С – длина окружности, S – площадь круга, угол с градусной мерой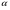, L – длина дуги, S_c – площадь сектора.

В беседе следует отметить, что формула длины дуги это обобщенный случай формулы длины окружности, то есть когда угол равен 360⁰. Аналогичное обобщение можно провести и с формулой площади круга до формулы площади сектора. Тогда количество объектов уменьшится с шести до четырех и можно рассмотреть два основных соотношения между ними:

, .

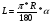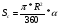Если заданы два компонента из четырех, то две оставшиеся могут быть вычислены. Таким образом, возможные типы задач определяются данными: 1) L, 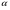; 2) S, 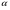, 3) R, 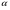, 4) L, R, 5) S, R, 6) S, L.

Если же речь идет о длине окружности и площади круга, то количество типов задач уменьшается. Целесообразно провести специализацию и рассмотреть этот случай. Обобщение показывает взаимосвязь нахождения длины окружности и длины дуги окружности, площади круга и площади сектора, так как такие громоздкие формулы плохо запоминаются учащимися.

Такие обобщения позволяют выявить связи изучаемого с изученным ранее и сформировать как общие методы решения классов задач, так и систему методов решения задач.

Индуктивные обобщения методов решений задач, а так же их систематизация приводят к формированию системы советов решающему математическую задачу.

2.1.3 Обобщение способов поиска решения многих задач до системы советов

В процессе решения задачи деятельность учащегося направлена на понимание задачи, осуществление поиска ее решения. Таким образом, она направлена на осознание, систематизацию и выяснение той информации, которая является явной в задаче.

Советы при решении различных задач должны обладать общностью, должны быть естественны и просты.

Все советы можно разделить на четыре группы, которые соответствуют четырем этапам решения задачи: усвоение содержания задачи; составление плана решения задачи; реализация плана решения задачи; анализ и проверка правильности решения [30]. На первом этапе деятельности целью является достижения осознанного понимания словесной формулировки задачи. Взгляд на один и тот же факт или объект задачи с различных сторон помогает оценить связь объекта задачи с другими данными или внешней информацией. На втором этапе должны быть установлены связи различных объектов в задаче и выявлена связь с внешней информацией, с ранее приобретенным опытом. Учащийся должен внимательно, многократно и с разных сторон рассмотреть все компоненты задачи, их внутренние и внешние связи и осуществить составление плана решения задачи. На третьем этапе осуществляется сам план решения задачи, на четвертом – исследование полученного решения.

Такие этапы помогают направить ход мыслей в нужном направлении для достижения поставленной в задаче цели. Рассмотрим подробно систему советов, например, для составления плана решения задачи.

Это второй этап решения задачи, наступает, когда ученик вник в содержание задачи, ввел все обозначения, по необходимости сделал чертеж.

Для составления верного плана решения задачи необходима подготовка.

А). Для начала следует выяснить, известна ли какая-либо родственная задача? Аналогичная задача?

Пример 12. За одно и то же время велосипедист проехал 4 км, а мотоциклист – 10 км. Скорость мотоциклиста на 18 км/ч больше скорости велосипедиста. Найдите скорость велосипедиста.

Пример 13. Лодка за одно и то же время может проплыть 36 км по течению реки или 20 км против течения. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч [17].

Задачи аналогичны по плану решения. В обеих для решения необходимо составить отношения расстояний к скоростям и приравнять. Общая формула выглядит следующим образом: 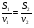. Если при решении задач, одна уже была рассмотрена ранее, то другая может быть решена по аналогии.

Б). Подумать, известна ли задача, к которой можно свести решаемую?

Пример 14. Отрезки, концами которых служат внутренние точки противоположных сторон квадрата, перпендикулярны. Докажите, что эти отрезки равны [38].

Решение задачи упрощается, если заданная пара взаимно перпендикулярных прямых будет проходить через центр квадрата. Доказав равенство отрезков в этом случае, основная задача легко решается использованием признаков параллельности и определения квадрата. Таким образом задачу можно свести к следующей: Отрезки, концами которых служат внутренние точки противоположных сторон квадрата, перпендикулярны и пересекаются в центре квадрата. Докажите, что эти отрезки равны.

В). Если родственная задача неизвестна и свести данную задачу к какой-либо известной задаче не удается, то стоит воспользоваться советом: «Попытайтесь сформулировать задачу иначе». При переформулировании задачи либо пользуются определениями данных в ней математических понятий (заменяют термины их определениями), либо их признаками (точнее сказать, достаточными условиями).

Пример 15. Найти периметр правильного шестиугольника A₁A₂A₃A₄A₅A₆, если A₁A₄ = 2,24 см [1, №1131].

Для быстрого и более легкого нахождения плана

решения данной задачи, удобно к понятию «правильный

Рис. 1

шестиугольник» добавить определяющий признак, что

«в правильном шестиугольнике».

Тогда задача примет вид: Найти периметр правильного шестиугольника

A₁A₂A₃A₄A₅A₆, в котором отрезки, соединяющие его центр с вершинами равны сторонам правильного шестиугольника, если A₁A₄ = 2,24 см.

Тогда, глядя на рисунок 1, становится ясен план решения задачи.

Г). Так же, составляя план решения задачи, следует задать себе вопрос: «все ли данные задачи использованы?» Выявление неучтенных данных задачи облегчает составление плана ее решения. Возможно, имеются «скрытые» данные.

Пример 16. Найти диагональ прямоугольного параллелепипеда, длина а, ширина b, высота h которого известны [30].

Так может случиться, что ученик, зная теорему Пифагора, найдет диагональ грани: 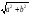. Далее самостоятельное решение задачи будет для него уже затруднительно, тогда учитель, задав вопрос «все ли данные задачи использованы?», может помочь ученику в отыскании верного пути решения задачи.

Д). Иногда полезно следовать совету «Попытайтесь преобразовать искомые или данные». При этом данные преобразуют так, чтобы они приблизились к искомым.

Пример 17. Постройте треугольник, равновеликий данному четырехугольнику [38].

При отыскании решения данной задачи следует для начала преобразовать четырехугольник до параллелограмма, так как формулы площадей треугольника и параллелограмма сходны между собой.

Е). Если следуя предыдущим советам, вам не удалось составить план решения, то можно воспользоваться таким советом: «попробуйте решить лишь часть задачи», т.е. попробуйте удовлетворить лишь части условий, с тем, чтобы далее искать способ удовлетворить оставшейся части условий задачи. Этот совет можно расширить, развить до совета: «Расчлените задачу на более простые задачи».

Рис. 2

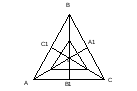
Пример 18. В треугольнике ABC медианы AA₁, BB₁, CC₁ пресекаются в точке M. Точки A₂, B₂, C₂являются соответственно серединами отрезков AM, BM, CM. Докажите, что A₁B₁C₁= A₂B₂C₂ [1, №1177].

Данная задача решается с применением центральной симметрии,

которая явно не видна (рис. 2). Тогда стоит разбить задачу на этапы:

1) установить взаиморасположение точек A₁, B₁, C₁и A₂, B₂, C₂;

2) найти центр симметрии; 3) определить центральную симметрию.

Ж) В составлении плана решения задачи может помочь ответ на вопрос: «Для какого частного случая возможно достаточно быстро решить эту задачу?». Отыскав частный случай, можно воспользоваться решением задачи в найденном частном случае для более общего (но, может быть, не самого общего) случая. Так можно поступить, постепенно обобщая задачу до исходной, решаемой задачи. Совет: «Рассмотрите частные случаи задачной ситуации, решите задачу для какого-нибудь частного случая, примените индуктивные рассуждения».

3). Иногда решение задачи оказывается проще, если сформулировать и решить задачу сначала более общую, а затем с ее помощью решить данную задачу. Совет: «Попробуйте сформулировать и решить более общую задачу».

Эвристико-организационные советы для решения задачи можно оформить в виде таблицы. [20] [Приложение 9]

Таким образом, с помощью индуктивных обобщений при решении математических задач можно вывести новые методы решения задач, перейти от одних методов решения задач к более общим. Так же индуктивные обобщения подходов к решению задачи их систематизация помогают в создании системы советов, полезных в процессе отыскания решения задачи.

2.2 Обобщение как метод решения математических задач

Обобщение как метод решения может осуществляться:

1. Решение задачи «по индукции»;

2. Решение задачи в «общем» виде.

2.2.1 Обобщения «по индукции»

Метод решения задачи «по индукции» основан на полной или теоретической индукции.

Обобщение как метод решения осуществляется по следующей схеме:

1. Выделить частный случай задачи, для которого задача решается легко и решить задачу для этого частного случая;

2. Рассмотреть более общий, но все же частный случай, содержащий первый;

3. Рассмотреть общий случай.

Часто решение задач «по индукции» включает в себя только первый и третий пункты из вышепредложеной схемы.

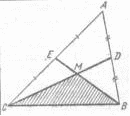
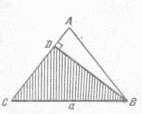
Пример 19. В четырехугольнике две стороны AD и BC не параллельны. Что больше: полусумма этих сторон или отрезок (MN), соединяющий середины двух других сторон четырехугольника (рис. 3а)? [3]

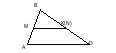
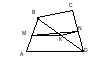
Рис. 3

1) Выделим для начала частный случай, который можно легко решить. В данном случае будет удобно, если одну из сторон четырехугольника стянуть в точку (рис. 3б). Тогда пусть BC стягивается в точку В. В таком положении точка N совпадает с серединой К отрезка BD, и MN становится средней линией MK треугольника ABD. Таким образом исходная задача сводится к следующей: что больше, половина стороны AD треугольника ABD или отрезок MK, соединяющий середины двух других сторон.

По определению средней линии треугольника ответ очевиден: MK=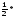AD

2) Теперь рассмотрим общий случай (Рис. 3в). Задача будет легко решена, если его свести к уже решенному частному случаю. Пусть K – середина диагонали BD четырехугольника ABCD. Из рассмотренного частного случая имеем: в треугольнике ABD MK=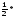AD и МК|| AD, в треугольнике BCD KN=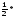BC и KN||BC.

Так как по условию AD не параллельно BC, то M, N, K не лежат на одной прямой. Тогда по правилу треугольника, в треугольнике MKN видно, что MN<MK+KN = (AD+BC).

Следовательно, мы доказали, что полусумма сторон AD и BC четырехугольника ABCD больше чем отрезок (MN), соединяющий середины двух других сторон.

Каждый раз при решении общей задачи используется результат решения предыдущей частной задачи. Такой частный случай Д. Пойа называет ведущим [30].

Рассмотрим использование различных частных случаев при решении задач.

Пример 20. Дана окружность радиуса R. Из точки A, лежащей вне окружности и отстоящей от центра O на расстоянии а, проведена секущая. Точки B, C ее пересечения с окружностью соеденены с центром О. Пусть 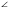BOA и COA обозначены соответственно через 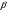и 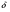. Найти 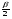tg*tg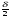(рис. 4а).

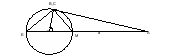
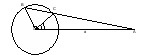
Рис. 4

Так как требуется найти величину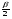 tg* tg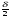 в зависимости от данных, то есть а и R, то ответ должен быть одним и тем же при любом выборе секущей. Тогда верно, что этот же ответ должен получиться и при случае, когда секущая вырождается в касательную (рис. 4б). В данной задаче в качестве частного случая следует рассмотреть случай, когда проведена не секущая, а касательная.

Обобщение «по индукции» удачно подходит для вывода площадей поверхностей многогранников.

Пример 21. Вывести формулу боковой поверхности правильной nугольной призмы.

Вначале можно вывести формулу площади боковой поверхности прямой правильной треугольной призмы.

Далее обобщаем задачу до вывода формулы площади боковой поверхности прямой правильной nугольной призмы.

Иногда при решении задачи необходимо рассмотреть несколько вариантов, исчерпывающих все частные случаи, о чем прямо в задаче не сказано. Тогда метод будет иметь несколько другую схему рассуждений:

1) выделить все варианты частных случаев ситуации, описанной в задаче или создавшейся при ее решении;

2) решить задачу для каждого варианта;

3) объединить решения всех вариантов.

Часто этот метод называют методом исчерпывающих проб. Применение метода возможно при конечном числе вариантов.

Пример 22. Найти все четырехзначные числа, удовлетворяющие условиям: сумма цифр равна 11, само число делится на 11.

Обозначим искомое число: abcd=10³*a+10²*b+10*c+d.

Запишем условия задачи в систему: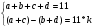

Второе уравнение системы выражает делимость искомого числа на 11. Преобразовав систему, получим уравнение: 2*(a+c)=11*(k+1), причем k 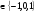, так как разность в левой части второго уравнения не может быть меньше -11 и больше 11 (сумма цифр равна 11).

Тогда возможны три случая:

k=-1, тогда a+c=0, тогда a=0, что противоречит условию (число четырехзначное).
k=0, тогда 2*(a+c)=11, чего не может быть.
k=1, тогда a+c=11, b=0, d=0 и все значения a и с можно записать в таблицу 2:

Табл. 2

Число вариантов конечно, снова решив задачу для каждого варианта, находим, что решением задачи будут числа 2090, 3080, 4050, 5060, 6050, 7040, 8030,9020.

Таким образом, чтобы применять обобщение как метод решения задачи «по индукции», нужно уметь выделять частные в случаи задаче.

2.2.2 Решение задач «в общем виде»

Необходимо обучать школьников решению задач «в общем» виде, так как решение задачи «в общем» виде часто может оказаться доступнее, легче, рациональнее, чем решение конкретной задачи. Так же обобщенная формулировка задачи помогает усвоению математической сущности конкретных задач и позволяет обнаружить способ решения исходной задачи. К более общей задаче могут быть применимы методы, которые не применимы к исходной задаче.

Обобщенная задача иногда подсказывает новый способ решения.

Пример 23. Вычислить |a| – 2*|a| + 9*|a|²+35*|a|⁵-21*|a|³-5*|a|⁴ при a равных -2; 1.

Так как модуль раскрывается в зависимости от того, какой знак имеет подмодульное выражение, то обобщением задачи может быть следующая задача: Найти значение выражения F(a), если a<0; a >=0.

Обобщенная задача помогает прояснить суть конкретных задач. При a<0 учащиеся поймут суть раскрытия модуля с отрицательным знаком, при a >=0 с положительным.

Иногда задачу удобнее решать сформулировав ее в общем виде.

Пример 24. Даны правильный октаэдр и прямая занимают в пространстве фиксированное положение. Найти плоскость, проходящую через данную прямую и делящую октаэдр на две равновеликие части [30].

Эта задача может показаться сложной, поэтому рациональнее ее сформулировать в общем виде, используя знания о правильном октаэдре: «Даны замкнутая поверхность, обладающая центром симметрии, и прямая занимают в пространстве фиксированное положение. Найти плоскость, проходящую через данную прямую и делящую объем тела, ограниченного данной поверхностью, на две равновеликие части». Искомая плоскость должна проходить через центр симметрии поверхности и определяться этой точкой и данной прямой. Так как октаэдр обладает центром симметрии, тем самым первоначальная задача оказывается найденной.

Так же следует использовать решение задачи в «общем виде» и в задачах с конкретными значениями, но решения которых громоздки. Решение задачи в «общем» виде с последующей подстановкой числовых данных часто позволяет лучше просмотреть план решения задачи, сократить записи, затратить меньше времени на вычисления.

Таким образом, при использовании обобщения как метода решения задач необходимо уметь выделять частные случаи. Так же полезно обучать школьников решению задач в общем виде, так как часто обобщенную задачу решить легче, чем конкретную задачу.

2.3 Обобщение как источник новых математических задач

Обобщения при обучении решению математических задач могут способствовать возникновению новых задач. Новые задачи могут появиться как при исследовании конкретной задачи и ее решения, так и при исследовании обобщенной задачи и ее решения.

К возникновению новой обобщенной задачи могут привести индуктивные обобщения. Обратная операция – специализация, позволяет от обобщенной задачи перейти к конкретным задачам.

Так же с помощью обобщений по аналогии из одной конкретной задачи получают новые конкретные задачи, из обобщенной задачи – новые обобщенные задачи.

Получение новых задач важно тем, что при составлении задач учащиеся усваивают структуру задачи, взаимосвязь данных, данных и искомых, обнаруживают внутреннюю связь между задачами.

Для того чтобы получить новые задачи при помощи обобщений, используют следующие приемы:

1) обобщение данных при сохранении искомых;

2) обобщение (добавление) искомых при сохранении данных;

3) обобщение данных и искомых.

Рассмотрим подробнее эти приемы.

2.3.1 Обобщение данных при сохранении искомых

Замена одних данных (или части данных) другими при сохранении искомых приводит к применению разнообразных приемов и методов решения, казалось бы, близких по содержанию задач. При этом может применяться не один прием, а широкий спектр методов.

Изменением условия задачи при сохранении требования может являться: замена данных более общими; замена одних отношений между объектами задачи другими.

Замена числовых данных задачи параметром часто приводит к обобщенной задаче. Специализация обобщенной задачи помогает получить целый класс аналогичных задач. Конкретные числовые данные можно заменять буквами не все сразу, а последовательно.

Пример 25. «Найти, если сторона нижнего основания равна 10 м, сторона верхнего 5 м и высота пирамиды 6 м» [30].

Если числа 10, 5, 6 заменить буквами, например а, b, h, получим обобщенную задач: «Найти объем усеченной пирамиды с квадратным основанием, если сторона нижнего основания равна a, сторона верхнего b и высота пирамиды h». Перейдя от задачи «в числах» к задаче «в буквах», мы воспринимаем данные величины как переменные.

Обобщенная задача дает возможность составить и решить еще несколько типов задач, в которых одна из величин является искомой, а остальные – данными.

К появлению новых задач так же приводит обобщение понятий, данных в задаче.

Пример 26. Найти диагональ куба, если даны три его измерения (длина, ширина и высота).

Обобщив понятие куба до понятия прямоугольного параллелепипеда, получим новую задачу:

Пример 27. Найти диагональ прямоугольного параллелепипеда, если даны три его измерения (длина, ширина и высота).

Замена одних отношений между объектами задачи другими тоже может привести к появлению новых задач.

Пример 28. Как изменится частное двух чисел если делимое увеличить в три раза?

Можно исследовать эту задачу и получить новые, размышляя, что произойдет с частным, если делимое увеличить в 3 раза, уменьшить в 3 раза, если изменить делитель, если изменить одновременно делимое и делитель? Возникает целая серия задач, порожденных данной задачей, которые можно записать в таблицу 3.

Табл. 3

Условие задачи

Вопрос задачи

• Если делимое увеличить в 3 раза

• Если делимое уменьшить в 3 раза

• Если делитель увеличить в 3 раза

• Если делитель уменьшить в 3 раза

• Если делимое и делитель увеличить в 3 раза

• Если делимое увеличить, а делитель уменьшить в 3 раза

• Если делимое уменьшить, а делитель увеличить в 3 раза

• Если делимое и делитель уменьшить в 3 раза

Как изменится разность?

После решения конкретных задач полезно сделать обобщения: если делимое и делитель увеличить или уменьшить в одно и то же положительное число раз, то не изменится; если делимое увеличить, а делитель уменьшить в одно и то же положительное число раз, то частное увеличиться в квадрат этого числа; если делимое уменьшить, а делитель увеличить в одно и то же положительное число раз, то частное уменьшится в квадрат этого числа.

Изменяя отношения между данными задачи, делая их более общими так же можно получить новые задачи.

Пример 29. Доказать, что сумма расстояний, от точки пересечения медиан правильного треугольника до его сторон постоянна.

От этой задачи можно перейти к следующей:

Пример 30. Доказать, что сумма расстояний, от точки взятой произвольно внутри правильного треугольника до его сторон постоянна.

2.3.2 Обобщение (добавление искомых) при сохранении данных

Новая математическая задача может быть получена с помощью изменения требования задачи при сохранении условия: добавления новых заключений; обобщения искомых.

В большинстве случаев в задаче встречается лишь один вопрос, одно заключение, но содержащаяся в задаче информация иногда позволяет сделать и другие выводы (ответить на другие вопросы, сделать другие заключения), т.е. добавить новые заключения при сохранении данных.

Пример 31. Даны две прямые a и b. Доказать, что любая прямая, пересекающая прямую a, пересекает и прямую b, то прямые a и b параллельны. [1]

Вначале требуется доказать параллельность прямых a и b. Тогда прямая, пересекающая a будет не только пересекать прямую b, но и обладать свойствами над этими прямыми: их накрест лежащие, соответственные и углы будут равны, а сумма односторонних будет равна 180⁰. Поэтому можно сформулировать более общую задачу.

Пример 32. Даны две прямые a и b. Доказать, что любая прямая, пересекающая прямую a, пересекает и прямую b, то прямые a и b параллельны, их накрест лежащие, соответственные и углы будут равны, а сумма односторонних будет равна 180⁰.

Задачи, которые приучают учащихся рассматривать всевозможные заключения из данных посылок, что бывает необходимо при решении многих задач на доказательство, при доказательстве различных теорем, иногда называют задачами «без вопросов». На основе решения таких задач удобно рассматривать обобщения о искомых в задаче.

Пример 33. Дана прямоугольная призма, в основании которой трапеция. Установите всевозможные взаиморасположения прямых, содержащих ребра данной призмы.

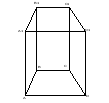Прямые, содержащие ребра данной призмы могут

находиться в трех положениях: быть параллельны,

пересекаться, быть скрещивающимися. Учащиеся, находя

Рис. 5

параллельные, скрещивающиеся и пересекающиеся прямые, делают выводы о свойствах призмы: что для каждой прямой, находящейся в плоскости одного основания всегда есть прямая, параллельная в плоскости другого основания; все прямые, содержащие боковые ребра параллельны; каждая прямая, содержащая боковое ребро, пересекается с двумя прямыми, содержащими ребра оснований, с остальными скрещивается.

2.3.3 Обобщение данных и искомых

Нередко обобщение данных задачи приводит к обобщению искомых.

Так, обобщение понятий, в условии задачи может привести к обобщению вопроса задачи. Таким образом, теорема косинусов является обобщением теоремы Пифагора.

Пример 34. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Пример 35. В произвольном треугольнике квадрат стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Обобщение данных и искомых задачи до параметра так же приводит к составлению новых задач. Например, зная, что правильный треугольник определяется любым элементом, можно составить задачи, связывающие между собой элементы правильного треугольника: стороны, медианы, радиусы вписанной и описанной окружностей.

Таким образом, мы показали как обобщения при обучении решению математических задач приводят в возникновению новых задач. Это происходит в результате исследования задач и их решений, а так же исследований обобщенных задач и их решений. Используя обобщение и специализацию, учащиеся могут сами составлять новые задачи, осуществляя замену части данных другими при сохранении искомых, добавляя новые заключения или обобщая искомые.

2.4 Обобщения задач ведущие к формированию понятий и теорем

С помощью обобщений можно осуществлять введение понятий и теорем. При этом происходит мотивация введения понятий и теорем, учащиеся сами осознают, как получили и для чего нужно новое знание, определяют его место в системе других понятий или теорем, и легко применяют его при решении различных задач.

При формировании понятий различают обобщения: 1) от конкретных примеров до математического понятия; 2) самих математических понятий.

К определению понятия часто приводит обобщение конкретных примеров.

Пример 36. Определение средней линии треугольника, в основном, в учебниках геометрии вводится дедуктивно. При этом большинство учащихся плохо усваивают определение средней линии треугольника или путают его с теоремой о средней линии треугольника.

Данное определение можно ввести, выделив отличительное свойство средней линии треугольника: соединение середин двух сторон треугольника.

Формирование понятия происходит в три этапа:

1) Выделение общего свойства у класса примеров. Глядя на рисунок 6, уместно задать вопрос ученикам: какими общими свойствами обладает линия

MN на рисунке?

Рис. 6

При таком обобщении учащиеся анализируют рисунки, находят в них общее свойство, которое сохраняется во всех данных рисунках: MN соединяет середины двух сторон треугольника. Это свойство включается в определение средней линии треугольника: средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

2) Осуществление специализации на следующем примере (рис. 7).

Необходимо найти средние линии.

Рис. 7

Так же вместе с примерами объектов, удовлетворяющих

определению понятия необходимо привести контрпримеры, объекты, которые к изучаемому понятию не относятся (рис. 8).

Рис. 8

Таким образом сформированное понятие четко осознается учащимися, а выделенное свойство и приведенные контрпримеры помогут быстро отличать его от других.

При обобщение планиметрии до стереометрии происходит большинство переходов от одних понятий к другим, более общим.

Пример 37. Обобщение параллельности прямых на плоскости до параллельности прямых в пространстве может осуществляться так: вспомнить определение параллельности прямых на плоскости: «Две прямые на плоскости называются параллельными, если они не пересекаются»; рассмотреть две прямые в пространстве. В результате беседы приходим к выводу, что для определения параллельности двух прямых в пространстве, необходимо, чтобы они принадлежали одной плоскости; обобщить определение параллельности прямых на плоскости до определения параллельности прямых в пространстве: «Две прямые в пространстве называются параллельными, если они принадлежат одной плоскости и не пересекаются».

По такому же принципу происходит обобщение квадрата до куба, площади параллелограмма до объема параллелепипеда, и другие.

Индуктивные обобщения при изучении теорем так же необходимы.

В основе любой теоремы лежит задача на доказательство. Поэтому осуществление обобщений при решении задач на доказательство позволяют учащимся увидеть возникновение теоремы, метода её доказательства, установить связь между различными теоремами, сформулировать новые, систематизировать теоремы и методы доказательства. Это облегчает проведение мотивации при введении теорем, приводит к осознанному восприятию идей доказательства, к пониманию и усвоению содержания теоремы, разумному применению теоремы для решения задач.

Индуктивные обобщения при решении задач на доказательство можно разделить на:

1) обобщение конкретных задач до формулировки теоремы;

2) обобщение теорем.

Индуктивное обобщение конкретных задач до теоремы состоит в том, что в результате сравнения и анализа решения нескольких конкретных задач можно выдвинуть гипотезу для общего случая и вывода теоремы.

Пример 38. Доказать, что если в четырехугольнике сумма противоположных углов равна 180⁰, то около этого четырехугольника можно описать окружность.

Задачу можно обобщить до формулировки теоремы:

«В любом вписанном четырехугольнике сумма противоположных углов равна 180⁰».

Возможно обобщение самих теорем до более общих. Любая доказанная теорема становится началом для открытия новых фактов и соотношений, доказательств новых теорем, т.е. входит в их доказательства.

Например, теорема о параллельности прямой и плоскости в пространстве обобщается до теоремы о параллельности трех прямых в пространстве, которая может быть обобщена до признака параллельности двух плоскостей.

При таких обобщениях расширяется множество объектов, к которым применимы рассматриваемые свойства и часто сохраняются методы доказательства.

Так же сами теоремы являются обобщениями ранее известных. Для соединения знаний в систему необходимо проводить обобщения теорем и показывать переходы от одних теорем к другим.

Так, обобщая теорему «площадь прямоугольного треугольника равна половине произведения катетов», отбросим ограничение, что треугольник прямоугольный и получим теорему «Площадь произвольного треугольника равна половине произведения двух сторон на синус угла между ними».

От теоремы «Середины сторон выпуклого четырехугольника являются вершинами параллелограмма» можно перейти к теореме «Точки, делящие стороны четырехугольника в одном и том же отношении (соединенные определенным образом) являются вершинами параллелограмма», а можно перейти к теореме стереометрии: «Середины сторон пространственного четырехугольника являются вершинами параллелограмма».

Таким образом, обобщение при формировании понятий и введении теорем очень полезно. Обобщение знания от конкретных задач до понятия и от задач на доказательство к доказательству теорем помогает проведению мотивации введения понятий и теорем, применению их при решении различных задач.

2.5 Таблицы как средство обобщения при обучении решению математических задач

При обучении решению математических задач удобно проводить обобщения, когда информация представлена в таблицах. Такие таблицы будем называть обобщающими.

Обобщающие таблицы служат для проведения сравнения и анализа математических задач и их решений, при систематизации способов и методов решения задач, при составлении системы советов для поиска решения задач, при выводе понятий и обобщении материала, используемого при решении задач.

При выводе метода решения задач удобно решение по этапам записывать в таблицу. При этом таблица будет состоять из двух столбцов: в первом – решение конкретной задачи, во втором – общий метод решения или алгоритм метода решения задач такого класса.

Для более глубокого понимания метода решения задачи очень эффективно дополнение таблицы еще одним столбцом, в котором показана специализация метода на еще одной конкретной задаче.

Пример 39. Общий алгоритм применения метода координат к решению математических задач можно вывести, проведя анализ решения задачи, к которой применим этот метод. Метод заключается во введении прямоугольной системы координат и записи условия задачи в координатах, после чего решение задачи легко провести с помощью алгебраических вычислений. Необходимо пошагово расписать решение задачи в первом столбце и записать обобщенный алгоритм решения во втором столбце [Приложение 10].

Так решение конкретной задачи приводит к выводу общего алгоритма решения класса задач методом координат:

Изучить условие задачи, ввести прямоугольную систему координат так, чтобы одна из точек фигуры являлась центром, и хотя бы одна сторона лежала на какой-либо оси.
Обозначить координаты точек во введенной системе координат
Используя нужную формулу, составить равенство, которое необходимо доказать, и доказать его в координатной форме.
Записать ответ.

Использование метода координат позволит решать и другие задачи.

После вывода алгоритма полезно сразу провести его специализацию на второй задаче, оформив все записи в таблицу.

Так же обобщающие таблицы удобно использовать при выводе нового понятия. При этом понятие формулируется на основе решенных задач, подводящих к его определению.

Пример 40. К определению понятия ромба можно подвести, решив три задачи определяющие его характеристические свойства и сделав вывод.

В учебнике [1] дается такое определение ромба: «Ромбом называется параллелограмм, у которого все стороны равны». Далее приводится особое свойство ромба: «Диагонали ромба взаимно перпендикулярны и делят его углы пополам». Для целостного осознания понятия «ромб» следует определение ввести вместе со свойством.

И так, требуется три задачи:

1) задача, подводящая к определению понятия: ромбом называется параллелограмм, у которого все стороны равны;

2) задача, подводящая к первой составляющей свойства ромба: диагонали взаимно перпендикулярны;

3) задача, подводящая ко второй составляющей свойства ромба: диагонали делят его углы пополам.

Все данные удобно оформить в таблицу [Приложение 11].

Решив все три задачи, следует приступить к заполнению четвертого столбца.

Из первой задачи следует определение ромба. Из условия второй задачи следует, что параллелограмм ABCD – ромб, и в нем диагонали пересекаются под прямым углом. Результатом решения третьей задачи является выяснение, что параллелограмм ABCD – ромб и к любому ромбу будет применимо условие задачи, что его диагонали делят углы пополам.

В результате такого способа формирования, понятие «ромб» гораздо лучше усваивается учащимися, чем введение понятия дедуктивно.

Широкое применение таблиц отмечается при обобщении материала, используемого при решении задач. Такие обобщающие таблицы могут быть использованы для различных целей: повторить и систематизировать знания, установить причинно-следственные связи между свойствами объектов, изложить материал укрупненными блоками, рационально заучить и воспроизвести материал [15].

Особое место среди обобщающих таблиц занимают динамические обобщающие таблицы. Они четко отражают взаимосвязи объектов в таблице и логику обобщения.

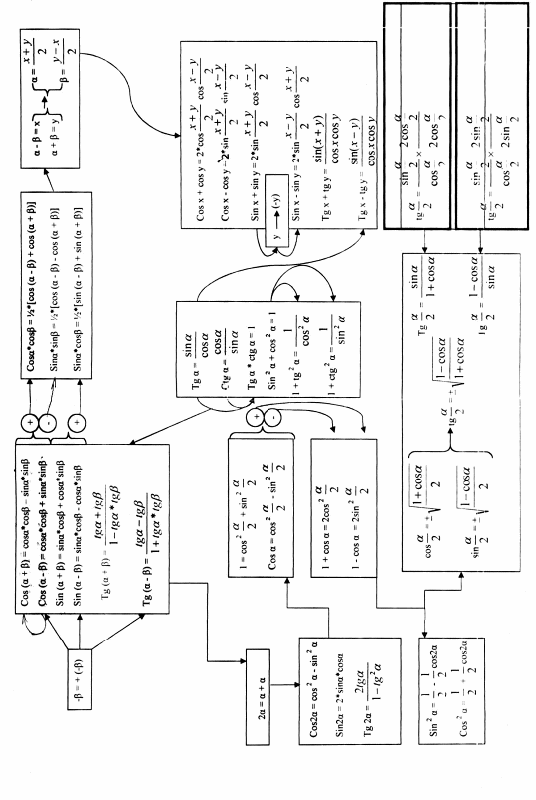
Примерами таких таблиц могут быть: обобщающая таблица свойств действительных чисел и векторов в школьном курсе математики [15] [Приложение 1] и сравнительная таблица связи векторов в геометрии и физике [15] [Приложение 2]. Примером обобщающей таблицы систематизации знаний учащихся может служить динамическая обобщающая таблица основных тригонометрических формул и их взаимосвязей [10] [Приложение 3].

Таким образом, для лучшего понимания процесса сравнения и анализа задач, при систематизации методов решения задач, при выводе понятий и обобщении материала, используемого при решении задач, удобно использовать обобщающие таблицы.

2.6 Опытное преподавание

Цель: апробация методических рекомендаций на уроках математики в 10-м классе, выявление их влияния на результативность обучения школьников решению задач.

Место проведения: муниципальное общеобразовательное учреждение гимназия №2 города Кирово – Чепецка Кировской области.

Время проведения: 2007–2008 учебный год.

Класс: 10

Учитель: Останина Ольга Александровна, учитель математики высшей квалификационной категории.

Содержание опытного преподавания.

Учитель систематически и целенаправленно в соответствии с методическими рекомендациями осуществлял обобщения решения задач при изучении различных тем алгебры и начала анализа и геометрии.

Приведем некоторые примеры использования обобщений.

Обобщение и систематизация теоретического материала по теме преобразование тригонометрических выражений учитель проводил при помощи динамической обобщающей таблицы основных тригонометрических формул и их взаимосвязей из пункта 2.5 [Приложение 3].

При изучении темы «производная» для формирования понятия производной осуществлялось индуктивное обобщение результатов решений задач из различных областей знаний (механики, геометрии, физики).

На основе сравнения и анализа решения конкретных задач был выявлен общий математический алгоритм решения для всех конкретных задач, которые приводят к новому математическому понятию – понятию производной. Все записи были оформлены в таблицу. [приложение 4]

После заполнения таблицы дается определение производной: производной функции f в точке х₀ называется предел отношения приращения функции к вызвавшему его приращению аргумента, вычисленный при условии, что приращение аргумента стремится к нулю, если этот предел существует и конечен.

Понятие производной позволило сформулировать другие понятия: мгновенной скорости тела («мгновенная скорость есть производная пути по времени»), углового коэффициента касательной к графику дифференцируемой функции («угловой коэффициент производная функции в этой точке f(х₀)»), мгновенной силы тока («мгновенная сила тока есть производная количества электричества по времени»).

При таком подходе учащиеся смогли осознать появление понятия и усвоить механический, геометрический, физический смысл производной, а так же научиться решать разнообразные задачи на приложения производной.

При изучении этой же темы проводилось обобщение решения конкретной задачи на отыскание наибольшего и наименьшего значения до метода решения класса задач на оптимизацию.

Для этого была выбрана конкретная задача, ее решение оформлялось в таблицу, состоящую из двух столбцов [приложение 5]. В левом столбце – решение конкретной задачи, в правом – решение обобщенной задачи.

Задача: сумма двух целых чисел равна 24. Найдите эти числа, если известно, что их произведение принимает наибольшее значение [25, №949а].

Таким образом был выведен общий метод решения задач на отыскание наибольшего и наименьшего значения.

Составленная схема решения задач на оптимизацию сравнивалась со схемой решения алгебраических текстовых задач и был сделан вывод, текстовые задачи алгебры и начал анализа решаются по одной схеме

Из решения данной конкретной задачи так же можно вывести следующее обобщение: «произведение двух чисел, если известна их сумма, будет наибольшим, если эти числа равны».

Обобщение как метод решения задач по индукции использовалось при выведении формулы площади боковой поверхности правильной nугольной призмы.

Вначале выводилась формула площади боковой поверхности правильной треугольной призмы.

Так как S_бок= P_осн*h, то для правильной треугольной призмы будет выполняться: S_бок= 3*а*h, где а – сторона правильного треугольника, находящегося в основании призмы.

Далее формула обобщалась до формулы площади боковой поверхности правильной nугольной призмы.

Так, S_бок= n*а*h, где а – сторона правильного nугольника, находящегося в основании призмы.

Все записи оформляем в таблицу [приложение 6].

Выведенная таким образом формула более понятна учащимся и сразу определяется класс задач, к которым она применима.

Обобщение как метод решения задач в «общем виде» был осуществлен при изучении темы «Многогранники» на уроке «Решение задач на призму», с целью показать, как иногда бывает более удобно решить задачу в общем виде, а потом подставить конкретные значения [Приложение 7].

Был сделан вывод, что решение задачи в общем виде и последующая подстановка числовых данных короче и производится быстрее по времени, так же яснее просматривается план решения задачи.

В результате апробации было установлено, что использование методических рекомендаций позволило повысить познавательную активность учащихся и результативность решения задач, что подтверждено рецензией учителя проводившего опытное преподавание.

Выводы по второй главе.

Таким образом обобщения при обучении решению задач являются эффективным средством поиска решения задачи и овладения общими методами решения задач.

Индуктивные обобщения при решении математических задач используются для вывода новых методов решения задач, перехода от одних методов решения задач к более общим, применимым к решению широкого класса задач. Так же индуктивные обобщения подходов к решению задачи их систематизация помогают в создании системы советов, полезных в процессе отыскания решения задачи.

Сами обобщения могут являться методом решения класса задач. При использовании обобщения как метода решения задач «по индукции» необходимо уметь выделять частные случаи. Полезно обучать школьников решению задач в общем виде, так как часто обобщенную задачу решить легче, чем конкретную задачу.

Обобщения приводят в возникновению новых задач. Необходимо проводить анализ задач и их решений, а так же обобщенных задач и их решений, при этом учащиеся могут сами составлять новые задачи, осуществляя замену части данных другими при сохранении искомых, добавляя новые заключения или обобщая искомые.

Введение понятий и теорем с помощью обобщения задач улучшает понимание вводимого знания, учащиеся сами осознают, как получили и для чего нужно новое знание, определяют его место в системе других понятий или теорем.

В результате проведения опытного преподавания было выявлено положительное влияние осуществления обобщений на результативность обучения школьников решению задач.

Заключение

В данной работе рассмотрены обобщения при обучении решению математических задач в курсе средней (полной) школы.

Цель работы достигнута, поставленные задачи выполнены.

В работе были рассмотрены обобщения при обучении методам решения математических задач, обобщение как метод решения математических задач, обобщение как источник новых математических задач, так же обобщения задач ведущие к формированию математических понятий и теорем.

Так же была показана роль таблиц как средства обобщения при обучении решению математических задач.

Опытное преподавание подтвердило выдвинутую гипотезу: если на уроках математики организовать процесс обучения решению задач в соответствии с предложенными методическими рекомендациями, то это позволит повысить результативность обучения школьников решению задач.

Библиографический список

Атанасян, Л.С. Геометрия 7–9 [Текст]: учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. – М.: Просвещение. 1996. – 336 с.
Атанасян, Л.С. Геометрия 10–11 [Текст]: учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. – М.: Просвещение. 1997. – 256 с.
Балк, Г.Д. О применении эвристических приемов в школьном преподавании математики [Текст] / Г.Д. Балк // Математика в школе. – 1969. – №5. – С. 21 – 28.
Бернштейн, М.С. Задачи на доказательство в курсе геометрии [Текст] / М.С. Бернштейн // Математика в школе. -1941. – №4. – С. 19–30.
Богушевский, К.С. Из писем и заметок читателей [Текст] / К.С. Богушевкий // Математика в школе. -1952. – №5. – С. 60–72.
Болтянский, В.Г. Анализ – поиск решения задач [Текст] / В.Г. Болтянский // Математика в школе. – 1974. – №1. – С. 34 – 40.
Выготский, Л.С. Избранные педагогические исследования[Текст] / Л.С. Выготский, Л.С. – М.:Изд-во АПНРСФСР, 1956. – 519 с.
Горский, Д.П. Краткий словарь по логике [Текст] / Д.П. Горский, А.А. Ивин, А.Л. Никифоров; Под ред. Д.П. Горского. – М.: Просвещение, 1991. – 208 с.
Горский, Обобщение и познание Д.П. Горский. – М.: Мысль. 1985. – 208 с.
Груденов, Я.И. Совершенствование методики работы учителя математики [Текст]: кн. для учителя / Я.И. Груденов. – М.: Просвещение, 1990. – 224 с.
Дорофеев, Г.В. Обобщение метода интервалов [Текст] / Г.В. Дорофеев // Математика в школе. – 1969. – №З.-С. 39–44.
Зильберберг, Н.И. Урок математики [Текст]: подготовка и проведение: кн. для учителя / Н.И. Зильберберг. – М.: Просвещение; Учеб. лит., 1995. – 178 с.
Изаак, Д.Ф. Обобщение задач по геометрии [Текст] / Д.Ф. Изаак // Математика в школе. – 1983. – №2. – С. 55 – 57.
Канин, Е.С. Заключительный этап решения учебных задач [Текст] / Е.С. Канин, Ф.Ф. Нагибин // Преподавание алгебры и геометрии в школе / сост. О.А. Боковнев. – М., 1982. – С. 131–139.
Канин, Е.С. Учебные математические задачи [Текст]: учеб. пособие / Е.С. Канин. – Киров: Изд – во Вят. ГГУ, 2003. – 191 с.
Кретинин, О.С. формирование приемов обобщения и специализации в 5 классе [Текст] / О.С. Кретинин // Математика в школе. – 1972. – №2. – С. 28 – 30.
Кузнецова, Алгебра. 9 кл [Текст]:сборн. зад. для проведения письм. экз. по алгебре за курс осн. школы / Л.В. Кузнецова, Е.А. Бунимович, Б.П. Пигарев, С.Б. Суворова. – М.: Дрофа, 1996. – 144 с.
Кушнир, И.А. Об одном способе решения задач на построение [Текст] / И.А. Кушнир // Математика в школе. – 1984. – №2. – С. 22 – 25.
Маланюк, М.П., Гапюк, Я.Ф. Упражнения обобщающего характера в курсе алгебры 6 класса [Текст] / М.П. Маланюк, Я.Ф. Гапюк // Математика в школе. – 1984. – №2. – С. 25 – 27.
Малых, Е.В. Обобщения в обучении математике учащихся полной средней школы [Текст]: дисс. … канд. пед. наук. Киров. 2005.
Методика обобщающих повторений при обучении математике [Текст]: пособие для учителей и студентов / В.А. Далингер. – Омск: изд-во ОГПИ. 1992. – 88 с.
Методика преподавания математики в средней школе. Общая методика [Текст]: учеб. пособие для студентов пед. ин-ов / А.Я. Блох, Е.С. Канин; сост. Р.С. Черкасов, А.А. Столяр. – М.: Просвещение. 1985. – 336 с.
Методика преподавания математики в средней школе. Общая методика [Текст]: учеб. пособие для студентов физ. – мат. фак. пед. ин-ов / В.А. Оганесян, Ю.М. Колягин, Г.Л. Луканкин, В.Я. Саннинский. – М.: Просвещение. 1980. – 368 с.
Мордкович, А.Г. Алгебра и начала анализа. 10–11 кл. [Текст]: учеб. для общеобразоват. учреждений / А.Г. Мордкович. – М.: Мнемозина, 2003. – 375 с.
Мордкович, А.Г. Алгебра и начала анализа. 10–11 кл. [Текст]: задачник для общеобразоват. учреждений / А.Г. Мордкович, Л.О. Денищева, Т.А. Корешкова, Т.Н. Мишустина, Е.Е. Тульчинская; под ред. А.Г. Мордковича. – М.: Мнемозина, 2004. – 315 с.
Мордкович, А.Г. Беседы с учителями математики [Текст]: Концептуал. методика. Рекомендации, советы, замечания. Обучение через задачи / А.Г. Мордкович. – М.: Школа-Пресс, 1995. – 272 с.
Островский, А.И. Геометрия помогает арифметике [Текст] / А И. Островский, Б. А Кордемский. – М: Физматгиз, 1960. -168 с.
Педагогика [Текст]: учеб. пособие для студентов пед. ин-ов / Ю.К. Бабанский, В.А. Сластенин, Н.А. Сорокин; под ред. Ю.К. Бабанского. 2 – е изд., доп. и перераб. – М.: Просвещение, 1988. – 479 с.
Педагогический энциклопедический словарь [Текст] / гл. ред. Б.М. Бим – Бад. – М: Большая Российская энциклопедия, 2002. – 528 с.
Пойа, Д. Как решать задачу [Текст]: пер. с англ. / Д. Пойа. – М.: Учпедгиз, 1959. – 216 с.
Пойа, Д. Математика и правдоподобные рассуждения [Текст] / Д. Пойа. – М.: Наука, 1975. – 464 с.
Пойа, Д. Математическое открытие [Текст] / Д. Пойа. – М.: Наука, 1970. – 452 с.
Понарин, Я.П. Геометрия [Текст]: учебное пособие / Я.П. Понарин. – Ростов-на-Дону: Феникс, 1997. – 512 с.
Психологический словарь / под ред. В.В. Давыдова, А.В. Запорожца, Б.Ф. Ломова; науч. – исслед. ин-т общей и педагогической психологии АПН СССР. – М.: Педагогика, 1983. – 448 с.
Родионов, М.А. Теория и методика формирования мотивации учебной деятельности школьников в процессе обучения математике [Текст]: дисс. … докт. пед. наук. – Саранск, 2001.
Розенфельд, Д.И. Об ознакомлении учащихся с методом обобщения [Текст] /Д.И. Розенфельд // Математика в школе. – 1965. – №1. – С. 41–43
Рубинштейн, С.Л. Основы общей психологии [Текст] / С.Л Рубинштейн. – СПб.: Питер Ком, 1998 – 688 с.
Саранцев, Г.И. Общая методика преподавания математики [Текст]: учеб. пособие для студентов мат. спец. пед. вузов и университетов / Г.И. Саранцев. – Саранск: Тип. «Крас. Окт.», 1999. – 208 с.
Семенов, Е.Е. Об одном приеме обучения учащихся обобщению и конкретизации [Текст] / Е.Е. Семенов // Математика в школе. – 1976. – №2. – С. 55 – 57.
Философская энциклопедия [Текст].Т4.-М.:Современная энциклопедия, 1967. – 519 с.
Философский энциклопедический словарь [Текст].Т4.-М.:Современная энциклопедия, 1983. – 446 с.
Фридман, Л.М., Турецкий Е.Н. Как научиться решать задачи [Текст]: кн. для учащихся ст. классов сред. шк./ Л.М. Фридман, Е.Н. Турецкий. – 3е изд., дораб. – М.: Просвещение, 1989. -192 с.
Эрдниев, П.М. Укрупнение дидактических едениц в обучении метематике [Текст]: кн. для учителя / П.М. Эрдниев, Б.П. Эрдниев. – М.: Просвещение, 1986. – 255 с.

Приложения

Приложение 1

Действительные числа

Векторы

1. Существуют отношения ра венства и неравенства

2. Есть ноль

2. Есть нулевой вектор

3. Существуют противоположные числа a + (– a) = 0

3. Существуют противоположные векторы: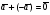

4. Определены действия сложения и вычитания чисел. Результат – число

4. Определены действия сложения и вычитания векторов. Результат – вектор.

5. Выполняются законы сложения

a + b = b +a,

a + (b + c) = (a + b) + c

5. Выполняются законы сложения:

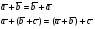
6. Определены действия умножения и деления чисел. Результат – число. Делить на 0 нельзя

6. Определено действие умножения (деления) вектора на число. Результат – вектор.

Определено скалярное умножение векторов. Результат – число.

7. Выплоняются законы умножения:

a*b=b*a

(a*b)*c=a*(b*c)

(a+b)*c=a*c + b*c

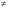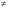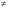a*b 0, если a0, b 0

7. Выплоняются законы умножения:

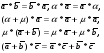
Не выполняется

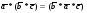
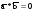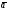
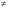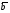
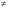может быть при 0, 0

8. Существует взаимно однозначное соответствие между множеством действительных чисел и точками координатной прямой

8. Существует взаимно однозначное соответствие между множеством векторов и точками координатной плоскости

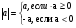
9. 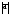– длина вектора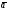

10. Направление на прямой

10. Направление на плоскости

Приложение 2

Векторы в геометрии

Векторы в физике

Вектор – направленый отрезок

Вектор – направленый отрезок: сила, скорость, ускорение, момент силы и т.п.

Скалярное умножение векторов

Работа:

при движении по наклонной плоскости
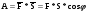
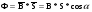где Ф – магнитный поток, В-магнитная индукция, S – площадь контура

Вычисление длины лектора

Нахождение значения равнодействующей силы, скорости и др.

Разложение вектора по координатным осям или по двум данным векторам

Разложение сил, скоростей, других векторных величин по координатным осям или двум данным векторам

Нулевой вектор

Сумма сил по замкнутому многоугольному контуру; сумма сил приложенных к центру тяжести фигуры

Компланарные вектора

Силы, скорости, ускорения и др., действующие в одном или противоположных направлениях

Некомпланарные векторы

Физические векторные величины, направленные друг к другу под углом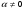

Приложение 3

Приложение 4

Задача о скорости движения (механика)

Задача о касательной к графику функции (геометрия)

Задача о мгновенной силе электрического тока (физика)

общий алгоритм решения этих задач

Найти мгновенную скорость движения тела в момент времени t.

Дан график функции f=f(x) и точка М(х₀, f(x₀)) на нем. В этой точке к графику проведена касательная (предположим что существует). Найти угловой коэффициент касательной.

Для цепи переменного тока определить силу тока в данный момент времени

Нахождение производной функции в заданной точке.

Обозначим зависимость пути от времени как функцию S=S(t).

Рассмотрим функцию f=f(x) дифференцируемую в заданной точке М

Рассмотрим зависимость количества электричества, протекающего через поперечное сечение проводника за время t как функцию Q=Q(t)

Выбираем некоторую функцию f=f(x).

зафиксируем какой то момент времени t, дадим аргументу t приращение t и рассмотрим ситуацию в момент времени

Зафиксируем х₀ и придадим приращение аргументу х. Получим точку х+х₀

Зафиксируем значение времени t₀, дадим аргументу t приращение t и рассмотрим промежуток времени от t₀ до t₀+t.

Зафиксируем х₀, придадим приращение аргументу х. Получим точку х+х₀

Найдем S(t), S (t+t) и вычислим приращение функции S (t+t) – S(t)= S.

Найдем f(x₀), f(x₀+x) и вычислим приращение функции f(x₀+x) – f(x₀)= f. Через точки М(х₀, f(x₀) и М’ (x₀+x, f(x₀+x)) проведем секущую к кривой MM’.

Найдем Q(t₀), Q(t₀ + t) и приращение количества электричества Q = Q(t₀+t) – Q(t₀)

Найдем f(x₀), f(x₀+x), приращение функции f(x₀+x) – f(x₀)= f.

Найдем среднюю скорость v_ср.=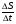

Тогда угловой коэффициент секущей будет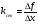

Найдем среднюю силу тока I_ср.=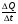

Составим отношение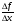

Тогда мгновенная скорость движения в момент времени t будет вычисляться как предел средней скорости при t->0: v_мгн.=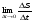

Учитывая, что касательная к кривой в точке М есть предельное положение секущей то при х->0 M’->M. Получаем:

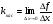
Мгновенная сила тока есть предел средней силы тока при t->0.

I_уд.=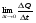

определяем условие существования предела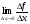

Это и есть мгновенная скорость движения тела.

Это и есть угловой коэффициент касательной

Это есть определение мгновенной силы тока.

Тогда предел 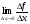есть производная функции f=f(x) в точке x₀ и обозначаетсяf’ (x₀)

Приложение 5

Решение конкретной задачи

Решение обобщенной задачи

сумма двух целых чисел равна 24. Найдите эти числа, если известно, что их произведение принимает наибольшее значение.

По исходным данным найти наибольшее или наименьшее значение какой-либо функции

1. Введем переменные: первое число равно х, второе – 24х

2. Ввести переменную, выразить через нее все остальные переменные задачи

2. Произведением двух чисел является функция P(x)=x (24х)

3. Составить функцию для исследования на экстремум

3. Так как х – целое число, а сумма двух чисел равна 24, то 0 < х < 24

4. Определить по условию задачи области задания функции

4. Задача свелась к нахождению такого значения х, при котором функция P(x)=x*(24х) принимает наибольшее значение на интервале (0; 24); P’ (x)= 24–2х; 24–2х = 0. Отсюда х = 12.

При х=12 функция P(x)=x*(24х) на интервале (0; 24) принимает наибольшее значение

5. Исследовать полученную функцию на экстремум, затем на наибольшее или наименьшее значение на области задания

5. Таким образом оба числа равны 12.

6. Записать ответ

Приложение 6

Вид призмы

Площадь боковой поверхности правильной треугольной призмы

Площадь боковой поверхности правильной nугольной призмы.

Чертеж

Общая формула площади боковой поверхности призмы

S_бок= P_осн*h

Вывод формулы площади боковой поверхности призмы необходимого вида

1) h – высота правильной треугольной призмы, в данном случае ребро призмы.

2) P_осн – периметр правильной треугольной призмы

В основании правильный треугольник -> P_осн = 3*a, где а – сторона правильного треугольника, находящегося в основании призмы

1) h – высота правильной nугольной призмы, в данном случае ребро призмы

2) P_осн – периметр правильной nугольной призмы

В основании правильный nугольник -> P_осн = n*a, где а – сторона правильного nугольника, находящегося в основании призмы

формула площади боковой поверхности призмы необходимого вида

S_бок= 3*а*h

S_бок= n*а*h

Приложение 7

Задача: Основанием наклонной призмы ABCA₁B₁C₁ является равнобедренный треугольник ABC, в котором AC=AB=13 см, BC=10 см, а боковое ребро призмы образует с плоскостью основания угол 45⁰. Проекцией вершины А₁ является точка пересечения медиан треугольника ABC. Найдите площадь грани CC₁B₁B» [2, №228].

Решение:

Вначале задача была решена по этапам. Этим была показана громоздкость решения и смотивировано отыскание решения задачи в «общем виде» с последующей подстановкой числовых данных.

1. Решение по этапам.

1) Так как треугольник ABC – равнобедренный, то AK является медианой и высотой. Тогда AK =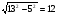

2) по свойству медианы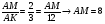

3) По условию задачи A₁AK=45⁰. Так как A₁M перпендикулярно плоскости основания, то треугольник A₁AM – равнобедренный, прямоугольный, следует A₁M=8

4) Тогда AA₁=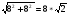

5) Так как ABCA₁B₁C₁ – призма, то AA₁=BB₁=CC₁

6) Тогда – параллелограмм. S_BB₁_CC₁=BB₁*BC,

то S_BB₁_CC₁=10*=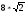

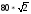
Ответ: S_BB₁_CC₁=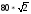

2. Решение задачи в общем виде с последующей

подстановкой данных короче и быстрее.

S_BB₁_CC₁=BB₁*BC; AA₁=BB₁=CC_1,то S_BB₁_CC₁=AA₁*BC =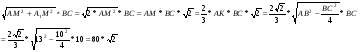

Приложение 8

Задача 1

Задача 2

Задача 3

Метод

Построить равнобедренный треугольник ABC (b=c) по а, h_b_.

Построить треугольник ABC по a, m_b, m_c

Построить ромб ABCD по диагонали BD и высоте ВН

Построение фигуры с помощью вспомогательного треугольника

1) Ищем вспомогательный треугольник: таким треугольником удобно считать CDB.

2) Это даст угол C, следовательно, и угол ABC.

3) есть а, B, C, значит, можно построить треугольник ABC

Схематично запишем:

– (a, h_b)->CDB-> C

– (a,B,C)-> ABC

1) Пусть M – точка пересечения медиан. Ищем вспомогательный треугольник: это CMB.

2) (2/3m_b,2/3m_c, a) дадут CMB, следовательно СBE и BCD

3) с помощью этих углов можно построить стороны b, с.

– (m_b, a, СBE)-> СBE->1/2b

– (m_c, a, BCD)-> DCB->1/2c

– (b, c, a)-> ABC

1) Ищем вспомогательный треугольник: так как известна высота и диагональ, то этоBHD.

2) это даст 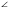BDH.

3) Теперь можно построить равнобедренный треугольник BDA, а следовательно, и ромб ABCD.

1) Проанализировать условие задачи и найти вспомогательный треугольник.

Произвести чертеж.

2) Определить элементы вспомогательного треугольника, с помощью которых возможно дальнейшее построение искомой фигуры.

3) произвести дальнейшее построение.

Приложение 9

Вопросы и советы для усвоения содержания задачи

А). Сначала следует ознакомиться с задачей, внимательно прочитав ее содержание. При этом схватывается общая ситуация, описанная в задаче.

Б). Ознакомившись с задачей, необходимо вникнуть в ее содержание. В задаче на нахождение выделить данные и искомые, а в задаче на доказательство – посылки и заключения.

В). В том случае, когда данные (или искомые) в задаче не обозначены, надо ввести подходящие обозначения.

Г). Часто пониманию задачи помогает разделение условия на части и запись каждой части условия с помощью введенных обозначений.

Д). Если задача геометрическая или связана с геометрическими фигурами, полезно к задаче и обозначить на чертеже данные и искомые.

Е). Полезно ответить на вопрос: «Возможно ли удовлетворить условию задачи?» Отвечая на него, полезно выяснить, однозначно ли сформулирована задача, не содержит ли она избыточных или противоречивых данных. Одновременно выясняется, достаточно ли данных для решения задачи.

Вопросы и советы для составления плана решения задачи

А). Известна ли вам какая-либо родственная задача? Аналогичная задача?

Б). Подумайте, известна ли вам задача, к которой можно свести решаемую?

Г). Составляя план решения задачи, следует задать себе вопрос: «все ли данные задачи использованы?» Выявление неучтенных данных задачи облегчает составление плана ее решения. Возможно, имеются «скрытые» данные.

Ж). Нередко в составлении плана решения задачи помогает ответ на вопрос: «Для какого частного случая возможно достаточно быстро решить эту задачу?» Обнаружив такой частный случай, можно воспользоваться решением задачи в найденном частном случае для более общего (но, может быть, не самого общего) случая. Так можно поступить, постепенно обобщая задачу до исходной, решаемой задачи. Совет: «Рассмотрите частные случаи задачной ситуации, решите задачу для какого-нибудь частного случая, примените индуктивные рассуждения».

Советы для реализации плана решения задачи

А). Проверяйте каждый свой шаг, убеждаясь, что он совершен правильно. Иными словами, нужно доказывать правильность каждого шага ссылками на соответствующие известные ранее математические факты, предложения.

Б). При реализации плана поможет совет: «Замените термины и символы их определениями».

В). При решении некоторых задач помогает совет: «Воспользуйтесь свойствами данных в условии объектов».

Анализ и проверка правильности решения задач

А). Проверьте результат.

Б). Проверьте ход решения.

В). Проверяя правильность хода решения, убеждаемся и в правильности результата. Совет: «Проверьте все узловые пункты решения».

Г). Второй способ проверки результата заключается в получении того же результата применением другого метода решения задачи, поэтому полезно ответить на вопрос: «Нельзя ли тот же результат получить иначе?» иными словами стоит следовать совету: «Решите задачу другим способом». Если при решении задачи другим способом получен тот же результат, задачу можно считать решенной правильно.

Приложение 10

шаги

Задача №1: докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.

Общий алгоритм

Задача №2: докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей.

Рассмотрим треугольник ABC, угол С-прямой. М – середина гипотенузы AB. Введем прямоугольную систему координат так, что С-центр, CBна оси х, СA – на оси у.

Вводим прямоугольную систему координат так, чтобы одна из точек фигуры являлась центром, и хотя бы одна сторона лежала на какой-либо оси.

АBCDданный параллелограмм. Введем прямоугольную систему координат так, что А-центр, AD – на оси х.

Обозначим: BC=a, AC=b, тогда вершины C (0,0), B (a, 0), A (0, b), М (a/2, b/2)

Обозначаем координаты точек во введенной системе координат.

Обозначим: AD=BC=a, тогда вершины A (0,0), B (b, c), D (a, 0), C (a+b, c)

Пользуясь формулой расстояния между двумя точками, найдем длины отрезков MC, MA:

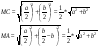
Используя нужную формулу, составляем равенство, которое необходимо доказать, и доказываем его в координатной форме.

Используя формулу расстояния между двумя точками, найдем:

AB²=b²+c²; AD²=a²; AC²=(a+b)²+c²; BD²=(a-b)²+c²

Отсюда:

AB²+BC²+CD²+DA²= 2*(AB²+AD²)=2*(a²+b²+c²), AC²+AD²=(a+b)²+c²+(a-b)²+c²= 2*(a²+b²+c²)

MA=MB=MC, что и требовалось доказать

Запись ответа

Таким образом, AB²+BC²+CD²+DA²=AC²+BD², что и требовалось доказать

Приложение 11

№

Задача

Решение задачи

Вывод

Определить вид четырехугольника ABCD его вид, если известно, что A+B=180⁰, A=смежному с D по продолжению AD и имеет место равенство: AB+CD=BC+AD

1) A+B=180⁰, то AD||BC (A и B – односторонние)

2) A= по продолжению AD, то AB||CD((A и смежному с D – соответственные).

Таким образом

ABCD – параллелограмм.

3) В параллелограмме

равенство: AB+CD=BC+AD

верно только при равенстве всех элементов, то есть AB=BC=CD=AD.

Делаем вывод: вид четырехугольника – параллелограмм, у которого все стороны равны.

Определение: параллелограмм, у которого все стороны равны называется ромбом

Дан, параллелограмм ABCD AB=BC=CD=AD. Доказать, что треугольник BOC – прямоугольный, где O – точка пересечения диагоналей.

1) AB=BC=CD=AD, треугольник ABC – равнобедренный.

2) В параллелограмме диагонали точкой

пересечения делятся пополам,

то есть OA=OC и BO – медиана.

3) В равнобедренном треугольнике

медиана является еще и высотой,

то есть BOC=90⁰

Таким образом треугольник BOC – прямоугольный

Так как в параллелограмме ABCD все стороны равны, то это ромб. Задача отражает свойство ромба: диагонали ромба взаимно перпендикулярны

В параллелограмме ABCDABD=DBC, AB=a. Найти периметр параллелограмма ABCD.

1) ABD=DBC. так как ABCD – параллелограмм, то DBC (накрест лежащие)

2) Тогда треугольник – равнобедренный

(ABD=BDA) и AB=AD=a.

3) Тогда в параллелограмме ABCD

все стороны равны и его периметр

равен 4*а

Выявили, что данный параллелограмм является ромбом. В ромбе справедливо, что его диагонали делят углы пополам

Листать вверх Листать вниз

Получить код

Скачать материал (0.72 Мб)

Нравится материал? Поддержи автора!

Ещё документы из категории педагогика:

Возможности развития элементарных способностей в условиях работы в классах коррекционно-развивающего обучения

Контроль как ведущий вид деятельности

Педагогічні умови соціалізації студентів засобами культури мовлення

Формування графічних умінь молодших школярів на уроках трудового навчання

Формы организации физического воспитания школьников

Формирование у учащихся практических познавательных умений по физике

Формирование внимания