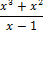
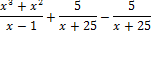
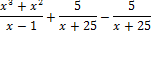
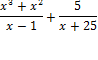
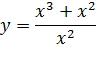
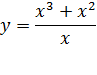
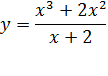
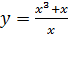
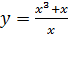
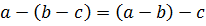
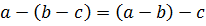
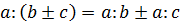
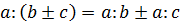
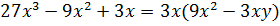
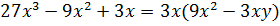
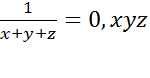
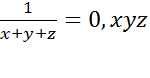
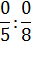
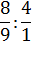
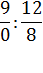
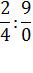
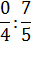
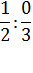
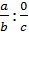
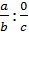
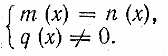
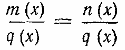
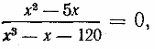
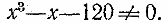
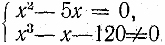
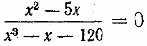
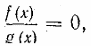
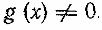
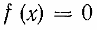
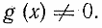
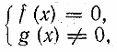
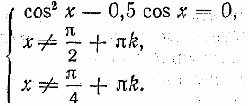
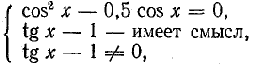
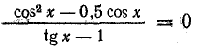
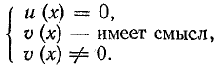
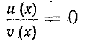
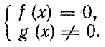
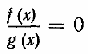
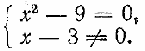
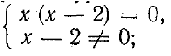
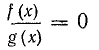
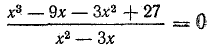
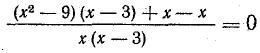
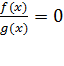
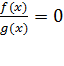
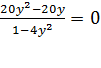
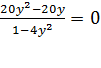
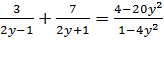
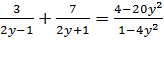
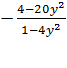
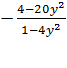
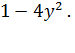
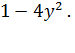
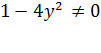
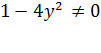
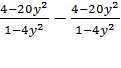
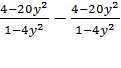
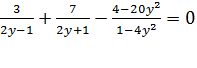
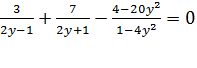
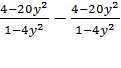
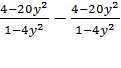
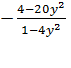
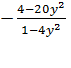
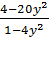
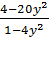
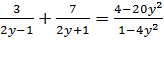
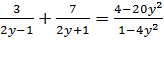
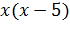
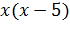
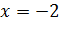
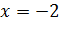
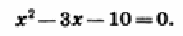
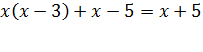
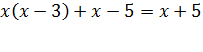
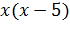
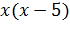
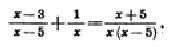
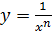
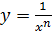
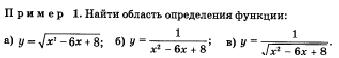
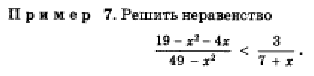
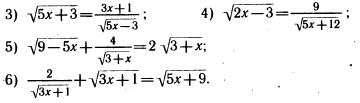
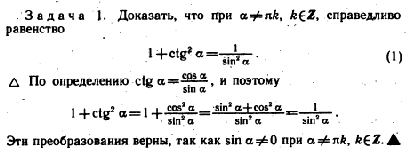
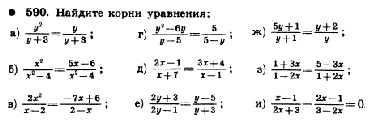
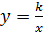
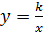
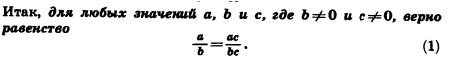
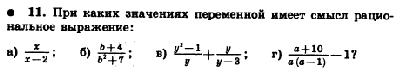
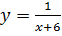
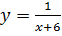
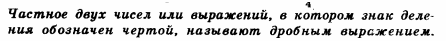
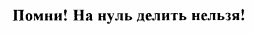
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

Физико-математический факультет

Кафедра дидактики физики и математики

КУРСОВАЯ РАБОТА

Профилактика затруднений школьников при обучении математике на примере темы «Уравнения с переменной в знаменателе»

Студента 4 курса

Маркова Романа Владимировича

Научный руководитель:

к.п.н., доцент кафедры дидактики

физики и математики

Шилова Зоя Вениаминовна

Киров 2009

Оглавление

Введение

Глава 1. Обзор учебников и методов изучения темы

1. Обзор учебников

2. Обзор методов изучения темы

Глава 2. Методические рекомендации по изучению темы

Заключение

Список литературы

Введение

С проблемой деления на ноль учащиеся знакомятся ещё в начальной школе, изучая операцию деления. Это связано с тем, что при делении на некоторое число используется умножение на число, обратное делителю, а число ноль, как известно из теории чисел, обратного элемента на множестве рациональных чисел не имеет. Но введение строгой аксиоматической теории в школьном курсе математики невозможно, поэтому проблема требует других, более понятных для школьника подходов.

Главным принципом при решении уравнений с переменной в знаменателе является учет именно этого факта, поэтому данная тема нуждается в пропедевтике. Анализ учебников математики (см далее.) показал, что во всех учебниках проблеме деления на 0 не отдается должного внимания. Как следствие – тема «уравнения с переменной в знаменателе» становится сложной и не доступной пониманию учащимся. Для уменьшения формализма при решении таких уравнений и затруднений при их решении в данной работе приводятся методические рекомендации для проведения пропедевтики темы, её изучения и последующего закрепления.

Объектом работы является преподавание математики и алгебры в 5 – 9 классах основной школы.

Предметом - затруднения школьников при обучении математике, а именно: проблемы, связанные с изучением темы «Уравнения с переменной в знаменателе».

Цель: разработать методические рекомендации, направленные на повышение качества знаний учащихся по теме «Уравнения с переменной в знаменателе», проведение пропедевтической работы с учащимися по теме, повторение изученного материала темы в ходе изучения других разделов алгебры.

Структура работы:

1. Обзор и анализ материала, предлагаемого к изучению по этой теме в основных школьных учебниках, методы изучения темы.

2. Методические рекомендации по изучению, пропедевтике и повторению материала темы.

Глава 1. Обзор учебников и методов изучения темы

1. Обзор учебников

Для анализа были выбраны следующие учебники:

3. Дорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и др. «Математика 5»

4. Истомина Н.Б. «Математика 5 класс»

5. Волович М. Б. «Математика 5»

6. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. «Математика 6»

7. Дорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и др. «Математика 6»

8. Истомина Н.Б. «Математика 6 класс»

9. Нурк Э.Р., Тельгмаа А.Э. «Математика 6»

10. Теляковский С.А. «Алгебра 7»

11. Алимов Ш.А., Ю.М. Колягин, Ю.В. Сидоров и др. «Алгебра: Учеб. Для 7 кл.»

12. Макарычев Ю.Н. «Алгебра 7 класс»

13. Теляковский С.А. «Алгебра 8»

14. Мордкович А.Г. и др. «Алгебра 8 класс»

15. Алимов Ш.А., Ю.М. Колягин, Ю.В. Сидоров и др. «Алгебра: Учеб. Для 9 кл.»

16. Мордкович А.Г. и др. «Алгебра 9 класс»

В каждом из учебников выбраны темы, каким-либо образом затрагивающие изучаемый раздел.

Дорофеев Г.В. и др. «Математика 5»

1. Введение операции деления:

2. Изучение операций с дробями. Случай деления на 0 не рассматривается.

Истомина Н.Б. «Математика 5 класс»

1. Операция деления. Случай деления на 0 не рассматривается, дана только краткая памятка:

2. Изучение операций с дробями. Случай деления на 0 не рассматривается.

Волович М. Б. «Математика 5»

1. Изучение операций с дробями. Случай деления на 0 не упоминается.

Виленкин Н.Я и др. «Математика 6»

1. Деление дробей. Случай деления на 0 не рассматривается.

2. Дробные выражения:

Деление на 0 не упоминается.

Дорофеев Г.В. и др. «Математика 6»

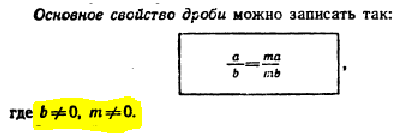
1. Основные сведения о дробях – основное свойство дроби:

2. Деление целых чисел. «На нуль, как обычно делить нельзя».

Истомина Н.Б. «Математика 6 класс»

1. Дроби и дробные выражения.

Деление на 0 не упоминается.

Нурк Э.Р., Тельгмаа А.Э. «Математика 6»

1. Деление обыкновенных дробей: «На нуль делить нельзя».

2. Деление рациональных чисел: «Обоснуй, что делить на 0 нельзя».

Теляковский С.А. «Алгебра 7»

1. Уравнения с 1 переменной и его корни: «Если обе части уравнения умножить или разделить на одно и то же отличное от 0 число, то получится уравнение, равносильное данному».

2. Нахождение корней линейного уравнения с 1 переменной: используется деление на не нулевой коэффициент.

3. Функция, график функции: нахождение области определения функции.

Пример:

Алимов Ш.А. «Алгебра 7»

1. Алгебраические равенства, формулы. Использование буквенных выражений:

2. Решение уравнений с одним неизвестным, сводящихся к линейным.

3. Алгебраическая дробь. Основное свойство дроби.

4. Функция, график функции. Тема не упоминается, понятие области определения не вводится.

5. Определение функции обратной пропорциональности для положительных Х. Неявное указание области определения.

Макарычев Ю. Н. «Аалгебра 7»

1. Выражения с переменными.

Далее приводятся задания для определения области допустимых значений переменной и нахождения значений переменных, при которых выражение не имеет смысла.

2. Уравнение с одной переменной: задания вида «укажите область определения уравнения»:

3. Функции и их графики. Область определения функции:

Пример задания:

Теляковский С. А. «Алгебра 8»

1. Рациональные дроби и их свойства.

Пример задания:

2. Сокращение дробей, основное свойство дроби:

3. Деление дробей.

4. Функция .

5. Решение дробных рациональных уравнений

Пример задания:

Мордкович А. Г. «Алгебра 8»

1. Алгебраические дроби. Основное свойство алгебраических дробей.

Случай деления на 0 не рассматривается.

2. Решение рациональных уравнений.

3. Гипербола, график гиперболы.

Случай 0 в знаменателе не рассматривается.

Алимов Ш. А. «Алгебра 9»

1. Функция, область определения функции.

2. Элементы тригонометрии. Пример применения темы:

3. Повторение – решение уравнений. Примеры:

Мордкович А. Г. «Алгебра 9»

1. Рациональные неравенства

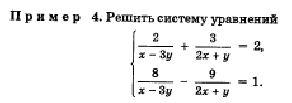
2. Системы уравнений

3. Функция, область определения

4. Функция и её график.

5. Тригонометрические функции.

Анализ приведенного материала

Проанализировав основные учебники, можно сделать вывод, что во всех учебниках 8 класса тема «рациональные уравнения» излагается довольно полно, однако, пропедевтика этой темы не приводится на достаточном уровне ни в одном учебнике. Отсюда у учащихся непонимание логики решения уравнений данного вида, формальный подход к их решению. Кроме того, в связи с частым использованием подобных уравнений в последующих темах, также необходимо повторение темы в 9 классе, которое в учебниках также мало представлено.

Темы, в которых затрагивается изучаемый раздел:

• Введение операции деления

• Изучение операций с дробями, основное свойство дроби.

• Деление целых чисел

• Деление рациональных чисел

• Уравнения с 1 переменной и его корни

• Функция, график функции: нахождение области определения функции

• Выражения с переменными

• Рациональные дроби и их свойства, деление дробей

• Функция «обратная пропорциональность»

• Решение дробных рациональных уравнений

• Элементы тригонометрии

• Рациональные неравенства

• Системы уравнений

1.Обзор методов изучения темы

Метод - умножения дробей на их общий знаменатель.

Для примера решим дробное рациональное уравнение

(1)

Умножим обе части уравнения на общий знаменатель дробей, т е на выражение . Получим целое уравнение

.(2)

Понятно, что каждый корень уравнения (1) является корнем уравнения (2). Но уравнение (2) может быть не равносильно исходному, так как мы умножили обе его части не на число, отличное от нуля, а на выражение, содержащее переменную, которое может обращаться в 0. Поэтому каждый корень уравнения (2) обязательно окажется корнем уравнения (1).

Упростив уравнение (2), получим квадратное уравнение

Его корни – числа -2 и 5.

Проверим, являются ли они корнями уравнения (1). При общий знаменатель не обращается в 0. Значит, число -2 – корень уравнения(1).

Итак, корнем уравнения (1) служит только число -2.

Вообще, при решении дробных уравнений целесообразно поступать следующим образом:

17. Найти общий знаменатель дробей, входящих в уравнение;

18. Умножить обе части уравнения на общий знаменатель;

19. Решить получившееся целое уравнение;

20. Исключить из его корней те, которые обращают в 0 общий знаменатель.

Метод, использующий равенство дроби 0.

Начнем с примера. Пусть требуется решить уравнение

(1)

Перенесем выражение в левую часть уравнения с противоположным знаком, т. е. прибавим к обеим частям уравнения по и разность в правой части уравнения заменим нулем. Получим уравнение

(2)

Может ли при переходе от уравнения (1) к уравнению (2) произойти потеря или приобретение корней?

Очевидно, что так как разность тождественно равна 0 на множестве тех значений у, при которых то мы могли бы приобрести новые корни за счет значений у, обращающих в нуль выражение Но они не могут служить корнями уравнения (2), так как при этих значениях выражение , входящее в качестве слагаемого в левую часть уравнения (2), теряет смысл.

Рассуждая аналогично, мы можем показать, что вообще уравнение r(х) = р(х), где r(х) и р(х) — рациональные выражения, причем хотя бы одно из них дробное, равносильно уравнению r(х) —p(x)=0

Вернемся к рассматриваемому примеру. Представив теперь cумму дробей в виде отношения двух многочленов, получим уравнение

(3)

Так как в результате преобразования суммы дробей в дробь мы получили выражение с той же областью определения и тождественно равное исходному выражению на этой области, то уравнение (3) равносильно уравнению (2), а следовательно, и уравнению (1).

Всякое ли преобразование дробного выражения r(х) — p(х) в дробь, числитель и знаменатель которой многочлены, позволяем от уравнения r(х) — р(х) = 0 перейти к равносильному уравнению вида , где f (х) и g (х) — многочлены?

Рассмотрим примеры.

Пример 1. Заменив в уравнении

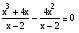(4)

выражение 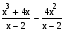дробью 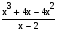и сократив эту дробь, мы получим уравнение х (х - 2) = 0, (5) не равносильное уравнению (4). Действительно, число 2 удовлетворяет уравнению (5), но не удовлетворяет уравнению (4).

Нарушение равносильности произошло за счет того, что мы выполнили тождественное преобразование, приводящее к выражению с более широкой областью определения: выражение 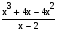определено при х2, а выражение х (х — 2) — при любом значении х.

Пример 2. В уравнении

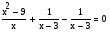(6)

заменим разность 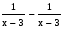числом 0. Получим уравнение

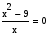(7)

Уравнение (7) не равносильно уравнению (6), так как существует такое значение переменной х (число 3), которое удовлетворяет уравнению (7), но не удовлетворяет уравнению (6).

Равносильность нарушена в связи с тем, что область определения выражения 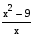шире, чем область определения выражения

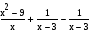
Если же при замене разности r (х) — р (х) рациональных выражений, хотя бы одно из которых дробное, дробью 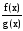, где f (х) и g (х) — многочлены, были выполнены только те тождественные преобразования, которые не меняют области определения выражения, то получится уравнение 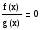равносильное уравнению r(х) — p(х) = О, а значит, и уравнению r(х) = р(х).

Так для уравнения (4) равносильным является уравнение

.

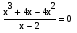Для уравнения (6) равносильным является уравнение

т. е. уравнение

Заметим, что в том случае, когда в ходе выполнения тождественных преобразований область определения выражения расширилась, предложением, равносильным уравнению r(х) — р(х) = 0, будет являться система, составленная из уравнения и ограничений, накладываемых на х в связи с изменением области определения. Например, для уравнения (4) равносильным предложением является система

для уравнения (6) — система

Для решения уравнения вида где f(х) и g(х) — некоторые многочлены, используется условие равенства дроби нулю: дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен от нуля. Поэтому уравнение указанного вида равносильно системе

Необходимо подчеркнуть, что здесь для нас существенным является тот факт, что выражение g(х) имеет смысл при любом х. В общем случае уравнение вида равносильно системе

Например, уравнение

равносильно системе

т. е. cистеме

Следует заметить, что при решении системы где

f(х) и g(х) — некоторые многочлены, вовсе не обязательно находить множество значений х, при которых Достаточно, найдя

корни уравнения , проверить, удовлетворяют ли они условию

В учебниках метод решения уравнений вида , где

f(х) и g(х) — целые выражения, разъясняется на примере уравнения

,

равносильного системе

.Учащиеся

не могут найти множество значений х при которых х ³— х — 1200, но этого и не требуется для решения системы. Непосредственная подстановка убеждает их, что из двух корней уравнения х² — 5х = 0, равных 0 и 5, только первый удовлетворяет условию Значит, рассматриваемая система, а следовательно и уравнение

,

имеет единственное решение — число 0.

При решении уравнения вида r(х) = р(х), где r(х) и р(х) — рациональные выражения, можно не сводить его к уравнению r(х) — р(х) = 0, а представить выражения r(х) и р(х) в виде дробей с одинаковыми знаменателями. Если при этом не выполнялись тождественные преобразования, которые могут привести к нарушению равносильности, то получится уравнение вида

,

где т(х), п(х), q(х) — целые выражения, равносильные уравнению r(х) = р(х). Уравнение указанного вида равносильно системе

Равносильность этих предложений можно доказать, опираясь на свойство числовых дробей: дроби с одинаковыми знаменателями равны тогда и только тогда, когда их числители равны, а общий знаменатель отличен от 0 (выражение q(х) имеет смысл при любом значении х).

С указанными способами решения уравнений вида r(х) = р(х), где r(х) или р(х) — рациональные выражения, хотя бы одно из которых дробное (так называемых уравнений с переменной в знаменателе дроби), учащиеся знакомятся в курсе алгебры VII класса.

Глава 2. Методические рекомендации по изучению темы

В этой главе даны краткие методические рекомендации по изучению каждой из выбранных тем с целью обеспечения наилучшего усвоения рассматриваемого понятия.

Введение операции деления

Углублять вопрос о нуле, как о числе в 5 классе преждевременно, но уже здесь надо со всей определенностью разъяснить невозможность деления на 0, подходя к этому вопросу двояко. Во-первых, разделить некоторое натуральное число на 0 значит узнать, сколько раз 0 содержится в , сколько раз надо взять слагаемым 0, чтобы получить ; ясно, что сколько бы нулей мы ни брали, сложение их не даст ничего, кроме 0; нельзя собрать рублей, если с каждого брать по 0 рублей. Во-вторых, разделить на 0 значит, найти такое число, которое при умножении на 0 даст , но любое число при умножении на 0 дает 0, а потому частного от деления на 0 не существует.

Пример обоснования этого факта из учебника Дорофеева: «Если бы захотели, например, найти частное 7:0, то это означало бы, что нужно найти такое число, которое при умножении на 0 даст 7. Но при умножении на 0 всегда получается 0. Поэтому частное 7:0 не существует. Говорят: «выражение 7:0 не имеет смысла».

В качестве дополнительных упражнений для закрепления этого факта можно использовать задание с формулировкой «Найти частное, или обосновать, почему его найти невозможно».

Пример:

6:2

0:8

4:4

15:3

16:0

9:3

Как дополнительный материал, можно рассмотреть результат деления 0:0, который, по логике приведенного доказательства, может быть любым числом.

Изучение операций с дробями, основное свойство дроби.

В этой теме также следует уделить внимание проблеме деления на 0, а именно, деления вида: , которое не упоминается ни в одном учебнике.

Проблема решается введением в систему упражнений подобных заданий с требованием обоснования полученного результата:

Это задание требует знания определения дроби, в котором заложено отличие знаменателя от 0, правила деления дробей, а также факта невозможности деления на 0, доказанного в предыдущем пункте.

В качестве дополнительных заданий, а также для повторения темы «Дроби» можно использовать выражения вида:

с формулировкой «Найти такие цифры x,y,z, что…».

Деление целых чисел

Тема изучается в 6 классе, по этому, требует повторения определения операции деления. Рекомендации те же, что для предыдущей темы – рассмотреть всевозможные случаи, в которых встречается 0, их, конечно, меньше, чем при делении дробей. Примеры: 0:2, 4:0, 0:0, обосновать результат, показать, почему на 0 делить нельзя.

Деление рациональных чисел

Тема схожа с делением дробей, с той разницей, что изучается она в 6 классе. Рекомендации те же, что в теме «Деление дробей».

Уравнения с 1 переменной и его корни

Не смотря на то, что случай переменной в знаменателе здесь еще не используется, следует обратить внимание учащихся на действия с уравнениями, а именно: «Если обе части уравнения умножить или разделить на одно и то же отличное от 0 число, то получится уравнение, равносильное данному».

Для закрепления можно использовать упражнения вида: «Равносильны ли уравнения»

5x=7 и (15-10)x=7+5x

17x-2=10x+4 и 0+7x=6

Также следует уделить внимание предупреждению основных ошибок, встречающихся при работе с уравнениями, а именно:

1. При разложении на множители способом вынесения общего множителя за скобки один из полученных сомножителей всегда будет многочленом, состоящим из того же числа членов, что и данный. Пример ошибки: . Решение проблемы – подробное следование алгоритму разложения на множители.

2. С распределительным законом умножения относительно сложения связана ошибка такого рода: . Причина – перенос распределительного закона, связывающего умножение со сложением на связь деления со сложением.

3. Еще одна ошибка связана с применением ассоциативного закона к неассоциативным операциям: .

Возможность появления этих ошибок следует учитывать при работе со всеми видами уравнений, неравенств, а также с многочленами.

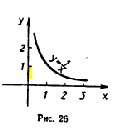
Функция, график функции: нахождение области определения функции

В этой теме необходимо пояснить нахождение области определения и вид графика функции при наличии переменной в знаменателе. Несмотря на то, что обратная пропорциональность и парабола еще не изучаются, их график школьники построить уже могут – с помощью таблицы.

Пример для рассмотрения: найти область определения функции и построить её график.

Область определения школьники найдут без труда, если перед этим актуализировать знания о делении и дробях, а с построением графика функции у них возникнут сложности. Решение проблемы:

изначально сказать, что функция определена только на своей области определения, а значит, в 0 не существует.

При построении графика функции (табличном) шаг таблицы в окрестности точки 0 брать меньше.

С учетом этих замечаний можно выполнить задания вида:

Выражения с переменными

Заданий на нахождение области определения в этой теме достаточно, однако стоит обратить внимание на обоснование запрета деления на 0, а также на задания вида: Сравните множества значений выражений

Функция «обратная пропорциональность»

К моменту изучения этой функции учащиеся должны знать про особенность её области определения (при необходимости можно повторить, решая задания на определение множества значений функции с переменной в знаменателе), что позволяет правильно начертить график (ОУ - асимптота). Изучение её поведения в окрестности точки 0, построение графика позволяют получить наглядное представление о проблеме деления на 0.

Решение дробных рациональных уравнений

Эта тема является основной в изучении данного вопроса, при соблюдении вышеуказанных рекомендаций, её изучение не должно вызвать трудностей, однако, перед началом изучения необходимо повторить следующие факты:

Обе части уравнения можно умножить или разделить на одно и то же не равное 0 число.

К обеим частям уравнения можно прибавить одно и то же число.

Условие равенства дроби 0: дробь равна 0, когда её числитель равен 0, а знаменатель не равен 0.

Далее следует рассмотреть алгоритм решения рационального уравнения с проверкой изменения множества допустимых значений на каждом шаге.

Есть 2 способа решения таких уравнений: традиционный и способ, использующий равенство дроби 0. (см. Глава 1)

Традиционный способ прост и алгоритмичен, но решение уравнений такого вида традиционным способом «отбрасывания знаменателя», который заключается в том, что левая и правая части уравнения представляются в виде дробей, а затем умножаются на общий знаменатель дробей неудачно. Учащиеся плохо понимают, на чем основано «отбрасывание знаменателя», а приобретенное умение переносят на тождественные преобразования дробных выражений, что влечет за собой грубейшие ошибки.

Использование условия равенства дроби нулю или условия равенства двух дробей позволяет добиться более глубокого понимания существа дела и значительно снизить число ошибок, допускаемых учащимися при решении уравнений указанного вида.

Однако, несмотря на простоту обоснования, второй способ более сложен, потому что при нем необходимо проверять изменения области определения уравнения при каждом преобразовании.

Итак, для решения таких уравнений используется 2 альтернативных метода, один – более алгоритмичен, но его обоснование не доступно ученикам, второй прост в обосновании, относительно сложен в реализации, но очень полезен при решении более сложных уравнений, когда учитываются не только нули знаменателя, но и область определения более сложных (тригонометрических, логарифмических, степенных, показательных) функций.

В качестве дополнительных упражнений, особенно для второго метода, необходимо включить в систему задач следующие:

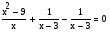
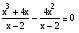
Подобные уравнения показывают, что необдуманное приведение подобных слагаемых или сокращение дроби приводит к расширению области определения.

Элементы тригонометрии, Рациональные неравенства, Системы уравнений

В этих темах широко используются методы решения рациональных уравнений, по этому, закрепление данной темы в основной школе происходит именно в этих разделах.

Заключение

Уравнения с переменной в знаменателе – сложная для усвоения тема, она требует обширных знаний, умений и навыков в решении линейных уравнений, преобразованию многочленов и алгебраических дробей. Для её понимания необходимы навыки в выполнении таких заданий, как: найти множество допустимых значений переменной, упростить дробное выражение. Необходимым также является четкое понимание невозможности деления на 0.

Всё это достигается путем пропедевтики на этапе изучения соответствующих тем в 5-8 классах, периодическим повторением перечисленных вопросов, отработкой нужных навыков. Перечисленные рекомендации призваны помочь в организации этой работы.

Во время изучения данной темы существует несколько подходов к решению и теоретическому обоснованию алгоритма решения, выбор правильного подхода влияет как на понимание данной темы, так и на восприятие последующих тем и алгоритмов.

Применение навыков решения уравнений с переменной в знаменателе не ограничивается рассмотренными темами, они применяются во многих разделах в процессе дальнейшего изучения предмета. Поэтому, в дальнейшем также необходимо периодически обращаться к этому вопросу с целью повторения.

Список литературы

Частная методика:

1. Методика преподавания математики в средней школе. /Под ред. Мишина В.И. - М.: Просвещение 1987. Талочкин П.Б. Неравенства и уравнения. - М.: Просвещение, 1970.

2. Колягин Ю.М., Луканкин Г.Л. «Основные понятия школьного курса математики» / Пособие для учителей. Под ред. А. И. Макушевича. М., «Просвещение» 1974.

3. Микракова Т.Н. «Развивающие задачи на уроках математики в 5 – 8 классах» / пособие для учителя, Журнал «Квантор», 1991

4. Черкасов Р.С. И др. «Методические разработки по методике преподавания математики в средней школе (4-8 классы)» / МГПИ им. Ленина, Москва 1980.

5. Брадис В.М. «Методика преподавания математики в средней школе» под ред. Маркушева А. И. / Москва, УЧПЕДГИЗ, 1954.

Учебники:

21. Дорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и др. «Математика 5» / Дрофа, 1996.

22. Истомина Н.Б. «Математика 5 класс» / изд. XXI-век, 2005.

23. Волович М.Б. «Математика 5» / Вентана-Граф; 2003.

24. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. «Математика 6». / Мнемозина, 1997

25. Дорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и др. «Математика 6» / Дрофа, 1996.

26. Истомина Н.Б. «Математика 6 класс» / изд. XXI-век, 2005.

27. Нурк Э.Р., Тельгмаа А.Э. «Математика 6» / Дрофа, 1996

28. «Алгебра»: Учеб. Для 7 кл. общеобразовательных учреждений / Под редакцией С.А. Теляковского - М: Просвещение, 2002.

29. Алимов Ш.А., Ю.М. Колягин, Ю.В. Сидоров и др. «Алгебра: Учеб. Для 7 кл.» / М: Просвещение, 1999.

30. Макарычев Ю.Н. «Алгебра 7 класс» / Просвещение, 2003.

31. «Алгебра»: Учеб. Для 8 кл. общеобразовательных учреждений / Под редакцией С.А. Теляковского - М: Просвещение, 2002.

32. Мордкович А.Г. и др. «Алгебра 8 класс» / Учебник для общеобразовательных учреждений - М: Мнемозина, 2002.

33. Алимов Ш.А., Ю.М. Колягин, Ю.В. Сидоров и др. «Алгебра: Учеб. Для 9 кл.» / М: Просвещение, 1999.

34. Мордкович А.Г. и др. «Алгебра 9 класс» / Учебник для общеобразовательных учреждений - М: Мнемозина, 2002.