Знаходження похідної функції
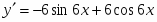
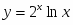
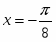
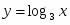
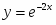
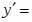
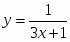
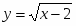
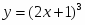
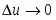 ТЕМА УРОКУ: Похідні елементарних функцій
ТЕМА УРОКУ: Похідні елементарних функцій
МЕТА УРОКУ: формування знань учнів про похідну сталої функції, степеневої функції з цілим показником, тригонометричних функцій.
І Перевірка домашнього завдання
1. Три учні відтворюють розв’язування вправ № 1 (1,2), 2.
1) 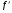 =
=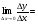
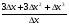 =
=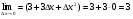
2) 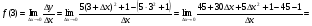
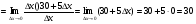
Рівняння шуканої дотичної у – у0 =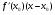 . Оскільки х0 = 1, у = х2, то
. Оскільки х0 = 1, у = х2, то 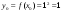 і
і 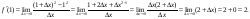
Отже, у – 1 = 2 (х -1) або у = 2х – 1.
2. Фронтальна бесіда за запитаннями №№ 11 – 17 із Запитання і завдання до розділу VII.
II. Сприймання і усвідомлення знань про похідну сталої функції, степеневої функції з цілим показником
На попередньому уроці ми довели, що похідна лінійної функції у = 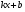 дорівнює
дорівнює 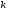 , тобто
, тобто 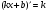 .
.
Якщо покласти 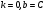 , де С – довільна постійна, то одержимо, що тобто похідна постійної функції дорівнює 0.
, де С – довільна постійна, то одержимо, що тобто похідна постійної функції дорівнює 0.
Якщо у формулі 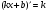 покласти
покласти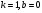 , то одержимо
, то одержимо
Нам уже відомо, що . А як знайти похідну функції у = х5, у = х20 тощо? Розглянемо функцію у= хn, де n – 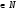 .
.
Знайдемо похідну цієї функції, для цього зафіксуємо значення аргумента х0 і надамо йому приросту 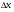 , тоді:
, тоді:
1) 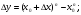
2) 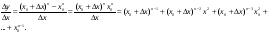
(Скориставшись формулою 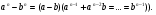
3) 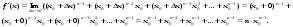
Звідси
Розглянемо функцію у = хn-1, де 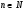 .
.
Знайдемо похідну цієї функції, для цього зафіксуємо значення аргумента х0 і надамо йому приросту 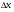 , тоді
, тоді
1) 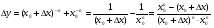
2) 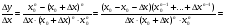
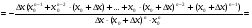
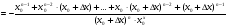
3) 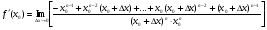 =
=
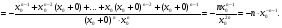
Отже, 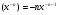 , де
, де 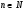 .
.
Таким чином виконується рівність: 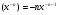 .
.
Виконання вправ
1. Знайдіть похідну функції:
а) у = х6; б) у = х8; в) у = х2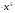 ; г)
; г) 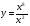 .
.
Відповідь: а) 6х5; б) 8х7; в) 7х6; г) 6х5.
2. Знайдіть похідні функцій:
а) у = х-10; б) у = х2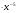 ; в)
; в) 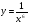 ; г)
; г)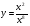 .
.
Відповідь: а) -10х-11; б) -3х-4; в) -6х-7; г) -6х-7.
ІІІ. Сприймання і усвідомлення знань про похідну тригонометричних функцій
Знайдемо похідну функції у=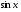 . Зафіксуємо х0 і надамо аргументу приросту
. Зафіксуємо х0 і надамо аргументу приросту 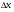 , тоді:
, тоді:
1) 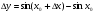
2) 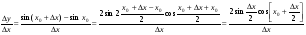
3) 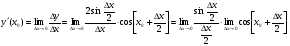
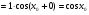 .
.
Отже
Аналогічно можна довести, що
Знайдемо похідну функції 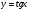 .
.
Зафіксуємо х0 і надамо аргументу приросту 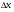 , тоді:
, тоді:
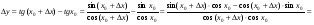
 .
.
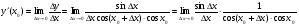
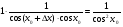 .
.
Отже,
Аналогічно можна довести, що
Виконання вправ № 1 (3), 5 із підручника.
VI. Підведення підсумків уроку
Провести підведення підсумків уроку з використанням таблиці 4 похідних.
Таблиця
Таблиця похідних
(хn)=n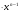 ;
; 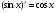 ;
;
(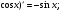
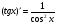 ;
;
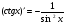 ;
; 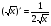 .
.
V. Домашнє завдання
Розділ VІІ § 3. запитання і завдання для повторення розділу VІІ № 19 – 22. вправа №4 (2, 4).
ТЕМА УРОКУ: Теореми про похідну суми, добутку і частки функцій
МЕТА УРОКУ: Вивчення теореми про похідні суми, добутку і частки функцій, формування умінь учнів у знаходження похідних.
І. Перевірка домашнього завдання
1. Усне розв’язування вправ.
1) Знайдіть похідні функцій
а) у – х10; б) 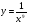 ; в)
; в) 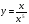 ; г)
; г) 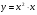 .
.
Відповідь: а) 10х9; б) -9х-10; в) -4х-5;ё г) 3х2.
2) Знайдіть похідні функцій:
а) 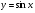 в точці
в точці 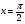 ; б)
; б) 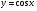 в точці
в точці 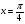 ;
;
в) 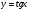 в точці
в точці 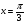 ; г)
; г) 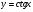 в точці
в точці 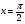 .
.
Відповідь: а) 0; б) 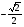 ; в) 4; г) -1.
; в) 4; г) -1.
2. Відповісти на запитання, що виникли у учнів під час виконання домашніх вправ.
ІІ. Сприймання і усвідомлення теореми про похідну суми функції
Теорема: Якщо функції f(x) і g(x) диференційовані в точці х, то їхня сума диференційована в цій точці і
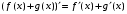
або коротко говорять: похідна суми дорівнює сумі похідних.
Доведення
Розглянемо функцію  у = f(x) + g(x).
у = f(x) + g(x).
Зафіксуємо х0 і надамо аргументу приросту 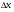 . Тоді
. Тоді
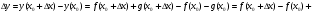
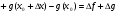 ,
,
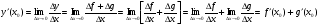 .
.
Отже, 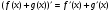 .
.
Наслідки
а) Похідна різниці дорівнює різниці похідних.
Нехай у(х) = f(x) - g(x), тоді f(x) = у(х) + g(x) і 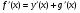 , звідси
, звідси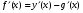 .
.
б) Похідна суми декількох функцій дорівнює сумі похідних цих фукцій, тобто
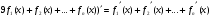 .
.
Приклад. Знайдіть похідну функцій
а) 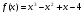 ;
;
б) 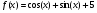 ;
;
в) 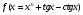 .
.
Розв’язання а) 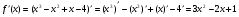 ;
;
б) 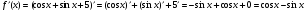 .
.
в)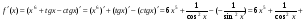
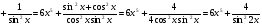 .
.
Відповідь: а) 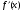
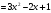 ; б)
; б) 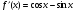 в)
в) 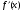 =
=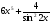 .
.
Виконання вправ
1. Знайдіть похідні функцій:
а) у = х3 + х – х4; б) 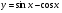 ;
;
в) 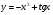 ; г)
; г) 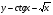 .
.
Відповідь: а)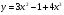 ; б)
; б)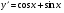 ; в)
; в) 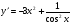 ;
;
г) 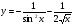 .
.
2. Знайдіть значення похідної функції f(x) в точці х0:
а) 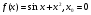 ;
;
б) 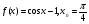 ;
;
в) 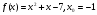 .
.
Відповідь: а) 1; б) 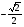 ; в)-1.
; в)-1.
3. При яких значеннях х значення похідної функції f(x) дорівнює 0:
а)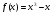 ; б)
; б) 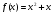 ; в)
; в) 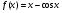 .
.
Відповідь: а) 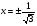 ; б)
; б) 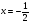 ; в)
; в) 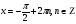 .
.
ІІІ. Сприймання і усвідомлення теореми про похідну добутку
Теорема. Якщо функції f(x) і g(x) диференційовані в точці х, то їхній добуток також – диференційована функція в цій точці і 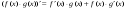 , або коротко говорять: похідна добутку двох функцій дорівнює сумі добутків кожної функції на похідну другої функції
, або коротко говорять: похідна добутку двох функцій дорівнює сумі добутків кожної функції на похідну другої функції
Доведення. Розглянемо функцію 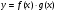 . Зафіксуємо х0 і надамо аргументу приросту
. Зафіксуємо х0 і надамо аргументу приросту 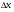 , тоді
, тоді
1) 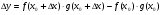
Оскільки 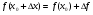 ,
, 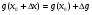 , то
, то
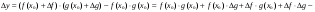
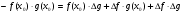 .
.
2) 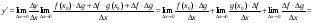
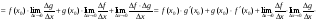
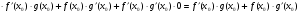 .
.
Отже, 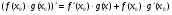 .
.
Наслідки
а) Постійний множник можна винести за знак похідної: 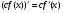 .
.
Дійсно,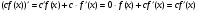 .
.
б) Похідна добутку декількох множників дорівнює сумі добутків похідної кожного із них на всі останні, наприклад:
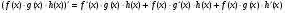 .
.
Приклад. Знайдіть похідні функцій:
а) 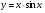 ;
;
б) 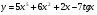 ;
;
в) 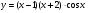 .
.
Розв’язування
а) 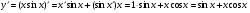 ;
;
б) 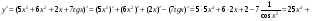
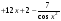 ;
;
в) 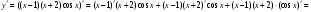
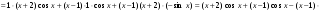
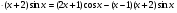 .
.
Виконання вправ.
1. Знайдіть похідну функцій:
а) 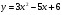 ; б)
; б) 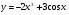 ;
;
в) 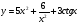 ; г)
; г) 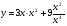 .
.
Відповідь: а) 6х-5; б) 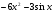 ;
;
в) 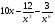 ; г)
; г) 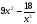 .
.
2. Знайдіть похідні функцій:
а) 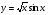 ; б)
; б) 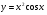 ;
;
в) 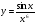 ; г)
; г) 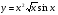 .
.
Відповідь: а) 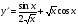 ; б)
; б) 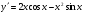 ;
;
в) 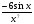 ; г)
; г) 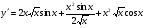 .
.
3. Знайдіть похідні функцій:
а) 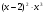 ; б)
; б) 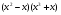 .
.
Відповідь: а) 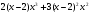 ; б)
; б) 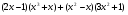 .
.
IV. Сприймання і усвідомлення теореми про похідну частки функцій
Теорема. Якщо функції f(x) і g(x) диференційовані в точці х і g(x)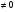 , то функція
, то функція 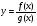 диференційована в цій точці і
диференційована в цій точці і 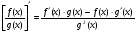 .
.
Доведення
Формулу похідної частки можна вивести, скориставшись означенням похідної. Проте це зробити можна простіше.
Нехай 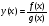 , тоді f(x)=у(х)
, тоді f(x)=у(х)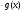 . Знайдемо похідну функції f(x), скориставшись теоремою про похідну добутку,
. Знайдемо похідну функції f(x), скориставшись теоремою про похідну добутку, 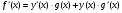 . Виразимо з цієї формули
. Виразимо з цієї формули 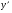
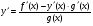
і підставимо замість у(х) значення 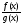 , тоді будемо мати:
, тоді будемо мати:
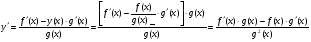 .
.
Отже, 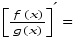
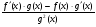 .
.
Приклад: Знайдіть похідні функцій
а) 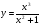 ; б)
; б) 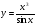 .
.
Розв’язання
а) 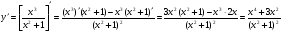 .
.
б) 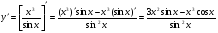 .
.
Виконання вправ
1. Знайдіть похідні функцій:
а) 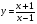 ; б)
; б) 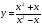 ; в)
; в) 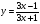 ; г)
; г) 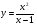 .
.
Відповідь: а) 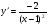 ; б)
; б) 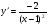 ;
;
в) 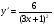 ; г)
; г) 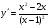 .
.
2. Знайдіть похідні функцій:
а) 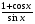 ; б)
; б) 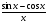 ; в)
; в) 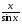 ; г)
; г) 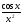
Відповідь: а) 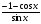 ; б)
; б) 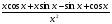 ;
;
в) 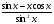 ; г)
; г) 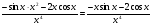 .
.
V. Домашнє завдання
Розділ VII § 4. Запитання і завдання для повторення розділу VII № 23 – 27. вправа № 10 (1 -5, 7 - 8).
ТЕМА УРОКУ: Похідна складеної функції
Мета уроку: Формування поняття про похідну складеної функції, знань учнів про похідну складеної функції, умінь знаходити похідну складеної функції.
І. Перевірка домашнього завдання
1) 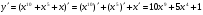 ;
;
2) 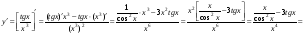
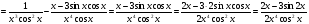 ;
;
3) 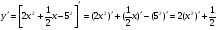
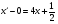 ;
;
4) 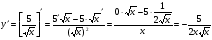 ;
;
5) 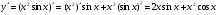 ;
;
6) 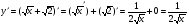 .
.
2. Самостійна робота.
Варіант 1.
1. Знайдіть значення похідної функції f(x) при заданому значенні аргументу х0:
а) 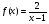 , х0=-1. (2 бали)
, х0=-1. (2 бали)
б) 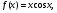
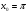 . (2 бали)
. (2 бали)
2. Знайдіть похідну функцій:
а) 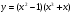 . (2 бали)
. (2 бали)
б) 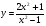 . (2 бали)
. (2 бали)
в) 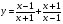 . 42 бали)
. 42 бали)
Варіант 2.
1. Знайдіть значення похідної функції f(x) при заданому значенні аргумента х0:
а) 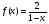 , х0=-1. (2 бали)
, х0=-1. (2 бали)
б) 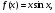
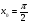 . (2 бали)
. (2 бали)
2. Знайдіть похідну функцій:
а) 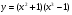 . (2 бали)
. (2 бали)
б) 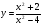 . (2 бали)
. (2 бали)
в) 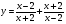 . 42 бали)
. 42 бали)
Відповідь: В-1. 1. а) 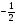 ; б) -1
; б) -1
2. а) 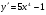 ; б)
; б) 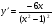 ; в)
; в) 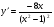
В-2. 1. а) 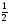 ; б) 1
; б) 1
2. а) 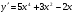 ; б)
; б) 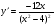 ; в)
; в) 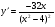 .
.
ІІ. Сприймання і усвідомлення поняття складеної функції та її похідної
Розглянемо приклад.
Приклад 1. Нехай треба обчислити по заданому значенню х значення функції у, яка задана формулою 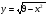 .
.
Для цього спочатку треба обчислити за даним значенням х значення u=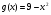 , а потім за значенням u обчислити у=
, а потім за значенням u обчислити у=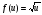 .
.
Отже, функція g ставить у відповідність числу х число u, а функція f – числу u число у. Говорять, що у є складеною функцією із функції g і f, і пишуть 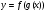 .
.
Функцію g(х) називають внутрішньою функцією, або проміжною змінною, функцію f(u) – зовнішньою функцією. Отже, щоб обчислити значення складеної функції 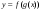 в довільній точці х, спочатку обчислюють значення u внутрішньої функції g, а потім f(u).
в довільній точці х, спочатку обчислюють значення u внутрішньої функції g, а потім f(u).
Приклад 2. Розглянемо функцію 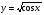 . Вона є складною із функцій
. Вона є складною із функцій 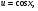
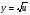 , де
, де 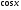 - внутрішня функція,
- внутрішня функція, 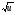 - зовнішня функція.
- зовнішня функція.
Приклад 3. Запишіть складні функції 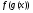 і
і 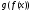 , якщо
, якщо 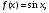
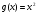
Розв’язання
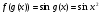
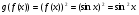
Виконання вправ.
1. Задайте формулою елементарні функції 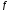 і
і 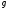 , із яких побудована складна функція
, із яких побудована складна функція 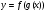 :
:
а)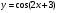 б)
б) 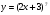
в)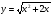 г)
г) 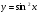
Відповіді: а) 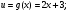
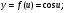
б) 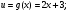
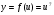 ;
;
в) 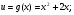
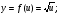
г) 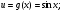
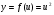 .
.
2. Дано функції: 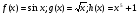 . Побудуйте функції:
. Побудуйте функції:
а) 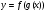 ; в)
; в) 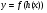 ; в)
; в) 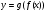 ;
;
г) 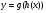 ; в)
; в) 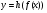 ; є)
; є) 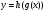 .
.
Відповідь: а) 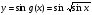 ; б)
; б) 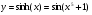 ;
;
в) 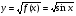 ; г)
; г) 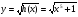 ;
;
д) 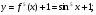 є)
є) 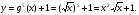
У складній функції 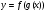 присутня проміжна змінна
присутня проміжна змінна 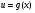 . Тому при знаходженні похідної складної функції ми будемо вказувати, по якій змінній взято похідну, використовуючи при цьому спеціальні показники:
. Тому при знаходженні похідної складної функції ми будемо вказувати, по якій змінній взято похідну, використовуючи при цьому спеціальні показники:
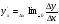 – похідна функції у по аргументі х;
– похідна функції у по аргументі х;
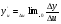 – похідна функції у по аргументі u;
– похідна функції у по аргументі u;
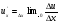 – похідна функції u по аргументі х;
– похідна функції u по аргументі х;
Теорема. Похідна складеної функції 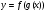 знаходиться за формулою
знаходиться за формулою 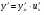 , де
, де 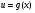 , або похідна складеної функції дорівнює похідній зовнішньої функції по проміжній змінній, помноженій на похідну внутрішньої функції по основному аргументу.
, або похідна складеної функції дорівнює похідній зовнішньої функції по проміжній змінній, помноженій на похідну внутрішньої функції по основному аргументу.
Доведення
Будемо вважати, що функція 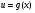 має похідну в точці х0, а функція
має похідну в точці х0, а функція 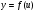 має похідну в точці u0=
має похідну в точці u0=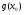 , тобто існують границі
, тобто існують границі 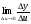 ,
, 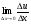 і
і 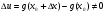 .
.
Нехай, аргументу х0 надано приросту 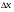 , тоді змінна u набуде приросту
, тоді змінна u набуде приросту 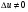 . Поскільки
. Поскільки 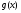 одержала приріст
одержала приріст 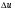 , то функція у одержить також приріст
, то функція у одержить також приріст 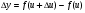 . Приріст
. Приріст 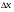 зумовив виникнення приросту
зумовив виникнення приросту 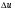 і
і 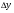 .
.
Подамо 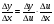 . Перейдемо до границі при
. Перейдемо до границі при 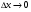 (при цьому ).
(при цьому ).
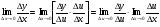 або
або 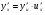 .
.
Приклад 1. Знайдіть похідну функції у = (3х3-1)5.
Розв’язання
у = (3х3-1)5 – складена функція 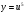 , де u =3х3-1, тоді
, де u =3х3-1, тоді 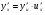 ,
, 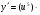
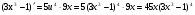 .
.
При обчисленні похідної складеної функції явне введення допоміжної букви u для позначення проміжного аргументу не є обов’язковим. Тому похідну даної функції знаходять відразу як добуток похідної степеневої функції u5 на похідну від функції 3х3-1:
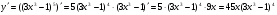 .
.
Приклад 2.Знайдіть похідні функцій:
а) 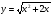 ; б)
; б) 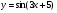 ;
;
в) 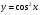 ; г)
; г) 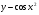 .
.
Розв’язання
а) 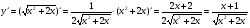 ;
;
б) 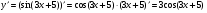 ;
;
в) 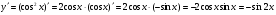 ;
;
г) 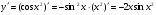 .
.
Виконання вправ.
1. знайдіть похідні функцій:
а) у = (3х+2)50; б) (6-7х)10;
в) 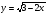 ; г)
; г) 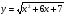 .
.
Відповідь: а) 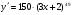 ; б)
; б) 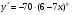 ;
;
в) 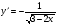 ; г)
; г) 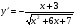 .
.
2. Знайдіть похідні функцій:
а) 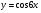 ; б)
; б) 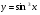 ;
;
в) 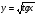 ; г)
; г) 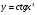 .
.
Відповідь: а) 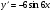 ; б)
; б) 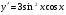 ;
;
в) 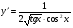 ; г)
; г) 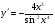 .
.
ІІІ. Підведення підсумків уроку
При підведенні підсумків уроку можна скористатись таблицею.
Таблиця диференціювання
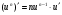
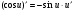
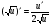
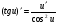
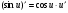
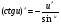
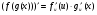 ,де
,де 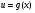
IV. Домашнє завдання
Розділ VII § 4. запитання і завдання для повторення до розділу VII № 23–28. вправа № 10 (6, 10, 14, 22).
ТЕМА УРОКУ: Похідна показникової, логарифмічної та степеневої функцій
Мета уроку: Формування знань учнів про похідну показникової, логарифмічної та степеневої функції(з довільним дійсним показником), умінь учнів в знаходженні похідних функцій.
І. Перевірка домашнього завдання
1.Перевірити правильність виконання домашніх вправ за записами, зробленими на дошці.
6) 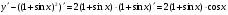 ;
;
10) 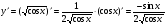 ;
;
11) 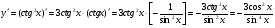 ;
;
22) 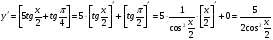 .
.
2. Виконання усних вправ.
Знайдіть похідні функцій, які подано в таблиці.
Таблиця
1
2
3
4
1
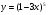
2

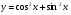
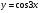
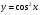
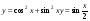
3
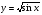
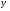 =
=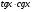
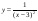
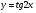
4
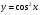
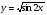
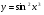
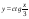
ІІ. Сприймання і усвідомлення матеріалу про похідну показникової функції
Перш ніж знаходити похідну показниковїх функції, зробимо два важливих зауваження. Графік функції у=ах проходить через точку (0; 1). Нехай 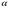 – величина кута , утвореного дотичною до графіка функції у = ах в точці (0; 1)з додатним напрямом осі абсцис. Величина цього кута залежить від значення основи а. Наприклад, обчислено, що при а = 2 величина кута
– величина кута , утвореного дотичною до графіка функції у = ах в точці (0; 1)з додатним напрямом осі абсцис. Величина цього кута залежить від значення основи а. Наприклад, обчислено, що при а = 2 величина кута 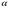 приблизно дорівнює 340(рис.29), а при а = 2,
приблизно дорівнює 340(рис.29), а при а = 2, 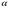 =470.
=470.
у у = ех якщо основа а показникової функції у = ах зростає від 2 до 3, то величина кута 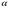 зростає і приймає значення від 340 до 470. Отже, існує таке значення
зростає і приймає значення від 340 до 470. Отже, існує таке значення 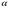 , при якому дотична, проведена до графіка функції у = ах в точці (0; 1) утворює з додатним напрямком осі ОХ кут 450 (рис.31). Таке значення
, при якому дотична, проведена до графіка функції у = ах в точці (0; 1) утворює з додатним напрямком осі ОХ кут 450 (рис.31). Таке значення 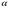 прийнято позначати буквою е, е – число ірраціональне, е = 2,718281828459...
прийнято позначати буквою е, е – число ірраціональне, е = 2,718281828459... 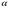 0
0
Таким чином, дотична до графіка функції у = ех в точці (0; 1) утворює з додатним напрямком осі абсцис, який дорівнює 450.
У відповідності з геометричним змістом похідної даний висновок означає, що значення похідної функції 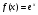 в точці х0 дорівнює
в точці х0 дорівнює 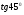 =1. Отже,
=1. Отже, 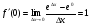 .
.
Знайдемо тепер формулу похідної функції 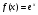 .
.
Нехай аргумент х0 одержав приріст 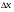 , тоді:
, тоді:
1) 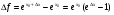
2) 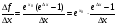
3) 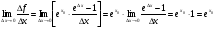 .
.
Таким чином, похідна функції ех дорівнює самій функції: 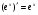
Знайдемо похідну функції 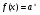 , скориставшись основною логарифмічною тотожністю та правилом знаходження похідної складеної функції:
, скориставшись основною логарифмічною тотожністю та правилом знаходження похідної складеної функції:
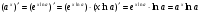 .
.
Отже, 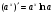
Похідна показникової функції дорівнює добутку цієї функції на натуральний логарифм її основи.
Приклад 1. Знайдіть похідну функцій:
а) у = 5х; б) у = е3-2х; в) 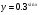 ; г)
; г) 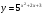 .
.
Розв’язання
а) 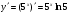 ;
;
б) 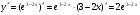 ;
;
в) 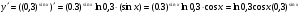 ;
;
г) 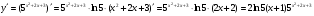 .
.
Виконання вправ.
№ 2 (2, 4, 6, 8, 10, 12), №2 (20, 22, 24, 26, 28, 30) із підручника (розділ Х).
ІІІ. Сприймання і усвідомлення матеріалу про похідну логарифмічної функції
Розглянемо функцію 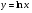 . За основною логарифмічною тотожністю:
. За основною логарифмічною тотожністю: 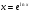 для всіх додатних х.
для всіх додатних х.
Диференціюючи обидві частини цієї рівності, одержимо: 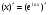 , або
, або 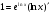 .
.
Звідси 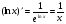 .
.
Отже,
Знайдемо похідну функції 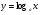 . Так як
. Так як 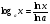 , то
, то
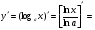
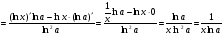 .
.
Отже,
Приклад 1. Знайдіть похідну функцій:
а) 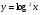 ; б)
; б) 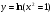 ;
;
в) 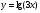 ; г)
; г) 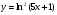 .
.
а) 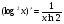 ;
;
б) 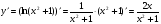 ;
;
в) 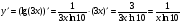 ;
;
г) 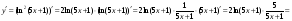
=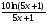 .
.
Виконання вправ.
№ 2 (14, 16, 18, 32, 34, 36, 38, 40, 42), із підручника (розділ Х).
IV. Сприймання і усвідомлення матеріалу про похідну степеневої функції 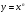 , де
, де 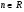
Ми довели, що 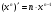 для
для 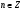 .
.
Розглянемо функцію 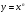 , де
, де 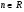 .
.
Знайдемо похідну цієї функції:
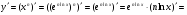
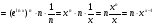 .
.
Отже, 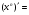
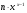 для всіх
для всіх 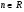 .
.
ТЕМА УРОКУ: Розв’язування вправ
Мета уроку: Формування умінь учнів знаходити похідні функцій.
І. Перевірка домашнього завдання
1 перевірити правильність виконання домашніх вправ шляхом порівняння відповідей.
№ 2. 3) -е-х; 5) 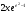 ; 7)
; 7) 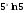 ; 9)
; 9) 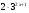 ; 11)
; 11) 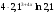
13) 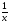 ; 15)
; 15) 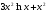
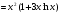 ; 17)
; 17) 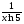 .
.
№ 8. 1) 100х99; 3) 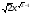 ; 5)
; 5) 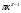 ; 7) -20х19; 9)
; 7) -20х19; 9) 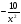 ;
;
11) 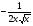 .
.
2. Усне розв’язування вправ.
Знайдіть похідні функцій, поданих в таблиці.
1
2
3
4
5
1
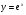
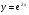
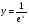
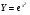
2
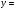
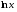
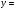
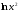
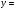
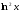
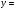
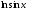
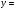
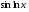
3
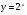
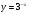
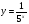
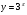
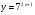
4
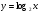
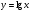
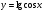
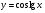
5
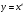
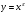
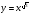
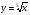
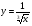
ІІ. Формування умінь знаходити похідні функцій
Виконання вправ № 10 (12; 11; 13; 17; 19) розділу VІІ підручника.
Виконання вправ № 2 (23; 24; 31; 34; 35; 36) розділу Х підручника.
Знайдіть похідну функції
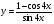 та обчисліть її значення, якщо .
та обчисліть її значення, якщо .

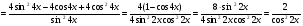 .
.
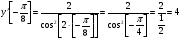 .
.
Відповідь: 4.
4) Тіло рухається за законом 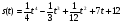 .
.
Знайдіть швидкість точки через 2 секунди після початку руху. (Відстань вимірюється в метрах).
Розв’язання
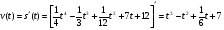 ;
;

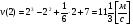 .
.
Відповідь: 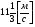 .
.
ІІІ. Домашнє завдання
Підготуватися до контрольної роботи. Вправи ; 10 (15; 16; 20; 25) розділу VІІ; № 2 (22; 26; 38; 42), 8 (14; 18) розділу Х.
ТЕМА УРОКУ: Тематична контрольна робота № 1
Мета уроку: Перевірити навчальні досягнення учнів з теми „Границя, неперервність та похідна функцій”.
Варіант 1
1. Знайдіть похідну функції:
а) 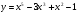 . (2 бали)
. (2 бали)
б) 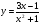 . (2 бали)
. (2 бали)
в) 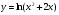 . (2 бали)
. (2 бали)
г) 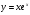 . (2 бали)
. (2 бали)
2. Знайдіть похідну функції 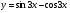 та обчислити її значення, якщо
та обчислити її значення, якщо 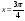 . (2 бали)
. (2 бали)
3. Точка рухається за законом 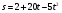 . Знайдіть миттєву швидкість точки моменту t=1 с (s вимірюється в метрах). (2бали)
. Знайдіть миттєву швидкість точки моменту t=1 с (s вимірюється в метрах). (2бали)
Варіант 2
1. Знайдіть похідну функції:
а) 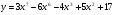 . (2 бали)
. (2 бали)
б) 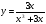 . (2 бали)
. (2 бали)
в) 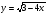 . (2 бали)
. (2 бали)
г) 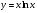 . (2 бали)
. (2 бали)
2. Знайдіть похідну функції 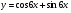 та обчислити її значення, якщо
та обчислити її значення, якщо 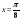 . (2 бали)
. (2 бали)
3. Точка рухається за законом 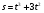 . Знайдіть миттєву швидкість точки моменту t=1 с (s вимірюється в метрах). (2бали)
. Знайдіть миттєву швидкість точки моменту t=1 с (s вимірюється в метрах). (2бали)
Варіант 3
1. Знайдіть похідну функції:
а) 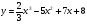 . (2 бали)
. (2 бали)
б) 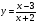 . (2 бали)
. (2 бали)
в) 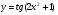 . (2 бали)
. (2 бали)
г) . (2 бали)
2. Знайдіть похідну функції 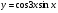 та обчислити її значення, якщо
та обчислити її значення, якщо 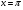 . (2 бали)
. (2 бали)
3. Точка рухається за законом 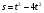 . Знайдіть миттєву швидкість точки моменту t=5 с (s вимірюється в метрах). (2бали)
. Знайдіть миттєву швидкість точки моменту t=5 с (s вимірюється в метрах). (2бали)
Варіант 4
1. Знайдіть похідну функції:
а) 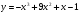 . (2 бали)
. (2 бали)
б) 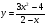 . (2 бали)
. (2 бали)
в) 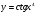 . (2 бали)
. (2 бали)
г)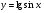 . (2 бали)
. (2 бали)
2. Знайдіть похідну функції 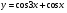 та обчислити її значення, якщо
та обчислити її значення, якщо 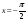 . (2 бали)
. (2 бали)
3. обертання тіла навколо осі здійснюється за законом 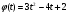 . Знайдіть кутову швидкість точки при t=4 с (
. Знайдіть кутову швидкість точки при t=4 с (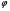 вимірюється в радіанах). (2бали)
вимірюється в радіанах). (2бали)
Відповідь: В-1. 1. а) 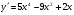 ; б)
; б) 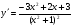 ;
;
в) 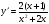 ,; г)
,; г) 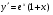 .
.
2. 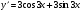 ,
, 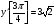 .
.
3. 10 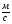
В-2 1. а) 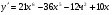 ; б)
; б) 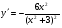 ;
;
в) 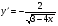 ,; г)
,; г) 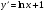 .
.
2. , 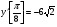 .
.
3. 9 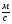
В-3. 1. а) 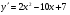 ; б)
; б) 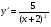 ;
;
в) 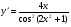 ,; г)
,; г) 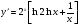 .
.
2. 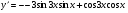 ,
, 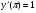 .
.
3. 35 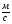
В-4. 1. а) 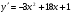 ; б)
; б) 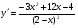 ;
;
в) 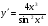 ,; г)
,; г) 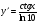 .
.
2. 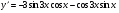 ,
, 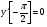 .
.
3. 20 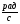

Нравится материал? Поддержи автора!
Ещё документы из категории педагогика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ