Расчет параметров идеального газового потока в камере ракетного двигателя
Агентство по образованию Российской Федерации Самарский Государственный Аэрокосмический Университет имени академика С.П. Королева
(Национальный исследовательский университет)
Кафедра теплотехники и тепловых двигателей
Расчетно-пояснительная записка к курсовой работе:
«РАСЧЕТ ПАРАМЕТРОВ ИДЕАЛЬНОГО ГАЗОВОГО ПОТОКА В КАМЕРЕ РАКЕТНОГО ДВИГАТЕЛЯ»
по дисциплине «Механика жидкостей и газов»
Вариант №13
Выполнил:
студент гр. 2301
Клипиков Н.Ю.
Проверил:
к.т.н. Диденко А. А.
Самара 2010
РЕФЕРАТ
Курсовая работа.
Пояснительная записка: 50 стр., 5 рис., 4 таблиц, 3 приложения, 3 источника.
Графическая документация: 1 лист формата A3.
КАНАЛ ПЕРЕМЕННОГО СЕЧЕНИЯ, ПРОФИЛЬ СВЕРХЗВУКОВОГО СОПЛА, КРИТИЧЕСКОЕ СЕЧЕНИЕ, СОПЛО ЛАВАЛЯ, ДАВЛЕНИЕ, ТЕМПЕРАТУРА, СКОРОСТЬ, РАСХОД, ПРЯМОЙ СКАЧОК УПЛОТНЕНИЯ, СТРУЯ ГАЗА, РАДИУС СЕЧЕНИЯ СОПЛА, ГАЗОВЫЙ ПОТОК, ДОЗВУКОВОЕ ТЕЧЕНИЕ ГАЗА, ИДЕАЛЬНЫЙ ГАЗ.
В данной курсовой работе выполнены расчеты геометрических параметров камеры ракетного двигателя, параметров идеального газового потока в камере ракетного двигателя, схема которого представлена в приложении, построены графики изменения основных величин.
Газовый поток поступает в сверхзвуковое сопло с начальным сечением 0, узким сечением у, выходным сечением a, площади которых равны соответственно S0, Sу, Sa. Из сопла газ вытекает во внешнюю среду, давление в которой равно 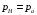 (исходная постановка задачи) .
(исходная постановка задачи) .
ЗАДАНИЕ
Заданы следующие величины параметров:
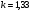 - отношение теплоемкости газа при постоянном давлении к его теплоемкости при постоянном объеме .
- отношение теплоемкости газа при постоянном давлении к его теплоемкости при постоянном объеме .
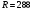 - удельная газовая постоянная .
- удельная газовая постоянная .
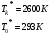 - температуры торможения газового потока при втекании ее в камеру сгорания и в конце ее (перед соплом) .
- температуры торможения газового потока при втекании ее в камеру сгорания и в конце ее (перед соплом) .
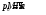 - давление в газовом потоке в сечении 0 .
- давление в газовом потоке в сечении 0 .
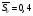 - отношение площадей
- отношение площадей 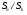 .
.
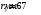 - радиус узкого сечения сопла .
- радиус узкого сечения сопла .
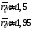 - отношение радиусов камеры сгорания
- отношение радиусов камеры сгорания 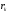 и выходного сечения сопла
и выходного сечения сопла 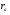 к радиусу
к радиусу 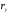 .
.
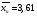 - отношение длины сверхзвуковой части сопла
- отношение длины сверхзвуковой части сопла 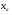 к радиусу
к радиусу 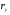 .
.
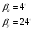 - углы между касательными к профилю сопла в узком и выходном сечениях и осью сопла .
- углы между касательными к профилю сопла в узком и выходном сечениях и осью сопла .
Газ идеальный, невязкий. Течение газа в сопле сплошное, стационарное, энергоизолированное. Расход в каждом сечении одинаковый. В сечении 0 – дозвуковой газовый поток. Скачок уплотнения в газовом потоке прямой и энергоизолированный. Из канала газовый поток вытекает в окружающую среду с давлением равным давлению наружному (pa=pн). Живые сечения считать плоскими сечениями, нормальными оси потока (оси сопла).
Рассчитываемые режимы газового потока
В курсовой работе рассчитываются следующие режимы идеального потока в сверхзвуковом сопле:
1) Расчетный режим течения газа, соответствующий сверхзвуковому соплу (соплу Лаваля).
2) Нерасчетный режим течения газа, соответствующий сверхзвуковому соплу со скачком уплотнения в выходном сечении a.
3) Нерасчетный режим течения газа, соответствующий сверхзвуковому соплу со скачком уплотнения в сечении 5.
4) Нерасчетный режим течения газа, соответствующий сверхзвуковому соплу со скачком уплотнения в сечении 4.
5) Дозвуковое течение газа по всему каналу, но при критическом состоянии газового потока в узком сечении (λу= 1).
Содержание
ИСПОЛЬЗОВАННЫЕ СИМВОЛЫ
r – радиус, мм
S – площадь, мм2
q – газодинамическая функция расхода или приведенный расход
λ – приведенная скорость
M – число Маха
τ – ГДФ температуры
π – ГДФ давления
– ГДФ плотности
T* – температура торможения, К
T – статическая температура, К
p* – давление торможения, Па
p – статическое давление, Па
ρ* – плотность торможения, кг/м3
ρ – статическая плотность, кг/м3
aкр – критическая скорость звука, м/с
a – местная скорость звука, м/с
c – скорость газового потока, м/с
G – расход газового потока, кг/с
ƒ – ГДФ импульса
pн – давление во внешней среде, Па
Ф – импульс газового потока, Н
σп – коэффициент изменения давления в прямом скачке уплотнения
σв.р. – коэффициент изменения давления при внезапном расширении
σТ – коэффициент изменения давления при подводе теплоты
P0-у – сила воздействия газового потока на дозвуковую часть сопла, Н
Pу-a – сила воздействия газового потока на сверхзвуковую часть сопла, Н
P0-a – сила воздействия газового потока на сопло в целом, Н
Pвнут. – внутренняя составляющая полной тяги, Н
Pнар. – наружная составляющая полной тяги, Н
P – полная тяга двигателя, Н
1. Построение профиля камеры ракетного двигателя.
Рассчитаем значения параметров ракетного двигателя с помощью исходных данных:
1) длина камеры сгорания:
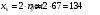 ,
,
2) длина дозвуковой части сопла:
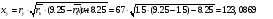 ,
,
3) длина сверхзвуковой части сопла:
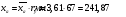 ,
,
4) радиус камеры сгорания:
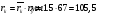 ,
,
5) радиус газового потока при входе в камеру сгорания:
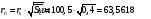 ,
,
6) радиус выходного сечения сопла:
 ,
,
7) характерные расстояния сечений 1, 2, 3, 4, 5 соответственно:
x1=0.35∙ xк=0.35∙134=46,9 мм;
x2=0.5∙ xу=0.5∙123,0869=61,5435 мм;
x3=0.2∙ xу=0.2∙123,0869=24,6174 мм;
x4=0.2∙ xa=0.2∙241,87=48,3740 мм;
x5=0.6∙ xa=0.6∙241,87=145,122 мм.
По рассчитанным параметрам построим профиль камеры сгорания см. приложение. По профилю камеры определяем радиусы промежуточных расчётных сечений r2, r3, r4, r5:
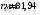 ,
, 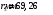 ,
, 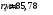 ,
, 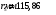 .
.
Рассчитываем площади всех сечений по формуле:
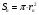
где  – радиус характерного сечения, мм:
– радиус характерного сечения, мм:

2. Расчёт первого варианта газового потока.
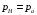 (
(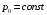 ).
).
Рассчитаем параметры потока при сверхзвуковом истечении газа из сопла.
1)Рассчитаем параметры газового потока для сечения «к»:
Приведенный расход для данного сечения:
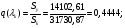
С использованием математического пакета MathCAD определяем величину 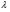 k из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении дозвуковой поток, т. е.
k из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении дозвуковой поток, т. е. 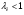 :
:
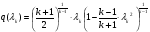 ,
,
получаем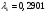 ;
;
Газодинамические функции определяем по формулам:
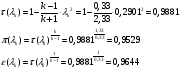
где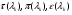 - газодинамические функции температуры, давления и плотности соответственно.
- газодинамические функции температуры, давления и плотности соответственно.
Найдём число Маха:
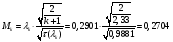
Определение параметров газового потока:
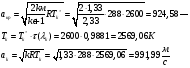
где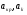 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 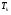 - статическая температура
- статическая температура
Найдем скорость газового потока:
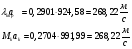
2) Рассчитаем параметры газового потока для сечения «0»:
С использованием математического пакета MathCAD определяем величину 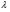 0 из решения преобразованного уравнения количества движения для газа (см. приложение 3), находящегося в камере сгорания между сечениями «0» и «k»), учитывая, что в данном сечении дозвуковой поток, т. е.
0 из решения преобразованного уравнения количества движения для газа (см. приложение 3), находящегося в камере сгорания между сечениями «0» и «k»), учитывая, что в данном сечении дозвуковой поток, т. е. 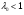 :
:
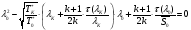 ,
,
получаем 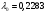 .
.
Газодинамические функции определяем по формулам:
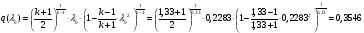

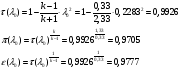
где 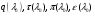 - газодинамические функции расхода, температуры, давления и плотности соответственно.
- газодинамические функции расхода, температуры, давления и плотности соответственно.
Найдём число Маха:
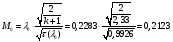
Определение параметров газового потока:
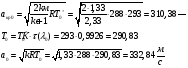
где 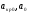 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 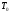 - статическая температура
- статическая температура
Найдем скорость газового потока:
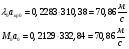
Найдём давление и плотность торможения:
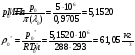
Определим недостающие параметры газового потока:
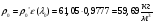
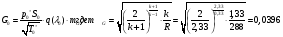
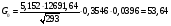
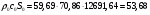
где 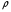 0– статическая плотность,
0– статическая плотность,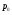 - статическое давление, а
- статическое давление, а 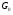 – расход газового потока
– расход газового потока
3) Вычислим оставшиеся параметры газового потока в сечении «k»:
Найдем значение давления из преобразованного уравнения неразрывности для живых сечений «0» и «k» газового потока: 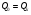 ;
;
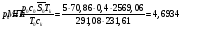
Найдём давление и плотность торможения:
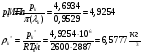
Определим недостающие параметры газового потока:
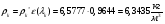
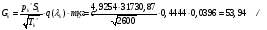
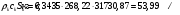
где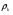 – статическая плотность,
– статическая плотность,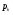 - статическое давление, а
- статическое давление, а 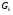 – расход газового потока
– расход газового потока
4) Рассчитаем параметры газового потока для сечения «1»:
Найдем λ1 через дискриминант
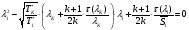 , где
, где  ;
;
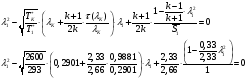
Получаем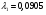 .
.
Газодинамические функции определяем по формулам:
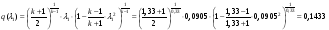
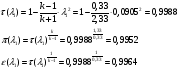
где 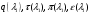 - газодинамические функции расхода, температуры, давления и плотности соответственно.
- газодинамические функции расхода, температуры, давления и плотности соответственно.
Найдём число Маха:
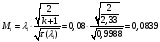
Определение параметров газового потока:
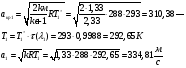
где 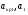 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 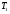 - статическая температура
- статическая температура
Найдем скорость газового потока:
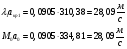
Найдем значение p1 из решения преобразованного уравнения неразрывности:
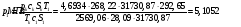
Найдём давление и плотность торможения:
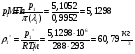
Определим недостающие параметры газового потока:
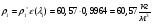
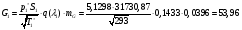
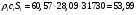
где 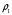 – статическая плотность,
– статическая плотность,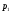 - статическое давление, а
- статическое давление, а 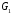 – расход газового потока
– расход газового потока
5)Рассчитаем параметры газового потока для сечения «2»:
Приведенный расход для данного сечения:
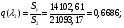
С использованием математического пакета MathCAD определяем величину  из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении дозвуковой поток, т. е.
из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении дозвуковой поток, т. е. 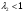 :
:
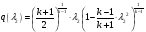 ,
,
получаем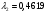 ;
;
Газодинамические функции определяем по формулам:
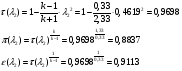
где 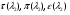 - газодинамические функции температуры, давления и плотности соответственно.
- газодинамические функции температуры, давления и плотности соответственно.
Найдём число Маха:
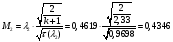
Определение параметров газового потока:
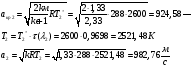
где 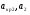 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 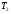 - статическая температура
- статическая температура
Найдем скорость газового потока:
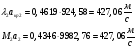
После сечения «k» давление и плотность торможения остаются постоянными:
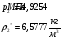
Определим недостающие параметры газового потока:
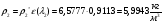
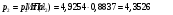
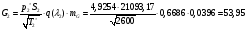
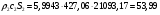
где 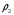 – статическая плотность,
– статическая плотность,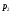 - статическое давление, а
- статическое давление, а 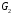 – расход газового потока
– расход газового потока
6)Рассчитаем параметры газового потока для сечения «3»:
Приведенный расход для данного сечения:
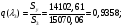
С использованием математического пакета MathCAD определяем величину 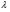 из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении дозвуковой поток, т. е.
из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении дозвуковой поток, т. е. 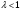 :
:
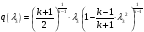 ,
,
получаем 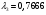 ;
;
Газодинамические функции определяем по формулам:
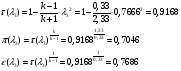
где 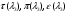 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
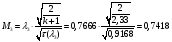
Определение параметров газового потока:
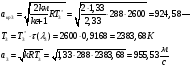
где 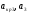 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 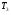 - статическая температура
- статическая температура
Найдем скорость газового потока:
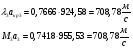
После сечения «k» давление и плотность торможения остаются постоянными:
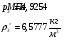
Определим недостающие параметры газового потока:
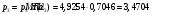
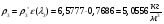
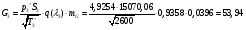
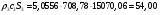
где 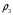 – статическая плотность,
– статическая плотность,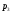 - статическое давление, а
- статическое давление, а 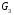 – расход газового потока
– расход газового потока
7)Рассчитаем параметры газового потока для сечения «у»:
Данное сечение критическое, поэтому: q(λу)=1, λу =1, Mу=1.
Газодинамические функции определяем по формулам:
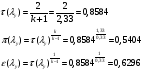
где 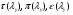 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Определение параметров газового потока:
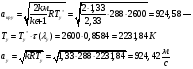
где 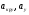 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 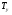 - статическая температура
- статическая температура
Найдем скорость газового потока:
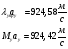
После сечения «k» давление и плотность торможения остаются постоянными:
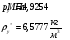
Определим недостающие параметры газового потока:
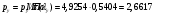

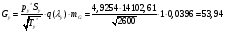
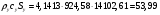
где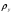 – статическая плотность,
– статическая плотность,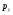 - статическое давление, а
- статическое давление, а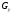 – расход газового потока
– расход газового потока
8)Рассчитаем параметры газового потока для сечения «4»:
Приведенный расход для данного сечения:
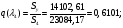
С использованием математического пакета MathCAD определяем величину 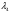 из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении сверхзвуковой поток, т. е.
из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении сверхзвуковой поток, т. е. 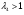 :
:
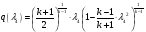 ,
,
получаем 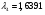 ;
;
Газодинамические функции определяем по формулам:
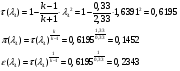
где 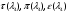 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
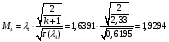
Определение параметров газового потока:
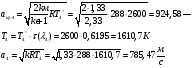
где 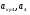 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 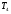 - статическая температура
- статическая температура
Найдем скорость газового потока:
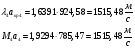
После сечения «k» давление и плотность торможения остаются постоянными:
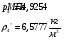
Определим недостающие параметры газового потока:
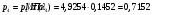
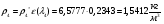
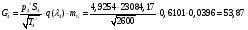
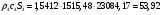
где 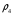 – статическая плотность,
– статическая плотность,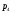 - статическое давление, а
- статическое давление, а 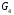 – расход газового потока
– расход газового потока
9)Рассчитаем параметры газового потока для сечения «5»:
Приведенный расход для данного сечения:
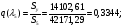
С использованием математического пакета MathCAD определяем величину 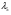 из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении сверхзвуковой поток, т. е.
из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении сверхзвуковой поток, т. е. 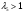 :
:
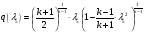 ,
,
получаем 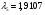 ;
;
Газодинамические функции определяем по формулам:
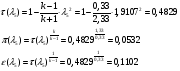
где 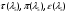 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
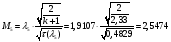
Определение параметров газового потока:
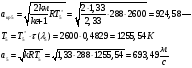
где 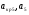 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 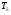 - статическая температура
- статическая температура
Найдем скорость газового потока:
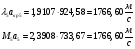
После сечения «k» давление и плотность торможения остаются постоянными:
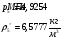
Определим недостающие параметры газового потока:
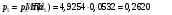
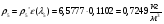
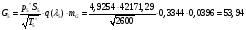
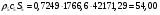
где 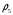 – статическая плотность,
– статическая плотность,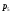 - статическое давление, а
- статическое давление, а 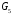 – расход газового потока
– расход газового потока
10)Рассчитаем параметры газового потока для сечения «a»:
Приведенный расход для данного сечения:
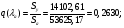
С использованием математического пакета MathCAD определяем величину 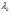 из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении сверхзвуковой поток, т. е.
из решения нелинейного уравнения (см. приложение 3), учитывая, что в данном сечении сверхзвуковой поток, т. е. 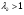 :
:
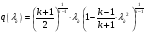 ,
,
получаем 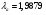 ;
;
Газодинамические функции определяем по формулам:
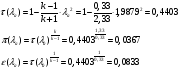
где 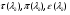 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
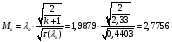
Определение параметров газового потока:
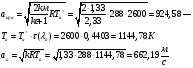
где 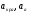 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 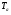 - статическая температура
- статическая температура
Найдем скорость газового потока:
После сечения «k» давление и плотность торможения остаются постоянными:
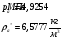
Определим недостающие параметры газового потока:
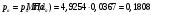
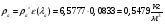
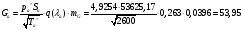
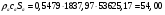
где 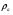 – статическая плотность,
– статическая плотность,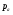 - статическое давление, а
- статическое давление, а 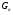 – расход газового потока
– расход газового потока
3. Расчёт второго варианта газового потока.
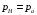 (
(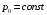 ).
).
Рассчитаем параметры потока со скачком уплотнения в выходном сечении камеры ракетного двигателя.
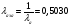 ;
;
Приведенный расход для данного сечения:
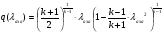
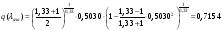
Газодинамические функции определяем по формулам:
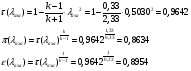
где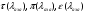 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
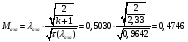
Определение параметров газового потока:
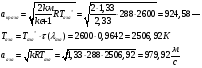
где 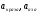 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 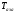 - статическая температура
- статическая температура
Найдем скорость газового потока:
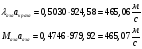
Определим коэффициент изменения давления в прямом скачке уплотнения по формуле:
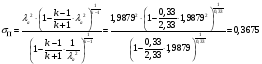
Определим недостающие параметры газового потока:
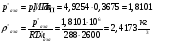
где 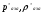 - давление и плотность торможения
- давление и плотность торможения
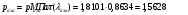
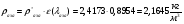
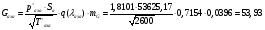
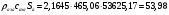
где 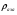 – статическая плотность,
– статическая плотность,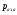 - статическое давление, а
- статическое давление, а 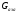 – расход газового потока
– расход газового потока
4. Расчёт третьего варианта газового потока.
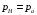 (
(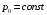 ).
).
Рассчитаем параметры потока со скачком уплотнения в сечении «5» камеры ракетного двигателя.
1) Рассчитаем параметры газового потока для сечения «5за»:
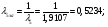
Приведенный расход для данного сечения:
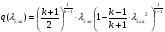
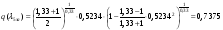
Газодинамические функции определяем по формулам:
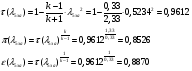
где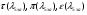 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
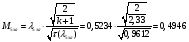
Определение параметров газового потока:
Температура торможения за скачком уплотнения остается постоянной: 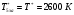
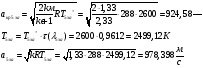
где 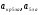 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 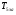 - статическая температура
- статическая температура
Найдем скорость газового потока:
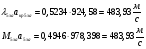
Определим коэффициент изменения давления в прямом скачке уплотнения по формуле:
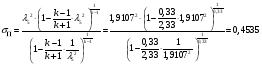
Определим недостающие параметры газового потока:
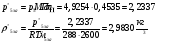
где 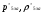 - давление и плотность торможения
- давление и плотность торможения
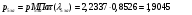
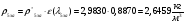
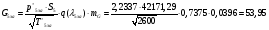
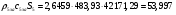
где 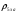 – статическая плотность,
– статическая плотность,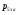 - статическое давление, а
- статическое давление, а 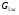 – расход газового потока
– расход газового потока
2) Рассчитаем параметры газового потока для сечения «a»:
Приведенный расход для данного сечения:
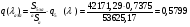 ;
;
С использованием математического пакета MathCAD (см. приложение 3, стр. 68) определяем величину 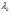 из решения нелинейного уравнения:
из решения нелинейного уравнения:
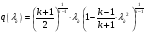 ,
,
получаем 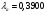
Газодинамические функции определяем по формулам:
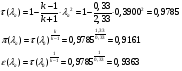
где 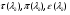 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
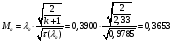
Определение параметров газового потока:
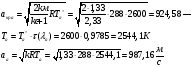
где 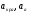 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 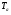 - статическая температура
- статическая температура
Найдем скорость газового потока:
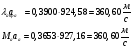
После сечения «k» давление и плотность торможения остаются постоянными:
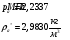
Определим недостающие параметры газового потока:
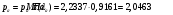
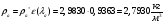
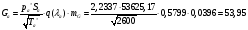
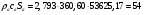
где 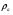 – статическая плотность,
– статическая плотность,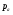 - статическое давление, а
- статическое давление, а 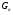 – расход газового потока
– расход газового потока
5. Расчёт четвёртого варианта газового потока.
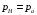 (
(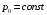 ).
).
Рассчитаем параметры потока со скачком уплотнения в сечении «4» камеры ракетного двигателя.
Рассчитаем параметры газового потока для сечения «4за»:
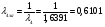
Приведенный расход для данного сечения:
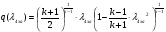
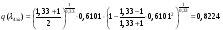
Газодинамические функции определяем по формулам:
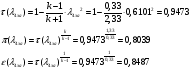
где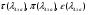 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
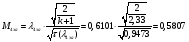
Определение параметров газового потока:
Температура торможения за скачком уплотнения остается постоянной: 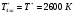
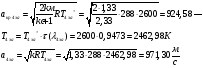
где 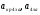 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 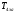 - статическая температура
- статическая температура
Найдем скорость газового потока:
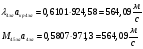
Определим коэффициент изменения давления в прямом скачке уплотнения по формуле:
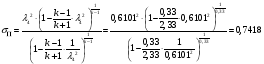
Определим недостающие параметры газового потока:
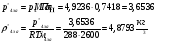
где 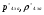 - давление и плотность торможения
- давление и плотность торможения
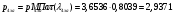
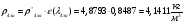
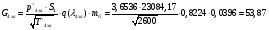
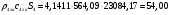
где 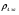 – статическая плотность,
– статическая плотность,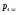 - статическое давление, а
- статическое давление, а 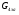 – расход газового потока
– расход газового потока
2) Рассчитаем параметры газового потока для сечения «5»:
Приведенный расход для данного сечения:
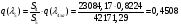 ;
;
С использованием математического пакета MathCAD (см. приложение 3, стр. 70) определяем величину 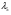 из решения нелинейного уравнения:
из решения нелинейного уравнения:
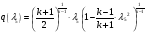 ,
,
получим 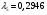 ;
;
Газодинамические функции определяем по формулам:
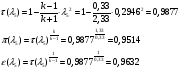
где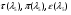 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
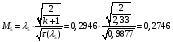
Определение параметров газового потока:
Температура торможения за скачком уплотнения остается постоянной: 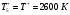
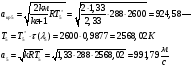
где 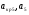 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 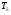 - статическая температура
- статическая температура
Найдем скорость газового потока:
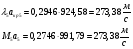
Давление и плотность торможения остаются постоянными:
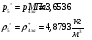
Определим недостающие параметры газового потока:
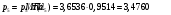
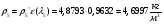
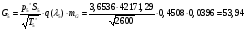
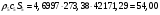
где 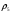 – статическая плотность,
– статическая плотность,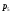 - статическое давление, а
- статическое давление, а 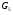 – расход газового потока
– расход газового потока
3) Рассчитаем параметры газового потока для сечения «a»:
Приведенный расход для данного сечения:
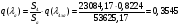 ;
;
С использованием математического пакета MathCAD (см. приложение 3, стр. 71) определяем величину 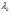 из решения нелинейного уравнения:
из решения нелинейного уравнения:
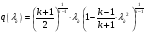 ,
,
получим 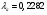 ;
;
Газодинамические функции определяем по формулам:
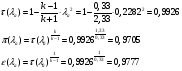
где 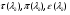 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
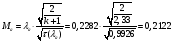
Определение параметров газового потока:
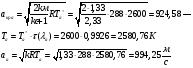
где 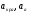 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 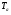 - статическая температура
- статическая температура
Найдем скорость газового потока:
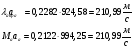
После сечения «k» давление и плотность торможения остаются постоянными:
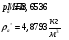
Определим недостающие параметры газового потока:
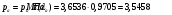
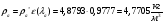
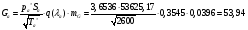
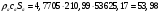
где 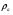 – статическая плотность,
– статическая плотность,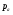 - статическое давление, а
- статическое давление, а 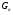 – расход газового потока
– расход газового потока
6. Расчёт пятого варианта газового потока.
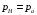 (
(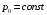 ).
).
Рассчитаем параметры потока со скачком уплотнения в сечении «у» камеры ракетного двигателя.
1) Рассчитаем параметры газового потока для сечения «4»:
Приведенный расход для данного сечения:
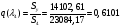 ;
;
С использованием математического пакета MathCAD (см. приложение 3, стр. 72) определяем величину 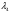 из решения нелинейного уравнения:
из решения нелинейного уравнения:
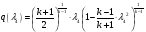 ,
,
получим  ;
;
Газодинамические функции определяем по формулам:
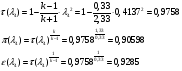
где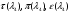 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
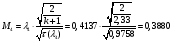
Определение параметров газового потока:
Температура торможения за скачком уплотнения остается постоянной: 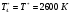
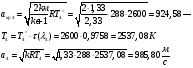
где 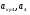 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 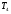 - статическая температура
- статическая температура
Найдем скорость газового потока:
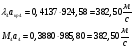
Давление и плотность торможения остаются постоянными:
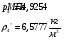
Определим недостающие параметры газового потока:
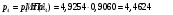
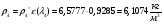
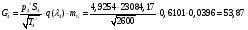
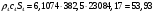
где 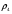 – статическая плотность,
– статическая плотность,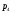 - статическое давление, а
- статическое давление, а 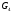 – расход газового потока
– расход газового потока
2) Рассчитаем параметры газового потока для сечения «5»:
Приведенный расход для данного сечения:
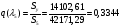 ;
;
С использованием математического пакета MathCAD (см. приложение 3, стр. 70) определяем величину 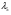 из решения нелинейного уравнения:
из решения нелинейного уравнения:
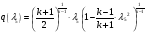 ,
,
получим 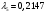 ;
;
Газодинамические функции определяем по формулам:
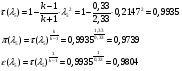
где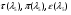 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
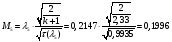
Определение параметров газового потока:
Температура торможения за скачком уплотнения остается постоянной: 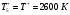
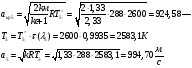
где 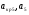 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 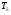 - статическая температура
- статическая температура
Найдем скорость газового потока:
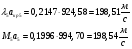
Давление и плотность торможения остаются постоянными:
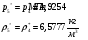
Определим недостающие параметры газового потока:
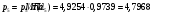
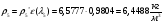
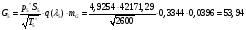
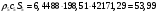
где 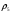 – статическая плотность,
– статическая плотность,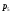 - статическое давление, а
- статическое давление, а 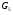 – расход газового потока
– расход газового потока
3) Рассчитаем параметры газового потока для сечения «a»:
Приведенный расход для данного сечения:
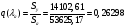 ;
;
С использованием математического пакета MathCAD (см. приложение 3, стр. 71) определяем величину 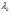 из решения нелинейного уравнения:
из решения нелинейного уравнения:
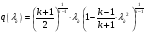 ,
,
получим 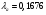 ;
;
Газодинамические функции определяем по формулам:
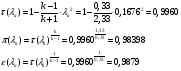
где 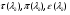 - газодинамические функции температуры, давления и плотности соответственно
- газодинамические функции температуры, давления и плотности соответственно
Найдём число Маха:
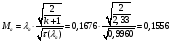
Определение параметров газового потока:
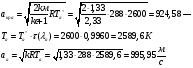
где 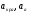 - критическая и местная скорости звука соответственно, а
- критическая и местная скорости звука соответственно, а 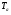 - статическая температура
- статическая температура
Найдем скорость газового потока:
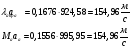
После сечения «k» давление и плотность торможения остаются постоянными:
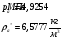
Определим недостающие параметры газового потока:
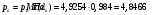
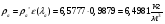
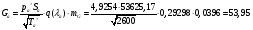
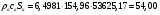
где 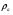 – статическая плотность,
– статическая плотность,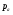 - статическое давление, а
- статическое давление, а 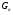 – расход газового потока
– расход газового потока
7. Расчёт импульсов газового потока.
Рассчитаем значения газодинамической функции «f» и количества движения газового потока «Ф» по формулам:
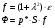 ;
;
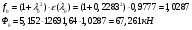
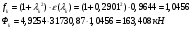
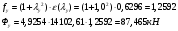
Первый вариант:
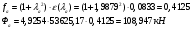
Второй вариант:
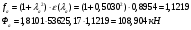
Третий вариант:
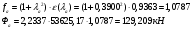
Четвертый вариант:
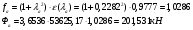
Пятый вариант:
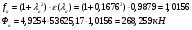
8. Расчёт сил и тяги.
Рассчитаем коэффициенты давления торможения для вариантов работы камеры сгорания 1-5:
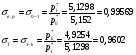
Коэффициенты давления торможения σΠ были получены ранее.
Определяем значения pH из условия, что в любом дозвуковом потоке при истечении во внешнюю среду давление равно pH:
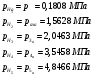
Значения сил P0-k и Pk-y для всех вариантов одинаковы и равны:
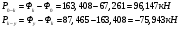
Остальные силы найдем по формулам:

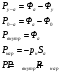
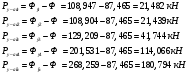
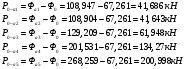
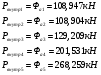
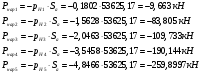
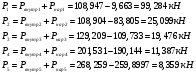
Заключение
В работе рассмотрено поведение газа в канале переменного сечения на сверхзвуковых и дозвуковых режимах, со скачками уплотнения и без них. Вычерчено сечение канала. В результате работы имеем значения основных параметров газового потока, величину расхода по сечениям канала, значения скоростей газовой струи, значения сил взаимодействия потока со стенками сопла. T*1,2=293 К, T*к-аза=2600К; p*0= 5,152, p*1= 5,1298, p*к-аза=4,9254 МПа; ρ*0= 61,05 кг/м3 ρ*1= 60,71 кг/м3, ρ*к-аза= 6,5777 кг/м3; акр0-1= 310,38 м/с, акрк-аза= 924,58м/с; G0 = ρcS0 =53,64кг/с, G1 = ρcS1 =53,96кг/с, Gк-аза = ρcSк-аза =53,94кг/с-в в идеальном случае эти параметры равны из-за округления вычислений эти значения различаются. Рассчитанные в системе MathCAD эти значения равны. Построены графики зависимостей основных характеристик потока от сечения, а также графики зависимостей скорости потока в выходном сечении и сил взаимодействия потока со стенками канала.
Как видно из графиков, на расчетном режиме наблюдается значительное увеличение скорости потока на протяжении всего канала. Вместе с увеличением скорости, уменьшается давление, плотность, температура и скорость звука в газе, параметры торможения остаются постоянными.
Из представленных графиков видно резкое изменение параметров потока на нерасчетных режимах при наличии скачков уплотнений и на дозвуковых режимах: значительное снижение скорости потока, увеличение давления, плотности, температуры и скорости звука в газе, изменяются параметры торможения. Вследствие всего этого уменьшается тяга. Поэтому нерасчетные режимы являются нежелательными и даже недопустимыми для сверхзвукового сопла.
Список используемых источников
1. Расчет идеального газового потока в камере ракетного двигателя /В.А. Курочкин, А.С. Наталевич, А.М. Цыганов, А.А. Диденко// Методические указания: –Самара: СГАУ, 2003. -20с.
2. Абрамович Г.Н. Прикладная газовая динамика, 5-е издание. Часть I. -М.: Наука, 1991. -597с. 4-е издание. –М.: Наука, 1976. -888с.
3. Сергель О.С. Прикладная гидрогазодинамика. –М.: Машиностроение, 1981. -374с.

Нравится материал? Поддержи автора!
Ещё документы из категории промышленность, производство:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ