Элективный курс «Решение задач с параметрами»
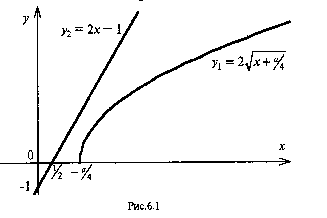
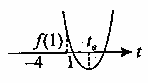
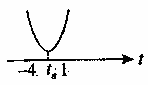
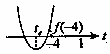
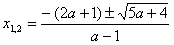
 Муниципальное общеобразовательное учреждение Кадетская школа
Муниципальное общеобразовательное учреждение Кадетская школа
г. Люберцы Московской области
Реферат
Элективный курс
«Решение задач с параметрами»
Учитель математики
Спиридонова Ирина Петровна
-a\4
1
-1
y=2
0
x
y
y=2x-1
Г. Люберцы, 2007 г.
Оглавление
Введение. 3 стр.
Элективный курс «Решение задач с параметрами».
а) Пояснительная записка. 5 стр.
б) Структура курса планирования учебного материала. 7 стр.
в) Краткое содержание курса. 8 стр.
г) Планирование. 12 стр.
д) Методические рекомендации при изучении
некоторых тем. 13 стр.
3. Заключение. 27 стр.
4. Библиографический список. 28 стр.
5. Приложения.
ВВЕДЕНИЕ.
В связи с переходом на профильное обучение возникла необходимость в обеспечении углубленного изучения предмета математики и подготовки учащихся к продолжению образования.
Необходимость перехода старшей школы на профильное обучение определена Правительством России в «Концепции модернизации российского образования на период до 2010 г.», где ставится задача создания специализированной подготовки (профильного обучения) в старших классах общеобразовательной школы, ориентированной на индивидуализацию обучения и социализацию обучающихся, в том числе с учетом реальных потребностей рынка труда, отработки гибкой системы профилей и кооперации старшей ступени школы с учреждениями начального, среднего и высшего профессионального образования».
Принятая в Концепции гибкая система профильного обучения предусматривает возможность разнообразных вариантов комбинаций учебных курсов, осваиваемых старшеклассниками. Эта система включает в себя курсы трех типов: базовые общеобразовательные; профильные общеобразовательные; элективные.
Единый государственный экзамен – это словосочетание знакомо сегодня едва ли не каждой семье, в которой есть школьник. Одной из целей проведения ЕГЭ является совмещение итоговой аттестации выпускников и вступительных испытаний для поступления в ВУЗы. Еще одна из целей введения ЕГЭ – попытка улучшения качества образования в России за счет более высокой мотивации на успешное его прохождение. Теперь детей надо готовить к экзаменам по-иному, так, чтобы они сдавали их успешно, а результаты можно было сравнить. Выдерживать такие экзамены – новая задача, как для школьников, так и для педагогов.
Можно привести один из главных выводов эксперимента с ЕГЭ: «Впервые за сто лет в России появился объективный и абсолютно прозрачный механизм оценки знаний школьников».
На экзаменах прошлых лет в общеобразовательных классах, как правило, задачи с параметрами не решались, а если решались сильными учащимися, то только частично. Решаемость таких заданий не превышала 2% для всех испытуемых.
Каждый ВУЗ предъявляет свои требования к уровню математической подготовки будущего студента, поэтому ВУЗы с большим курсом математики включали в билеты задачи, решить которые, как правило, можно, пройдя специальную целенаправленную подготовку. Вопрос лишь в том, насколько конкурсная задача повышенной сложности обладает диагностической ценностью. Иными словами, можно ли с помощью этой задачи проверить знание основных разделов школьной математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности.
Такой диагностической и прогностической ценностью в полной мере обладают задачи с параметрами.
Практика вступительных экзаменов в ВУЗы по математике показывает, что задачи с параметрами представляют для абитуриентов наибольшую сложность как в логическом, так и в техническом плане и поэтому умение их решать во многом предопределяет успешную сдачу экзамена в любом высшем учебном заведении.
На сегодняшний день задачи с параметрами – неотъемлемая часть ЕГЭ по математике.
Поэтому учителю, прежде всего, необходимо познакомить учеников с приемами решения этих задач, и делать это нужно не от случая к случаю, а регулярно.
Что же такое параметр и почему подобные задачи вызывают такие трудности?
Параметр – это переменная, значение которой считается фиксированным, и каждое значение параметра определяет относительно заданного неизвестного соответствующее уравнение (неравенство, систему).
Иными словами, уравнение с параметром является фактически семейством уравнений, рассматриваемых при фиксированном значении параметра.
Введение параметра способствовало появлению качественно новых типов задач, вдохнуло, если так можно выразиться, новую жизнь в такие традиционные виды задач, как решение уравнений и неравенств. При этом параметры, входящие в условие, существенно влияют на логический и технический ход решения и форму ответа. В этом смысле не всякая задача, в условии которой формально присутствуют параметры («буквы»), является задачей с параметрами.
В процессе подготовки к экзамену необходимо отрабатывать у учащихся умение четко представлять ситуацию, о которой идет речь, анализировать, сопоставлять, устанавливать зависимость между величинами. Важно знакомить учащихся с различными способами решения задачи, а не отдавать предпочтение какому-то одному способу. Ученик должен знать, что при выполнении работы он может выбрать любой способ решения, важно, чтобы задача была решена правильно.
При подготовке к экзамену большое внимание следует уделять накоплению у учащихся опыта самостоятельного поиска решений, чтобы на экзамене каждый ученик был готов к полной самостоятельной работе.
В связи с вышесказанным, возникла необходимость в разработке и внедрении в учебный процесс элективного курса по математике по теме: «Решение задач с параметрами».
Основными формами проведения элективного курса являются изложение узловых вопросов курса в виде обобщающих лекций, семинаров, дискуссий, практикумов по решению задач, рефератов учащихся.
Автор реферата долгое время занималась изучением данной темы в рамках самообразования. В 2001г. ею была разработана «Программа дополнительного образования по математике», в которой задачи с параметрами вводились в курс обучения с 7-го класса. (См. приложения к реферату). Программа была успешно отработана на двух выпусках учащихся. Сейчас это студенты соответственно третьего и второго курсов различных ВУЗов. Все ребята отмечают значимость тех дополнительных знаний, которые они получили на этих занятиях.
Нынешний курс позволяет обобщить и систематизировать весь опыт, накопленный за эти годы; дает возможность за короткое время обучить умению решать достаточно сложные задания.
Разработанный курс направлен на решение следующих задач:
Формирование у учащихся устойчивого интереса к предмету;
Выявление и развитие их математических способностей;
Подготовка к ЕГЭ и к обучению в ВУЗе.
Элективный курс
«Решение задач с параметрами»
Пояснительная записка
Целью профильного обучения, как одного из направлений модернизации математического образования является обеспечение углубленного изучения предмета и подготовка учащихся к продолжению образования.
Основным направлением модернизации математического школьного образования является отработка механизмов итоговой аттестации через введение единого государственного экзамена. В заданиях ЕГЭ по математике с развернутым ответом (часть С) встречаются задачи с параметрами. Обязательны такие задания и на вступительных экзаменах в ВУЗы.
Появление таких заданий на экзаменах далеко не случайно, т.к. с их помощью проверяется техника владения формулами элементарной математики, методами решения уравнений и неравенств, умение выстраивать логическую цепочку рассуждений, уровень логического мышления учащегося и их математической культуры.
Решению задач с параметрами в школьной программе уделяется мало внимания. Большинство учащихся либо вовсе не справляются с такими задачами, либо приводят громоздкие выкладки. Причиной этого является отсутствие системы заданий по данной теме в школьных учебниках.
В связи с этим возникла необходимость в разработке и проведении элективного курса для старшеклассников по теме: «Решение задач с параметрами».
Многообразие задач с параметрами охватывает весь курс школьной математики. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления.
Задачи с параметрами дают прекрасный материал для настоящей учебно-исследовательской работы.
Цель курса
Формировать у учащихся умения и навыки по решению задач с параметрами для подготовки к ЕГЭ и к обучению в ВУЗе.
Изучение курса предполагает формирование у учащихся интереса к предмету, развитие их математических способностей.
Развивать исследовательскую и познавательную деятельность учащихся.
Обеспечить условия для самостоятельной творческой работы.
В результате изучения курса учащийся должен:
усвоить основные приемы и методы решения уравнений, неравенств, систем уравнений с параметрами;
применять алгоритм решения уравнений, неравенств, содержащих параметр;
проводить полное обоснование при решении задач с параметрами;
овладеть исследовательской деятельностью.
Структура курса планирования учебного материала
Темы:
Первоначальные сведения. 2ч
Решения линейных уравнений, содержащих параметры. 2ч
Решения линейных неравенств, содержащих параметры. 2ч
Модуль и параметр. 2ч.
Квадратные уравнения и неравенства, содержащие параметры. 7ч
Свойства квадратичной функции в задачах с параметрами. 4ч
Рациональные уравнения. 2ч
Рациональные неравенства. 2 ч
Иррациональные уравнения. 2ч
Иррациональные неравенства. 2ч
Показательные и логарифмические уравнения, содержащие параметры. 4 ч
Показательные и логарифмические неравенства, содержащие параметры . 4ч
Производная и ее применения. 4ч
Тригонометрия и параметры. 4ч
Графические приемы решения. 4ч
Нестандартные задачи с параметрами. 6ч
количество решений уравнений;
уравнения и неравенства с параметрами с некоторыми условиями.
Текстовые задачи с использованием параметра. 4 ч
Краткое содержание курса
Первоначальные сведения.
Определение параметра. Виды уравнений и неравенств, содержащие параметр.
Основные приемы решения задач с параметрам.
Решение простейших уравнений с параметрами.
Цель: Дать первоначальное представление учащемуся о параметре и помочь привыкнуть к параметру, к необычной форме ответов при решении уравнений.
II. Решение линейных уравнений (и уравнений, приводимых к линейным), содержащих параметр.
Общие подходы к решению линейных уравнений. Решение линейных уравнений, содержащих параметр.
Решение уравнений, приводимых к линейным.
Решение линейно-кусочных уравнений.
Применение алгоритма решения линейных уравнений, содержащих параметр.
Геометрическая интерпретация.
Решение систем уравнений.
Цель: Поиск решения линейных уравнений в общем виде; исследование количества корней в зависимости от значений параметра.
III. Решение линейных неравенств, содержащих параметр.
Определение линейного неравенства.
Алгоритм решения неравенств.
Решение стандартных линейных неравенств, простейших неравенств с параметрами.
Исследование полученного ответа.
Обработка результатов, полученных при решении.
Цель: Выработать навыки решения стандартных неравенств и приводимых к ним, углубленное изучение методов решения линейных неравенств.
IV. Модуль и параметр.
Определение модуля.
Алгоритм решения уравнений и неравенств с модулем.
Раскрытие разных модулей.
Графический способ решения.
Цель: Выработать навыки решения уравнений и неравенств с модулем, содержащих параметр.
V. Квадратные уравнения, содержащие параметр.
Актуализация знаний о квадратном уравнении. Исследования количества корней, в зависимости от дискриминанта. Использование теоремы Виета.
Исследование трехчлена.
Алгоритм решения уравнений.
Графический способ. Аналитический способ решения.
Классификация задач, с позиций применения к ним методов исследования.
Цель: Формировать умение и навыки решения квадратных уравнений с параметрами.
VI. Свойства квадратичной функции в задачах с параметрами.
Область значений функции.
Область определения функции.
Монотонность. Координаты вершины параболы.
Цель: Познакомить с многообразием задач с параметрами, решаемых с помощью свойств квадратичной функции.
VII. Рациональные уравнения.
Общая схема решения целых и дробно-рациональных уравнений.
Решение соответствующих уравнений, содержащих параметр.
Различные способы решения.
Цель: Сформировать умение решать рациональные уравнения с параметром.
Исследование дробно-рациональных уравнений, содержащих параметр.
VIII. Рациональные неравенства.
Общая схема решения, «метод областей».
Различные способы решений.
Цель: Формировать умение и навыки решения рациональных неравенств с параметром.
Иррациональные уравнения.
Схемы решения иррациональных уравнений.
Область определения уравнения.
Решение соответствующих уравнений, содержащих параметр.
Цель: Сформировать умение решать иррациональные уравнения с параметром.
Исследование иррациональных уравнений, содержащих параметр.
Х. Иррациональные неравенства.
Схемы решения иррациональных неравенств.
Решение соответствующих неравенств, содержащих параметр.
Цель: Формировать умение и навыки решения иррациональных неравенств с параметром.
XI. Показательные и логарифмические уравнения, содержащие параметры.
Свойства степеней и показательной функции. Решение показательных уравнений, содержащих параметры.
Свойства логарифмов и логарифмической функции. Решение логарифмических уравнений с параметрами.
Цель: Сформировать умение решать показательные и логарифмические уравнения с параметрами.
XII. Показательные и логарифмические неравенства, содержащие параметры.
Свойства показательной функции. Решение показательных неравенств, содержащих параметры.
Свойства логарифмической функции. Решение логарифмических неравенств с параметрами.
Цель: Формировать умение и навыки решения показательных и логарифмических неравенств с параметром.
XIII. Производная и ее применения.
Касательная к функции.
Критические точки.
Монотонность.
Наибольшие и наименьшие значения функции.
Построение графиков функций.
Цель: Познакомить учащихся с типом задач с параметрами на применение методов дифференциального исчисления.
XIV. Тригонометрия и параметры.
Использование основных свойств тригонометрических функций в задачах с параметрами. Тригонометрические уравнения, содержащие параметр.
Тригонометрические неравенства, содержащие параметр.
Область значений тригонометрических функций.
Цель: Сформировать умение использования свойств тригонометрических функций при решении тригонометрических уравнений и неравенств с параметрами.
XV. Графические приемы решения.
Использование свойств различных функций при решении заданий с параметром.
Специфика решений графическим способом.
Преимущества и недостатки графического способа.
Цель: Научить графическим приемам решения задач с параметром.
XVI. Нестандартные задачи с параметрами.
Использование различных свойств при решении задач с параметрами.
Умение проводить анализ задачи, находить алгоритм решения.
Цель: Формировать навыки исследовательской деятельности, развивать логическое и математическое мышление.
XII. Текстовые задачи с использованием параметра.
Использование различных свойств при решении задач с параметрами.
Умение проводить анализ задачи, находить алгоритм решения.
Цель: Формировать навыки исследовательской деятельности, развивать логическое и математическое мышление.
Планирование (64 часа)
№ урока
Тема
Дата проведения
1
Основные понятия уравнений с параметрами
2
Основные понятия неравенств с параметрами
3 – 4
Решение линейных уравнений с параметрами
5 – 6
Решение линейных неравенств с параметрами
7 – 8
Модуль и параметр
9 – 12
Квадратные уравнения, содержащие параметр
13 – 15
Квадратные неравенства, содержащие параметр
16 – 19
Свойства квадратичной функции
20 – 21
Рациональные уравнения с параметром
22 – 23
Рациональные неравенства с параметрами
24 – 25
Иррациональные уравнения с параметром
26 – 27
Иррациональные неравенства с параметрами
28 – 29
Показательные уравнения с параметром
30 – 31
Логарифмические уравнения с параметром
32 – 33
Показательные неравенства с параметром
34 – 35
Логарифмические неравенства с параметром
36 – 39
Производная и ее применения
40 – 43
Параметры в тригонометрии
44 – 47
Графические приемы решения
48 – 49
Количество решений уравнений
50 – 53
Уравнения и неравенства с параметрами с различными условиями
54 – 57
Текстовые задачи с использованием параметра
58 – 60
Итоговая контрольная работа по курсу
62 – 64
Защита индивидуальных проектов


Методические рекомендации
 при изучении некоторых тем
при изучении некоторых тем
Линейные и квадратные уравнения
Линейное уравнение, записанное в общем виде, можно рассматривать как уравнение с параметрами: ах = b, где х – неизвестное, а, b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.
При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.
Особым значением параметра а является значение а = 0.
1. Если а ≠ 0 , то при любой паре параметров а и b оно имеет единственное решение х = 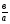 .
.
2. Если а = 0, то уравнение принимает вид: 0 х = b. В этом случае значение b = 0 является особым значением параметра b.
2.1. При b ≠ 0 уравнение решений не имеет.
2.2. При b = 0 уравнение примет вид: 0 х = 0. Решением данного уравнения является любое действительное число.
Пример. Решить уравнение
2а(а — 2) х = а — 2. (1)
Решение. Здесь контрольными будут те значения параметра, при которых коэффициент при х обращается в 0. Такими значениями являются а=0 и а=2. При этих значениях а невозможно деление обеих частей уравнения на коэффициент при х. В то же время при значениях параметра а≠0, а≠2 это деление возможно. Таким образом, целесообразно множество всех действительных значений параметра разбить на подмножества
A1={0}, А2={2} и А3= {а≠0, а≠2}
и решить уравнение (1) на каждом из этих подмножеств, т. е. решить уравнение (1) как семейство уравнений, получающихся из него при следующих значениях параметра:
1) а=0 ; 2) а=2 ; 3) а≠0, а≠2.
Рассмотрим эти случаи.
1) При а=0 уравнение (1) принимает вид 0 х = - 2. Это уравнение не имеет корней.
2) При а=2 уравнение (1) принимает вид 0 х=0. Корнем этого уравнения является любое действительное число.
3) При а≠0, а≠2 из уравнения (1) получаем, х = 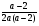 ,
,
откуда х = 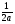 .
.
0твет: 1) Если а=0,то корней нет;
2)если а=2, то х – любое действительное число;
3) если а≠0, а≠2 , то х =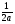 .
.
Пример. Решить уравнение
(а — 1) х2+2 (2а+1) х+(4а+3) =0; (2)
Решение. В данном случае контрольным является значение a=1. Дело в том, что при a=1 уравнение (2) является линейным, а при а≠ 1 оно квадратное (в этом и состоит качественное изменение уравнения). Значит, целесообразно рассмотреть уравнение (2) как семейство уравнений, получающихся из него при следующих значениях параметра: 1) а = l; 2) а≠1.
Рассмотрим эти случаи.
1) При a=1 уравнение (2) примет вид 6х+7=0. Из этого
уравнения находим х = -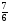 .
.
2) Из множества значений параметра а ≠ 1 выделим те значения, при которых дискриминант уравнения (2) обращается в 0.
Дело в том, что если дискриминант D=0 при а=ао, то при переходе значения D через точку ао дискриминант может изменить знак (например, при а<ао D< 0, а при а>ао D>0). Вместе с этим при переходе через точку ао меняется и число действительных корней квадратного уравнения (в нашем примере при а<ао корней нет, так как D< 0, а при а>ао D>0 уравнение имеет два корня). Значит, можно говорить о качественном изменении уравнения. Поэтому значения параметра, при которых обращается в 0 дискриминант квадратного уравнения, также относят к контрольным значениям.
Составим дискриминант уравнения (2):
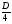 =(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем
=(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем 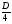 = 5а+4.
= 5а+4.
Из уравнения 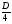 = 0 находим а = -
= 0 находим а = -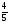 — второе контрольное значение параметра а. При
— второе контрольное значение параметра а. При
этом если а <-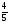 , то D <0; если a≥-
, то D <0; если a≥-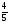 , то D≥0, a ≠ 1.
, то D≥0, a ≠ 1.
Таким образом, осталось решить уравнение (2) в случае, когда а <-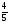 и в случае, когда { a≥-
и в случае, когда { a≥-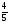 , a ≠ 1 }.
, a ≠ 1 }.
Если а <-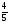 , то уравнение (2) не имеет действительных корней; если же
, то уравнение (2) не имеет действительных корней; если же
{ a≥-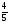 , a ≠ 1 }, то находим
, a ≠ 1 }, то находим
Ответ: 1) если а <-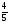 , то корней нет;
, то корней нет;
2) если а = 1, то х = -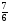 ;
;
3) если a≥-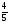 , a ≠ 1, то .
, a ≠ 1, то .
Свойства квадратичной функции
в задачах с параметрами
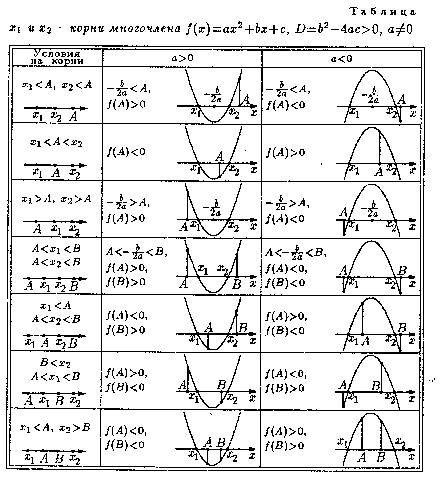
При решении различных задач часто используются не только свойства квадратного уравнения, но и свойства квадратичной функции. Полезно дать учащимся таблицу, позволяющую составлять систему неравенств для нахождения решений задачи. Однако, на мой взгляд, для рационального подхода к поиску решения достаточно рассмотреть только расположение графиков при положительном старшем коэффициенте, но обратить внимание, что тогда неравенства составляются в виде  аf(A)< 0 или аf(A)> 0 (а- старший коэффициент).
аf(A)< 0 или аf(A)> 0 (а- старший коэффициент).
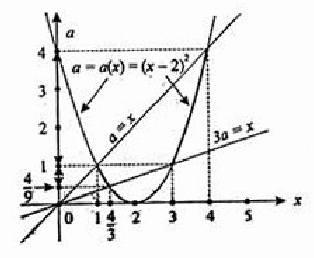
Пример. При каких значениях параметра а один из корней уравнения
(а2-2)х2+(а2+а-1)х-а3+а=0
больше числа а, а другой меньше числа а?
Решение. Задача равносильна следующей: при каких значениях параметра а нули квадратичной функции
g(х)= (а2-2)х2+(а2+а-1)х-а3+а
лежат на вещественной оси по разные стороны от точки х = а?
Исходя из таблицы, имеем условие: аf(A)< 0.
В нашем случае это условие принимает вид
(а2-2) g(а)<0.
Следовательно, требованию задачи удовлетворяют решения неравенства
(а2-2)((а2-2)а2+(а2+а-1)а-а3+а)<0, где а2-2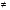 0 (а =
0 (а = , а =-
, а =- требованию задачи не удовлетворяют).
требованию задачи не удовлетворяют).
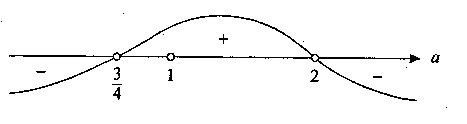
Решая полученное неравенство,
находим, что а (-
(- ; -1)
; -1) (1;
(1;  ).
).
Ответ: При а (-
(- ; -1)
; -1) (1;
(1;  ).
).
Пример. При каких значениях параметра 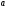 корни уравнения
корни уравнения
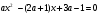 (1)
(1)
больше 1?
Решение. Очевидно, что задача равносильна следующей: при каких значениях параметра 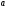 корни квадратного трехчлена
корни квадратного трехчлена
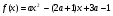
больше 1?
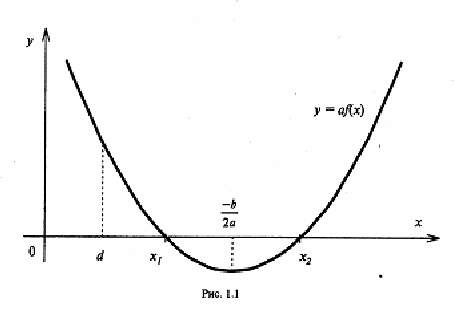
Переход от одной формулировки задачи к другой подчеркивает ту общую часто используемую при решении алгебраических уравнений второй степени идею, которая связана с описанием тех или иных свойств квадратного трехчлена и их геометрической интерпретации на графике. В частности, для того, чтобы корни квадратного трехчлена
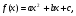
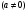 (2)
(2)
были больше числа 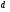 , необходимо и достаточно выполнение условий
, необходимо и достаточно выполнение условий
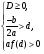 (3)
(3)
(см. рис. 1.1.)
Условия (3) равносильны условиям
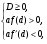
где 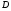 - дискриминант, а
- дискриминант, а 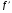 - производная квадратного трехчлена. Требование же того, чтобы корни квадратного трехчлена были меньше числа
- производная квадратного трехчлена. Требование же того, чтобы корни квадратного трехчлена были меньше числа 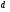 , означает выполнение условий
, означает выполнение условий
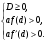
Возвращаясь к исходной задаче, замечаем, что при 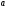 =0 уравнение (1) имеет корень
=0 уравнение (1) имеет корень  , который требованиям задачи не удовлетворяет.
, который требованиям задачи не удовлетворяет.
Рассмотрим случай 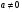 . При таких
. При таких 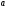 условия (3) запишутся в виде
условия (3) запишутся в виде
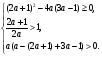
Решая эту систему, находим, что 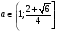 .
.
Очевидно, что этот же результат мы получили бы и решая неравенство 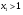 , где
, где 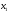 - меньший корень уравнения (1)
- меньший корень уравнения (1)
Ответ: 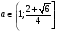 .
.
Рациональные неравенства с параметрами
Пример. Найти все значения параметра 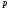 , при которых неравенство
, при которых неравенство
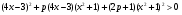
выполняется при всех 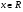 .
.
Решение. Исходное неравенство является однородным неравенством второй степени относительно функции 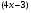 и
и 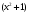 . Если разделить его на
. Если разделить его на  , то получится равносильное неравенство
, то получится равносильное неравенство
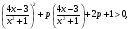
которое после замены 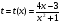 становится квадратным неравенством относительно переменной
становится квадратным неравенством относительно переменной 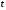 с параметром
с параметром 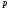 :
:
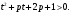 (*)
(*)
Найдем множество значений функции 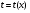 при
при 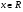 . Имеем:
. Имеем: 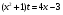 , то есть
, то есть 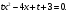 Отсюда
Отсюда 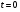 при
при 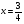 ; другие значения
; другие значения 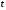 (отличные от нуля) найдем из условия неотрицательности дискриминанта этого квадратного уравнения:
(отличные от нуля) найдем из условия неотрицательности дискриминанта этого квадратного уравнения: 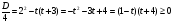 , то есть
, то есть 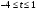 .
.
Итак, исходное неравенство выполняется для всех 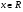 тогда и только тогда, когда неравенство (*) выполняется для всех
тогда и только тогда, когда неравенство (*) выполняется для всех 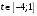 .
.
Рассмотрим квадратный трехчлен 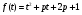 с абсциссой вершины
с абсциссой вершины 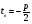 и дискриминантом
и дискриминантом 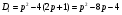 . Тогда имеем следующие необходимые и достаточные условия для нахождения искомых значений параметра
. Тогда имеем следующие необходимые и достаточные условия для нахождения искомых значений параметра 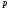 :
:
(1) (2) (3)
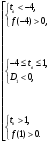
Последовательно преобразуя, получаем:
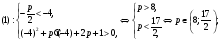
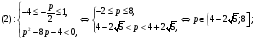
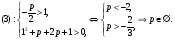
Объединяя решения систем (1)-(3), получаем ответ.
Ответ: 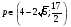
Иррациональные уравнения с параметрами
Существует несколько способов решения иррациональных уравнений с параметрами. Познакомимся с ними, разобрав следующий пример.
Пример. В зависимости от значений параметра 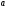 решить уравнение
решить уравнение
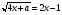 (1)
(1)
Решение. Решим уравнение (1) пятью способами, которые необходимо знать, ибо наряду с другими подходами они могут быть использованы и при решении иных типов уравнений.
Способ 1. Уравнение (1) равносильно системе
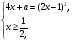
или системе
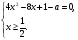 (2)
(2)
Решая уравнение из системы (2), находим
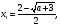
 (3)
(3)
откуда следует, что при 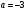 уравнение (1) имеет одно решение
уравнение (1) имеет одно решение 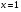 . Если
. Если 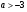 , то
, то 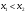 , и тогда уравнение (1) будет иметь два решения при тех значениях параметра
, и тогда уравнение (1) будет иметь два решения при тех значениях параметра 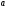 , при которых совместна система
, при которых совместна система
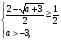 ,
,
т.е. при 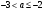
Уравнение (1) будет иметь только один корень 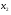 , если
, если 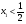 , а
, а 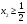 . В этом случае решая систему
. В этом случае решая систему
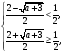
приходим к выводу, что 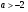 .
.
Замечая теперь, что при 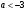 дискриминант уравнения системы (2) отрицателен, получаем
дискриминант уравнения системы (2) отрицателен, получаем
Ответ: если 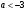 , то решений нет;
, то решений нет;
если 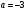 , то
, то 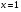 ;
;
если 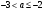 , то
, то 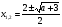 ;
;
если 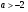 , то
, то 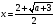 .
.
Способ 2. Возведя обе части уравнения (1) в квадрат, получим уравнение из системы (2), корни которого задаются формулами (3). Но здесь надо иметь в виду, что при возведении обеих частей уравнения (1) в квадрат могли появиться посторонние корни.
Поэтому при данном способе решения необходимо произвести проверку. Так, подставляя корень 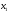 в исходное уравнение, придем к соотношению
в исходное уравнение, придем к соотношению
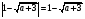 ,
,
откуда 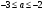 .
.
Если же подставить корень 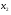 в уравнение (1), то придем уже к отношению
в уравнение (1), то придем уже к отношению 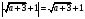 , и, таким образом,
, и, таким образом, 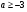 .
.
Учитывая теперь, что при 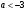 корней нет, а при
корней нет, а при 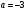 имеем
имеем 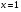 , получаем тот же ответ, что и при первом способе решения.
, получаем тот же ответ, что и при первом способе решения.
Способ 3. Если воспользоваться геометрическим смыслом квадратного трехчлена, то, обращаясь к равносильной уравнению (1) в системе (2), приходим к выводу, что уравнение (1)будет иметь корни 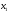 и
и 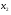 в том случае, когда корни квадратного трехчлена
в том случае, когда корни квадратного трехчлена 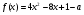 не меньше
не меньше 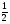 . Аналитически соответствующие условия записываются в виде системы
. Аналитически соответствующие условия записываются в виде системы
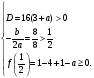
Решая эту систему, находим, что 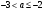 .
.
При 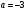 уравнение (1) имеет решение
уравнение (1) имеет решение 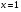 .
.
Если же 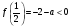 , т.е.
, т.е. 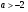 , то уравнение (1) будет иметь один корень
, то уравнение (1) будет иметь один корень 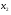 . При
. При 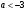 решений нет.
решений нет.
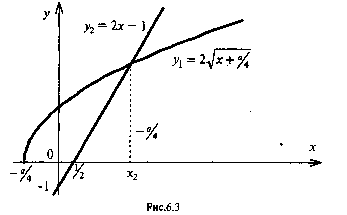
Способ 4. Рассмотрим графики функций
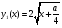 и
и 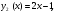
заданных соответственно левой и правой частями уравнения (6.1).
Абсциссы точек пересечения этих графиков и будут решениями уравнения (1). При 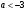 графики не пересекаются (см. рис. 6.1) и значит уравнение (1) решений не имеет.
графики не пересекаются (см. рис. 6.1) и значит уравнение (1) решений не имеет.
При 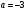 графики касаются и уравнение (1) имеет один корень
графики касаются и уравнение (1) имеет один корень 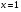 .
.
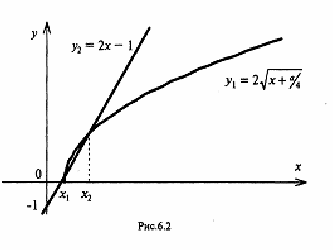
При 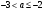 уравнение (1) будет иметь корни
уравнение (1) будет иметь корни 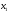 и
и 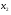 , определяемые формулами (3) (см. рис. 6.2).
, определяемые формулами (3) (см. рис. 6.2).
При 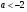 графики функций
графики функций 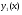 и
и 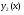 пересекаются в одной точке, и значит уравнение (1) имеет одно решение
пересекаются в одной точке, и значит уравнение (1) имеет одно решение 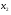 (см. рис. 6.3)
(см. рис. 6.3)
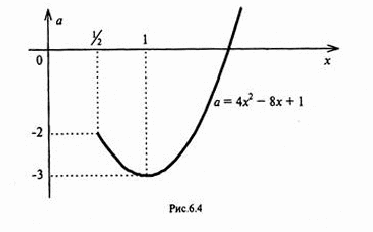
Способ 5. Перепишем равносильную уравнению (1) систему (2) в виде
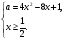
Построив тогда в плоскости 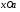 график функции
график функции 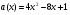 при условии
при условии 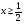 (см. рис. 6.4), мы приходим к выводам, полученным ранее четырьмя рассмотренными способами.
(см. рис. 6.4), мы приходим к выводам, полученным ранее четырьмя рассмотренными способами.
Ответ: если 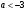 , то решений нет;
, то решений нет;
если 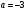 , то
, то 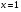 ;
;
если 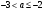 , то
, то 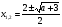 ;
;
если 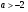 , то
, то 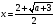 .
.
Показательные и логарифмические неравенства с параметрами
Пример. Найти все значения параметра 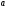 , при которых неравенство
, при которых неравенство
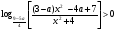
выполняется для всех действительных значений 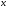 .
.
Решение. Исходное неравенство
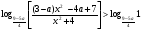
равносильно следующей совокупности двух систем:
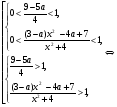
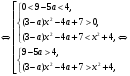
(1) (2) (1) (2)
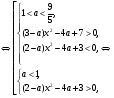
В системе (1) параметр 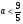 , поэтому коэффициент
, поэтому коэффициент 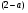 , стоящий при
, стоящий при 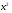 в левой части последнего неравенства, положителен, следовательно, последнее неравенство системы (1) равносильно неравенству
в левой части последнего неравенства, положителен, следовательно, последнее неравенство системы (1) равносильно неравенству

которое не может выполняться при всех действительных значениях 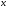 при любом фиксированном значении параметра
при любом фиксированном значении параметра 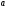 . Таким образом, система (1) не дает искомых значений параметра.
. Таким образом, система (1) не дает искомых значений параметра.
В системе
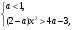 (2)
(2)
из первого неравенства (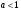 ) так же, как и раньше, вытекает, что
) так же, как и раньше, вытекает, что 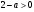 , следовательно, второе неравенство равносильно неравенству
, следовательно, второе неравенство равносильно неравенству
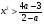 ,
,
которое, очевидно, выполняется для всех действительных 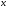 тогда и только тогда, когда
тогда и только тогда, когда
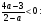
С учетом того, что 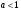 , получаем
, получаем 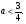
Ответ: 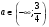
Производная и ее применения
Пример. Найти все значения параметра 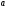 , при которых функция
, при которых функция
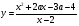
имеет хотя бы один экстремум строго между числами 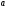 и
и 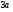 .
.
Решение. Для вычисления экстремумов функции  найдем её производную:
найдем её производную:
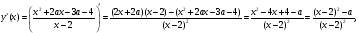 откуда следует, что в точках экстремума, то есть при
откуда следует, что в точках экстремума, то есть при 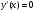 , значение параметра
, значение параметра 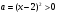 , так как
, так как 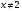 . Поэтому интервал
. Поэтому интервал 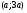 , на котором, согласно условию задачи, надо искать экстремум, целиком расположен справа от точки 0.
, на котором, согласно условию задачи, надо искать экстремум, целиком расположен справа от точки 0.
Дальнейшее решение задачи изложим двумя способами.
I- ый способ. Рассмотрим квадратный трехчлен 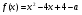 с абсциссой вершины
с абсциссой вершины 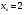 и дискриминантом
и дискриминантом 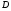 , положительность которого следует из того, что
, положительность которого следует из того, что 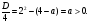
Если абсцисса 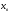 вершины параболы, являющейся графиком функции
вершины параболы, являющейся графиком функции 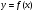 , расположена левее интервала
, расположена левее интервала 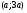 , то есть величина
, то есть величина 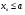 , то значения
, то значения 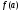 и
и 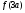 должны быть разных знаков, причем
должны быть разных знаков, причем 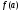 - отрицательно:
- отрицательно:
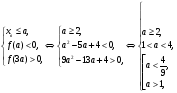
откуда следует, что 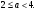
Если 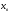 лежит строго между
лежит строго между 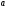 и
и 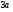 , то либо
, то либо 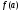 , либо
, либо 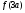 должно быть положительно:
должно быть положительно:
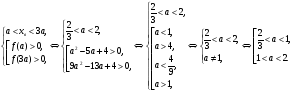
Если 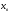 лежит правее интервала
лежит правее интервала 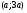 , то есть
, то есть 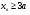 , то значения
, то значения 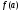 и
и 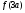 должны быть разных знаков, причем
должны быть разных знаков, причем 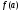 - положительно:
- положительно:
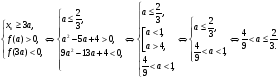
Объединяя найденные значения параметра 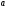 в рассмотренных трех случаях
в рассмотренных трех случаях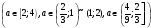 , получает ответ:
, получает ответ: 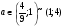 .
.
II – й способ.
Как мы уже получили ранее, в точках экстремума, то есть при 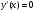 имеем
имеем 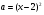 . В плоскости
. В плоскости 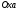 нарисуем график функции
нарисуем график функции 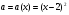 . Точки экстремума будем искать на интервале
. Точки экстремума будем искать на интервале 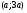 , то есть при
, то есть при 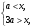 что соответствует внутренним точкам острого угла, ограниченного прямыми
что соответствует внутренним точкам острого угла, ограниченного прямыми 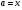 и
и  , и находящегося в первой четверти. Найдем точки пересечения прямых
, и находящегося в первой четверти. Найдем точки пересечения прямых 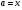 и
и  с параболой
с параболой 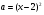 . Решая квадратные уравнения, получаем:
. Решая квадратные уравнения, получаем:
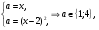
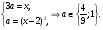
Так как производная 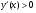 при
при 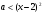 и
и 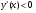 при
при 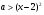 , то исходная функция
, то исходная функция  является возрастающей в области
является возрастающей в области  , расположенной ниже параболы
, расположенной ниже параболы 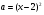 , и убывающей в области, расположенной выше этой параболы; в точках параболы функция
, и убывающей в области, расположенной выше этой параболы; в точках параболы функция  имеет экстремум (в силу того, что выполнено достаточное условие экстремума – смена знака производной).
имеет экстремум (в силу того, что выполнено достаточное условие экстремума – смена знака производной).
Левая ветвь параболы 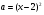 пересекается с прямыми
пересекается с прямыми  и
и 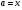 в точках
в точках 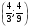 и
и 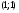 соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции
соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции  , соответствующим искомым значениям параметра
, соответствующим искомым значениям параметра 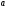 :
: 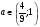 (проекция на ось
(проекция на ось 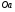 указанного участка левой ветви параболы
указанного участка левой ветви параболы 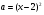 ).
).
Правая ветвь параболы 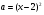 пересекается с прямыми
пересекается с прямыми  и
и 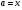 в точках
в точках 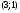 и
и 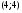 соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции
соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции  , соответствующим искомым значениям параметра
, соответствующим искомым значениям параметра 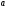 :
: 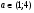 (проекция на ось
(проекция на ось 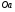 указанного участка правой ветви параболы
указанного участка правой ветви параболы 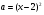 ).
).
Объединяя найденные выше интервалы 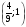 и
и 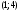 значений параметра
значений параметра 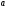 , получаем ответ.
, получаем ответ.
Ответ: 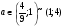 .
.
Заключение
Введение элективного курса «Решение задач с параметрами» необходимо учащимся в наше время как при подготовке к ЕГЭ, так и к вступительным экзаменам в ВУЗы. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики.
Даже если бы эти задачи не предлагались на выпускных и вступительных экзаменах, то все равно в школьной математике задачам с параметрами должно уделяться большое внимание. В этом автор данного реферата глубоко убеждена: ведь известно, какую роль играют данные задачи в формировании логического мышления и математической культуры у школьников. Поэтому учащиеся, владеющие методами решения задач с параметрами, успешно справляются (и опыт это подтверждает) с другими задачами. Решение задач, уравнений с параметрами открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях и на любом другом математическом материале.
При решении задач с параметрами одновременно активно реализуются основные методические принципы:
принцип параллельности – следует постоянно держать в поле зрения несколько тем, постепенно продвигаясь по ним вперед и вглубь;
принцип вариативности – рассматриваются различные приемы и методы решения с различных точек зрения: стандартность и оригинальность, объем вычислительной и исследовательской работы;
принцип самоконтроля – невозможность подстроиться под ответ вынуждает делать регулярный и систематический анализ своих ошибок и неудач;
принцип регулярности – увлеченные математикой дети с удовольствием дома индивидуально исследуют задачи, т. е. занятия математикой становятся регулярными, а не от случая к случаю на уроках.
Разработанный элективный курс может быть использован учителями математики при подготовке к ЕГЭ, вступительным экзаменам в ВУЗы, на занятиях математического кружка. В нем систематизирован теоретический и дидактический материал, отвечающий принципу последовательного нарастания сложности.
Библиографический список.
Амелькин. В. В., Рабцевич В. Л. Задачи с параметрами. Справочное пособие по математике. – 2-е изд. - Мн. ООО «Асар», 2002. – 464 с.; ил.
Галицкий М. Л. и др. Сборник задач по алгебре для учащихся шк. и кл. с углубл. изуч. математики. – 4-е изд. – Просвещение, 1997. – 271 с.; ил.
Горнштейн П. И., Полонский В. Б., Якир М. С. Задачи с параметрами. – 3-е изд. – М.; Илекса, Харьков: Гимназия, 1998, - 336 с.
Дорофеев Г. В. и др. Математика: Для поступающих в вузы: Пособие. – 5-е изд. – М.: Дрофа, 2002. – 672 с.; ил.
Сканави М. И. и др. Сборник задач по математике для поступающих во втузы. – 7-е изд. – М. 1996. – 528 с.; ил.
Мордкович и др. Алгебра и начала анализа. 10-11 кл.: Задачник для общеобразоват. учреждений. – М.: Мнемозина, 2000. – 315 с; ил.
Макарычев Ю. Н., Миндюк Н. Г. Алгебра: Доп. главы к шк. и кл. с углубл. изуч. матаматики. – М.: Просвещение,1997. – 224 с.; ил.
Саакян С. М. и др. задачи по алгебре и началам анализа: Пособие для учащихся 10-11 кл. общеобразоват.учреждений. – М.: Просвещение, 1997. – 256 с.; ил.
Черкасов О. Ю.Якушев А. Г. Математика для поступающих в серьезные вузы. – М.: Московский лицей, 1998. – 400 с.
Говоров В. М. и др. Математика: сборник задач с решениями для поступающих в вузы. – М.: АСТ: Астрель,2005. – 829 с.; ил.
Шарыгин И. Ф. Сборник задач по математике с решениями: Учеб. пособие для 11 кл. общеобразоват. учреждений. – М.: АСТ: Астрель, 2001. – 448 с.; ил.
Ромашко В. Д. Параметры. – Интернет.
Карп. А. П. Сборник задач для подготовки к выпускным экзаменам по алгебре и началам анализа. – Санкт-Петербург: Оракул, 1998. – 284 с.
Бортаковский А. С., Закалюкин В. М. Задачи повышенной сложности по математике для абитуриентов, - М.: Изд-во МАИ, 2003. – 424 с.
Бортаковский А. С., Закалюкин В., Шапошников В. П. Экзаменационные задачи и варианты по математике: Учебное пособие. – 3-е изд. – М.: Изд-во МАИ, 2004. – 384 с.
Олехник С. Н., Потапов М. К., Пасиченко П. И. Алгебра и начала анализа. Уравнения и неравенства. Учебно-методическое пособие для учащихся 10-11 кл. – М.: Экзамен, 1998. – 192 с.
Горнштейн П. И., Мерзляк А. Г., Полонский В. Б. Якир М. С. Экзамен по математике и его подводные рифы. – М.: Илекса, Харьков:Гимназия, 1998. – 236 с.
Сергеев И. Н. Математика. Задачи с ответами и решениями: Пособие для поступающих в вузы. – М.:КДУ, 2005. – 3-е изд. – 360 с.; ил.
Приходько Л. А., Грознова С. Ю. Математика: Пособие для поступающих в 10-ый лицейский класс. – М.: Изд-во Рос. экон. акад., 2002. – 69 с.
Лебедев В. В. Решения задач репетиционного экзамена по математике 2002-2004 г. М.: «Экспресс-Полиграф-Сервис»., - 2002.
Потапов М. К.., Олехник С. Н.,Нестеренко Ю. В. Уравнения и неравенства с параметрами. – Изд-во Московского университета, 1992. – 16 с.
Осколков В. А. и др. Сборник конкурсных задач по математике с решениями и ответами. – М.: МИФИ, 2003. – 92 с.
Сборники «Математика. ЕГЭ». – М.: Экзамен,2004, 2005, 2006.
Сборники «Математика. ЕГЭ». – М.: АСТ: Астрель,2006, 2007.
Сборники «Математика. ЕГЭ». – М.: Просвещение, 2005-2007.
Мерзляк А. Г., Полонский В. Б., Рабинович Е. М., Якир М. С. Сборник задач и контрольных работ (7-9 кл.). – Москва-Харьков: Илекса, Гимназия, 1999.
Ершова А. П., Голобородько В. В., Ершова А. С. Самостоятельные и контрольные работы по алгебре (7-11 кл)

Нравится материал? Поддержи автора!
Ещё документы из категории разное:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ