Методические рекомендации Иркутск 2010 удк 371 ббк 371 29

Министерство образования ИРКУТСКОЙ ОБЛАСТИ

ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ автономное ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ДОПОЛНИТЕЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

(повышения квалификации) специалистов

«институт развития образования ИРКУТСКОЙ ОБЛАСТИ»

результатЫ
государственноЙ (ИТОГОВОЙ) АТТЕСТАЦИИ ВЫПУСКНИКОВ 9-Х КЛАССОВ
В НОВОЙ ФОРМЕ

Математика

выпуск 13

Методические рекомендации

Иркутск

2010

УДК 371

ББК 371 29

Р 34

Результаты государственной (итоговой) аттестации выпускников 9-х классов в новой форме.

Математика: Методические рекомендации. Выпуск 13

Авторы:. Марков С.Н., к.ф-м.н., Бокмельдер Е.П.,к.ф-м.н., Осипенко Л.А., к.ф-м.н.

ISBN 978-5-85827-380-6

Статистические данные представлены РЦОИ – программный комплекс ТОЭ ФИПИ, центром автоматизации управления – программа «1С:Хронограф
Школа 2.5»

Методические рекомендации предназначены для работников системы образования: учителей, руководителей общеобразовательных учреждений, специалистов органов управления образованием, преподавателей и руководителей учреждений начального и среднего профессионального образования, могут быть интересны обучающимся, их родителям, представителям широкой общественности.

УДК 371

ББК 371 29

Рецензенты: Басюк В.С., к.псх.н. – министр образования Иркутской области

Гетманская И. А., к.п.н. – заместитель директора по НМ и ИД ОГАОУ ДПО ИРО

Редколлегия: Каменяр И.Н., Крашенинникова Л.А., Чибирякова Т.В.

Верстка: Воробьев В.В., Ревенко О.С.

ISBN 978-5-85827-380-6

Содержание

I.ОБЩИЕ РЕЗУЛЬТАТЫ ГОСУДАРСТВЕННОЙ ИТОГОВОЙ АТТЕСТАЦИИ (ДАЛЕЕ - ГИА) В НОВОЙ ФОРМЕ ВЫПУСКНИКОВ

9-Х КЛАССОВ ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЙ ИРКУТСКОЙ ОБЛАСТИ ПО МАТЕМАТИКЕ

1.1. Характеристика и количество участников

Для участия в экзамене было зарегистрировано 27827 учащихся 9-х классов общеобразовательных учебных заведений, лицеев и гимназий. Всего приняли участие в экзамене 26572 человека (в 2009г. принимали участие 22341 человека), что составляет 95,5% от общего числа зарегистрированных.

1.2. Рейтинг по количеству участников

Рейтинговый ряд образовательных учреждений

Таблица 1

Вид образовательного учреждения

Количество участников

Процент участников

Лицеи и лицей-интернат

1563

5,9

Гимназия

1261

4,7

Общеобразовательная школа-интернат среднего (полного) общего образования, в т.ч. с углубленным изучения отдельных предметов

279

1,1

Средняя общеобразовательная школа с углубленным изучением предмета

593

2,2

Средняя общеобразовательная школа

21417

80,6

Открытые (сменные) общеобразовательные школы

219

0,8

Вечерние (сменные) общеобразовательные школы

153

0,6

Основные общеобразовательные школы

677

2,5

Центры образования

348

1,3

Кадетская школа-интернат

0,3

Всего участников

26572

100%

Всего 82 ученика (0,3%) получили высший балл (то есть 32 балла).

Отметим ещё, что полностью нулевых работ оказалось 126 (0,5%).

1.3. Анализ данных по гендерному признаку

Таблица 2

Количество

девушек

Средний балл

девушек

Количество

юношей

Средний балл

юношей

13265 (49,9%)

3,17

13307 (50,1%)

3,01

Таким образом, девушки сдали экзамен в среднем лучше, чем юноши.

1.4. Средняя отметка

Средняя отметка по области составила 3,1. При этом средняя отметка колебалась по городским школам от 2,8 до 3,5, а по по сельским школам – от 2,5 до 3,2 .

1.5. Средний первичный балл

Средний первичный балл по области составил 11,8 (при максимально возможных 32 баллах). При этом средний балл колебался по городским школам от 9,5 до 14,7, а по по сельским школам – от 7,3 до 13,4.

1.6. Рейтинговый ряд общеобразовательных учреждений по среднему баллу

Таблица 3

Вид образовательного учреждения

Количество участников

Процент участников

Средняя отметка 2010 г.

Средняя отметка 2009 г.

Лицеи и лицей-интернат

1563

5,9

4,1

Гимназия

1261

4,7

3,7

3.6

Средняя общеобразовательная школа с углубленным изучением предмета

593

2,2

3,3

3,1

279

1,1

3,2

3.7

Основные общеобразовательные школы

677

2,5

Средняя общеобразовательная школа

21417

80,6

2,8

Кадетская школа-интернат

0,3

2,9

Открытые (сменные) общеобразовательные школы

219

0,8

2,7

2,5

Вечерние (сменные) общеобразовательные школы

153

0,6

2,7

2,4

Центры образования

348

1,3

2,7

2,1

Всего участников

26572

100%

средний балл 3,1

средний балл 2,8

Из приведённых данных видно, что средний балл лицеев и гимназий значительно (на 0,7-1,1 балла) выше, чем средний балл общеобразовательных школ. Для лицеев такой результат закономерен, т.к. лицеи имеют естественнонаучный профиль и возможность отбора детей при поступлении в лицеи. Гимназии имеют гуманитарный профиль и их сравнительно высокий результат можно объяснить возможностью отбора детей при поступлении в гимназии.

По сравнению с 2009 г. общеобразовательные школы-интернаты среднего (полного) общего образования, в т.ч. с углубленным изучением отдельных предметов ухудшили свои показатели.

II. ПОДГОТОВКА ЭКСПЕРТОВ И ОСОБЕННОСТИ ПРОВЕРКИ РАБОТ ГИА-2010г.

2.1. Подготовка членов предметной комиссии. Для проверки работ по математике в новой форме были подготовлены эксперты в количестве 81 человека, в том числе 42 учителя высшей квалификационной категории, 6 учителей первой квалификационной категории общеобразовательных учреждений, 26 преподавателей высших учебных заведений. Полный курс подготовки к проверке работ ГИА по математике прошли в апреле-мае 2010 года 79 экспертов. В проверке работ ГИА по математике 2010 года приняли участие 77 членов экспертной комиссии.

2.2. Состав комиссии

Таблица 4

Количество

Процент

Преподаватели учреждений профессионального образования

32,5

Учителя

67,5

Процентное соотношение кандидатов и докторов наук (от общего количества экспертов (таблица 2)

Таблица 5

Количество

Процент

Доктора наук

Кандидаты наук

2.3. Использованная модель проверки. Для проверки заданий части 2 (С) была взята за основу модель 1, то есть та же, что и в прошлом году.

Общие подходы к формированию критериев оценивания. Согласно «Методическим рекомендациям для экспертов территориальных предметных комиссий по проверке выполнения заданий с развернутым ответом экзаменационных работ выпускников IX классов общеобразовательных учреждений. Государственная (итоговая) аттестация выпускников IX классов общеобразовательных учреждений (в новой форме), изд-во ФИПИ, 2010», требования к выполнению заданий с развернутым ответом заключаются в следующем: решение должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений обучающегося. Оформление решения должно обеспечивать выполнение указанных требований, а в остальном может быть произвольным. Не следует требовать от учащихся слишком подробных комментариев (например, описания алгоритмов). Лаконичное решение, не содержащее неверных утверждений, все выкладки которого правильны, следует рассматривать как решение без недочетов.

Если решение ученика удовлетворяет этим требованиям, то ему выставляется полный балл, которым оценивается это задание: № 17 – 2 балла, № 18 и 19 – 3 балла, № 20 и 21 – 4 балла. Если в решении допущена описка или ошибка, не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая, несмотря на ее наличие, сделать вывод о владении материалом, то учащемуся засчитывается балл, на 1 меньший указанного.

Ниже описаны некоторые общие позиции, являющиеся основанием для выставления сниженного на единицу балла.

Задание 17 (2 балла). За решение выставляется 1 балл, если оно не содержит ошибок, но при этом не является полным, например, отсутствует ответ на дополнительный вопрос (при его наличии); или в решении имеется одна описка/ошибка, не влияющая принципиально на ход решения, с ее учетом все дальнейшие шаги выполнены верно, решение доведено до конца.

Задания 18 и 19 (3 балла). За решение выставляется 2 балла, если в нем нет ошибок, но при этом оно не является полным, например, отсутствует ответ на дополнительный вопрос (при его наличии); или ход решения верный, получен ответ, но имеется описка или непринципиальная ошибка (например, ошибка в вычислении), и с ее учетом дальнейшие шаги выполнены верно, решение доведено до конца.

Задания 20 и 21 (4 балла). За решение выставляется 3 балла, если решение «почти верное», т.е. ход решения правильный, оно доведено до конца, но при этом имеется одна непринципиальная вычислительная ошибка/описка, с ее учетом дальнейшие шаги выполнены верно; или имеются погрешности в применении символики и терминологии.

В критериях оценивания по каждому конкретному заданию второй части экзаменационной работы эти общие позиции конкретизируются и пополняются с учетом содержания задания. Критерии разработаны применительно к одному из возможных решений, а именно к тому, которое описано в рекомендациях. При наличии в работах учащихся других решений критерии вырабатываются предметной комиссией с учетом описанных общих подходов. Решения учащихся могут содержать недочеты, не отраженные в критериях, но которые, тем не менее, позволяют оценить результат выполнения задания положительно (со снятием одного балла). В подобных случаях решение о том, как квалифицировать такой недочет, принимает предметная комиссия. При проверке и оценке экзаменационных работ не учитываются особенности почерка и наличие грамматических ошибок в работах учащихся, если они не искажают сути ответа.

Другие возможности в этой модели не предусмотрены. Такой подход в методике оценки выполнения заданий третьей части связан с трактовкой качественных свойств, на измерение которых она направлена: способность к интеграции знаний из различных разделов курса алгебры, владение широким арсеналом приемов и способов рассуждений, умение математически грамотно и ясно записать решение. Исследуемые качества проявляются, только если учащийся обнаруживает умение решить задачу предложенного уровня и содержания. Поэлементное оценивание выполнения задания не дает возможности оценить именно эти качества и отразить их наличие у учащегося в его интегральной оценке. Кроме того, для проверки владения отдельными элементами содержания служат задания первой части работы.

В этом году предметная комиссия Иркутской области, учтя весь опыт проведения итоговой аттестации в 9-х классах, посчитала возможным в соответствии с федеральным стандартом увеличить время на выполнение части 1. В 2010 году на выполнение первой части работы (частей А и В) обучающемуся отводилось 90 минут, при этом для получения положительной отметки учащемуся по-прежнему (в соответствии с федеральным стандартом) было необходимо решить правильно не менее 8 заданий из всех 16 заданий части 1. Указанный порог (8 заданий из 16) принимается за минимальный критерий соответствия подготовки ученика уровню обязательных требований. Если учащийся не подтверждает наличия у него базовой подготовки, то это является основанием для выставления ему неудовлетворительной отметки. В этом случае результат учащегося не компенсируется выполнением заданий второй части, рейтинг не указывается.

При положительной оценке работы ученику выставляется два количественных показателя: отметка «3», «4» или «5» и рейтинг. Ниже приведено соотношение рейтинговых интервалов и отметок по 5-балльной шкале:

Таблица 6

Схема перевода общего балла в отметки по 5-балльной шкале

Общий балл

Выполнено менее 8 заданий в части 1 (менее 8 баллов за часть 1)

При выполнении минимального критерия

8 – 14 баллов

15 – 21 балла

22 – 32 балла

Отметка

«2»

«3»

«4»

«5»

Диапазон выставления каждой из положительных отметок достаточно широк, причем наиболее широким он является для отметки «5». Это соответствует поставленной задаче более детальной дифференциации учащихся с высоким уровнем подготовки, что становится еще более актуальным при реальном существовании классов с разным количеством часов на обучение математике (от 5 до 8 уроков в неделю), введении в 9-х классах предпрофильной подготовки.

III. ХАРАКТЕРИСТИКА КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛОВ (ДАЛЕЕ - КИМ) ГИА В НОВОЙ ФОРМЕ
ПО МАТЕМАТИКЕ В 2010 г.

3.1. Цель экзаменационной работы – государственная (итоговая) аттестация по математике выпускников девятых классов общеобразовательных учреждений на основе оценки уровня овладения обучающимися программным материалом, соответствующим требованиям государственных образовательных стандартов. Работа рассчитана на выпускников 9-х классов общеобразовательных учреждений (школ, гимназий, лицеев), включая классы с углубленным изучением математики. Результаты экзамена могут быть использованы при комплектовании профильных десятых классов, а также при приеме в учреждения системы начального и среднего профессионального образования без организации дополнительных испытаний.

Кодификатор экзаменационной работы соответствует обязательному минимуму содержания (приложение к Приказу Минобразования №1236 от 19.05.98) В 2010 г. при составлении работ используется кодификатор, разработанный Федеральным Институтом Педагогических Измерений (ФИПИ).

Содержание экзаменационных заданий по математике находится в рамках содержания образования, обозначенного «Федеральным компонентом государственного стандарта общего образования. Математика. Основное общее образование; 2004».

В 2010 г. предлагаются две демоверсии экзаменационной работы. Первая по своим общим подходам не отличается от работ 2009 г., вторая в части 1 дополнительно содержит два задания по разделу вероятность и статистика. В Иркутской области в 2010 г. была использована Версия 1. С 2011 г. будет использоваться Версия 2.

3.2. Распределение заданий по частям экзаменационной работы

Таблица 7

№ п/п

Части работы

Число заданий

Максимальный первичный балл

% максимального первичного балла за данную часть работы от общего максимального балла

Тип заданий

Часть 1(А)

Задания с

выбором

ответа

Часть 1(В)

Задания с

кратким

ответом

Часть 2(С)

Задания с

развернутым

ответом

Итого

100%

Все типы

3.3. Анализ структуры КИМ 2010 года

Общая характеристика работы.

Работа состоит из двух частей. Часть 1 направлена на проверку овладения содержанием курса на уровне базовой подготовки. По версии 1 она содержит 16 заданий, в совокупности охватывающих следующие разделы курса: числа, буквенные выражения, преобразования алгебраических выражений, уравнения, неравенства, последовательности и прогрессии, функции и графики. По версии 2 первая часть работы содержит 18 заданий за счет включения в проверку (дополнительно к указанным выше) раздел вероятность и статистика. Задания расположены группами в соответствии с разделами содержания, к которым они относятся.

В первой части работы проверяется владение базовыми алгоритмами, знание и понимание важных элементов содержания (понятий, их свойств, приемов решения задач и пр.), умение применить знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применение знаний в простейших практических ситуациях. При выполнении заданий первой части учащиеся должны продемонстрировать умение пользоваться различными математическими языками, определенную системность знаний и широту представлений.

Часть 1 подразделяется на части 1(А) и 1(В). Часть 1(А) содержит 8 заданий и часть 1(В) – 8 заданий, в совокупности охватывающих все разделы курса и предусматривающих три формы ответа: задания с выбором ответа из четырех предложенных вариантов (8 заданий части 1(А)), задания с кратким ответом (7 заданий части 1(В)) и 1 задание на соотнесение в части 1(В).

При выполнении заданий первой части учащиеся должны продемонстрировать определенную системность знаний и широту представлений. В них проверяется не только владение базовыми алгоритмами, но и знание и понимание важных элементов содержания (понятий, их свойств, приемов решения задач и пр.), умение пользоваться различными математическими языками, умение применить знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применение знаний в простейших практических ситуациях. Иными словами, по сравнению с традиционной практикой в первой части работы усилены идейно-понятийная и практическая составляющие.

Основными условиями, которым должна удовлетворять эта часть работы, являются реалистичность предъявляемых учащимся требований и обеспечение полноты проверки на базовом уровне. В основу их структурирования положен содержательный принцип – задания расположены группами в соответствии с разделами содержания, к которым они относятся.

Часть 2 направлена на проверку владения материалом на повышенном и высоком уровнях. Основное ее назначение – дифференцировать хорошо успевающих школьников по уровням подготовки. В этой части работы содержится 5 заданий разного уровня сложности, требующих развернутого ответа (с записью решения). Все пять заданий представляют разные разделы содержания. Каждое из них относится к одному из следующих семи разделов: выражения и их преобразования; уравнения; неравенства; функции; координаты и графики; арифметическая и геометрическая прогрессии; текстовые задачи.

Все задания этой части носят комплексный характер. Они позволяют проверить владение формально-оперативным алгебраическим аппаратом, способность к интеграции знаний из различных тем школьного курса, владение достаточно широким набором приемов и способов рассуждений, а также умение математически грамотно записать решение.

Задания во второй части расположены по нарастанию сложности – от относительно простой задачи до задач достаточно сложных, требующих свободного владения материалом курса и высокого уровня математического развития. Фактически при этом во второй части работы представлены три разных уровня. Первое задание (задание 17 в экзаменационной работе) самое простое. Как правило, оно направлено на проверку владения формально-оперативными навыками: преобразование выражения, решение уравнения, неравенства, системы, построение графика. По уровню сложности это задание лишь немногим превышает обязательный уровень.

Следующие два задания (задания 18 и 19 экзаменационной работы) более высокого уровня, они сложнее первого и в техническом, и в логическом отношении. При хорошем выполнении первой части правильное решение этих заданий уже обеспечивает получение «пятерки».

И, наконец, последние два задания (задания 20 и 21) – наиболее сложные, они требуют свободного владения материалом и довольно высокого уровня математического развития. Рассчитаны эти задачи на выпускников, изучавших математику более основательно, чем в рамках пятичасового курса, – это, например, углубленный курс математики, элективные курсы в ходе предпрофильной подготовки, математические кружки и пр. Хотя эти задания не выходят за рамки содержания, предусмотренного стандартом основной школы, при их выполнении выпускник имеет возможность продемонстрировать владение довольно широким набором некоторых специальных приемов (выполнения преобразований, решения уравнений, систем уравнений), проявить некоторые элементарные умения исследовательского характера.

Содержание экзамена находится в рамках «Обязательного минимума содержания основного общего образования по математике» (Приказ Минобразования от 19.05.1998 №1276). Новые вопросы, предусмотренные образовательным стандартом 2004 г. («Элементы комбинаторики, статистики и теории вероятностей»), на данном этапе в работе не представлены. Одновременно в экзаменационных работах отражены идейные изменения, вносимые образовательным стандартом 2004 г., в требования к математической подготовке учащихся.

Структура работы отвечает цели построения системы дифференцированного обучения в современной школе, которая включает две задачи: формирование у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования; одновременное создание условий для соответствующей части школьников с целью получения подготовки повышенного уровня, достаточной для активного использования математики в дальнейшем обучении, прежде всего, при изучении ее в старших классах на профильном уровне.

Распределение заданий по разделам содержания, по видам познавательной деятельности, по видам проверяемых умений и по уровню сложности

Характеристика заданий работы. Каждое из шестнадцати заданий первой части характеризуется четырьмя параметрами: содержание, категория познавательной области, уровень трудности, форма ответа.

Содержание. Для обеспечения достаточной детализации общего плана экзаменационной работы арифметико-алгебраические блоки «Обязательного минимума содержания основного общего образования» разбиты на более мелкие разделы: (1.1.) числа, (1.2) буквенные выражения, (1.3) преобразования алгебраических выражений, (1.4) уравнения, (1.5) неравенства, (1.6) последовательности и прогрессии, (1.7) функции и графики. С 2011 г. в Иркутской области этот список будет дополнен разделом (1.8) комбинаторика, элементы теории вероятностей и статистики.

В первой части работы представлены все перечисленные разделы, причем число заданий по каждому из них примерно соответствует удельному весу этого раздела в школьном курсе. Это обеспечивает репрезентативность первой части работы, полноту проверки подготовки выпускников на базовом уровне. Распределение заданий по указанным разделам приведено в таблице 8.

Таблица 8

Распределение заданий первой части по разделам содержания

Числа (1.1)

Буквенные выражения (1.2)

Тождественные

преобразования

(1.3)

Уравнения (1.4)

Неравенства

(1.5)

Последоват.

и прогрессии

(1.6)

Функции и

графики (1.7)

Всего

Категории познавательной области. «Требования к уровню подготовки выпускников», задаваемые образовательными стандартами 2004 г., распределяются по трем рубрикам: знать/понимать, уметь, применять полученные знания в практических ситуациях. При разработке операциональных критериев успешности усвоения курса алгебры на базовом уровне, в силу особенностей и специфики этого предмета, категория «уметь» подразделена на два блока: умение действовать в соответствии с известным алгоритмом (правилом, планом, приемом) и умение решить математическую задачу, не сводящуюся к прямому применению алгоритма.

В соответствии с этим, каждое задание первой и второй частей экзаменационной работы соотносится с одной из четырех категорий познавательной области: знание/понимание, умение применить алгоритм (далее – алгоритм), умение применить знания для решения математической задачи (далее – решение задачи), применение знаний в практической ситуации (далее – практическое применение).

Ниже приводится характеристика каждой из выделенных категорий применительно к базовому уровню подготовки.

Знание/понимание: владение термином; владение различными эквивалентными представлениями (например, числа); распознавание (на основе определений, известных свойств, сформированных представлений); использование различных математических языков (символического, графического, вербального), переход от одного языка к другому; интерпретация.

Алгоритм: использование формулы как алгоритма вычислений; применение основных правил действий с числами, алгебраическими выражениями; решение основных типов уравнений, неравенств, систем.

Решение задачи: задания с математическим контекстом, при решении которых требуется применение (актуализация) системы знаний, преобразование связей между известными фактами, включение известных понятий, приемов и способов решения в новые связи и отношения; распознавание стандартной задачи в измененной формулировке.

Практическое применение: задания, соответствующие одной из первых трех категорий данного списка, формулировка которых содержит практический контекст, знакомый учащимся или близкий их жизненному опыту.

Ориентировочная доля заданий, относящихся к каждой из категорий, представлена в таблице 9.

Таблица 9

Распределение заданий первой части по видам познавательной деятельности

№ п/п

Виды

проверяемых умений

Число заданий

Максимальный балл за выполнение заданий по каждому виду умений

% от общего

максимального

балла

знание/
понимание

алгоритм

43,75

решение задачи

12,5

практическое применение

18,75

Всего

100

В этом году заметен явный уклон в сторону алгоритмических навыков (в 2010 г. уровень алгоритмических навыков составлял 31,25%). Эта тенденция, на наш взгляд, облегчает работу учителей по подготовке к ГИА, но вредит дальнейшему обучению математике и подготовке к ЕГЭ, где в гораздо большей степени требуется понимание и умение решать задачи.

3.5. Распределение заданий экзаменационной работы по реальному уровню сложности

Таблица 10

Уровень сложности

заданий

(процент выполнивших задания в Иркутской области)

Число заданий

Максимальный балл

за выполнение

заданий каждого

уровня сложности

% от общего

максимального

балла

60-80%

34,375

40-60%

15,625

20-40%

9,375

15-20%

15,625

10-15%

12,5

5-10%

0,5-4%

12,5

IV. АНАЛИЗ РЕЗУЛЬТАТОВ ОСВОЕНИЯ ЭЛЕМЕНТОВ СОДЕРЖАНИЯ

СТАНДАРТА ПО МАТЕМАТИКЕ В 2010 ГОДУ

4.1. Основные статистические сведения

В Иркутской области государственная (итоговая) аттестация по математике в новой форме в 2010 году проходила в четвертый раз. В общей сложности в ней приняли участие 26572 обучающихся 9-х классов. При этом 9,2% (5,3% в 2009г.) школьников справились с работой на «отлично», 21,7 (18,0% в 2009г.) – на «хорошо», 38,2% (32,9% в 2009г.) – на «удовлетворительно», а 30,9% (43,8% в 2009г.) учащихся получили отметку «неудовлетворительно».

При этом процент работ, получивших отметку «неудовлетворительно», колебался по городским школам от 3,9% до 49,7% , а по сельским школам – от 13,3% до 65,3% .

Процент работ, получивших отметки «хорошо» или «отлично» составил в среднем по области 30,9% и колебался по городским школам от 36,6% до 19,3% , а по сельским школам – от 39,5% до 9,7% .

4.2. Характерные нарушения, выявившиеся в ходе проверки работ

ГИА-2010 по математике

Приходится констатировать, что некоторые школы и целые территории отнеслись к проведению ГИА -2010 недобросовестно. При проверке части 1 было замечено массовое зачеркивание неверных результатов и приписка верных, а при проверке части 2 решения нередко приводились как под копирку. Вот характерные нарушения в ходе ГИА-2010:

Работы всех 4-х вариантов решены «под копирку», с одинаковыми описками и ошибками (МОУ Серёдкинская СОШ Боханского района, Мамоновская СОШ Иркутского района, СОШ №73 г. Иркутска, СОШ № 14 г. Братска, ряд школ г. Зимы, …).

Все неправильные ответы в части 1 всех работ данной школы зачёркнуты, и справа другим почерком записаны верные ответы (СОШ №6 Шелеховского района,).
В значительном числе работ согласованы ответы учащихся, выполнявших одинаковые варианты.
В некоторых работах на бланках 1 или 2 не проставлен код участника или номер варианта. В этом случае проверка проводилась по фактически выполненному варианту.

Возможно, что на количество и характер нарушений повлияла задержка (до трёх суток!) с доставкой работ в РЦОИ. В частности, вызывает сомнения в авторстве учащегося одна, доставленная в РЦОИ 31 мая, работа с подробными и верными решениями части 2 (запись на трёх листах выполнена печатными буквами!), гимназия №1 г. Братска, код участника 0501.

4.3. Анализ результатов выполнения заданий части 1

Первая часть экзаменационной работы, направленная на проверку уровня базовой подготовки, включала задания по следующим содержательным блокам: числа, буквенные выражения и преобразования выражений, уравнения и неравенства, функции и графики, последовательности и прогрессии. Ниже представлены результаты выполнения заданий (в процентах).

Таблица 11

№ задания

части 1

Содержание задания

процент

выполнения

Задания с выбором ответа

1 (А1)

Оценить табличные данные

2 (А2)

Вычислить процент от числа

3 (А3)

Выявить рациональное число

6 (А4)

Преобразовать степенные выражения

8 (А5)

Найти неверное преобразование алгебраического выражения

11 (А6)

Выбрать уравнение, соответствующее условию задачи

14 (А7)

Сравнить числа на числовой прямой

15 (А8)

Указать прямую, имеющую одну общую точку с параболой

Задания с кратким ответом

4 (В1)

Найти значение выражения

5 (В2)

Составить выражение для вычисления площади

7 (В3)

Упростить выражение

9 (В4)

Решить линейное уравнение

10 (В5)

Найти координаты точки решением системы

12 (В6)

Установить соответствие прогрессий

13 (В7)

Решить квадратное неравенство

16 (В8)

По графикам движения двух групп оценить, какая группа пришла быстрее и на сколько

Как видно из приведённых данных, ГИА-2010 показала в целом средний уровень базовой математической подготовки обучающихся.

Наиболее трудными для обучающихся оказались задача 13 на решение квадратного неравенства (40%) и задача 16 на чтение графиков (44%) .

Задача 13. Решите неравенство .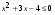

Умение решать квадратные уравнения и неравенства – это базовый элемент и всегда являлся основным и необходимым элементом для дальнейшего обучения. В старших классах почти все виды уравнений и неравенств в конечном итоге сводятся к линейным или квадратным. В этом году получился наихудший результат по этой теме. Заметим, что при решении задачи 13 многие учащиеся указывали в ответе корни уравнения, а не решения неравенства.

Задача 16. Две группы туристов – А и В вышли с турбазы «Южная» и прошли по одному и тому же маршруту до турбазы «Северная». На рисунке изображены графики их движения.

s, км

1 2 3 4 5

(Вариант 2105) Какая из двух групп затратила на прохождение маршрута больше времени и на сколько часов? (Ответ: группа В на 1 час).

(Вариант 2106) Какое расстояние прошла группа А за то время, пока группа В отдыхала на привале? (Ответ: 2 км).

(Вариант 2107) Какая из двух групп потратила меньше времени на первые 12 км пути и на сколько часов? (Ответ: группа А на 1 час).

(Вариант 2108) На каком расстоянии от турбазы «Южная» была группа В к тому моменту, когда группа А прошла 10 км? (Ответ: 6 км).

В задаче 16 во всех вариантах был один и тот же рисунок с графиками движения двух групп туристов, но вопросы в каждом варианте были разные. В вариантах 2106 и 2108 нужно было найти расстояние по графику, и с этим заданием справилось почти 62% участников. В вариантах 2105 и 2107 нужно было сравнить время движения, и с этим заданием справилось уже только 27% участников, поскольку многие не учли, что группы вышли не одновременно.

Отметим, что умение читать графики функций требовалось также и на ЕГЭ-2010 в заданиях В2 (с ним справились 92% выпускников) и В8 (с ним справились всего 33% выпускников!), а умение решать линейное уравнение (как в задании 9 части 1 ГИА-2010) требовалось также в задании В3 ЕГЭ-2010 (с ним справились 70% выпускников).

Третий снизу результат (46%) оказался при решении задачи 10, где нужно было по ходу дела решить квадратное уравнение.

Задача 10. Окружность, изображенная на рисунке, задается уравнением 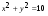, а прямая – уравнением 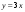. Вычислите координаты точки В. (На рисунке обозначены две точки пересечения окружности и прямой: точка А в первой четверти и точка В во второй четверти).

С квадратным уравнением справились несколько лучше, чем с квадратным неравенством. Отметим, что решить систему или совокупность квадратных неравенств требовалось и в задании 20 части 2, а задача 21 сводится к решению уравнения, приводящегося к квадратному.

4.4. Анализ результатов выполнения заданий части 2

Таблица 12

Основная статистика по выполнению заданий части 2

Порядковый

номерздания

Обозначение

задания

в работе

Проверяемые элементы

содержания
и виды

деятельности

Резуль-

таты

в %

(все)

Резуль-

таты

в %

(лицеи)

Резуль-таты

в %

(гимназии)

17 (С1)

Написать уравнение прямой,

параллельной данной прямой и проходящей через данную точку

18 (С2)

Упростить буквенное

выражение

19 (С3)

Найти значение параметра,

при котором система уравнений

имеет решение

20 (С4)

Указать все целые числа, не входящие в область

определения данной функции

21 (С5)

Текстовая задача на движение

Результаты лицеев и гимназий приведены для демонстрации успехов последних по сравнению со средними результатами по области.

Таблица 13

Сравнительный процент выполнения заданий части 2 по годам

Планируемый уровень трудности

40-60%

25-40%

8-12%

Реальный уровень трудности(2007г.)

39%

19%

18%

15%

Реальный уровень трудности(2008г.)

20%

11%

17%

Реальный уровень трудности(2009г.)

20%

10%

14%

Реальный уровень трудности(2010г.)

15%

19%

31%

Разные результаты выполнения заданий отчасти объясняются различиями в самих заданиях. Так, в задании № 17 в 2007г. требовалось построить график линейной функции, и учащиеся неплохо справились с ним. Следует заметить, что наши школьники в целом справляются с заданиями по линейным уравнениям, линейным неравенствам и системам линейных уравнений или неравенств. В 2008 г. в этом же задании уже требовалось построить график квадратичной функции, и результаты резко упали: уровень выполнения вдвое ниже планируемого. В 2009г. в задании № 17 нужно было решить систему линейных неравенств. Одно линейное неравенство или систему линейных уравнений наши учащиеся еще решают, но система неравенств уже мало кому доступна: уровень выполнения вдвое ниже планируемого. В 2010г. в этом задании нужно было записать уравнение прямой, проходящей через данную точку параллельно заданной прямой, и результат еще понизился, т.к. учащиеся плохо понимают условие параллельности прямых и геометрический смысл углового коэффициента.

Задание № 17 (2010г.). Запишите уравнение прямой, параллельной прямой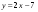

и проходящей через точку .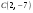

В задании № 18 в 2007г. требовалось упростить алгебраическое выражение с использованием формул сокращенного умножения и учащиеся неплохо (но ниже планируемого) справились с ним. В 2008 г. в этом задании требовалось выяснить, имеет ли корни квадратное уравнение, и вновь провал по этой теме: уровень выполнения втрое ниже планируемого. В 2009г. была довольно сложная задача на проценты, где нужно было сравнивать, на сколько процентов первый предмет дороже (дешевле) второго, если известно, на сколько процентов второй предмет дешевле (дороже) первого. Аналогичное задание было и в КИМах ГИА. Эта тема трудна для наших выпускников. Часто учителя однобоко подходят к изучению этой темы, применяя, в основном, метод пропорций. В 2010г. в задании № 18, как и в 2007г., требовалось упростить алгебраическое выражение с использованием формул сокращенного умножения, и результат практически совпал с 2007г.

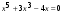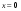В задании № 19 в 2007г. была дана задача на прогрессии, и учащиеся справились ниже среднего. В 2008 г. была задача на проценты и составление простейших уравнений: уровень выполнения вдвое ниже планируемого. В 2009г. была довольно сложная задача – решить уравнение: . Если вынести за скобки и не потерять корень , то уравнение сведется к решению биквадратного уравнения. И снова эта тема провалена для наших учителей и их учеников. В 2010г. в задании № 19, требовалось решить систему двух линейных уравнений с двумя неизвестными и результат решения подставить в третье уравнение, чтобы узнать, при каком значении параметра система трех линейных уравнений с двумя неизвестными имеет решение. И с этим заданием выпускники основной школы Иркутской области справились как должно, а выпускники лицеев и гимназий значительно превысили планируемый уровень.

В задании № 20 в 2007г. была задача с параметром. Требовалось узнать, при каких значениях параметра прямая пересекает параболу в двух точках, т.е., опять нужно было знать, когда квадратное уравнение имеет два корня. В 2007г. учащиеся справились с этим заданием даже неплохо. В 2008 г. была задача с параметром на использование теоремы Виета для корней квадратного уравнения, составление и решение системы уравнений. Уровень выполнения упал вдвое. В 2009г. была задача с параметром, в которой нужно было найти, при каких значениях параметра квадратное неравенство 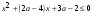не имеет решений. Сразу три проблемных темы: параметры, квадратное неравенство и расположение параболы. Результат втрое ниже планируемого. В 2010г. в задании № 20 требовалось указать все целые числа, не принадлежащие области определения данного выражения.

Задание № 20 (2010г.). Укажите все целые числа, которые не принадлежат

области определения выражения .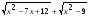

Можно было найти область определения выражения, решив систему квадратных неравенств, а затем выбрать целые числа и дополнения, либо сразу решить совокупность квадратных неравенств противоположного знака и выбрать целые числа из полученного множества. Следует отметить, что учащиеся и 9-х, и 11-х классов плохо решают системы, и, в особенности, совокупности неравенств; путают объединение с пересечением, не видят объединение двух интервалов. Однако в этом году с этим сложным заданием наши участники ГИА справились как должно, а выпускники лицеев и гимназий значительно превысили планируемый уровень. Справедливости ради следует отметить, что сравнительно высокие показатели по заданию 20 достигнуты в 2010 году во многом за счёт неудачной, на наш взгляд, формулировки критериев оценивания данного задания. А именно: расплывчатую фразу «допущена ошибка на последнем шаге при нахождении пересечения множеств …» следовало бы заменить на вполне конкретную: «установлено, с точностью до конечного числа точек, множество всех вещественных чисел, не принадлежащих области определения данного выражения …».

В задании № 21 в 2007г. была стандартная текстовая задача на движение, и учащиеся справились с ней на планируемом уровне. В 2008 г. была задача на вычисление числового значения выражения с радикалами: 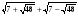, где нужно было догадаться и правильно возвести в квадрат данное выражение, предварительно оценив его знак. Догадались всего 1,7% - много ниже планируемого. В 2009г. была довольно сложная задача на выделение полных квадратов очень важное и полезное (для построения графика, для нахождения вершины параболы) умение. И снова эта тема провалена нашими учителями и обучающимися. Как видим по результатам (0,55%), этим умением наши школьники не владеют. В 2010г. в задании № 21 требовалось решить довольно сложную задачу на движение. Эта задача на составление уравнения оказалась самой сложной. Она по содержанию даже сложнее, чем задача В12 (с указанием лишь правильного ответа) из ЕГЭ 2010г., а по виду уравнения идентична ей. Кроме того, девятиклассники должны были представить решение, с чем справились лишь 1,4% (хотя гораздо больше участников угадали правильный ответ).

Задание № 21 (2010г.). Из деревни в одном направлении выехали 3 велосипедиста с интервалом в 1 час. Первый едет со скоростью 15 км/ч, а второй со скоростью 20 км/ч. Третий велосипедист догоняет первого, а еще через час догоняет второго. Найдите скорость третьего велосипедиста.

Решение. Пусть км/ч – скорость третьего велосипедиста. Тогда скорость сближения третьего с первым равна 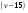, а со вторым равна 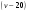. В момент выезда третьего велосипедиста первый находился от него на расстоянии 30 км, а второй – 20 км. Составим уравнение: 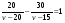. Из двух корней получившегося квадратного уравнения подходит лишь один: . Ответ: скорость третьего велосипедиста равна 25 км/ч.

Большинство обучающихся, решавших эту задачу, неверно поняли условие и считали, что третий догоняет первого также через час, и тогда подбором удавалось найти правильный ответ. Такое решение оценивалось, конечно, в 0 баллов.

Таблица 14

Сравнительный процент выполнения заданий части 2

по образовательным учреждениям

№ задания

Вид ОУ

Планируемый уровень трудности

40-60%

25-40%

8-12%

Лицеи и лицей-интернат

Реальный уровень трудности

44%

54%

73%

34%

11%

Гимназия

29%

42%

60%

25 %

СОШ с углубленным изучением предмета

21%

32%

47%

19%

СОШ

13%

15%

29%

Основные ОШ

16%

23%

0,2%

ВСОШ и ОСОШ

0,4%

0,1%

Центры образования

10%

16%

24%

0,5%

Все

15%

19%

31%

Из приведённых данных видно, что реальный уровень трудности (реальный процент правильно выполненных заданий по области в целом) оказался ниже планируемого по заданиям 17, 18, 21, а по заданиям 19 и 20 – в пределах планируемого. При этом результаты по всем заданиям, кроме С1, выше, чем были в прошлом году.

Как видим из таблицы 14, по задачам 17 и 21 только лицеисты уложились в планируемый уровень трудности, а по задачам 18, 19 и 20 лицеисты значительно, как и должно быть, превысили планируемый показатель. Гимназисты также справились с заданиями вдвое лучше, чем в среднем. Показатели всех остальных категорий выпускников ниже планируемого уровня.

4.5. Рекомендации

1) На всех этапах проведения ГИА-2011 всем организаторам необходимо строго следовать инструкциям по проведению ГИА. В случае нарушения инструкций по организации и проведению ГИА предметная комиссия оставляет за собой право не проверять соответствующие работы.

2) Рекомендуем уделить первостепенное внимание выполнению заданий базового уровня. Особое внимание следует обратить на решение квадратных уравнений и неравенств.

3) Необходимо в течение учебного года обеспечить обучающимся возможность тренировочного тестирования на местах с тем, чтобы не допускать во время проведения ГИА потери баллов по техническим причинам.

4) Следует особо иметь в виду, что в программу ГИА по математике в 2011 году войдут также элементы комбинаторики, теории вероятностей и статистики.

5) При подготовке к экзамену помимо учебников, по которым ведется преподавание, рекомендуется использовать следующие издания:

1. Новые формы проведения государственной (итоговой) аттестации учащихся 9 классов.

Сборник нормативно-правовых и инструктивно-методических материалов/

Сост. А.Г. Капустняк и др.– Москва, 2004.

2. Комплект методических материалов, обеспечивающих проведение государственной (итоговой) аттестации учащихся 9 классов общеобразовательных учреждений в новых формах Сборник нормативно-правовых и инструктивно-методических материалов/

Сост. Л.О. Рослова, Л.М. Рыбченкова.– М.: Просвещение, 2005.

3. Алгебра. Сборник заданий для подготовки к итоговой аттестации в 9 классе/

Л.В.Кузнецова и др.– М.: Просвещение, 5-е издание, 2010.

4. Алгебра. 9 класс. Подготовка к итоговой аттестации/ под ред Ф.Ф.Лысенко

– Ростов-на-Дону: изд-во «Легион», 2008.

В изданиях [1] и [2] помимо нормативно-правовой и инструктивно-методической информации содержатся демонстрационные версии и тексты экзаменационных работ за прошлые годы. С экзаменационными работами 2006-2010 гг., а также с соответствующими результатами можно познакомиться на сайтах http://ege.edu.ru , http://www.fipi.ru, http://obrnadzor.gov.ru. Полезную информацию можно также найти в статьях, опубликованных в журнале «Математика в школе» (№1/2006), в газете «Математика» («Первое сентября») (№23/2005, №9/2006, №1/2007).

В издании [3] содержится, как правило, весь спектр возможных на экзамене по математике заданий как части 1, так и части 2. Так, задания 13 из вариантов ГИА-2010 такие же, как задания 13 на стр. 17 и 21 издания [3]. Задания 16 из вариантов ГИА-2010 такие же , как задания 16 на стр. 50 и 54 издания [3]. Задания С1 из вариантов ГИА-2010 такие же, как задания 6.2 на стр. 138 издания [3]. Задания С2 из вариантов ГИА-2010 такие же, как задание 1.33 на стр. 109 издания [3]. Задания С3 из вариантов ГИА-2010 такие же, как задание 3.25 на стр. 120 издания [3]. Задания С4 из вариантов ГИА-2010 подобны заданиям 4.22 и 4.23 на стр. 125 издания [3]. Задания С5 из вариантов из вариантов ГИА-2010 такие же, как задание 8.29 на стр. 162 издания [3].

Отметим, что в издание [3] уже включены типовые задания ГИА-2011 с элементами комбинаторики, теории вероятностей и статистики (см. Приложение 2, стр. 221-238).

результатЫ
ГОСУДАРСТВЕННОЙ (ИТОГОВОЙ) АТТЕСТАЦИИ ВЫПУСКНИКОВ 9-Х КЛАССОВ

В НОВОЙ ФОРМЕ

математика

ВЫПУСК 13

Методические рекомендации