работа по дисциплине "Прикладная математика"
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
КУРСОВАЯ РАБОТА
по дисциплине "Прикладная математика"
14 вариант
Выполнил: Рудковский Ф.А.
Москва 2004
ОГЛАВЛЕНИЕ
ЛИНЕЙНАЯ ПРОИЗВОДСТВЕННАЯ ЗАДАЧА
Предприятие может выпускать четыре вида продукции, используя для этого три вида ресурсов. Известна технологическая матрица А затрат любого ресурса на единицу каждой продукции, вектор В объемов ресурсов и вектор С удельной прибыли
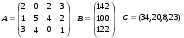 (1)
(1)
Требуется составить производственную программу (x1, x2, x3, x4), максимизирующую прибыль
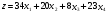 (2)
(2)
при ограничениях по ресурсам: 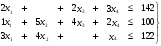 (3)
(3)
Получили задачу на условный экстремум. Для ее решения систему неравенств (3) при помощи дополнительных неотрицательных неизвестных х5, х6, х7 заменим системой линейных алгебраических
уравнений 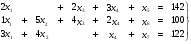 (5)
(5)
где дополнительные переменные имеют смысл остатков соответствующих ресурсов. Среди всех решений системы уравнений (5), удовлетворяющих условию неотрицательности х10, х20,… ,х50,…, х70. (6)
надо найти то решение, при котором функция (2) примет наибольшее значение.
Воспользуемся тем, что правые части всех уравнений системы (5) неотрицательны, а сама система имеет предпочитаемый вид – дополнительные переменные являются базисными. Приравняв к нулю свободные переменные х1, х2, х3, х4, получаем базисное неотрицательное решение
первые четыре компоненты которого определяют производственную программу x1=0, x2=0, x3=0, x4=0 (8)
по которой мы пока ничего не производим. Из выражения (2) видно, что наиболее выгодно начинать производить продукцию первого вида, так как прибыль на единицу продукции здесь наибольшая. Чем больше выпуск в этой продукции, тем больше прибыль. Выясним, до каких пор наши ресурсы позволяют увеличить выпуск этой продукции. Для этого придется записать для системы уравнений (5) общее решение
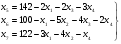 (9)
(9)
Мы пока сохраняем в общем решении х2=х3=х4=0 и увеличиваем только х1. При этом значения базисных переменных должны оставаться неотрицательными, что приводит к системе неравенств
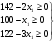 или
или 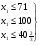 т.е. 0 х1
т.е. 0 х1 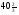
Дадим х1 наибольшее значение х1 = , которое она может принять при нулевых значениях других свободных неизвестных, и подставим его в (9). Получаем для системы уравнений (5) частное неотрицательное решение:
, которое она может принять при нулевых значениях других свободных неизвестных, и подставим его в (9). Получаем для системы уравнений (5) частное неотрицательное решение:
х1= , х2=0, х3=0, х4=0; x5=
, х2=0, х3=0, х4=0; x5= ; x6=
; x6= ; x7=0 (10)
; x7=0 (10)
Нетрудно убедиться, что это решение является новым базисным неотрицательным решением системы линейных алгебраических уравнений (5), для получения которого достаточно было принять в системе (5) неизвестную х1 за разрешающую и перейти к новому предпочитаемому виду этой системы, сохранив правые части уравнений неотрицательными, для чего за разрешающее уравнение мы обязаны принять третье, так как
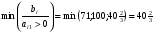 , а разрешающим элементом будет а31=3.
, а разрешающим элементом будет а31=3.
Остается заметить, что процесс решения обычно записывается в виде некоторой таблицы 1.
~
С
34 20 8 23 0 0 0
Базис
Н
x1 x2 x3 x4 x5 x6 x7
Пояснения
0
Х5
142
2 0 2 3 1 0 0
z0 = 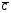 H
H
0
Х6
100
1 5 4 2 0 1 0
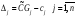
0
Х7
122
3 4 0 1 0 0 1
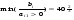
z0 -z
0 - z
-34 -20 -8 -50 0 0 0
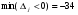
0
Х5
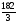
0 -8/3 2 7/3 1 0 -2/3
min (26; 35,6;122)=26
0
Х6
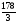
0 11/3 4 5/3 0 1 -1/3
34
Х1
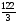
1 4/3 0 1/3 0 0 1/3
z0 -z
4148/3-z
0 76/3 -8 -35/3 0 0 34/3
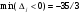
23
Х4
26
0 -8/7 6/7 1 3/7 0 -2/7
0
Х6
16
0 39/7 18/7 0 -5/7 1 1/7
34
Х1
32
1 12/7 -2/7 0 -1/7 0 3/7
z0 -z
1686-z
0 12 2 0 5 0 8
все j 0
Используя формулы исключения получаем для системы уравнений (5) новый предпочитаемый эквивалент и новую вспомогательную систему:
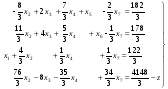 (11)
(11)
Первые три уравнения этой системы представляют некоторый предпочитаемый эквивалент системы уравнений (5) и определяют базисное неотрицательное решение (10) и производственную программу х1=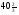 , х2=0, х3=0, х4=0, а из последнего уравнения системы (11) получается выражение функции цели через свободные переменные:
, х2=0, х3=0, х4=0, а из последнего уравнения системы (11) получается выражение функции цели через свободные переменные:
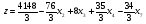
Очевидно, если имеется хотя бы один отрицательный коэффициент j при какой-нибудь переменной xj в последнем уравнении системы (11), то производственная программа не является наилучшей и можно далее продолжать процесс ее улучшения. Мы нашли в последнем уравнении системы (11) наименьший отрицательный коэффициент min(j<0) = -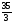 = 4. Поэтому принимаем х4 в системе (11) за разрешающую неизвестную, находим разрешающее уравнение по
= 4. Поэтому принимаем х4 в системе (11) за разрешающую неизвестную, находим разрешающее уравнение по 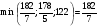 (12)
(12)
и исключаем х4 из всех уравнений системы (11), кроме первого уравнения. Укажем разрешающий элемент а14= 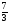 .
.
Преобразуем вспомогательную систему (11), по формулам исключения.
та система преобразуется к виду
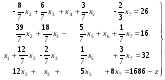 (13)
(13)
Первые три уравнения системы (13) представляют некоторый предпочитаемый эквивалент системы уравнений (5) и определяют базисное неотрицательное решение системы условий рассматриваемой задачи
x1=32, x2=0, x3=0, x4=26, x5=0, x6=16, x7=0 (14)
т.е. определяют производственную программу x1=32, x2=0, x3=0, x4=26 (15)
и остатки ресурсов:
первого вида х5=0
второго вида х6=16 (16)
третьего вида х7=0
Последнее уравнение системы (13) мы получаем, исключая х4. В последнем уравнении системы (13) среди коэффициентов при неизвестных в левой части уравнения нет ни одного отрицательного. Если из этого уравнения выразить функцию цели z через остальные неотрицательные переменные
z = 1686 - 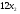 - 2x3 - 5x5 - 8 x7 (17)
- 2x3 - 5x5 - 8 x7 (17)
то становится совершенно очевидным (в силу того, что все xj0), что прибыль будет наибольшей тогда, когда
x2=0, x3=0, x5=0, x7=0 (18)
Это означает, что производственная программа (15) является наилучшей и обеспечивает предприятию наибольшую прибыль zmax = 1686 (19)
Проверим соотношение H=Q-1B
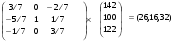
Итак, организовав направленный перебор базисных неотрицательных решений системы условий задачи, мы пришли к оптимальной производственной программе и указали остатки ресурсов, а также максимальную прибыль.
Следует обратить внимание на экономический смысл элементов последней строки последней симплексной таблицы. Например, коэффициент 2=12 при переменной х2 показывает, что если произвести одну единицу продукции третьего вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 12 единиц.
Воспользуемся тем, что в оптимальной производственной программе x2=0, x3=0. Предположим, что четвертую и третью продукции мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранив их нумерацию. Математическая модель задачи будет выглядеть следующим образом:
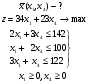
ДВОЙСТВЕННАЯ ЗАДАЧА
Ранее мы рассмотрели конкретную линейную производственную задачу по выпуску четырех видов продукции с использованием трех видов ресурсов по заданным технологиям.
Теперь представим себе, что знакомый предприниматель П, занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у1 рублей за каждую единицу первого ресурса, у2 руб. – второго, у3 руб. – третьего. Возникает вопрос: при каких ценах у1, у2, у3 мы можем согласиться с предложением П.
Величины у1, у2, у3 принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.
Напомним, что в нашей задаче технологическая матрица А, вектор объемов ресурсов В и вектор удельной прибыли С имели вид 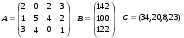
Для производства единицы продукции первого вида мы должны затратить, как видно из матрицы А, 2 единицы ресурса первого вида, 1 единицу ресурса второго вида и 3 единицы третьего (элементы первого столбца матрицы). В ценах у1, у2, у3 наши затраты составят 2у1 + 1у2 + 3у3, т.е. столько заплатит предприниматель П за все ресурсы, идущие на производство единицы продукции первого вида. На рынке за единицу первой продукции мы получили бы прибыль 34 руб. Следовательно, мы можем согласиться с предложением П только в том случае, если он заплатит не меньше 2у1 + 1у2 + 3у3 34.
Аналогично, для трех оставшихся видов продукции:
+ 5у2 + 4у320
2у1 + 4у2 8
3у1 + 2у2 + 1у323
Учтем, что за все имеющиеся у нас ресурсы нам должны заплатить 142у1 + 100у2 + 122у3 рублей. При поставленных нами условиях предприниматель П будет искать такие значения величин у1, у2, у3, чтобы эта сумма была как можно меньше. Подчеркнем, что здесь речь идет не о ценах, по которым мы когда-то приобретали эти ресурсы, а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке.
Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок у(у1, y2, y3) минимизирующий общую оценку всех ресурсов f = 142у1 + 100у2 + 122у3 (1)
при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции
2у1 + 1у2 + 3у3 34
+ 5у2 + 4у3 20 (2)
2у1 + 4у2 8
3у1 + 2у2 + 1у3 23
причем оценки ресурсов не могут быть отрицательными y1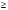 0, y2
0, y2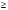 0, y3
0, y3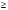 0. (3)
0. (3)
Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений 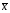 (х1, х2, х3, х4) и
(х1, х2, х3, х4) и 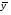 (y1, y2, y3) пары двойственных задач необходимо и достаточно выполнение условий
(y1, y2, y3) пары двойственных задач необходимо и достаточно выполнение условий
x 1 (2у1 + у2 + 3у3 - 34) = 0 y1 (2x1 + 2x3 + 3x4 - 142) = 0
x 2 ( 5у2 + 4у3- 20) = 0 y2 ( x1 +5x2 + 4x3 + 2x4 - 100) = 0
x 3 (2у1 + 4у2 - 8) = 0 y3 (3x1 +4x2 + x4- 122) = 0 .
x 4 (3у1 + 2у2 + у3 - 23) = 0
Ранее было найдено, что в решении исходной задачи х1>0, x4>0. Поэтому
2y1 + y2 + 3y3 - 34 = 0
3y1 + 2y2 + y3 - 23 = 0
Если же учесть, что второй ресурс был избыточным и, согласно той же теореме двойственности, ее двойственная оценка равна нулю у2=0,
то приходим к системе уравнений
2y1 + 3y3 - 34 = 0
3y1 + y3 - 23 = 0
откуда следует у1=5, у3=8.
Таким образом, получили двойственные оценки ресурсов у1=5; у2=0; у3=8, (4)
причем общая оценка всех ресурсов равна 1686.
Заметим, что решение (4) содержалось в последней строке последней симплексной таблицы исходной задачи. Важен экономический смысл двойственных оценок. Например, двойственная оценка третьего ресурса у3=8 показывает, что добавление одной единицы третьего ресурса обеспечит прирост прибыли в 8 единицы.
ЗАДАЧА О "РАСШИВКЕ УЗКИХ МЕСТ ПРОИЗВОДСТВА"
При выполнении оптимальной производственной программы первый и третий ресурсы используются полностью, т.е. образуют узкие места производства. Будем их заказывать дополнительно. Пусть T(t1,t2,t3)- вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться услови
H + Q-1T 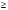 0.
0.
Задача состоит в том, чтобы найти вектор T (t1, 0, t3), максимизирующий суммарный прирост прибыли W = 5t1 + 8t3 (1) при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы)
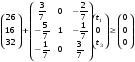 (2)
(2)
предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида 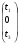
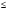
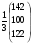 (3)
(3)
причем по смыслу задачи t1 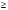 0, t3
0, t3 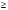 0. (4)
0. (4)
Переписав неравенства (2) и (3) в виде:
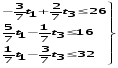 (5)
(5)
из условия (3) следует t1142/3, t3122/3 (6)
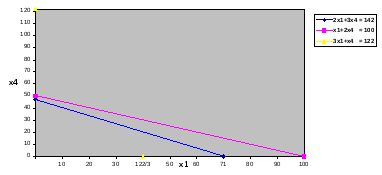
приходим к задаче ЛП: максимизировать (1) при условиях (5), (6) и (4).
Эту задачу легко решить графически: см. рис. 2.
-3/7t1+2/7t3= 26
5/7t1-1/7t3= 16
1/7t1-3/7t3 = 32
t1
t3
0
t1=142/3
t3=122/3
I
II
III
M
W
M (458/15, 122/3)
Программа расшивки имеет вид
t1=458/15, t2=0, t3=122/3 и прирост прибыли составит 5*458/15+8*122/3=478.
Сводка результатов приведена в таблице:
Cj
34 8 20 33
b
x4+i
yi
ti
aij
2 0 2 3
1 5 4 2
3 4 0 1
142
100
122
0
16
0
5
0
8
488/15
0
122/3
Xj
32 0 0 26
1686
478
j
0 12 2 0
ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Однородный продукт, сосредоточенный в 3 пунктах производства (хранения) в количествах 80; 60; 30 единиц, необходимо распределить между 4 пунктами потребления, которым необходимо соответственно 34; 40; 38; 53 единиц. Стоимость перевозки единицы продукта из пункта отправления в пункт назначения известна для всех маршрутов и равна
С = 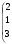
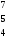
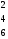
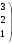 .
.
Необходимо составить план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и общие транспортные расходы по доставке продуктов были минимальными.
Для решения транспортной задачи чаще всего применяется метод потенциалов.
Общий объем производства аi =80+60+30=170 больше, чем требуется всем потребителям bi = 34+40+38+53 =165, т.е. имеем открытую модель транспортной задачи. Для превращения ее в закрытую вводим фиктивный пункт потребления с объемом потребления 170-165 = 5 единиц, причем тарифы на перевозку в этот пункт условимся считать равными нулю, помня, что переменные, добавляемые к левым частям неравенств для превращения их в уравнения, входят в функцию цели с нулевыми коэффициентами.
Первое базисное допустимое решение легко построить по правилу северо-западного угла.
Потребление
b1 =34
b2 =40
b3 =38
b4 =53
b5 =5
Производство
а1 =80
2
34
7
40
2
6
3
0
p1 = 0
a2 =60
1
5
*
4
32
2
28
0
p2 = 2
a3 =30
3
4
6
1
25
0
5
p3 = 1
q1 = 2
q2 = 7
q3 = 2
q4 = 0
q5 = -1
Общая стоимость всех перевозок для первого базисного допустимого решения:
L= 34* 2 + 40*7 + 6*2 + 32*4 + 28*2+25 =569
Обозначим через
(p1, p2,…, pm, q1, q2,…, qn)
вектор симплексных множителей или потенциалов. Тогда
Дij = Aij – cij i = (1,…,m), j = (1,…,n)
откуда следует
Дij = pi + qj– cij i = (1,…,m), j = (1,…,n) (1)
Один из потенциалов можно выбрать произвольно, так как в системе одно уравнение линейно зависит от остальных. Положим, что р1 = 0. Остальные потенциалы находим из условия, что для базисных клеток Дij = 0. В данном случае получаем
11 = 0, p1 + q1 - c11 = 0, 0+q1 -2 = 0, q1 = 2
12 = 0, p1 + q2 - c12 = 0, 0+q2 -7 = 0, q2 = 7
13 = 0, p1 + q3 - c13 = 0, 0+q3 -2 = 0, q3 = 2
23 = 0, p2 + q3 – c23 = 0, p2+2 -4 = 0, p2 = 2
24 = 0, p2 + q4 – c24 = 0, 2+q4 -2 = 0, q4 = 0
34 = 0, p3 + q4 – c34 = 0, p3+ 0 -1 = 0, p3 = 1
35 = 0, p3 + q5 – c35 = 0, 1+ q5 -0 = 0, q5 = -1
Затем по формуле (1) вычисляем оценки всех свободных клеток:
21 = p2 + q1 - c21 = 2+2-1 = 3
31 = p3 + q1 - c31 = 1+2 -3 = 0
22 = p2 + q2 – c22 = 2+7-5 = 4
32 = p3 + q2 – c32 = 1+7-4 = 4
33 = p3 + q3 – c33 = 1+2-6 = 3
14 = p1 + q4 – c13 = 0+0-3 = 3
15 = p1 + q5 – c15 = 0+(-1) = -1
25 = p2 + q5 – c25 = 2+(-1) = 1
Находим наибольшую положительную оценку max (ij > 0) = 4 = 22
Для найденной свободной клетки 22 строим цикл пересчета - замкнутую ломаную линию, соседние звенья которой взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы, одна из вершин находится в данной свободной клетке, а все остальные - в занятых клетках. Это будет 22-12-13-23. Производим перераспределение поставок вдоль цикла пересчета
40
6
40-
6+
8
38
32
32-
32
0
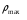 = 32
= 32
Получаем второе базисное допустимое решение:
Потребление
b1 =34
b2 =40
b3 =38
b4 =53
b5 =5
Производство
а1 =80
2
34
7
8
2
38
3
0
*
p1 = 0
a2 =60
1
5
32
4
2
28
0
p2 = -2
a3 =30
3
4
6
1
25
0
5
p3 = -3
q1 = 2
q2 = 7
q3 = 2
q4 = 4
q5 = 3
Находим новые потенциалы, новые оценки.
11 = 0, p1 + q1 - c11 = 0, 0+q1 -2 = 0, q1 = 2
12 = 0, p1 + q2 - c12 = 0, 0+q2 -7 = 0, q2 = 7
13 = 0, p1 + q3 - c13 = 0, 0+q3 -2 = 0, q3 = 2
22 = 0, p2 + q2 – c22 = 0, p2+7 -5 = 0, p2 = -2
24 = 0, p2 + q4 – c24 = 0, -2+q4 -2 = 0, q4 = 4
34 = 0, p3 + q4 – c34 = 0, p3+ 4 -1 = 0, p3 = -3
35 = 0, p3 + q5 – c35 = 0, -3+ q5 -0 = 0, q5 = 3
Вычислим оценки свободных клеток:
21 = p2 + q1 - c21 = -2+2-1 = -1
31 = p3 + q1 - c31 = -3+2 -3 = -4
32 = p3 + q2 – c32 = -3+7-4 = 0
23 = p2 + q3 – c23 = -2+2-4 = -4
33 = p3 + q3 – c33 = -3+2-6 = -7
14 = p1 + q4 – c13 = 0+4-3 = 1
15 = p1 + q5 – c15 = 0+3 = 3
25 = p2 + q5 – c25 = -2+3 = 1
Находим наибольшую положительную оценку max (ij > 0) = 3 = 15
8
*
8-
3
5
32
28
32+
28-
37
23
25
5
25+
5-
30
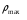 = 5
= 5
Получаем третье базисное допустимое решение:
Потребление
b1 =34
b2 =40
b3 =38
b4 =53
b5 =5
Производство
а1 =80
2
34
7
3
2
38
3
*
0
5
p1 = 0
a2 =60
1
5
37
4
2
23
0
p2 = -2
a3 =30
3
4
6
1
30
0
p3 = -3
q1 = 2
q2 = 7
q3 = 2
q4 = 4
q5 = 0
Находим новые потенциалы, новые оценки.
15 = 0, p1 + q5 – c15 = 0, 0+ q5 -0 = 0, q5 = 0
Вычислим оценки свободных клеток:
21 = p2 + q1 - c21 = -2+2-1 = -1
31 = p3 + q1 - c31 = -3+2 -3 = -4
32 = p3 + q2 – c32 = -3+7-4 = 0
23 = p2 + q3 – c23 = -2+2-4 = -4
33 = p3 + q3 – c33 = -3+2-6 = -7
14 = p1 + q4 – c14 = 0+4-3 = 1
25 = p2 + q5 – c25 = -2+0-0 = -2
35 = p3 + q5 – c15 = -3+0-0 = 0
Находим наибольшую положительную оценку max (ij > 0) = 1 = 14
3
*
3-
3
37
23
37+
23-
40
20
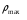 = 3
= 3
Получаем третье базисное допустимое решение:
Потребление
b1 =34
b2 =40
b3 =38
b4 =53
b5 =5
Производство
а1 =80
2
34
7
2
38
3
3
0
5
p1 = 0
a2 =60
1
5
40
4
2
20
0
p2 = -1
a3 =30
3
4
6
1
30
0
p3 = -2
q1 = 2
q2 = 6
q3 = 2
q4 = 3
q5 = 0
Находим новые потенциалы, новые оценки.
11 = 0, p1 + q1 - c11 = 0, 0+q1 -2 = 0, q1 = 2
13 = 0, p1 + q3 - c13 = 0, 0+q3 -2 = 0, q3 = 2
14 = 0, p1 + q4 - c14 = 0, 0+q4 -3 = 0, q4 = 3
24 = 0, p2 + q4 – c24 = 0, p2+3 -2 = 0, p2 = -1
22 = 0, p2 + q2 – c22 = 0, -1+q2 -5 = 0, q2 = 6
34 = 0, p3 + q4 – c34 = 0, p3+ 3 -1 = 0, p3 = -2
15 = 0, p1 + q5 – c15 = 0, 0+ q5 -0 = 0, q5 = 0
Вычислим оценки свободных клеток:
21 = p2 + q1 - c21 = -1+2-1 = 0
31 = p3 + q1 - c31 = -2+2 -3 = -3
12 = p1 + q2 – c12 = 0+6-7 = -1
32 = p3 + q2 – c32 = -2+6-4 = 0
23 = p2 + q3 – c23 = -1+2-4 = -3
33 = p3 + q3 – c33 = -2+2-6 = -6
25 = p2 + q5 – c25 = -1+0-0 = -1
35 = p1 + q5 – c15 = -2+0-0 = -2
Все ij 0
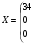
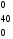
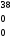
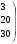
Общая стоимость всех перевозок для второго базисного допустимого решения:
L= 34*2 + 40*5 + 38*2 + 9 + 20*2+ 30 =423 – минимальная стоимость.
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. РАСПРЕДЕЛЕНИЕ КАПИТАЛЬНЫХ ВЛОЖЕНИЙ
Пусть производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций fj(xj) приведены в таблице 1, где, например, число 50 означает, что если четвёртое предприятие получит 600 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 50 тыс. руб.
Таблица 1.
xj
0 100 200 300 400 500 600 700
f 1(xj)
0 20 33 42 48 53 56 58
f 2(xj)
0 22 37 49 59 68 76 82
f 3(xj)
0 10 29 42 52 60 65 69
f 4(xj)
0 16 27 37 44 48 50 56
Прежде всего заполняем табл. 2. Значения f2(x2) складываем со значениями F1( - x2) = f1( - x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение x’2() . Заполняем таблицу 3.
Продолжая процесс, табулируем функции F3(), x’3() и т.д. В табл. 6 заполняем только одну диагональ для значения = 700.
Таблица 2
- x2 0 100 200 300 400 500 600 700
F1( - x2) 0 20 33 42 48 53 56 58
x2 f2(x2)
0 0 0 20 33 42 48 53 56 58
100 22 22* 42* 55 64 70 75 78
200 37 37 57* 70* 79 85 90
300 49 49 69 82* 91 97
400 59 59 79 92* 101*
500 68 68 88 101
600 76 76 96
700 82 82
Таблица 3
xj
0 100 200 300 400 500 600 700
F2()
0 22 42 57 70 82 92 101
x’2()
0 100 100 200 200 300 400 400
Таблица 4
- x3 0 100 200 300 400 500 600 700
F1( - x3) 0 22 42 57 70 82 92 101
x3 f3(x3)
0 0 0 22* 42* 57* 70 82 92 101
100 10 10 32 52 67 80 92 102
200 29 29 51 71* 86* 99* 111
300 42 42 64 84 99 112*
400 52 52 74 94 109
500 60 60 82 102
600 65 65 87
700 69 69
Таблица 5
xj
0 100 200 300 400 500 600 700
F3()
0 22 42 57 71 86 99 112
x’3()
0 0 0 0 200 200 200 300
Таблица 6
- x4 0 100 200 300 400 500 600 700
F1( - x4) 0 22 42 57 71 86 99 112
x4 f4(x4)
0 0 112
100 16 115*
200 27 113
300 37 108
400 44 101
500 48 90
600 50 77
700 56 56
Наибольшее число на этой диагонали: Zmax = 115 тыс. руб.,
причем четвертому предприятию должно быть выделено x*4 = x’4 (700) = 100 тыс. руб.
На долю остальных трех предприятий остается 600 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено x*3 = x’3 (700- x*4) = x’3 (600) = 200 тыс. руб.
Продолжая обратный процесс, находим x*2 = x’2 (700 - x*4 - x*3) = x’2(300) = 200 тыс. руб.
На долю первого предприятия остается x*1 = 700 - x*4 - x*3 - x*3 = 200 тыс. руб.
Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:
x*1 =200; x*2 =200; x*3 = 200; x*4 = 100.
Оно обеспечивает производственному объединению наибольший возможный прирост прибыли 115 тыс. руб.
выполнение равенства: f1(x*1) + f2(x*2) + f3(x*3) + f4(x*4) = z max
33+37+29+16=115
АНАЛИЗ ДОХОДНОСТИ И РИСКА ФИНАНСОВЫХ ОПЕРАЦИЙ
Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку и цель проведения которой заключается в максимизации дохода - разности между конечной и начальной оценками. Почти всегда финансовые операции проводятся в условиях неопределенности и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль так и убыток (или не очень большая прибыль по сравнению с той, на что надеялись проводившие эту операцию). Существует несколько разных способов оценки операции с точки зрения ее доходности и риска. Наиболее распространенным является представление дохода операции как случайной величины и оценка риска операции как среднего квадратического отклонения этого случайного дохода.
Средний ожидаемый доход: Ǭ = Σqipi
Среднее квадратическое отклонение r= 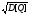
Дисперсия: D[Q] = M[Q2]- Ǭ2
Даны четыре операции Q1, Q2, Q3, Q4. Найдём средние ожидаемые доходы и риски ri операций. Нанесём точки (Ǭi, ri) на плоскость, найдём операции, оптимальные по Парето. С помощью взвешивающей формулы φ(Q)=2Q-r найдём лучшую и худшую операции.
Q1: -6 -4 -2 10
1/2 1/4 1/8 1/8
Q2: -6 -2 0 -6
1/4 1/4 1/3 1/6
Q3: -6 -5 -4 3
1/3 1/3 1/6 1/6
Q4: -6 -2 0 4
1/5 1/5 1/5 2/5
Ǭ1 = Σqipi = -6*1/2-4*1/4-2*1/8+10*1/8=-4+1=-3
D[Q1] = M[Q21]- Ǭ21
M[Q21] = 36*1/2+16*1/4+4*1/8+100*1/8=18+4+13=35
r1= 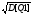 5,1
5,1
Ǭ2 = -6*1/4-2*1/4-6*1/6= -2-1= -3
M[Q22] = 36*1/4+4*1/4+36*1/6=16
r22,64
Ǭ3 = -6*1/3-5*1/3-4*1/6+3*1/6=-23/6 = -3,83
M[Q22] = 36*1/3+25*1/3+16*1/6+9*1/6=24,5
r3=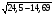 3,13
3,13
Ǭ4 = -6*1/5-2*1/5+4*2/5 = 0
M[Q22] = 36*1/5+4*1/5+16*2/5=14,4
r4 3,79
Нанесем средние ожидаемые доходы и риски r на плоскость - доход откладываем по горизонтали, а риски по вертикали (см. рис.):
Ǭ
r
0
1
2
3
4
Получили 4 точки. Чем правее точка (Ǭ, r), тем более доходная операция, чем точка выше - тем более она рисковая. Значит, нужно выбирать точку правее и ниже. Точка (Ǭ’, r') доминирует точку (Ǭ, r) если Ǭ' Ǭ и r’ r. В нашем случае 2-я операция доминирует 1-ю и 3-ю, 4-я доминирует 1-ю. Но 2-я и 4-я операции между собой не сравнимы.
Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето.
Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар (Ǭ, r) дает одно число, по которому и определяют лучшую операцию. Воспользуемся формулой φ(Q)=2Q-r . Тогда получаем:
φ(Q1)= 2*(-3)-5,1 = -11,1; φ(Q2)= 2*(-3)-2,64=-8,64; φ(Q3)= 2*(-3,83)-3,13=-10,79;
φ(Q4)= -3,79
Видно, что 4-я операция - лучшая, а 1-я - худшая.

Нравится материал? Поддержи автора!
Ещё документы из категории разное:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ
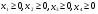 (4)
(4)