Курсовая работа

по курсу «Дискретная математика»

Тема: Разработка алгоритма и программного обеспечения для решения прикладной задачи теории графов

Вариант №22

Содержание курсовой работы

Пояснительная записка к курсовой работе должна содержать следующие разделы:

• постановка задачи;

• теоретическая часть;

• описание алгоритма решения поставленной задачи;

• ручной просчет (на небольшом примере показать работу алгоритма);

• описание программы;

• тесты;

• список использованной литературы;

• листинг программы.

ЗАДАНИЯ К КУРСОВОЙ РАБОТЕ

Некоторые базисные алгоритмы обработки графов

1. Нахождение минимального пути в графе

Путь в орграфе D из вершины v в вершину w, где v  w, называется минимальным, если он имеет минимальную длину среди всех путей орграфа D из v в w.

Назовем орграф D = (V,X) нагруженным, если на множестве дуг X определена некоторая функция l : X  R, которую часто называют весовой функцией. Значение l(x) будем называть длиной дуги x. Предположим, что l(x)  0. Длиной пути П в нагруженном орграфе будем называть величину l(П), равную сумме длин дуг, входящих в П, при этом каждая дуга учитывается столько раз, сколько она входит в данный путь.

Нагруженный орграф можно задать с помощью матрицы весов С(D) = {c_ij}_nxn с элементами

l(v_i,v_j), если (v_i,v_j) X,

c_ij =

, если (v_i,v_j) X.

ЗАДАНИЕ 1.Найти минимальные пути от фиксированной вершины до произвольной вершины графа, используя алгоритм Дейкстры.

Рассмотрим алгоритм Дейкстры, который позволяет определить минимальный путь в орграфе между двумя заданными вершинами при условии, что этот путь существует.

Пусть s – начальная вершина, t – конечная вершина. На каждой итерации любая вершина v имеет метку l^*(v), которая может быть постоянной или временной. Постоянная метка l^*(v) – это длина кратчайшего пути от s к v, временная метка l(v) – это вес кратчайшего пути из s в v, проходящий через вершины с постоянными метками. Если на каком-то шаге метка становится постоянной, то она остается такой до конца работы алгоритма.

Вторая метка (v) – это вершина, из которой вершина v получила свою метку.

А л г о р и т м Д е й к с т р ы

Данные: матрица весов С(D) орграфа D, начальная вершина s.

Результат: расстояния от вершины s до всех вершин орграфа D: D[v] = d(s,v), v  V, а также последовательность вершин, определяющая кратчайший путь из s в v .

1. Положим l^*(s) = 0 и будем считать эту метку постоянной. Для всех v V, v  s, положим l^*(v) =  и будем считать эти метки временными. Положим p = s.

2. Для всех vГp с временными метками выполним: если l^*(v)>l^*(p)+l(p,v), то l^*(v)=l^*(p)+l(p,v) и (v) =р. Иначе l^*(v) и (v) не менять, т.е. l^*(v) = min (l^*(t), l^*(p)+c_pv). (Идея состоит в следующем: пусть p – вершина, получившая постоянную метку l^*(p) на

предыдущей итерации. Просматриваем все вершины vГp, имеющие временные метки. Метка l^*(v) вершины vГp заменяется на l^*(p)+l(p,v), если оказывается, что ее метка l^*(v)>l^*(p)+l(p,v). В этом случае говорим, что вершина v получила свою метку из вершины p, поэтому положим (v) = p. С помощью этих дополнительных меток будем потом восстанавливать сам путь. Если l^*(v)  l^*(p)+c_pv, то метки остаются прежними.

3. Пусть V* - множество вершин с временными метками. Найдем вершину v* такую, что l^*(v*) = min l^*(v), v V*. Считать метку l^*(v*) постоянной для вершины v*.

4. Положим p = v*. Если p = t, то перейдем к п.5 ( l^*(t) – длина минимального пути ). Иначе перейдем к п.2.

5. Найдем минимальный путь из s в t, используя метки (v): П = s…(t)t.

Заметим, что, если продолжить работу алгоритма Дейкстры до тех пор, пока все вершины не получат постоянные метки, то мы получим расстояния от начальной вершины s до произвольной вершины графа.

ЗАДАНИЕ 2.Найти минимальные пути от фиксированной вершины до произвольной вершины графа, используя алгоритм Форда-Беллмана.

Большинство известных алгоритмов нахождения расстояния между двумя фиксированными вершинами s и t опираются на действия, которые в общих чертах можно представить следующим образом: при данной матрице весов дуг C вычисляются некоторые верхние ограничения D[v] на расстояния от s до всех вершин vV. Каждый раз, когда мы устанавливаем, что D[u] + c_uv < D[v], оценку D[v] улучшаем: D[v] = D[u] +c_uv.

Процесс прерывается, когда дальнейшее улучшение ни одного из ограничений невозможно. Можно показать, что значение каждой из переменных D[v] равно тогда d(s,v) - расстоянию от s до v. Заметим, что для того, чтобы определить расстояние от s до t, мы вычисляем здесь расстояния от s до всех вершин графа. Описанная общая схема является неполной, т.к. она не определяет очередности, в которой выбираются вершины u и v. Эта очередность оказывает сильное влияние на эффективность алгоритма. Опишем алгоритм Форда-Беллмана для нахождения расстояния от фиксированной точки s до всех остальных вершин графа.

Рассмотрим орграф D = (V,X), где V={v₁,…,v_n}.

А л г о р и т м Форда – Беллмана

Данные: матрица весов С(D) орграфа D, начальная вершина s.

Результат: расстояния от вершины s до всех вершин орграфа D: D[v] = d(s,v), v  V.

1. Всем вершинам vV орграфа присвоим метку D[v] = c_sv. Вершине s присвоим метку D[s] = 0.

2. Положим k=1.

3. Выберем произвольную вершину v V \ {s}.

4. Выберем произвольную вершину u V.

5. Положим D[v] = min (D[v], D[u] + c_uv).

6. Если вершина u пробежала еще не все множество вершин V, то выбрать среди оставшихся произвольную вершину и вернуться к шагу 5.

7. Если вершина v пробежала еще не все множество вершин V \ {s}, то выбрать среди оставшихся произвольную вершину и перейти к шагу 4.

8. Если k < n-2, то положить k=k+1 и вернуться к шагу 3, иначе алгоритм заканчивает свою работу, полученные значения D[v] будут равны расстояниям d(s,v) в орграфе D.

Замечание. Дополнить описанный алгоритм шагами, позволяющими находить сам путь от вершины s до вершины v.

Отметим, что закончить вычисления можно, когда выполнение цикла по k не вызывает изменения ни одной из переменных D[v].

Пример. Определим минимальные пути из вершины v₁ до всех остальных вершин в нагруженном орграфе D, изображенном на рис. 1.

v₄

v₁ 5 2 2 v₂

5 2

2 1 v₃

12 v₅ 2

v₆

Рис.1.

Ниже в таблице приведены матрица весов, а также все вычисления по шагам.

v₁

v₂

v₃

v₄

v₅

v₆

D⁽⁰⁾

D⁽¹⁾

D⁽²⁾

D⁽³⁾

D⁽⁴⁾

v₁





5

5

2

12

0

0

0

0

0

v₂











2



7

5

5

5

v₃



2









5

3

3

3

3

v₄



2









5

4

4

4

4

v₅





1

2





2

2

2

2

2

v₆













12

9

9

7

7

На первом шаге всем вершинам vV орграфа присвоим метку D[v] = c_sv, где s = v₁. Выберем следующую вершину v₂. Ей присвоим метку D[v₂] = min (D[v₂], D[u] + c_uv), где u V, т.е. D[v₂] = min (D[v₂], D[v₃]+ c₃₂, D[v₄]+ c₄₂, D[v₅]+ c₅₂, D[v₆]+ c₆₂) = (,5+2, 5+2, 2+, 12+) = 7. Зафиксируем, что эта метка может быть получена из вершин 3 или 4.

Аналогично корректируются метки всех оставшихся вершин, а именно,

D[v₃] = min (D[v₃], D[v₂]+c₂₃, D[v₄]+c₄₃, D[v₅]+c₅₃, D[v₆]+c₆₃) = (5,7+, 5+, 2+1, 12+) = 3,

D[v₄] = min (D[v₄], D[v₂]+c₂₄, D[v₃]+c₃₄, D[v₅]+c₅₄, D[v₆]+c₆₄) = (5,7+, 3+, 2+2, 12+) = 4,

D[v₅] = min (D[v₅], D[v₂]+ c₂₅, D[v₃]+ c₃₅, D[v₄]+ c₄₅, D[v₆]+ c₆₅) = (2,7+, 3+, 4+, 12+) = 2,

D[v₆] = min (D[v₆], D[v₂]+ c₂₆, D[v₃]+ c₃₆, D[v₄]+ c₄₆, D[v₅]+ c₅₆) = (12,7+2, 3+, 4+, 2+) = 9.

Т.к. метки вершин изменились, то продолжаем процесс дальше. Результаты третьей и четвертой итераций совпали, значит итерационный процесс можно закончить, кроме того k = n-2 = 4.

Величины, стоящие в последнем столбце, и дают длины минимальных путей из вершины v₁ до всех остальных вершин. Например, длина минимального пути из v₁ в v₂ равна 5, сам путь имеет вид: v₁v₅v₃v₂.

ЗАДАНИЕ 3.Найти минимальные пути между всеми парами вершин, используя алгоритм Флойда.

Очевидно, что задачу определения расстояния между всеми парами вершин можно решить, используя n раз (поочередно для каждой вершины) один из описанных ранее алгоритмов. Однако оказывается, что n-кратное использование этих алгоритмов не является наилучшим методом. Рассмотрим более эффективный алгоритм для решения поставленной задачи – алгоритм Флойда.

Идея этого алгоритма следующая. Рассмотрим орграф D = (V,X), где V={v₁,…,v_n}. Обозначим через d_ij^(m) длину кратчайшего из путей из v_i в v_j с промежуточными вершинами из множества {v₁,…,v_m}.

Тогда имеем следующие уравнения:

d_ij⁽⁰⁾ = c_ij,

d_ij^(m+1) = min ( d_ij^(m), d_im^(m) + d_mj^(m)).

Обоснование второго уравнения достаточно простое. Рассмотрим кратчайший путь из v_i в v_j с промежуточными вершинами из множества {v₁,…, v_m,v_m+1}. Если этот путь не содержит v_m+1 , то d_ij^(m+1) = d_ij^(m) . Если же он содержит v_m+1 , то, деля путь на отрезки от v_i до v_m+1 и от v_m+1 до v_j , получаем равенство d_ij^(m+1) = d_im^(m) + d_mj^(m) . Приведенные уравнения дают возможность вычислить расстояния d(v_i,v_j) = d_ij⁽ⁿ⁾ , где 1  i, j  n.

А л г о р и т м Ф л о й д а

Данные: матрица весов С(D) орграфа D.

Результат: расстояния между всеми парами вершин D[i,j] = d(v_i,v_j).

1. Для всех i = 1,…,n , j = 1,…,n положим D[i,j] = c_ij .

2. Для всех i = 1,…,n положим D[i,i] = 0.

3. Положим m = 1.

4. Положим i = 1.

5. Положим j = 1.

6. D[i,j] = min ( D[i,j], D[i,m] + D[m,j] ).

7. Если j < n, то положим j = j + 1 и переходим к шагу 6.

8. Если i < n, то положим i = i + 1 и переходим к шагу 5.

9. Если m < n, то положим m = m + 1 и перейдем к шагу 4, иначе алгоритм заканчивает работу. Полученные значения D[i,j] дают расстояния между вершинами v_i и v_j .

Замечание. Дополнить описанный алгоритм шагами, позволяющими находить сам путь от вершины v_i до вершины v_j.

Пример. Определим длины минимальных путей между любыми парами вершин орграфа, изображенного на рис.1. Все вычисления будем проводить с помощью матриц D.

m = 1 m = 2

v₁

v₂

v₃

v₄

v₅

v₆

v₁

v₂

v₃

v₄

v₅

v₆

v₁

0



5

5

2

12

v₁

0



5

5

2

12

v₂



0







2

v₂



0







2

v₃



2

0







v₃



2

0







v₄



2



0





v₄



2



0





v₅





1

2

0



v₅





1

2

0



v₆











0

v₆











0

Положим m = 1. Если i = 1 или j = 1, то элементы матрицы остаются без изменения, т.к. D[i,j] = min ( D[i,j], D[i,m] + D[m,j] ). Поэтому рассмотрим случай, когда i = 2 , а j = 3. Тогда D[2,3] = min ( D[2,3], D[2,1] + D[1,3] ) = min (,+5) = . Далее, j = 4, т.е. D[2,4] = min(D[2,4], D[2,1] + D[1,4] ) = min (,+5) = . Продолжаем процесс до тех пор, пока i  6 и j  6. Положим m = 2 и продолжим рассуждения дальше.

m = 3 m = 4

v₁

v₂

v₃

v₄

v₅

v₆

v₁

v₂

v₃

v₄

v₅

v₆

v₁

0



5

5

2

12

v₁

0

7

5

5

2

9

v₂



0







2

v₂



0







2

v₃



2

0





4

v₃



2

0





4

v₄



2



0



4

v₄



2



0



4

v₅





1

2

0



v₅



3

1

2

0

5

v₆











0

v₆











0

m = 5 m = 6

v₁

v₂

v₃

v₄

v₅

v₆

v₁

v₂

v₃

v₄

v₅

v₆

v₁

0

7

5

5

2

9

v₁

0

5

3

4

2

7

v₂



0







2

v₂



0







2

v₃



2

0





4

v₃



2

0





4

v₄



2



0



4

v₄



2



0



4

v₅



3

1

2

0

5

v₅



3

1

2

0

5

v₆











0

v₆











0

Матрица D:

v₁

v₂

v₃

v₄

v₅

v₆

v₁

0

5

3

4

2

7

v₂



0







2

v₃



2

0





4

v₄



2



0



4

v₅



3

1

2

0

5

v₆











0

2. Эйлеровы цепи и циклы

Пусть G – псевдограф. Цепь (цикл) в G называется эйлеровой (эйлеровым), если она (он) проходит по одному разу через каждое ребро псевдографа G.

Для того, чтобы связный псевдограф G обладал эйлеровым циклом, необходимо и достаточно, чтобы степени его вершин были четными.

Для того, чтобы связный псевдограф G обладал эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно две вершины нечетной степени. Если указанное условие выполняется, то любая эйлерова цепь псевдографа G соединяет вершины нечетной степени.

Пусть G – связный мультиграф, степени вершин которого – четные числа.

ЗАДАНИЕ 4.Построить эйлеров цикл в графе.

А л г о р и т м построения эйлерова цикла

Данные: матрица инцидентности В(G) мультиграфа G.

Результат: последовательность ребер, образующих эйлеров цикл.

1. Выбрать произвольную вершину v.

2. Выбрать произвольное ребро x, инцидентное v, и присвоить ему номер 1. (Назовем это ребро “пройденным”).

3. Каждое пройденное ребро вычеркивать и присваивать ему номер, на единицу больший номера предыдущего вычеркнутого ребра.

4. Находясь в вершине w, не выбирать ребра, соединяющего w с v, если только есть возможность другого выбора.

5. Находясь в вершине w, не выбирать ребра, которое является “перешейком” (при удалении которого граф, образованный незачеркнутыми ребрами, распадается на две компоненты связности, имеющие хотя бы по одному ребру).

6. После того, как в графе будут занумерованы все ребра, цикл  = [x_i1, x_i2,…, x_im], образованный ребрами с номерами от 1 до m, где m – число ребер в графе, есть эйлеров цикл.

Замечание. Прежде чем строить эйлеров цикл, проверить условие существования этого цикла.

ЗАДАНИЕ 5.Построить эйлерову цепь в графе.

Изменить алгоритм построения эйлерова цикла так, чтобы можно было использовать его для построения эйлеровой цепи в графе.

3. Гамильтоновы цепи и циклы

Пусть G – псевдограф. Цепь (цикл) в G называется гамильтоновой (гамильтоновым), если она (он) проходит через каждую вершину псевдографа G ровно один раз. Простейшим достаточным условием существования гамильтоновых цепей и циклов в графе является его полнота. Граф G называется полным, если каждая его вершина смежна со всеми остальными вершинами. Необходимым условием существования гамильтоновых цепей и циклов в графе G является связность данного графа.

Приведем некоторые наиболее простые методы выделения гамильтоновых цепей и циклов в графе G =(V,X), где V = {v₁ ,v₂ ,…,v_n}. Самым простым является метод перебора всевозможных перестановок v_i1 ,v_i2 ,…,v_in множества V. Для каждой из них проверяем, является ли v_i1v_i2…v_in маршрутом в G. Если является, то v_i1v_i2 …v_in - гамильтонова цепь в G, в противном случае переходим к другой перестановке. Тогда по окончании перебора будут выделены все гамильтоновы цепи в графе G. Аналогично для выделения гамильтоновых циклов перебираем всевозможные перестановки v₁v_i1v_i2 …v_in-1 множества V, для каждой из которых проверяем, является ли v₁v_i1v_i2…v_in-1v₁ маршрутом в G. Если является, то v₁v_i1v_i2…v_in-1v₁ – гамильтонов цикл в G, в противном случае переходим к следующей перестановке. Тогда по окончании перебора будут выделены все гамильтоновы циклы в графе G. Очевидно, что при выделении гамильтоновых цепей придется перебрать n! перестановок, а при выделении всех гамильтоновых циклов - (n-1)! перестановок. При этом в случае полного графа ни одна из перестановок не окажется отброшенной, т.е. данный метод является эффективным для графов, близких к полным.

Отметим, что описанный метод не учитывает информации об исследуемом графе G и является как бы ориентированным на самый “худший” случай, когда G – полный граф.

Для того, чтобы сократить число шагов в предложенном методе, рассмотрим следующий алгоритм. Предположим, что решение имеет вид последовательности <v₁, ... v_n>. Идея метода состоит в следующем: решение строится последовательно, начиная с пустой последовательности (длины 0). Далее, имея частичное решение <v₁, ... v_i>, ищем такое допустимое значение v_i+1, которое еще не было использовано, добавляем его к пройденному частичному решению и продолжаем процесс для нового частичного решения <v₁, ... v_i+1>. В противном случае, если такого значения v_i+1 не существует, возвращаемся к предыдущему частичному решению <v₁, ... v_i-1> и продолжаем процесс, пытаясь определить новое, еще не использованное допустимое значение v_k. Такие алгоритмы носят название “алгоритмы с возвратом” (англ.: backtracking).

2 1

1 5 3 12 14

4

123 125 143 145

1234 1235 1253 1254 1432 1435 1452 1453

14321 14352

12341 12354 12534

14325 14521 14532

12345 12541 12543 14523

123541 125341 143521 145321

Рис. 2

Процесс поиска с возвращением удобно проиллюстрировать в терминах обхода в глубину в некотором дереве поиска, которое строится следующим образом. Каждая вершина дерева соответствует некоторому частичному решению <v₁,...v_i>, причем вершины, соответствующие последовательностям вида <v₁,.. v_i, y>, и являются преемниками вершины <v₁,... v_i>. Корнем данного дерева является пустая последовательность. В случае построения гамильтонова цикла в качестве корня может выступать любая вершина.

При обходе дерева в глубину вершины дерева посещаются в таком порядке: сначала посещаем корень дерева v₁, а затем (если v₁ – не висячая вершина) для каждого преемника v_i корня v₁ рекурсивно обращаемся к процедуре обхода в глубину для того, чтобы обойти все поддеревья с корнями v_i в порядке, в котором упорядочены вершины v_i как преемники корня v₁.

Пример.

На рис.2 показаны граф и дерево, иллюстрирующее процесс нахождения всех гамильтоновых циклов с помощью алгоритма с возвратом.

Гамильтоновы циклы – 123541, 125341, 143521, 145321.

1. Генерирование всех перестановок заданного множества

Напомним, что перестановкой n-элементного множества X называется упорядоченный набор длины n, составленный из попарно различных элементов множества X. Опишем некоторые методы генерирования последовательности всех n перестановок n-элементного множества. Не нарушая общности будем рассматривать не исходное множество Х, а множество А={1,2,…n} – множество индексов элементов, т.к. между множеством элементов из Х и множеством индексов из А существует взаимно однозначное соответствие, которое задается в виде: x_i  i.

Будем предполагать, что элементы множества запоминаются в виде элементов массива Р1,…, Рn. Во всех методах элементарной операцией, которая применяется к массиву Р, является поэлементная транспозиция, т.е. обмен значениями переменных Рi и Рj, где 1i, jn. Эту операцию будем обозначать Рi :=: Рj. Очевидно, что она эквивалентна последовательности команд: а := Рi  Рi := Рj Рj := а, где а – некоторая вспомогательная переменная.

Генерирование всех перестановок заданного множества в лексикографическом порядке

Данный метод легче всего понять, если в качестве переставляемых элементов взять числа 1,…,n. На множестве всех перестановок определим лексикографический порядок:

x₁,x₂,…x_n < y₁,y₂,…,y_n  существует k1, такое что xk < yk и xp= yp для каждого p < k.

Заметим, что если вместо чисел 1,2,…, n взять буквы а,б,…,р с естественным порядком абв…р, то лексикографический порядок определяет стандартную последовательность, в которой слова длины n появляются в словаре.

Для примера приведем перестановки множества X = {1,2,3} в лексикографическом порядке:

123, 132, 213, 231, 312, 321.

Начиная с перестановки (1,2,…,n), переход от текущей перестановки P=(p₁,p₂,…,p_n) к перестановке, следующей за текущей в смысле лексикографического порядка, осуществляется последовательным выполнением следующих действий:

2)просмотр Р справа налево в поисках самой правой позиции k, в которой p_k<p_k+1 (если такой позиции k нет, то текущая перестановка является последней и следует закончить генерацию);

3)просмотр P от p_k слева направо в поисках наименьшего из таких элементов p_m, что k<m и p_k<p_m; транспозиция элементов p_k и p_m и обращение отрезка p_k+1,…, p_n путем транспозиции симметрично расположенных элементов (заметим, что элементы обращаемого отрезка расположены в порядке убывания).

Например, для п=8 и Р=(2,6,5,8,7,4,3,1) имеем p_k =5 и p_m=7, результат транспозиции p_k и p_m - (2,6,7,8,5,4,3,1), результат обращения отрезка p_k+1,…, p_n переводит Р в перестановку (2,6,7,1,3,4,5,8), которая следует за Р в лексикографическом порядке.

Рекурсивный алгоритм генерирования всех перестановок заданного множества в лексикографическом порядке

Рассмотрим рекурсивный алгоритм генерирования перестановок в лексикографическом порядке. Заметим, что последовательность перестановок множества {1,2,…, n} в этом случае имеет следующие свойства, вытекающие непосредственно из определения:

1. в первой перестановке элементы идут в растущей последовательности, а в последней – в убывающей другими словами последняя перестановка является обращением первой,

2. последовательность всех перестановок можно разделить на n блоков длины (n-1), соответствующих возрастающим значениям элемента в первой позиции. Последние n-1 позиций блока, содержащего элемент р в первой позиции, определяют последовательность перестановок множества {1,2,…, n}\{р} в лексикографическом порядке.

В качестве примера рассмотрим генерирование всех перестановок для п=4. Таких перестановок будет 4!=24. Эти перестановки можно разбить на четыре блока, каждый из которых содержит 3!=6 перестановок, по значению элемента в первой позиции. В первом блоке на первом месте стоит 1, во втором – 2, в третьем – 3, в четвертом – 4. Далее рассмотрим блок с 1 на первом месте, для остальных аналогично. Для генерации всех перестановок оставшегося множества Х={2,3,4} выполним следующее: разобъем все перестановки на 3 блока по 2!=2 перестановки, соответствующих возрастающим значениям элемента в первой позиции, в первом блоке – 2, во втором – 3, в третьем – 4. Далее в каждом блоке генерируем все перестановки из оставшихся двух элементов в лексикографическом порядке (в первой из перестановок последние два элемента расположены в порядке возрастания). В результате получаем:

1

2

3

4

2

1

3

4

3

1

2

4

4

1

2

3

1

2

4

3

2

1

4

3

3

1

4

2

4

1

3

2

1

3

2

4

2

3

1

4

3

2

1

4

4

2

1

3

1

3

4

2

2

3

4

1

3

2

4

1

4

2

3

1

1

4

2

3

2

4

1

3

3

4

1

2

4

3

1

2

1

4

3

2

2

4

3

1

3

4

2

1

4

3

2

1

Генерирование всех перестановок заданного множества в антилексикографическом порядке

Антилексикографический порядок (обозначим  ) определяется следующим образом:

x1,x2,…xn < y1,y2,…,y n  существует такое kn, что xk  yk и xp = yp для каждого p  k..

Для примера приведем перестановки множества X = {1,2,3} в антилексикографическом порядке: 123, 213, 132, 312, 231, 321.

Алгоритм генерирования перестановок в антилексикографическом порядке сформулировать удобнее. Заметим, что последовательность перестановок множества {1,2,…, n} в этом случае имеет следующие свойства, вытекающие непосредственно из определения:

1. в первой перестановке элементы идут в растущей последовательности, в последней – в убывающей другими словами, последняя перестановка – обращение первой,

4)последовательность всех перестановок можно разделить на n блоков длины (n-1), соответствующих убывающим значениям элемента в последней позиции. Первые n-1 позиций блока, содержащего элемент р в последней позиции, определяют последовательность перестановок множества {1,2,…, n}\{р} в антилексикографическом порядке.

Сгенерируем в антилексикографическом порядке все перестановки для n=4, получим

1

2

3

4

1

2

4

3

1

3

4

2

2

3

4

1

2

1

3

4

2

1

4

3

3

1

4

2

3

2

4

1

1

3

2

4

1

4

2

3

1

4

3

2

4

2

3

1

3

1

2

4

4

1

2

3

4

1

3

2

2

4

3

1

2

3

1

4

2

4

1

3

3

4

1

2

3

4

2

1

3

2

1

4

4

2

1

3

4

3

1

2

4

3

2

1

ЗАДАНИЕ 1.Построить гамильтонов цикл в графе, используя нерекурсивный алгоритм генерации всех перестановок вершин в лексикографическом порядке

ЗАДАНИЕ 2.Построить гамильтонов цикл в графе, используя рекурсивный алгоритм генерации всех перестановок вершин в лексикографическом порядке

ЗАДАНИЕ 3.Построить гамильтонов цикл в графе, используя рекурсивный алгоритм генерации всех перестановок вершин в антилексикографическом порядке.

ЗАДАНИЕ 4.Построить гамильтонову цепь в графе, используя нерекурсивный алгоритм генерации всех перестановок вершин в лексикографическом порядке

ЗАДАНИЕ 5.Построить гамильтонову цепь в графе, используя рекурсивный алгоритм генерации всех перестановок вершин в лексикографическом порядке

ЗАДАНИЕ 6.Построить гамильтонову цепь в графе, используя рекурсивный алгоритм генерации всех перестановок вершин в антилексикографическом порядке.

ЗАДАНИЕ 7.Построить гамильтонов цикл в графе, используя алгоритм с возвратом.

ЗАДАНИЕ 8.Построить гамильтонову цепь в графе, используя алгоритм с возвратом.

4. Построение остова минимального веса

Граф G называется деревом, если он является связным и не имеет циклов.

Остовом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Остовное дерево связного нагруженного графа G с минимальной суммой длин содержащихся в нем ребер, будем называть остовом минимального веса или минимальным остовным деревом (МОД).

Рассмотрим граф G = (V,X), где V={v₁,…,v_n}.

ЗАДАНИЕ 9.Найти минимальный остов графа, используя алгоритм Краскала.

А л г о р и т м К р а с к а л а

Данные: матрица весов С(G) графа G.

Результат: матрица весов полученного остова, величина минимального остова.

1. Выберем в графе G ребро х минимального веса и построим граф G₁, присоединяя к пустому графу О_n на множестве вершин V ребро х.

2. Если граф G_к уже построен и k < n-1, то строим граф G_к+1, присоединяя к графу G_к ребро y, имеющее минимальный вес среди ребер, не входящих в G_к и не составляющих циклов с ребрами из G_к.

В качестве иллюстрации рассмотрим нагруженный граф, изображенный на рис. 3а). На рис. 3б) представлено МОД данного графа (в скобках указан порядок присоединения ребер к МОД). Длина полученного МОД равна 10.

1 3 5 1 5

1 2 4 4 (1) (2) (4)

(3)

4 5 2 3 3 4 2 3

а) б)

Рис. 3

ЗАДАНИЕ 10.Найти минимальный остов графа, используя алгоритм Прима.

Алгоритм Прима отличается от алгоритма Краскала только тем, что на каждом этапе строится не просто ациклический граф, а дерево.

А л г о р и т м П р и м а

Данные: матрица весов С(G) графа G.

Результат: матрица весов полученного остова, величина минимального остова.

1. Выберем в графе G ребро х = v,w минимального веса и построим дерево G₁ = (V₁,X₁), полагая V₁ = {v,w}, X₁ = {х}.

2. Если дерево G_к уже построено и k < n-1, то среди ребер, соединяющих вершины этого дерева с вершинами графа G, не входящими в G_к , выбираем ребро y минимального веса. Строим дерево G_к+1, присоединяя к G_к ребро y вместе с его не входящим в G_к концом.

5. Поиск в графах

Существует много алгоритмов на графах, в основе которых лежит систематический перебор вершин графа, такой, что каждая вершина графа просматривается только один раз, и переход от одной вершины к другой осуществляется по ребрам графа. Остановимся на двух стандартных методах такого перебора: поиск в глубину и поиск в ширину.

Рассмотрим метод поиска в глубину в неориентированном графе G. Идея этого метода состоит в следующем. Начинаем поиск с некоторой фиксированной вершины v₀, присвоим ей ПГ-номер: ПГ(v₀)=1. Затем выбираем произвольную вершину w, смежную с v₀, присваиваем ей ПГ-номер: ПГ(w)=2, и повторяем процесс уже от вершины w. Предположим, что в результате выполнения нескольких шагов этого процесса мы пришли в вершину v и пусть ПГ(v)=k. Далее действуем в зависимости от ситуации следующим образом:

1. если имеется новая, т.е. еще непросмотренная вершина u, смежная с v, то, присваивая ей ПГ-номер: ПГ(u)=k+1, продолжаем поиск, начиная с вершины u;

5) если же не существует ни одной новой, т.е. непросмотренной вершины u, смежной с v, то считаем, что вершина v просмотрена и возвращаемся в вершину, из которой мы попали в v, и продолжаем процесс поиска дальше.

Пример.

7 1 8

5 6 2 5

9

1 3 8

3 6

7 10

2 9 10

4 4

а) б)

Рис. 4

Поиск в глубину завершается, когда все вершины графа просмотрены. Если в результате работы алгоритма произошел возврат в начальную вершину v₀, но при этом не все вершины графа просмотрены, то необходимо выбрать произвольную вершину из непросмотренных и продолжить процесс поиска от этой вершины. В результате проведенного поиска пройденные ребра графа образуют вместе с пройденными вершинами одно или несколько деревьев. Если приписать пройденным ребрам ориентацию в соответствии с тем направлением, в каком они проходятся при выполнении поиска, то получится совокупность корневых деревьев, корнями которых служат начальные вершины.

Для графа, представленного на рис. 4 а), описанным методом были получены два корневых дерева, изображенных на рис 4б).

Рассмотрим идею поиска в ширину в неориентированном графе. Другое название этого метода – волновой.

Начинается поиск с произвольной вершины v. Ей приписывается номер 0. Вершину v считаем просмотренной и помещаем в очередь. Далее проходим все ребра {v, w}, инцидентные вершине v и ориентируем их из v в w. Всем вершинам w приписываем номер 1, считаем их просмотренными и помещаем в очередь. После этих действий вершина v удаляется из очереди.

Далее выбираем вершину u, которая находится в начале очереди. Пусть ей приписан номер k. Пройдем все ребра, соединяющие вершину u с еще непросмотренными вершинами w. Всем вершинам w присвоим номер k+1, будем считать их просмотренными и поместим в очередь в порядке их просмотра. После этого вершину u удаляем из очереди. Заканчивается поиск в ширину тогда, когда все вершины графа будут просмотрены.

Пример.

7(2)

5(1) 6(2)

1(0) 3(1)

2(1) 4(1)

Рис. 5

На рис 5 в скобках указаны номера вершин графа, которые были ими получены в результате поиска в ширину.

Рассмотренная методика поиска в глубину и в ширину переносится и на ориентированные графы.

Рассмотренные методы поиска в глубину и в ширину могут быть применены для нахождения путей (маршрутов) в орграфах (графах), для выделения компонент связности (компонент сильной связности) графа (орграфа), а также для решения других задач теории графов.

ЗАДАНИЕ 1.Выделить компоненты сильной связности орграфа, используя алгоритм поиска в глубину (в орграфе поиск необходимо вести как в прямом, так и в обратном направлении).

ЗАДАНИЕ 2.Выделить компоненты сильной связности орграфа, используя алгоритм поиска в ширину (в орграфе поиск необходимо вести как в прямом, так и в обратном направлении).

Независимые множества вершин и родственные задачи

1. Независимые множества

Во многих прикладных задачах требуется найти в конечном множестве объектов максимальную систему объектов, попарно не связанных друг с другом, или же выбрать минимальную систему объектов, связанных со всеми другими. Формулировки подобных задач на языке теории графов приводят к понятиям независимости и покрытия.

Множество вершин U графа G = (V,X) называется независимым (внутренне устойчивым), если никакие две вершины из этого множества не смежны. Другими словами, если U V и U независимо в графе G, то порожденный подграф G(U) является пустым. Очевидно, что если при этом U* U, то U* - также независимое множество.

Внутренне устойчивое множество называется максимальным, если оно не является собственным подмножеством некоторого другого независимого множества.

Наибольшее по мощности независимое множество называется наибольшим.

Ясно, что наибольшее независимое множество является максимальным. Обратное, вообще говоря, неверно.

Число вершин в наибольшем независимом множестве графа G называется числом независимости (или числом внутренней устойчивости) этого графа и обозначается (G).

2

1 3 7

5 4 6

8

Рис. 1.

Например, для графа G, изображенного на рис.1., (G)=4, множества вершин {1,2,3,7}, {1,2,3,8}, {2,3,5,7}, {2,3,5,8} являются наибольшими независимыми, а {4,7} – максимальное независимое множество, не являющееся наибольшим.

Понятие внутренней устойчивости естественным образом переносятся и на случай ориентированного графа.

Алгоритм с возвратом

Очевидный алгоритм, который можно применить для нахождения независимых множеств вершин, это «полный перебор всех возможностей»: генерируем все возможные подмножества вершин заданного графа или орграфа и проверяем, является ли оно независимым. Среди всех независимых множеств выбираем максимальные. Опишем теперь общий метод, позволяющий значительно сократить число шагов в алгоритмах полного перебора всех возможностей. Чтобы применить этот метод, представим искомое решение в виде последовательности <x₁,…x _n>. Основная идея метода состоит в том, что решение строится последовательно, начиная с пустой последовательности ε (длины 0). Вообще, имея данное частичное решение <x₁,…x _k>, мы стараемся найти такое допустимое значение x _k+1, относительно которого мы не можем сразу сказать, что <x₁,…x _k, x _k+1> можно расширить до некоторого решения (либо <x₁,…x _k, x _k+1> уже является решением). Если такое предполагаемое, но еще не использованное значение x _k+1 существует, то мы добавляем его к нашему частичному решению и продолжаем процесс для последовательности <x₁,…x _k, x _k+1>. Если его не существует, то мы возвращаемся к нашему частичному решению <x₁,…x _k-1> и продолжаем процесс, отыскивая новое, еще не использованное допустимое значение x_k – отсюда название «алгоритм с возвратом» (англ.: backtracking).

b.Раскраска графа

Задачи раскраски вершин или ребер графа занимают важное место в теории графов. К построению раскрасок сводится целый ряд практических задач. Характерной особенностью этих задач является существование объектов, которые по каким-либо причинам не могут быть объединены в одну группу.

Пусть G – некоторый граф, k – натуральное число. Произвольная функция вида f: V → {1,2,…,k} называется вершинной k-раскраской или просто k-раскраской графа G.

Раскраска называется правильной, если f(v)≠f(u) для любых смежных вершин v и u. Граф, для которого существует правильная k-раскраска, называется k-раскрашиваемым.

Минимальное число k, при котором граф G является k-раскрашиваемым, называется хроматическим числом этого графа и обозначается χ (G). Если χ (G)=k, то граф называется k-хроматическим. Правильная k-раскраска графа при k =χ (G) называется минимальной.

Алгоритм раскрашивания графов

1. Выберем в графе G некоторое максимальное независимое множество вершин U (лучше наибольшее). Покрасим все вершины данного множества в один цвет.

2. Выберем максимальное независимое множество вершин U₁ в графе G₁, который получается из графа G удалением множества вершин U и всех инцидентных им ребер. Покрасим вершины множества U₁ в очередной цвет.

3. Шаг 2 повторять до тех пор, пока в графе G не будут раскрашены все вершины.

Реберной k-раскраской графа G называется функция φ, ставящая в соответствие каждому его ребру x число φ(x) из множества {1,2,…,k}. Реберная окраска называется правильной, если смежные ребра имеют разные цвета. Граф, допускающий правильную реберную k-раскраску, называется реберно k-раскрашиваемым. Минимальное число k, при котором граф G является реберно k-раскрашиваемым, называется хроматическим классом (хроматическим индексом или реберным хроматическим числом) графа G и обозначается через χ ‘(G). Если χ ‘(G)=k, то граф называется реберно k-хроматическим.

Независимые множества ребер графа G находятся во взаимно однозначном соответствии с независимыми множествами вершин реберного графа L(G)=(V₁,X₁), который для графа G=(V,X) определяется следующими двумя условиями:

1. V₁ = X,

2. вершины х₁ и х₂ смежны в L(G) тогда и только тогда, когда ребра х₁ и х₂ смежны в G.

На рис. 2 изображены два графа – G и L(G). Вершины графа G – темные кружки, вершины графа L(G) – светлые кружки. Ребра графа G – тонкие линии, ребра графа L(G) – жирные линии.

Рис. 2

Поскольку ребра любого графа G смежны тогда, когда смежны соответствующие вершины реберного графа L(G) (правило построения реберного графа смотри ниже), то χ ‘(G) можно определить как хроматическое число графа L(G), т.е. χ ‘(G)=χ (L(G)).

ЗАДАНИЕ 1.Найти хроматическое число заданного графа, используя алгоритм с возвратом для нахождения независимых множеств вершин, указать, какие вершины в какой цвет окрашиваются.

ЗАДАНИЕ 2.Найти хроматический класс заданного графа, используя алгоритм с возвратом для нахождения независимых множеств вершин реберного графа, указать, какие ребра в какой цвет окрашиваются.

c.Паросочетания

Не менее важным, чем понятие вершинной независимости, является понятие реберной независимости.

Произвольное подмножество попарно несмежных ребер графа называется паросочетанием ( или независимым множеством ребер).

В качестве иллюстрации рассмотрим граф, изображенный на рис.2. В нем паросочетаниями являются, например, х₁,х₃,х₅,х₇, х₁, х₂, х₂,х₆.

х₁ х₂ х₃ х₄ х₅ х₆ х₇

Рис. 3.

Паросочетание графа G называется максимальным, если оно не содержится в паросочетании с большим числом ребер, и наибольшим, если число ребер в нем наибольшее среди всех паросочетаний графа G.

Число ребер в наибольшем паросочетании графа G называется числом паросочетания и обозначается ₁(G).

Независимые множества ребер графа G находятся во взаимно однозначном соответствии с независимыми множествами вершин реберного графа L(G)=(V₁,X₁), который для графа G=(V,X) определяется следующими двумя условиями:

1. V₁ = X,

2. вершины х₁ и х₂ смежны в L(G) тогда и только тогда, когда ребра х₁ и х₂ смежны в G.

Рис. 4

На рис. 4 изображены два графа – G и L(G). Вершины графа G – темные кружки, вершины графа L(G) – светлые кружки. Ребра графа G – тонкие линии, ребра графа L(G) – жирные линии.

ЗАДАНИЕ 1.Найти все максимальные паросочетания в заданном графе, используя алгоритм с возвратом для нахождения независимых множеств вершин реберного графа.

ЗАДАНИЕ 2.Найти наибольшее паросочетание в заданном графе, используя алгоритм с возвратом для нахождения независимых множеств вершин реберного графа.

Потоки в сетях и родственные задачи

1. Потоки в сетях

1. Полный поток в транспортной сети

Теория транспортных сетей возникла при решении задач, связанных с организацией перевозки грузов. Тем не менее понятие потока на транспортной сети, алгоритм нахождения потока наибольшей величины и критерий существования потока, насыщающего выходные дуги сети, оказались полезными для многих других прикладных и теоретических вопросов комбинаторного характера.

Введем основные понятия данной теории.

Транспортной сетью называется орграф D = (V,X) с множеством вершин V = {v₁,…,v_n}, для которого выполняются условия:

1. существует одна и только одна вершина v₁, называемая источником, такая, что Г^-1 (v₁) =  (т.е. ни одна дуга не заходит в v₁),

6)существует одна и только одна вершина v_n, называемая стоком, такая, что Г(v_n) =  (т.е. из v_n не исходит ни одной дуги),

7)каждой дуге xX поставлено в соответствие целое число c (x)  0, называемое пропускной способностью дуги.

Функция (x), определенная на множестве X дуг транспортной сети D и принимающая целочисленные значения, называется допустимым потоком (или просто потоком) в транспортной сети D, если

1. для любой дуги xX величина (x), называемая потоком по дуге x, удовлетворяет условию 0  (x)  c(x),

8)для любой промежуточной вершины v сумма потоков по дугам, заходящим в v, равна сумме потоков по дугам, исходящим из v.

Величиной потока  в транспортной сети D называется величина, равная сумме потоков по всем дугам, заходящим в сток, или, что то же самое сумме потоков по всем дугам, исходящим из источника.

Дуга xX называется насыщенной, если поток по ней равен ее пропускной способности. Поток  называется полным, если любой путь в сети из источника в сток содержит, по крайней мере, одну насыщенную дугу.

А л г о р и т м

построения полного потока в сети

Данные: транспортная сеть D, заданная матрицей пропускных способностей дуг.

Результат: полный поток в сети.

1. Полагаем для любой дуги xХ (x) = 0 ( начинаем с нулевого потока ).

2. Полагаем D* = D.

3. Удаляем из орграфа D* все дуги, являющиеся насыщенными при потоке  в транспортной сети D. Полученный орграф снова обозначим через D*.

4. Ищем в D* простую цепь  из v₁ в v_n . Если такой цепи нет, то  - искомый полный поток в транспортной сети D. В противном случае переходим к шагу 5.

5. Увеличиваем поток (x) по каждой дуге x из  на одинаковую величину a>0 такую, что, по крайней мере, одна дуга из  окажется насыщенной, а потоки по всем остальным дугам из  не превышают их пропускных способностей. При этом величина потока  также увеличится на a, а сам поток  в транспортной сети D остается допустимым. После этого перейдем к шагу 3.

ЗАДАНИЕ 1.Максимальный поток

Поток  называется максимальным, если его величина принимает максимальное значение по сравнению с другими допустимыми потоками в транспортной сети D. Максимальный поток всегда является полным (обратное, вообще говоря, неверно).

Введем для заданной транспортной сети D и допустимого потока  в этой сети орграф приращений I(D,), имеющий те же вершины, что и сеть D. Каждой дуге x = (v,w)  X транспортной сети D в орграфе приращений I(D, ) соответствуют две дуги: x и x* = (w,v) – дуга, противоположная по направлению дуге x. Припишем дугам x и x* орграфа приращений I(D, ) длину l:

0, если (x) < c(x),

l(x) =

, если (x) = c(x),

0, если (x) > 0,

l(x*) =

, если (x) = 0.

А л г о р и т м

построения максимального потока

Данные: транспортная сеть D, заданная матрицей пропускных способностей дуг.

Результат: максимальный поток в сети.

1. Полагаем i = 0. Пусть ₀ – любой допустимый поток в транспортной сети D (например, полный или нулевой).

2. По сети D и потоку _i строим орграф приращений I(D, _i).

3. Находим простую цепь _i, являющуюся минимальным путем из v₁ в v_n в нагруженном орграфе I(D, _i) (можно использовать любой описанный выше алгоритм). Если длина этой цепи равна , то поток _i максимален и работа алгоритма заканчивается. В противном случае увеличиваем поток вдоль цепи _i на максимально допустимую величину a_i > 0, где a_iZ (прибавляя ее для каждой дуги xX, через которую проходит цепь _i, к уже имеющейся величине потока по дуге x, если дуга x входит в _i, и вычитая, если дуга x* входит в _i), такую, что при этом сохраняется условие допустимого потока. В результате меняется поток в транспортной сети D, т.е. от потока _i переходим к потоку _i+1, который является допустимым, и при этом величина его увеличивается на a_i. Присваиваем i = i + 1 и переходим к шагу 2.

Алгоритм меток для нахождения максимального потока

Рассмотрим другой алгоритм построения максимального потока в транспортной сети, использующий метки вершин.

Помечивающий алгоритм Форда – Фалкерсона

для нахождения максимального потока

Данные: транспортная сеть D, заданная матрицей пропускных способностей дуг.

Результат: максимальный поток в сети.

1. Построить произвольный поток φ на транспортной сети D (например, положить φ(u) = 0 для любой дуги u ).

2. Просмотреть пути, соединяющие вход сети v₁ с выходом v_n. Если поток φ полный, то перейти к п.4.

3. В противном случае рассмотреть путь μ, соединяющий вход сети v₁ с выходом v_n, все дуги которого не насыщены. Построить новый поток φ´:

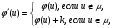
где 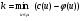. Повторить этот процесс до получения

полного потока φ.

9)Присвоить целочисленные метки вершинам сети D и знаки «+» или «-» дугам по правилам:

• входу v₁ присвоить метку 0,

• если вершина v_i получила некоторую метку, а y - еще непомеченная вершина, то вершине yГv_i, такой что φ((v_i,y))<c((v_i,y)) присвоить метку i, а дуге (v_i,y) – знак «+»; вершине y Г^-1v_i , такой, что φ((y,v_i))>0, присвоить метку i, а дуге (y,v_i) – «-». Остальные непомеченные вершины и дуги метки и знаки не получают;

• повторять процесс, описанный в предыдущем пункте до тех пор, пока не прекратится появление новых отмеченных вершин и дуг. Если в результате выполнения этого пункта вершина v_n не получит метки, то поток является максимальным. В противном случае перейти к п.5.

10)Рассмотреть последовательность отмеченных вершин λ=(v_n, v_i1, v_i2,…,v₁), каждая из которых имеет метку, равную номеру последующей вершины, и последовательность μ (не обязательно путь), соединяющих последовательные вершины из λ. Построить новый поток φ´:

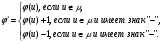
Перейти к пункту 4.

Пример. Рассмотрим транспортную сеть D и полный поток φ, для которого 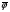= 14:

2. (1,+)

7(8) 7(7)

0 (1,+) 5 (3,-) 6 (4,+)

1 4(5) 3 6(7) 1(1)

3(3) 10(10) 0(3) 13(15)

4 (5,+) Рис. 1.

Присвоим вершине 1 метку 0, тогда вершине 2 присвоим метку (1,+), т.к. φ((1,2))Т.к. φ((2,5))=c((2,5)), то переходим к вершине 3, которой присвоим метку (1,+), затем вершине 5 – (3,-), вершине 4 – (5,+), вершине 6 – метку (4,+). Рассмотрим последовательность вершин λ=(6,4,5,2,1), и построим новый поток, величина которого равна 15.

2. (1,+)

7(8) 7(7)

0 5 6

1 5 (5) 3 5(7) 1(1)

3(3) 10(10) 1(3) 14(15)

4. Рис. 2.

Нетрудно заметить, что улучшить данный поток нельзя.

a.Некоторые прикладные задачи

1. Задачи об источниках и потребителях

В задачах этого типа встречаются три рода объектов: «источники», «потребители», «промежуточные пункты». Источниками могут быть электростанции, заводы, контрольно-измерительные приборы, железнолорожные станции и т.д., которые поставляют соответственно электроэнергию, изделия, информацию, грузы и т.д. для потребителей. В промежуточных пунктах может происходить, например, преобразование электроэнергии, упаковка или комплектация изделий, кодирование информации, перевалка грузов, причем, что весьма существенно, без изменения количества грузов. Источники, промежуточные пункты и потребители связаны сетью линий передач или автомобильными, железнодорожными, морскими линиями или каналами связи с заданными пропускными способностями.

Пусть в некоторую единицу времени источники x_j (j=1,2,..,k) вырабатывают a_j единиц продукции, а потребность потребителя y_i (I=1,2,..,m) в этой продукции равна b_i. Пропускные способности линий считаются также отнесенными к выбранной единице времени. Таким образом, в задачах этого типа идет речь о неизменном и однородном по времени стационарном потоке.

С каждой такой задачей свяжем транспортную сеть D. Вершинами сети D служат источники, потребители, промежуточные пункты и еще две вспомогательные вершины: вход x₀ и выход z. Вершину x₀ свяжем дугами (x₀,x_j) (j=1,..,k) с источниками и припишем им пропускные способности a_j. Потребителей y_i свяжем с выходом z дугами (y_i,z) с пропускными способностями b_i. Остальные вершины соединим между собой дугами с соответствующими пропускными способностями в соответствии с реальным наличием связей между ними.

Возникает задача о нахождении такого распределения потока энергии (грузов, информации и т.д.) по линиям, чтобы в максимальной степени (желательно полностью) удовлетворить потребителей. Очевидно, что эта задача об отыскании потока наибольшей величины на транспортной сети D.

ЗАДАНИЕ 1.Решить задачу об источниках и потребителях, сведя ее к задаче построения максимального потока в транспортной сети и используя первый алгоритм построения максимального потока .

ЗАДАНИЕ 2.Решить задачу об источниках и потребителях, сведя ее к задаче построения максимального потока в транспортной сети и используя второй алгоритм – алгоритм меток для построения максимального потока.

b.Двудольные графы и паросочетания

Рассмотрим задачу о назначении на должности. Пусть в некотором учреждении имеется 6 вакантных должностей y₁,y₂,…,y₆ и 6 работников x₁,x₂,…,x₆. Граф D, изображенный на рис.5, иллюстрирует, какие должности y может в силу своей квалификации занимать работник x. Пусть выполнено условие: каждый работник может занимать только одну должность, и каждая работа выполняется только одним работником. Тогда решение этой задачи сводится к построению наибольшего паросочетания в данном двудольном графе.

x₁ x₂ x₃ x₄ x₅ x₆

y₁ y₂ y₃ y₄ y₅ y₆

Рис. 5.

1. Нахождение наибольшего паросочетания в двудольном графе

Граф G = (V,X) называется двудольным, если множество V его вершин допускает разбиение на два непересекающихся подмножества V₁ и V₂ (две доли), причем каждое ребро графа соединяет вершины из разных долей.

Обозначим G = (V₁,V₂, X) двудольный граф G с долями V₁ и V₂. Будем считать, что V₁ V₂.

Двудольный граф G = (V₁,V₂, X) есть полный двудольный граф, если каждая вершина из V₁ соединена ребром с каждой вершиной из V₂.

Паросочетанием Р для двудольного графа G=(V₁,V₂,X) называется любое множество попарно несмежных ребер в G.

Р есть наибольшее паросочетание для G , если число ребер в Р наибольшее среди всех возможных паросочетаний для G.

Р есть максимальное паросочетание (тупиковое) для G, если к Р нельзя добавить ни одного ребра из G, не нарушив условия паросочетаемости.

Р есть совершенное паросочетание для G, если Р имеет V₁ ребер.

Наибольшее паросочетание максимально. Совершенное паросочетание является и наибольшим, и максимальным.

Рассмотрим задачу нахождения наибольшего паросочетания в заданном двудольном графе. Это классическая задача комбинаторики, известная также под названием «задачи о назначениях».

Оказывается, что задачу нахождения наибольшего паросочетания в двудольном графе можно свести к задаче построения максимального потока в некоторой сети.

Пусть G=(V₁,V₂,X) – произвольный двудольный граф. Построим сеть S(G) с источником s, стоком t (st, s,tV₁V₂,), множеством вершин

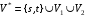, множеством дуг

,

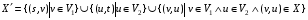и пропускной способностью c(u,v)=1 для каждой дуги (u,v) X’.

На рис.3 показано построение сети S(G) для некоторого двудольного графа.Отметим, что в сети S(G) существует максимальный нуль-единичный поток, т.е. максимальный поток φ такой, что φ(x)=0 или φ(x)=1 для каждой дуги xX’.

Теорема. Существует взаимно однозначное соответствие между паросочетаниями в G и нуль-единичными потоками в S(G), при котором паросочетанию M={(v₁,u₁), …(v_k,u_k)} мощности k (v_iV₁, u_iV₂ для 1 i  k) соответствует поток φ_М величины k, определяемый следующим образом:

φ_М (s,v_i) = φ_М (v_i,v_j)= φ_М (v_j,t)=1, 1i k,

и φ_М (x)=0 для остальных дуг x сети S(G); потоку φ величины k соответствует паросочетание М_φ, |М_φ|=k, определяемое следующим образом:

М_φ = {(v,u)| vV₁ & uV₂ & φ(v,u)=1}.

Данная теорема позволяет использовать произвольный алгоритм построения максимального потока (целочисленного) для определения наибольшего паросочетания.

Рис.3.

ЗАДАНИЕ 1.Решить задачу нахождения наибольшего паросочетания в двудольном графе, сведя ее к задаче построения максимального потока в транспортной сети и используя первый алгоритм построения максимального потока.

ЗАДАНИЕ 2.Решить задачу нахождения наибольшего паросочетания в двудольном графе, сведя ее к задаче построения максимального потока в транспортной сети и используя алгоритм меток для построения максимального потока.

Замечание. Двудольный граф задавать в виде матрицы смежности, строки которой соответствуют вершинам первой доли, а столбцы – вершинам второй доли.

c.Построение совершенного паросочетания в двудольном графе

Простая цепь С ненулевой длины в G , ребра которой попеременно лежат и не лежат в Р, называется чередующейся цепью (относительно паросочетания Р).

Эта цепь С называется Р-увеличителем, если первое и последнее ребро цепи С лежат вне Р.

С помощью Р-увеличителя паросочетание Р можно переделать в другое паросочетание Р^* для G с числом ребер в Р^* на единицу больше, чем в Р. Для этого достаточно все ребра в С, лежащие вне Р, добавить к Р, а ребра в С, лежащие в Р, удалить из Р. Для получившегося паросочетания Р^* можно снова искать увеличитель, и так далее, последовательно расширяя получающиеся паросочетания, пока это возможно.

Алгоритм

построения совершенного паросочетания

для двудольного графа

Данные: матрица смежности двудольного графа G = (U,V, X)

Результат: матрица смежности совершенного паросочетания или множество ребер (дуг), входящих в совершенное паросочетание

1. Выберем исходное паросочетание P₁, например одно ребро графа G.

2. Предположим, что паросочетание P_i=(U_i,V_i,X_i) для графа G построено. Построим паросочетание P_i+1 для G следующим образом: выбираем u из U, не принадлежащую P_i, например u₁. Если такой вершины u нет, то P_i есть совершенное паросочетание. Строим в G чередующуюся цепь _i = [u₁,v₁,u₂,v₂,...u_p,v_p] с u₁=u, в которой всякое ребро (u_i,v_i) не принадлежит X_i , а всякое ребро (v_i,u_i+1) принадлежит X_i. Если такой цепи нет, то совершенного паросочетания граф G не имеет, а паросочетание P_i является для G максимальным (тупиковым). Цепь _i есть P_i-увеличитель.

3. Выбрасываем из P_i все ребра (v_i,u_i+1) и добавляем все ребра (u_i,v_i) цепи _i. Получившееся паросочетание P_i+1 на одно ребро длиннее паросочетания P_i. Переходим к п.1.

Пример. Построим совершенное паросочетание для двудольного графа G = (U,V, X), U={u₁,u₂,u₃,u₄,u₅,u₆}, V={v₁,v₂,v₃,v₄,v₅,v₆,v₇}, матрица смежности которого имеет вид

v₁ v₂ v₃ v₄ v₅ v₆ v₇

u_{1 1 1 0 0 1 0 0}

u_{2 1 0 1 0 1 0 0}

u_{3 1 0 0 0 0 1 0}

u_{4 0 0 1 1 0 1 1}

u_{5 0 0 0 0 1 0 1}

u_{6 0 0 0 1 0 1 1}

Шаг 1. Выбираем исходное паросочетание Р₁={u₁,v₁}.

V₁ V₂ V₃ V₄ V₅ V₆ V₇

U₁ U₂ U₃ U₄ U₅ U₆

Шаг 2. Выберем вершину u₂, которая не входит в паросочетание P₁, но которая смежна с вершиной v₁, содержащейся в P₁. Далее ищем вершину v, смежную с вершиной u₁, содержащейся в Р₁. В результате получим чередующуюся цепь:

₁= [u₂,v₁,u₁,v₂]

0 1 0

1 0 1

Единица в первой строке из нулей и единиц означает, что соответствующее этой единице ребро {v₁,u₁} лежит в P₁. Убираем это ребро из P₁, а вместо него добавляем ребра {u₂,v₁}, {u₁,v₂}, соответствующие единицам второй строки. В результате получим паросочетание P₂ ={ {u₁,v₁}, {u₂,v₃} }, число ребер в котором на одно больше, чем в P₁.

Шаг 3.

V₁ V₂ V₃ V₄ V₅ V₆ V₇

U₁ U₂ U₃ U₄ U₅ U₆

Найдем чередующуюся цепь:

₂= [u₃,v₁,u₂,v_3,]

0 1 0

1 0 1

P₃={ {u₁,v₂}, {u₂,v₃},{u₃,v₁}}.

Шаг 4.

V₁ V₂ V₃ V₄ V₅ V₆ V₇

U₁ U₂ U₃ U₄ U₅ U₆

Найдем чередующуюся цепь:

₃= [u₄,v₃,u₂,v₃]

0 1 0

1 0 1

P₄={ {u₁,v₂}, {u₂,v₅},{u₃,v₁},{u₄,v₃}}.

Шаг 5.

V₁ V₂ V₃ V₄ V₅ V₆ V₇

U₁ U₂ U₃ U₄ U₅ U₆

Найдем чередующуюся цепь:

₄ = [u₅,v₅,u₂,v_1,u₃,v₆]

0 1 0 1 0

1 0 1 0 1

P₅={ {u₁,v₂}, {u₂,v₁},{u₃,v₆},{u₄,v₃},{u₅,v₅}}.

Шаг 6.

V₁ V₂ V₃ V₄ V₅ V₆ V₇

U₁ U₂ U₃ U₄ U₅ U₆

Найдем чередующуюся цепь:

₅= [u₆,v₆,u₃,v_1,u₂,v₃,u₄,v₇]

0 1 0 1 0 1 0

1 0 1 0 1 0 1

V₁ V₂ V₃ V₄ V₅ V₆ V₇

U₁ U₂ U₃ U₄ U₅ U₆

P₆={ {u₁,v₂}, {u₂,v₃}, {u₃,v₁}, {u₄,v₇},{u₅,v₅},{u₆,v₆}}. Полученное паросочетание является совершенным для исходного графа.

Задача26. Решить задачу нахождения совершенного паросочетания в двудольном графе, используя алгоритм чередующихся цепей.

1. Системы различных представителей

Пусть <A₁,…,A_n> - произвольная последовательность множеств (необязательно непересекающихся и необязательно различных). Системой различных представителей для <A₁,…,A_n> будем называть такую произвольную последовательность <а₁,…,а_n>, что 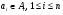и 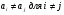. Мы будем говорить, что в такой системе различных представителей элемент a_i представляет множество A_i. Проблема существования и построения системы различных представителей известна во многих неформальных постановках. Одна из них – это так называемая «задача о комиссиях». Имеется n комиссий, причем A_i – множество членов i-й комиссии. Нужно в каждой комиссии выбрать председателя так, чтобы ни один человек не был председателем более чем в одной комиссии.

Нетрудно заметить, что задача о комиссиях сводится к частному случаю «задачи о назначениях». Действительно, создадим множества

,

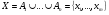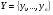
(элементы x₁,…,x_m, y₁,…,y_n попарно различны) и

.

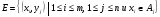Очевидно, что каждая система различных представителей <а₁,…,а_n> однозначно соответствует паросочетанию мощности n в двудольном графе D = (X,Y,E).

Задача27. Решить задачу о системе различных представителей, сведя ее к задаче построения совершенного паросочетания в двудольном графе и используя алгоритм чередующихся цепей (см. п.2.2.3).

37