Расчеты проводились с помощью программы Excel, которая позволила визуально представить результаты работы. Вданной курсовой работе приведено подробное описание этого программного продукта. Содержание
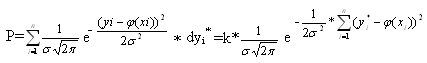
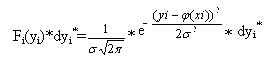
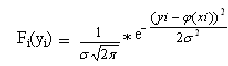
 Реферат
Реферат
В данной работе проведен обзор методов социально-экономического прогнозирования, наиболее часто применяемых в экономической практике. Выбраны четыре модели для прогнозирования потребления мяса на душу населения за год по РФ: метод наименьших квадратов (МНК), экспоненциальное сглаживание, модели Хольта, Бокса и Дженкинса. Выбранные модели дают довольно различные результаты, и лучшие результаты были получены при использовании полиномиальной модели метода наименьших квадратов и модели Хольта. Результаты вычислений представлены в таблицах. Рассчитана абсолютная ошибка прогноза и средняя относительная ошибка прогноза, коэффициент детерминации. Именно эти показатели рассматривались в качестве критерия для выбора модели, дающей наилучшее прогнозное значение интересующей нас переменной, т.е. потребления мяса на душу населения.
Расчеты проводились с помощью программы Excel, которая позволила визуально представить результаты работы. В данной курсовой работе приведено подробное описание этого программного продукта.
Стр.
Введение
5
1 Описание предметной области и постановка задачи исследования
6
2 Описание используемого математического аппарата при проведении расчетов
10
3 Описание выбранных программных продуктов
15
4 Практическая часть
21
4.1 Метод наименьших квадратов
21
4.1.1 Линейная модель МНК
21
4.1.2 Полиномиальная модель МНК
23
4.1.3 Экспоненциальная модель МНК
24
4.2 Экспоненциальное сглаживание
26
4.2 Двухпараметрическая модель Хольта
30
4.3 Трехпараметрическая модель Бокса и Дженкинса
34
5 Выбор лучшей модели
36
Заключение
38
Список использованных источников
39
Введение
Практически каждое предприятие, большое или маленькое, частное или государственное, явно или неявно пользуется прогнозами, потому что каждое предприятие должно планировать будущее, о котором оно пока ничего не знает. Прогнозы необходимы в финансировании, маркетинге, подборе кадров и различных производственных областях, в правительственных и коммерческих организациях, в маленьких социальных клубах и национальных политических партиях.
Прогнозирование – это способ научного предвидения, в котором используется как накопленный в прошлом опыт, так и текущие допущения насчет будущего с целью его определения. Результатом является прогноз, то есть научно обоснованное суждение о возможных состояниях объекта в будущем, об альтернативных путях и сроках его существования.
Прогнозирование определяет реальность и благоприятность для хозяйственной структуры поставленных перед ней целей.
Целью данной курсовой работы является рассмотрение наиболее эффективных методов социально-экономических прогнозов и осуществление прогнозирования общего числа страховых организаций, так как российский рынок мяса и мясных продуктов является самым крупным сектором продовольственного рынка: за ним следует зерновой, затем молочный. Его роль определяется не только растущими объемами производства, спроса и потребления мясных продуктов, но и их значимостью как основного источника белка животного происхождения в рационе человека.
В настоящее время по уровню потребления мясопродукции на душу населения Россия еще значительно отстает от развитых стран, однако этот показатель постепенно увеличивается, что говорит о росте благосостояния населения страны, вместе с которым будет неуклонно расти емкость мясного рынка.
1 Описание предметной области и постановка задачи исследования
До 1991 года СССР предпочитал закупать за рубежом не дорогое мясо, а зерно для производства кормов. Тем самым он экономил деньги и давал работу отечественному животноводству. Правда, мясо «дотировалось» два раза: сначала государство, закупив зерно в США, по льготным ценам отдавало его производителям кормов. Затем государство, покупая мясо у животноводов по 4 рубля за килограмм, затем реализовывало его в рознично торговле по 1,9 рубля. Правда, за счет высокого платежеспособного спроса мясо стало дефицитом: его быстро сметали с прилавков или торговали им «из-под полы». Государство в СССР так и не решилось отменить дотации на мясо и наполнить им магазины, повысив цены на него до 5-6 рублей.
С 1991 года это система рухнула: мясоперерабатывающие заводы принялись закупать мясо прямо за границей. В постсоветский период импорт мяса увеличивался год от года. Началось массовое производство фальсифицированной низкокачественной мясопродукции. Этот факт обычно сопровождается идеологически окрашенными комментариями, сводящимися к констатации отрицательной динамики отрасли в 1990-е годы. Действительно, производство и потребление мяса в России неуклонно сокращалось на протяжении 1990-х годов и стало расти в 2000-е.
Одной из основных тенденций развития мирового рынка мяса на сегодняшний день является недостаточный для обеспечения нужд потребителей уровень производства. Производители мяса сталкиваются с проблемой ограниченности кормовой базы для животноводства, которая является актуальной и для России. Недостаточное производство мясного сырья в свою очередь создает проблемы для развития пищевой промышленности. В настоящее время Россия не в состоянии полностью обеспечить себя мясом отечественного производства. Соответственно переход мясоперерабатывающей индустрии на отечественное сырье в ближайшее время невозможен. В связи с этим можно сделать вывод, что в ближайшем будущем импортные поставки будут играть определяющую роль в обеспечении отечественных предприятий сырьем. Несмотря на это высокий потенциал российского мясной отрасли и программы правительства, направленные на развитие и поддержку отечественного производителя, позволяют надеяться на позитивные изменения в данном секторе экономики.
В ближайшей перспективе у отечественных животноводов появляется шанс укрепить свои позиции, как на российском, так и международном рынках. Быстрее всех будет развиваться птицеводство, которое характеризуется самой высокой оборачиваемостью капитала и коротким сроком окупаемости. Период окупаемости свиноводческих хозяйств составляет пять лет, производство говядины окупается лишь за десять. Исходя из тенденций последних лет, рынок свинины можно охарактеризовать как насыщенный и близкий к стабильности, в то время как на рынке говядины наблюдается явный дефицит предложения. Рост производства свинины обусловлен появлением ряда крупных инвестиционных проектов. В то же время инвестиционные проекты по выращиванию КРС просто отсутствуют. На рынке говядины наблюдается увеличение доли импорта, рост цен, обусловленный недостаточным предложением на внутреннем рынке, снижение потребительского спроса на мясо в связи с низким уровнем реальных денежных доходов населения.
Потребление мяса в России стабильно увеличивается. Поскольку отечественные производители мяса не могут в полной мере удовлетворить спрос, актуальным остается импорт мяса.
Отечественные производители мяса наращивают объемы производства свинины и мяса птицы. Производство КРС находится в упадке. Следовательно, наиболее выгодным является импорт говядины (более низкие пошлины, по сравнению с пошлинами на свинину и мясо птицы, отсутствие конкуренции со стороны отечественных производителей).
Основным экспортером говядины является Бразилия. В 2006 году экспорт говядины из Бразилии был закрыт по причине карантина.
В связи с этим, импортеры существенно увеличили объем вывоза говядины из Аргентины. После чего, президент Аргентины ввел запрет на экспорт из страны говядины сроком на полгода. Причина - слишком большой вывоз этой продукции из страны, повлекший рост цен на мясо на местном рынке Аргентины.
Экспорт говядины из Уругвая, Парагвая и стран ЕС в полной мере не мог покрыть образовавшийся спрос (недостаточные объемы производства говядины) и цены на мясо из этих стран значительно выше цен на мясо из Бразилии и Аргентины.
Таким образом, вследствие принятой Аргентиной защитной меры образовался дефицит говядины в России и рост цен на нее. В этой ситуации в выигрыше оказались компании-трейдеры, имеющие запасы на складах.
После того, как запрет на экспорт из Бразилии был снят, и угроза образования дефицита говядины пропала, в России последовало снижение цен на говядину.
В целом, рынок мясной продукции обладает высокой емкостью и характеризуется стабильным спросом, высокой инвестиционной привлекательностью и жестким уровнем конкуренции местных и зарубежных игроков.
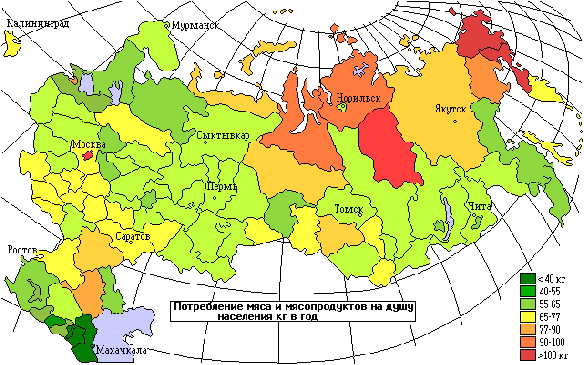
Если проанализировать потребление мяса и мясопродуктов в регионах России, то можно отметить отчетливую биполярность. Максимумы потребления этих продуктов приходятся на столичные центры (Москва и С-Петербург) и на северные регионы страны, где значительную часть составляет промыслово-скотоводческое население.
Помимо политически традиционной поддержки столичных центров на высоком уровне потребления мяса, здесь сказывается еще один серьезный фактор - высокая концентрация наиболее трудоспособного и экономически активного населения. Физиологическая потребность в мясных продуктах у взрослых мужчин выше средней на 10%, а у молодых и того выше - на 38%. Кроме этого в условиях лучшей адаптации к кризису и более высоких заработков население столичных центров располагало и более высокой покупательной способностью.
2 Описание используемого математического аппарата
при проведении расчетов
2.1 Метод наименьших квадратов (МНК)
Метод наименьших квадратов позволяет относительно просто определить аналитическую зависимость одного показателя от другого: y=φ(x). Имея такую функциональную зависимость, легко определить значение Y при любом значении x, т.е. получить прогнозное значение Y при заданном значении х.
Вывод формул МНК. Пусть имеем статистические данные о параметре y в зависимости от х. Эти данные представим в таблице ниже:
х
х1
х2
…..
хi
…..
хn
y*
y1*
y2*
......
yi*
…..
yn*
Метод наименьших квадратов позволяет при заданном типе зависимости y=φ(x) так выбрать ее числовые параметры, чтобы кривая y=φ(x) наилучшим образом отображала экспериментальные данные по заданному критерию. Рассмотрим обоснование с точки зрения теории вероятностей для математического определения параметров, входящих в φ(x).
Предположим, что истинная зависимость y от х в точности выражается формулой y=φ(x). Рассмотрим какое-нибудь значение аргумента хi. Результат опыта есть случайная величина yi,распределенная по нормальному закону с математическим ожиданием φ(xi) и со средним квадратическим отклонением σi, характеризующим ошибку измерения. Пусть точность измерения во всех точках х=(х1, х2, …, хn) одинакова, т.е. σ1=σ2=…=σn=σ. Тогда нормальный закон распределения Yi имеет вид:
(1)
В результате ряда измерений произошло следующее событие: случайные величины (y1*, y2*, …, yn*). Поставим следующую задачу.
Задача МНК. Подобрать математические ожидания φ(x1), φ(x2), …, φ(xn) так, чтобы вероятность этого события была максимальной. Так как величины Yi непрерывны, то говорят не о вероятностях событий Yi=yi*, а о вероятностях того, что Yi примут значения из интервала (yi*,yi*+dyi*), т.е.
Вероятность P того, что система случайных величин (y1, y2, …, yn) примет совокупность значений, лежащих в пределах (yi*,yi*+dyi*), i=1, 2, …, n, с учетом того, что измерения проводятся независимо друг от друга, равна произведению вероятностей Fi(yi)*dyi* для всех значений i:
(2)
Где k – коэффициент, не зависящий от φ(xi).
Требуется выбрать математические ожидания
φ(x1), φ(x2), …, φ(xn) так, чтобы выражение (2) достигало максимума. Это возможно, когда выполнено условие
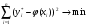 . (3)
. (3)
Отсюда получаем требование метода наименьших квадратов: для того чтобы данная совокупность наблюдаемых значений (y1*, y2*, …, yn*) была наивероятнейшей, нужно выбрать функцию φ(x) так, чтобы сумма квадратов отклонений наблюдаемых значений yi* от φ(xi) была наименьшей.
При решении практических задач зависимость y=φ(x) задается в виде y=φ(x,a1, a2, …, am), где a1, a2, …, am – числовые параметры, которые необходимо определить. Учитывая соотношение (3), получим
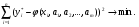 (4)
(4)
Продифференцируем выражение (4) по a1, a2, …, am и прировняем полученные производные нулю. Получим следующую систему уравнений:
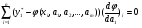 ,
,
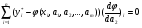 ,
,
… … … … … … … … … … ; (5)
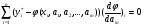 ,
,
где 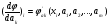 - значения частной производной функции φ по аk в точке хi.
- значения частной производной функции φ по аk в точке хi.
Отметим, что в общем случае систему (5) решить нельзя, так как неизвестен вид функции φ(x,a1, a2, …, am). При решении практических задач зависимость y от x ищут в виде линейной комбинации известных функций с коэффициентами a1, a2, …, am, а именно: 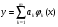 . Подставив значение φk(х) в (5), решаем эту систему и находим a1, a2, …, am.
. Подставив значение φk(х) в (5), решаем эту систему и находим a1, a2, …, am.
Рассмотрим один из частных случаев МНК: пусть зависимость y от х выражается линейной функцией y=a1+a2x. Тогда значения коэффициентов a1 и a2 находятся по следующим формулам:
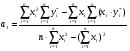 ;
; 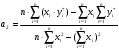 (6)
(6)
2.2 Экспоненциальное сглаживание
Экспоненциальное сглаживание – один из простейших и распространенных приемов выравнивания ряда. В его основе лежит расчет экспоненциальных средних.
При исследовании временного ряда xt экспоненциальное сглаживание проводится по формуле:
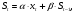 (8)
(8)
где хt – текущий член временного ряда в момент времени t;
St – значение экспоненциальной средней в момент времени t;
α – параметр адаптации (параметр сглаживания),
0< α<1, β=1-α.
В качестве начальных условий для применения экспоненциального сглаживания рекомендуется выбирать следующие значения:
- среднее арифметическое всех имеющихся значений (или части значений) временного ряда;
- среднее геометрическое всех имеющихся значений временного ряда;
- значения, выбранные из статистики, полученной при наблюдении за аналогами изучаемого явления.
Величина St оказывается взвешенной суммой всех членов ряда. Причем веса падают экспоненциально в зависимости от давности наблюдения.
Экспоненциальная средняя St имеет то же математическое ожидание, что и ряд х, но меньшую дисперсию. Чем меньше α, тем в большей степени сокращается дисперсия экспоненциальной средней.
2.3 Двухпараметрическая модель Хольта
При исследовании численности населения используется двухпараметрическая модель Хольта.
Простейшая модификация двухпараметрической модели Хольта выглядит следующим образом:
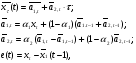
где: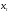 - временной ряд;
- временной ряд;
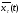 - прогнозное значение врем. ряда в точке t на
- прогнозное значение врем. ряда в точке t на 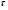 шагов вперед;
шагов вперед;
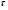 - шаг прогноза;
- шаг прогноза;
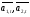 - коэффициенты;
- коэффициенты;
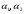 - параметры адаптации,
- параметры адаптации, 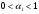 и
и 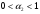 ;
;
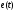 - ошибка прогноза.
- ошибка прогноза.
2.4 Трехпараметрическая модель Бокса и Дженкинса
Модель Бокса и Дженкинса является одним из вариантов “усовершенствованной” модели Хольта за счет включения в расчетные формулы разности ошибок прогнозов:
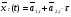 (1)
(1)
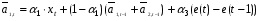 (2)
(2)
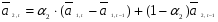 (3)
(3)
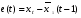 (4)
(4)
где 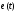 – ошибка прогноза.
– ошибка прогноза.
Обобщенная модель Бокса и Дженкинса может применяться для прогнозирования нестационарных временных рядов, так как содержит не только операцию сглаживания скользящим средним, но и элементы авторегрессии.
Модель основывается на гипотезе, что изучаемый процесс является выходом линейного фильтра, на вход которого подан процесс белого шума, т.е. что член ряда 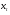 является взвешенной суммой текущего и предыдущих значений входного потока.
является взвешенной суммой текущего и предыдущих значений входного потока.
Если последовательность предыдущих значений конечна или бесконечна, но сходится, то фильтр называется устойчивым, а процесс 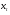 - стационарным.
- стационарным.
3 Описание выбранных программных продуктов
Для расчетов будут использоваться СПП STATISTICA и MS Excel.
MS Excel - средство для работы с электронными таблицами, намного превышающее по своим возможностям существующие редакторы таблиц. MS Excel - это простое и удобное средство, позволяющее проанализировать данные и, при необходимости, проинформировать о результате заинтересованную аудиторию, используя Internet.
Достоинства Microsoft Excel:
Эффективность анализа данных;
Быстрый и эффективный анализ, удобные средства для работы с данными (мастер сводных таблиц позволяет быстро обрабатывать большие массивы данных и получать итоговые результаты в удобном виде);
Механизм автокоррекции формул автоматически распознает и исправляет ошибки при введении формул;
Использование естественного языка при написании формул.
Богатство средств форматирования и отображения данных
Новые средства форматирования делают оформление таблиц более ярким и понятным (возможности слияния ячеек в электронной таблице, поворот текста в ячейке на любой угол);
Новый и дополненный Мастер создания диаграмм позволяет сделать представление данных в таблицах более наглядным (более удобный и мощный мастер создания диаграмм, новые типы диаграмм - диаграммы в виде круглых столбиков, тетраэдров, в виде «бубликов» и др.);
Совместное использование данных и работа над документами;
Microsoft Excel обеспечивает возможность одновременной работы нескольких пользователей над одним документом;
Обмен данными и работа в Internet;
Теперь возможно использовать самые свежие данные путем получения их в виде электронных таблиц прямо с Web-серверов в Internet;
Возможность использовать встроенный Internet Assistant для преобразования таблицы в формат HTML и публикации на Web-сервере.
Пакет STATISTICA был создан в начале 1990-х годов сразу для среды Windows. В пакете нашли отражение многие последние достижения теоретической и прикладной статистики.
У пакета есть специальная версия для обучения основам статистических методов – Studеnt Еditiоn оf STATISTICA. Эта версия позволяет анализировать файлы данных, включающих не более 400 наблюдений, и представляет собой урезанный вариант пакета.
Основная версия пакета может дополнительно комплектоваться специализированными модулями: Роwеr Analysis (планирование статистических исследовании), Nеural Nеtwоrks (нейросетевой анализ) и др.
С помощью реализованных в системе STATISTICA мощных языков программирования, снабженных специальными средствами поддержки, легко создаются законченные пользовательские решения и встраиваются в различные другие приложения или вычислительные среды. Очень трудно представить себе, что кому-то могут понадобиться абсолютно все статистические процедуры и методы визуализации, имеющиеся в системе STATISTICA, однако опыт многих людей, успешно работающих с пакетом, свидетельствует о том, что возможность доступа к новым, нетрадиционным методам анализа данных помогает находить новые способы проверки рабочих гипотез и исследования данных.
STATISTICA является наиболее динамично развивающимся статистическим пакетом и по многочисленным рейтингам является мировым лидером на рынке статистического программного обеспечения. СПП STATISTICA является универсальной системой, предназначенной для статистического анализа и визуализации данных, управления базами данных и разработки пользовательских приложений, содержащей широкий набор процедур анализа для применения в научных исследованиях, технике, бизнесе.
Она состоит из следующих основных компонент, объединенных в рамках одной системы:
электронных таблиц для ввода и задания исходных данных;
специальных таблиц для вывода численных результатов анализа;
графической системы для визуализации данных и результатов статистического анализа;
набора специализированных статистических модулей, в которых собраны группы логически связанных между собой статистических процедур;
специального инструментария для подготовки отчетов.
Статистический анализ данных в системе STATISTICA может быть разбит на следующие основные этапы:
ввод данных в электронную таблицу с исходными данными и их предварительное преобразование перед анализом;
визуализация данных при помощи того или иного типа графиков;
применение конкретной процедуры статистической обработки;
вывод результатов анализа в виде графиков и электронных таблиц с численной и текстовой информацией.
Пакет содержит следующие модули:
Basic Statistic/Tables – Основные статистики и таблицы: позволяет провести предварительную обработку данных, осуществить разведочный анализ, определить зависимости между переменными, разбить их различными способами на группы;
Nonparametrics/Distrib. – Модуль Непараметрическая статистика/Распределеня: дает возможность проверить гипотезы о характере распределения ваших данных;
ANOVA/MANOVA – Модуль дисперсионного анализа: представляет собой набор процедур общего одномерного и многомерного дисперсионного и ковариационного анализа;
Multiple Regression - Модуль Множественная регрессия: помогает построить зависимости между многомерными переменными, подобрать простую линейную модель и оценить ее адекватность;
Nonlinear Estimation – Модуль Нелинейное оценивание: предоставляет возможность определения нелинейной зависимости в данных и подгонки к ним функциональных кривых;
Time Series/Forecasting – Анализ временных рядов и прогнозирование: общее назначение модуля – построить простую модель, описывающую ряд, сгладить его, спрогнозировать будущие значения временного ряда на основе наблюдаемых до данного момента, построить регрессионные зависимости одного ряда от другого, провести спектральный или Фурье – анализ ряда;
Claster Analysis – Модуль Кластерный анализ: позволяет произвести сложную иерархическую классификацию данных или выделить в них кластеры;
Data Management/MFM - Управление данными: специализированный модуль, который содержит большое количество вспомогательных процедур по работе с данными (иерархическая сортировка, проверка, категоризация и ранжирование и др.);
Factor Analysis – Модуль Факторный анализ: дает возможность сжать данные или выделить основные общие факторы, влияющие на наблюдаемые характеристики сложного объекта и объясняющие связи между ними;
Canonical Analysis – Модуль Канонический анализ: включает в себя широкий набор процедур для выполнения канонического корреляционного анализа, исследования связи между двумя множествами переменных;
Multidimensional Scaling – Модуль Многомерное шкалирование: помогает представить данные о близости объектов какой-либо простой пространственной моделью, в которой объекты интерпретируются, например, как города на обычной карте, а различия между ними есть просто расстояния, в частности данные о странах, политических партиях и т.д., и всесторонне диагностировать модель;
SEPATH – Модуль Моделирование структурными уравнениями: позволяет строить и тестировать различные модели, объясняющие структуру связей между наблюдаемыми переменными;
Reliability/Item Analysis – Модуль Анализ надежности: включает широкий набор процедур для разработки и вычислений надежности сложных объектов на основе результатов обследований и диагностики отдельных узлов;
Discriminant Analysis - Модуль Дискриминантный анализ: позволяет построить на основе ряда предположений классификационное правило отнесения объекта к одному из нескольких классов, минимизируя некоторый разумный критерий;
Log-linear Analysis – Модуль Лог-линейный анализ: проводит анализ сложных многоуровневых таблиц;
Survival Analysis – Модуль Анализ длительностей жизни: предлагает обширный набор методов анализа данных из социологии, биологии, медицины, так же, как процедуры, используемые в инженерии и маркетинге;
Commmand Language (SCL) – Командный язык STATISTICA: позволяет автоматизировать рутинные процессы обработки данных в системе;
STATISTICA File Server – позволяет быстро открыть для просмотра/редактирования как графики и таблицы, так и отчеты.
Выбор системы STATISTICA в качестве инструмента для обработки данных может быть обусловлен возможностью проведения наиболее полного анализа, т.к. система содержит все необходимые нам статистические процедуры.
Основные преимущества системы STATISTICA:
содержит полный набор классических методов анализа данных: от основных классических методов статистики, до самых современных, что позволяет гибко организовывать анализ;
является средством построения приложений в конкретных областях;
отвечает всем стандартам Windows, что позволяет сделать анализ высокоинтерактивным;
система может быть интегрирована в Интернет;
поддерживает web-форматы:HTML, JPEG, PNG;
данные системы STATISTICA легко конвертировать в различные базы данных и электронные таблицы;
поддерживает высококачественную графику, позволяющую эффективно визуализировать данные и проводить графический анализ;
является открытой системой: содержит языки программирования, которые позволяют расширить систему, запускать ее из других Windows-приложений, например из Excel;
используются разнообразные методы, позволяющие провести всесторонне исследование ретроспективных данных (в виде временных рядов);
доступны различные возможности преобразования временных рядов;
позволяют построить объективный прогноз данных, который включает в себя вычисление верхних и нижних границ, в которых, можно утверждать, что с определенной вероятностью лежат значения прогнозируемых показателей.
4 Практическая часть
У нас имеются данные по потреблению мяса и мясопродуктов в пересчете на мясо на душу населения за последние 20 лет по полугодиям, РФ (кг):
I полуг. 1990
75,0
I полуг. 2000
45,0
II полуг. 1990
72,0
II полуг. 2000
45,0
I полуг. 1991
69,0
I полуг. 2001
46,0
II полуг. 1991
64,5
II полуг. 2001
47,0
I полуг. 1992
60,0
I полуг. 2002
48,5
II полуг. 1992
59,5
II полуг. 2002
50,0
I полуг. 1993
59,0
I полуг. 2003
51,0
II полуг. 1993
58,0
II полуг. 2003
52,0
I полуг. 1994
57,0
I полуг. 2004
53,0
II полуг. 1994
56,0
II полуг. 2004
54,0
I полуг. 1995
55,0
I полуг. 2005
54,5
II полуг. 1995
53,0
II полуг. 2005
55,0
I полуг. 1996
51,0
I полуг. 2006
57,0
II полуг. 1996
50,5
II полуг. 2006
59,0
I полуг. 1997
50,0
I полуг. 2007
60,5
II полуг. 1997
50,0
II полуг. 2007
62,0
I полуг. 1998
49,0
I полуг. 2008
64,0
II полуг. 1998
48,0
II полуг. 2008
66,0
I полуг. 1999
46,5
I полуг. 2009
66,5
II полуг. 1999
45,0
II полуг. 2009
67,0
Необходимо спрогнозировать сколько мяса будет потреблять россиянин в I и II полугодиях 2010 года. Будем использовать МНК, экспоненциальное сглаживание, модели Хольта, Бокса и Дженкинса.
4.1 Метод наименьших квадратов
4.1.1 Линейная модель МНК
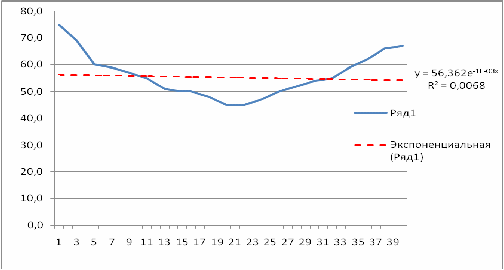
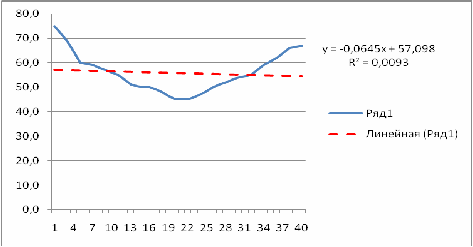
Параметры линейной зависимости 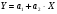 определяются в пакете MS Excel. При построении линии тренда была получена следующая зависимость: y= -0,0645*x+57,098 . Коэффициент детерминации для тренда линейного вида
определяются в пакете MS Excel. При построении линии тренда была получена следующая зависимость: y= -0,0645*x+57,098 . Коэффициент детерминации для тренда линейного вида 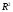 составляет 0,0093, что говорит об описании исходных данных линией тренда меньше, чем на 1 %.
составляет 0,0093, что говорит об описании исходных данных линией тренда меньше, чем на 1 %.
Это объясняется тем, что в связи с нестабильной экономической ситуацией в стране, в 2000-е годы резко снизилось потребление мяса.
Расчет средней абсолютной и среднеквадратической ошибок модели:
t
Y
t*t
t*Y
Y*
|Y-Y*|
|Y-Y*|^2
1
75,0
1
75
57,034
17,9665
322,8
2
72,0
4
144
56,969
15,031
225,93
3
69,0
9
207
56,905
12,0955
146,3
4
64,5
16
258
56,84
7,66
58,676
5
60,0
25
300
56,776
3,2245
10,397
6
59,5
36
357
56,711
2,789
7,7785
7
59,0
49
413
56,647
2,3535
5,539
8
58,0
64
464
56,582
1,418
2,0107
9
57,0
81
513
56,518
0,4825
0,2328
10
56,0
100
560
56,453
0,453
0,2052
11
55,0
121
605
56,389
1,3885
1,9279
12
53,0
144
636
56,324
3,324
11,049
13
51,0
169
663
56,26
5,2595
27,662
14
50,5
196
707
56,195
5,695
32,433
15
50,0
225
750
56,131
6,1305
37,583
16
50,0
256
800
56,066
6,066
36,796
17
49,0
289
833
56,002
7,0015
49,021
18
48,0
324
864
55,937
7,937
62,996
19
46,5
361
883,5
55,873
9,3725
87,844
20
45,0
400
900
55,808
10,808
116,81
21
45,0
441
945
55,744
10,7435
115,42
22
45,0
484
990
55,679
10,679
114,04
23
46,0
529
1058
55,615
9,6145
92,439
24
47,0
576
1128
55,55
8,55
73,102
25
48,5
625
1212,5
55,486
6,9855
48,797
26
50,0
676
1300
55,421
5,421
29,387
27
51,0
729
1377
55,357
4,3565
18,979
28
52,0
784
1456
55,292
3,292
10,837
29
53,0
841
1537
55,228
2,2275
4,9618
30
54,0
900
1620
55,163
1,163
1,3526
31
54,5
961
1689,5
55,099
0,5985
0,3582
32
55,0
1024
1760
55,034
0,034
0,0012
33
57,0
1089
1881
54,97
2,0305
4,1229
34
59,0
1156
2006
54,905
4,095
16,769
35
60,5
1225
2117,5
54,841
5,6595
32,03
36
62,0
1296
2232
54,776
7,224
52,186
37
64,0
1369
2368
54,712
9,2885
86,276
38
66,0
1444
2508
54,647
11,353
128,89
39
66,5
1521
2593,5
54,583
11,9175
142,03
40
67,0
1600
2680
54,518
12,482
155,8
41
Прогнозн. значения
I полуг. 2010
54,454
42
II полуг. 2010
54,389
Средняя абсолютная ошибка
6,3543
Среднеквадратическая ошибка
59,3
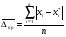 =6,3543;
=6,3543; 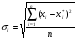 =59,3.
=59,3.
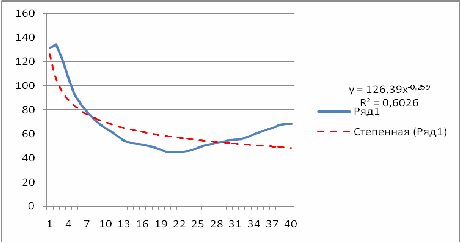
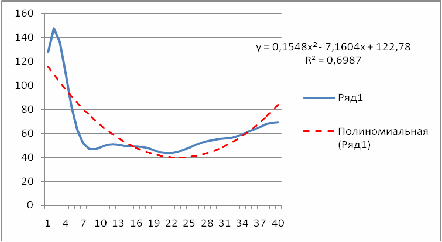
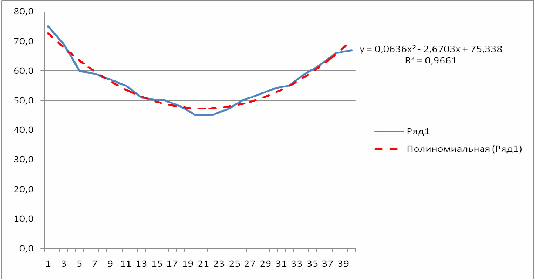
4.1.2 Полиномиальная модель МНК
Полином второго порядка 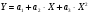 строится аналогично линейной функции с помощью метода наименьших квадратов и встроенным функциям ППП MS Excel. Уравнение тренда имеет вид: y=0,06365*х2 – 2,6703*х + 75,338. Коэффициент детерминации равен 0,9661.
строится аналогично линейной функции с помощью метода наименьших квадратов и встроенным функциям ППП MS Excel. Уравнение тренда имеет вид: y=0,06365*х2 – 2,6703*х + 75,338. Коэффициент детерминации равен 0,9661.
Расчет средней абсолютной и среднеквадратической ошибок модели:
t
Y
t*t
t*Y
Y*
|Y-Y*|
|Y-Y*|^2
I полуг. 1990
1
75,0
1
75
72,7313
2,2687
5,1
II полуг. 1990
2
72,0
4
144
70,2518
1,7482
3,1
I полуг. 1991
3
69,0
9
207
67,8995
1,1005
1,2
II полуг. 1991
4
64,5
16
258
65,6744
1,1744
1,4
I полуг. 1992
5
60,0
25
300
63,5765
3,5765
12,8
II полуг. 1992
6
59,5
36
357
61,6058
2,1058
4,4
I полуг. 1993
7
59,0
49
413
59,7623
0,7623
0,6
II полуг. 1993
8
58,0
64
464
58,046
0,046
0,0
I полуг. 1994
9
57,0
81
513
56,4569
0,5431
0,3
II полуг. 1994
10
56,0
100
560
54,995
1,005
1,0
I полуг. 1995
11
55,0
121
605
53,6603
1,3397
1,8
II полуг. 1995
12
53,0
144
636
52,4528
0,5472
0,3
I полуг. 1996
13
51,0
169
663
51,3725
0,3725
0,1
II полуг. 1996
14
50,5
196
707
50,4194
0,0806
0,0
I полуг. 1997
15
50,0
225
750
49,5935
0,4065
0,2
II полуг. 1997
16
50,0
256
800
48,8948
1,1052
1,2
I полуг. 1998
17
49,0
289
833
48,3233
0,6767
0,5
II полуг. 1998
18
48,0
324
864
47,879
0,121
0,0
I полуг. 1999
19
46,5
361
883,5
47,5619
1,0619
1,1
II полуг. 1999
20
45,0
400
900
47,372
2,372
5,6
I полуг. 2000
21
45,0
441
945
47,3093
2,3093
5,3
II полуг. 2000
22
45,0
484
990
47,3738
2,3738
5,6
I полуг. 2001
23
46,0
529
1058
47,5655
1,5655
2,5
II полуг. 2001
24
47,0
576
1128
47,8844
0,8844
0,8
I полуг. 2002
25
48,5
625
1212,5
48,3305
0,1695
0,0
II полуг. 2002
26
50,0
676
1300
48,9038
1,0962
1,2
I полуг. 2003
27
51,0
729
1377
49,6043
1,3957
1,9
II полуг. 2003
28
52,0
784
1456
50,432
1,568
2,5
I полуг. 2004
29
53,0
841
1537
51,3869
1,6131
2,6
II полуг. 2004
30
54,0
900
1620
52,469
1,531
2,3
I полуг. 2005
31
54,5
961
1689,5
53,6783
0,8217
0,7
II полуг. 2005
32
55,0
1024
1760
55,0148
0,0148
0,0
I полуг. 2006
33
57,0
1089
1881
56,4785
0,5215
0,3
II полуг. 2006
34
59,0
1156
2006
58,0694
0,9306
0,9
I полуг. 2007
35
60,5
1225
2117,5
59,7875
0,7125
0,5
II полуг. 2007
36
62,0
1296
2232
61,6328
0,3672
0,1
I полуг. 2008
37
64,0
1369
2368
63,6053
0,3947
0,2
II полуг. 2008
38
66,0
1444
2508
65,705
0,295
0,1
I полуг. 2009
39
66,5
1521
2593,5
67,9319
1,4319
2,1
II полуг. 2009
40
67,0
1600
2680
70,286
3,286
10,8
41
Прогнозн. значения
I полуг. 2010
72,7673
42
II полуг. 2010
75,3758
Средняя абсолютная ошибка
1,142405
Среднеквадратичская ошибка
2,0
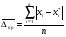 =1,142405;
=1,142405; 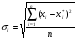 =2,0.
=2,0.
Произошло значительное уменьшение средней абсолютной и среднеквадратической ошибок по сравнению с линейной моделью.
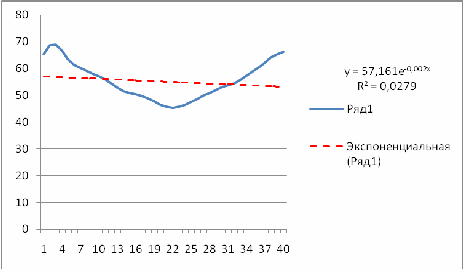
4.1.3 Экспоненциальная модель МНК
Экспоненциальная функция 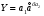 строится с использованием средств MS Excel и имеет вид х=56,362*е-1Е-03х, коэффициент детерминации очень низок, экспоненциальная функция описывает исходные данные на 0,7%.
строится с использованием средств MS Excel и имеет вид х=56,362*е-1Е-03х, коэффициент детерминации очень низок, экспоненциальная функция описывает исходные данные на 0,7%.
Расчет средней абсолютной и среднеквадратической ошибок модели:
t
Y
t*t
t*Y
Y*
|Y-Y*|
|Y-Y*|^2
1
75,0
1
75
56,30557
18,69443
349,4819
2
72,0
4
144
56,24929
15,75071
248,0849
3
69,0
9
207
56,19307
12,80693
164,0175
4
64,5
16
258
56,1369
8,363097
69,9414
5
60,0
25
300
56,08079
3,919206
15,36018
6
59,5
36
357
56,02474
3,475259
12,07742
7
59,0
49
413
55,96874
3,031256
9,188511
8
58,0
64
464
55,9128
2,087196
4,356389
9
57,0
81
513
55,85692
1,143081
1,306635
10
56,0
100
560
55,80109
0,19891
0,039565
11
55,0
121
605
55,74532
0,745317
0,555497
12
53,0
144
636
55,6896
2,689599
7,233943
13
51,0
169
663
55,63394
4,633937
21,47337
14
50,5
196
707
55,57833
5,078331
25,78945
15
50,0
225
750
55,52278
5,522781
30,50111
16
50,0
256
800
55,46729
5,467286
29,89121
17
49,0
289
833
55,41185
6,411846
41,11177
18
48,0
324
864
55,35646
7,356462
54,11753
19
46,5
361
883,5
55,30113
8,801133
77,45994
20
45,0
400
900
55,24586
10,24586
104,9776
21
45,0
441
945
55,19064
10,19064
103,8492
22
45,0
484
990
55,13548
10,13548
102,7279
23
46,0
529
1058
55,08037
9,08037
82,45313
24
47,0
576
1128
55,02532
8,025318
64,40572
25
48,5
625
1212,5
54,97032
6,47032
41,86504
26
50,0
676
1300
54,91538
4,915377
24,16093
27
51,0
729
1377
54,86049
3,860489
14,90338
28
52,0
784
1456
54,80566
2,805656
7,871705
29
53,0
841
1537
54,75088
1,750878
3,065572
30
54,0
900
1620
54,69615
0,696154
0,484631
31
54,5
961
1689,5
54,64149
0,141485
0,020018
32
55,0
1024
1760
54,58687
0,413129
0,170675
33
57,0
1089
1881
54,53231
2,467688
6,089486
34
59,0
1156
2006
54,47781
4,522194
20,45023
35
60,5
1225
2117,5
54,42336
6,076644
36,9256
36
62,0
1296
2232
54,36896
7,63104
58,23278
37
64,0
1369
2368
54,31462
9,685382
93,80663
38
66,0
1444
2508
54,26033
11,73967
137,8198
39
66,5
1521
2593,5
54,2061
12,2939
151,14
40
67,0
1600
2680
54,15192
12,84808
165,0732
41
Прогнозн. значения
I полуг. 2010
54,09779
42
II полуг. 2010
54,04372
Средняя абсолютная ошибка
6,304313
Среднеквадратическая ошибка
59,6
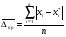 =6,304;
=6,304; 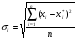 =59,6.
=59,6.
4.2 Экспоненциальное сглаживание
Применим к рассматриваемому временному ряду экспоненциальное сглаживание, используя формулу: 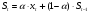 .
.
Значит, для t=1 получаем формулу: 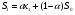 . Сначала необходимо определить начальное значение S0 как среднее значение прогнозного ряда. Шаг прогноза в нашем случае равен 1. Повторяем проделанные шаги несколько раз и формируем таким образом прогнозный ряд на основе экспоненциального сглаживания для экспоненциальной адаптивной модели. Большое влияние на точность прогноза влияет параметр адаптации . Поэтому рассмотрим сглаженные ряды для нескольких значений параметра сглаживания, а именно для =0,25 =0,5 и =0,75. Все расчеты представим в виде таблиц.
. Сначала необходимо определить начальное значение S0 как среднее значение прогнозного ряда. Шаг прогноза в нашем случае равен 1. Повторяем проделанные шаги несколько раз и формируем таким образом прогнозный ряд на основе экспоненциального сглаживания для экспоненциальной адаптивной модели. Большое влияние на точность прогноза влияет параметр адаптации . Поэтому рассмотрим сглаженные ряды для нескольких значений параметра сглаживания, а именно для =0,25 =0,5 и =0,75. Все расчеты представим в виде таблиц.
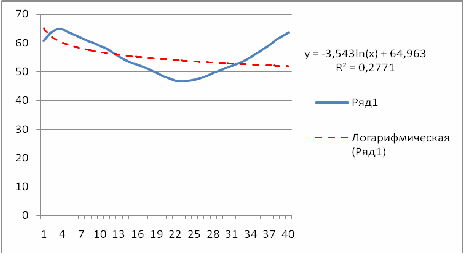
Рассмотрим экспоненциальное сглаживание с коэффициентом адаптации =0,25, тогда график потребления мясопродуктов будет так:
В этом случае коэффициент детерминации составляет 0,2771, т.е. модель на 28 % описывает исходные данные.
t
Y
Y cглаж. при 0,25
Прогноз
|Y-Y*|
|Y-Y*|^2
1
75,0
60,58125
58,1492902
16,8507098
283,9464209
2
72,0
63,43594
57,9751037
14,0248963
196,6977152
3
69,0
64,82695
57,8014391
11,1985609
125,4077673
4
64,5
64,74521
57,6282946
6,87170542
47,22033537
5
60,0
63,55891
57,4556688
2,54433123
6,473621431
6
59,5
62,54418
57,2835601
2,21643995
4,912606046
7
59,0
61,65814
57,1119669
1,88803311
3,564669026
8
58,0
60,7436
56,9408877
1,05911226
1,121718788
9
57,0
59,8077
56,7703211
0,22967895
0,05275242
10
56,0
58,85578
56,6002653
0,6002653
0,360318429
11
55,0
57,89183
56,4307189
1,43071895
2,046956712
12
53,0
56,66887
56,2616805
3,26168048
10,63855953
13
51,0
55,25166
56,0931484
5,09314836
25,94016022
14
50,5
54,06374
55,9251211
5,42512108
29,43193876
15
50,0
53,04781
55,7575971
5,75759713
33,14992472
16
50,0
52,28585
55,590575
5,590575
31,2545288
17
49,0
51,46439
55,4240532
6,42405318
41,26845926
18
48,0
50,59829
55,2580302
7,25803018
52,67900209
19
46,5
49,57372
55,0925045
8,5925045
73,83113361
20
45,0
48,43029
54,9274747
9,92747466
98,55475306
21
45,0
47,57272
54,7629392
9,76293916
95,31498103
22
45,0
46,92954
54,5988965
9,59889653
92,13881457
23
46,0
46,69715
54,4353453
8,43534529
71,15505014
24
47,0
46,77287
54,272284
7,27228397
52,8861141
25
48,5
47,20465
54,1097111
5,6097111
31,46885859
26
50,0
47,90349
53,9476252
3,94762521
15,58374483
27
51,0
48,67762
53,7860249
2,78602486
7,76193452
28
52,0
49,50821
53,6249086
1,62490858
2,640327895
29
53,0
50,38116
53,4642749
0,46427493
0,215551207
30
54,0
51,28587
53,3041224
0,69587755
0,484245565
31
54,5
52,0894
53,1444497
1,35555029
1,837516585
32
55,0
52,81705
52,9852553
2,01474473
4,059196314
33
57,0
53,86279
52,8265377
4,1734623
17,41778755
34
59,0
55,14709
52,6682956
6,33170443
40,09048097
35
60,5
56,48532
52,5105275
7,98947254
63,83167154
36
62,0
57,86399
52,3532319
9,64676807
93,06013412
37
64,0
59,39799
52,1964076
11,8035924
139,3247937
38
66,0
61,04849
52,040053
13,959947
194,8801197
39
66,5
62,41137
51,8841668
14,6158332
213,62258
40
67,0
63,55853
51,7287476
15,2712524
233,2111514
41
Прогнозн. значения
I полуг. 2010
51,5737939
42
II полуг. 2010
51,4193043
Средняя абсолютная ошибка
6,340121283
Среднеквадратическая ошибка
61,0
Значения ошибок довольно высоки, даже выше, чем при МНК.
Рассмотрим экспоненциальное сглаживание с коэффициентом адаптации =0,5:
t
Y
Y cглаж. при 0,5
Прогноз
|Y-Y*|
|Y-Y*|^2
1
75,0
65,3875
57,0467922
17,9532078
322,3176687
2
72,0
68,69375
56,9328127
15,0671873
227,0201338
3
69,0
68,84688
56,8190608
12,1809392
148,3752787
4
64,5
66,67344
56,7055363
7,79446372
60,75366462
5
60,0
63,33672
56,5922385
3,40776145
11,61283812
6
59,5
61,41836
56,4791672
3,02083282
9,125430933
7
59,0
60,20918
56,3663217
2,63367827
6,936261242
8
58,0
59,10459
56,2537017
1,74629826
3,049557607
9
57,0
58,05229
56,1413068
0,85869323
0,737354062
10
56,0
57,02615
56,0291364
0,02913636
0,000848928
11
55,0
56,01307
55,9171901
0,91719008
0,841237635
12
53,0
54,50654
55,8054675
2,80546746
7,870647644
13
51,0
52,75327
55,6939681
4,69396806
22,03333612
14
50,5
51,62663
55,5826914
5,08269143
25,83375222
15
50,0
50,81332
55,4716371
5,47163714
29,93881303
16
50,0
50,40666
55,3608047
5,36080474
28,73822744
17
49,0
49,70333
55,2501938
6,25019378
39,06492224
18
48,0
48,85166
55,1398038
7,13980382
50,97679853
19
46,5
47,67583
55,0296344
8,52963441
72,75466324
20
45,0
46,33792
54,9196851
9,91968513
98,40015311
21
45,0
45,66896
54,8099555
9,80995553
96,23522745
22
45,0
45,33448
54,7004452
9,70044516
94,09863636
23
46,0
45,66724
54,5911536
8,5911536
73,80792019
24
47,0
46,33362
54,4820804
7,4820804
55,98152716
25
48,5
47,41681
54,3732251
5,87322513
34,49477347
26
50,0
48,7084
54,2645874
4,26458736
18,18670533
27
51,0
49,8542
54,1561666
3,15616664
9,961387858
28
52,0
50,9271
54,0479625
2,04796255
4,194150592
29
53,0
51,96355
53,9399746
0,93997465
0,883552334
30
54,0
52,98178
53,8322025
0,1677975
0,028156
31
54,5
53,74089
53,7246457
0,77535431
0,601174303
32
55,0
54,37044
53,6173038
1,38269622
1,911848842
33
57,0
55,68522
53,5101763
3,48982367
12,17886922
34
59,0
57,34261
53,4032629
5,59673707
31,32346583
35
60,5
58,92131
53,2965631
7,20343686
51,8895026
36
62,0
60,46065
53,1900765
8,80992346
77,61475145
37
64,0
62,23033
53,0838027
10,9161973
119,1633637
38
66,0
64,11516
52,9777412
13,0222588
169,5792247
39
66,5
65,30758
52,8718916
13,6281084
185,725339
40
67,0
66,15379
52,7662535
14,2337465
202,5995401
41
Прогнозн. значения
I полуг. 2010
52,6608264
42
II полуг. 2010
52,55561
Средняя абсолютная ошибка
6,298872639
Среднеквадратическая ошибка
60,2
t
Y
Y cглаж.
Прогноз
|Y-Y*|
|Y-Y*|^2
1
75,0
70,19375
56,5903813
18,4096187
338,9140602
2
72,0
71,54844
56,5338192
15,4661808
239,202748
3
69,0
69,63711
56,4773137
12,5226863
156,8176733
4
64,5
65,78428
56,4208646
8,07913543
65,27242926
5
60,0
61,44607
56,3644719
3,63552809
13,2170645
6
59,5
59,98652
56,3081356
3,19186439
10,18799829
7
59,0
59,24663
56,2518556
2,74814438
7,55229754
8
58,0
58,31166
56,1956319
1,80436812
3,255744313
9
57,0
57,32791
56,1394643
0,86053566
0,740521628
10
56,0
56,33198
56,0833529
0,08335293
0,006947711
11
55,0
55,33299
56,0272976
1,02729761
1,055340383
12
53,0
53,58325
55,9712983
2,97129832
8,828613697
13
51,0
51,64581
55,915355
4,915355
24,16071474
14
50,5
50,78645
55,8594676
5,35946759
28,72389285
15
50,0
50,19661
55,803636
5,80363604
33,68219132
16
50,0
50,04915
55,7478603
5,7478603
33,03789802
17
49,0
49,26229
55,6921403
6,6921403
44,78474184
18
48,0
48,31557
55,636476
7,636476
58,3157657
19
46,5
46,95389
55,5808673
9,08086733
82,46215152
20
45,0
45,48847
55,5253142
10,5253142
110,78224
21
45,0
45,12212
55,4698167
10,4698167
109,6170614
22
45,0
45,03053
55,4143746
10,4143746
108,4591982
23
46,0
45,75763
55,3589879
9,35898792
87,59065485
24
47,0
46,68941
55,3036566
8,3036566
68,95071294
25
48,5
48,04735
55,2483806
6,74838059
45,54064054
26
50,0
49,51184
55,1931598
5,19315982
26,96890893
27
51,0
50,62796
55,1379942
4,13799425
17,1229964
28
52,0
51,65699
55,0828838
3,08288381
9,504172612
29
53,0
52,66425
55,0278285
2,02782846
4,112088274
30
54,0
53,66606
54,9728281
0,97282814
0,946394588
31
54,5
54,29152
54,9178828
0,41788279
0,174626025
32
55,0
54,82288
54,8629924
0,13700764
0,018771095
33
57,0
56,45572
54,8081568
2,19184321
4,804176679
34
59,0
58,36393
54,753376
4,24662398
18,0338152
35
60,5
59,96598
54,69865
5,80134999
33,65566165
36
62,0
61,4915
54,6439787
7,3560213
54,11104929
37
64,0
63,37287
54,589362
9,41063796
88,56010683
38
66,0
65,34322
54,5348
11,4652
131,4508119
39
66,5
66,2108
54,4802924
12,0197076
144,4733703
40
67,0
66,8027
54,4258394
12,5741606
158,1095158
41
Прогнозн. значения
I полуг. 2010
54,3714407
42
II полуг. 2010
54,3170965
Средняя абсолютная ошибка
6,322286839
Среднеквадратическая ошибка
59,3
4.2 Двухпараметрическая модель Хольта
Xt=a1,t+ξt,
Xt-значение временного ряда в точке t,
A1,t-коэффициент , т.е. уровень ряда, который изменяется во времени,
ξt-случайные неавтокоррелированные отклонения с M=0 и D=const.
Формулы для расчета:
xˉr(t)=aˉ1,t+aˉ2,t*r
aˉ1,t=α1*xt+(1- α1)*(aˉ1,t-1+aˉ2,t-1)
aˉ2,t= α2 *( aˉ1,t- aˉ1,t-1)+(1- α2)aˉ2,t-1
0< α1<1, 0< α2<1.
Результаты проведенных вычислений:
t
Y
Y1(t)
α1,t
α2,t
|Y-Y1(t)|
|Y-Y1(t)|^2
I полуг. 1990
1
75,0
117,5451
58,83015
58,71499
42,54514
1810,089
II полуг. 1990
2
72,0
167,6065
112,9906
54,61592
95,60654
9140,611
I полуг. 1991
3
69,0
203,4872
157,7459
45,74133
134,4872
18086,81
II полуг. 1991
4
64,5
222,821
189,5885
33,23248
158,321
25065,53
I полуг. 1992
5
60,0
225,1175
206,5389
18,5786
165,1175
27263,78
II полуг. 1992
6
59,5
212,2288
208,5557
3,673022
152,7288
23326,07
I полуг. 1993
7
59,0
186,7883
196,9059
-10,1176
127,7883
16329,85
II полуг. 1993
8
58,0
152,201
173,9095
-21,7085
94,20097
8873,822
I полуг. 1994
9
57,0
112,4043
142,6809
-30,2766
55,40427
3069,633
II полуг. 1994
10
56,0
71,41086
106,7638
-35,353
15,41086
237,4945
I полуг. 1995
11
55,0
32,93981
69,76977
-36,83
22,06019
486,6521
II полуг. 1995
12
53,0
-0,07872
34,94583
-35,0245
53,07872
2817,35
I полуг. 1996
13
51,0
-25,3983
5,029153
-30,4275
76,39831
5836,701
II полуг. 1996
14
50,5
-41,4051
-17,8085
-23,5966
91,90509
8446,546
I полуг. 1997
15
50,0
-47,6347
-32,2646
-15,3702
97,63474
9532,542
II полуг. 1997
16
50,0
-44,4543
-37,8713
-6,58303
94,45429
8921,613
I полуг. 1998
17
49,0
-33,281
-35,1089
1,827857
82,28101
6770,164
II полуг. 1998
18
48,0
-16,0098
-25,1529
9,143148
64,00976
4097,249
I полуг. 1999
19
46,5
5,010245
-9,75878
14,76903
41,48976
1721,4
II полуг. 1999
20
45,0
27,37732
9,00922
18,3681
17,62268
310,5587
I полуг. 2000
21
45,0
49,09374
29,13959
19,95414
4,093736
16,75868
II полуг. 2000
22
45,0
68,27007
48,68436
19,58571
23,27007
541,4962
I полуг. 2001
23
46,0
83,62447
66,04306
17,5814
37,62447
1415,6
II полуг. 2001
24
47,0
94,24722
79,96202
14,2852
47,24722
2232,3
I полуг. 2002
25
48,5
99,84045
89,6725
10,16795
51,34045
2635,842
II полуг. 2002
26
50,0
100,5387
94,8564
5,68231
50,53871
2554,162
I полуг. 2003
27
51,0
96,80867
95,58484
1,223826
45,80867
2098,434
II полуг. 2003
28
52,0
89,51885
92,3278
-2,80895
37,51885
1407,664
I полуг. 2004
29
53,0
79,77131
85,86696
-6,09565
26,77131
716,7031
II полуг. 2004
30
54,0
68,77911
77,19418
-8,41507
14,77911
218,4221
I полуг. 2005
31
54,5
57,65101
67,3512
-9,70019
3,151012
9,928877
II полуг. 2005
32
55,0
47,44713
57,38591
-9,93878
7,552869
57,04583
I полуг. 2006
33
57,0
39,3234
48,40242
-9,07902
17,6766
312,4623
II полуг. 2006
34
59,0
33,98293
41,29106
-7,30813
25,01707
625,8538
I полуг. 2007
35
60,5
31,71305
36,63464
-4,92159
28,78695
828,6887
II полуг. 2007
36
62,0
32,54598
34,74174
-2,19576
29,45402
867,5395
I полуг. 2008
37
64,0
36,32648
35,69138
0,635097
27,67352
765,8239
II полуг. 2008
38
66,0
42,59954
39,29383
3,305714
23,40046
547,5814
I полуг. 2009
39
66,5
50,44634
44,98959
5,456755
16,05366
257,7199
II полуг. 2009
40
67,0
59,04829
52,10171
6,946585
7,951706
63,22963
Прогнозн. значения
I полуг. ‘10
96,2064
II полуг. ‘10
105,3756
alfa1=
0,1
alfa2=
0,9
Средняя абс. ошибка
55,20639
a1t
-0,0645
Среднеквадр. ошибка
5007,9
a2t
57,098
t
Y
Y1(t)
a1,t
a2,t
|Y-Y1(t)|
|Y-Y1(t)|^2
I полуг. 1990
1
75,0
127,6064
66,01675
61,58963
52,60638
2767,431
II полуг. 1990
2
72,0
147,4912
99,80319
47,68803
75,49122
5698,924
I полуг. 1991
3
69,0
136,3108
108,2456
28,06523
67,31084
4530,749
II полуг. 1991
4
64,5
110,5179
100,4054
10,11252
46,01794
2117,65
I полуг. 1992
5
60,0
82,742
85,25897
-2,51697
22,742
517,1986
II полуг. 1992
6
59,5
62,79353
71,121
-8,32747
3,293534
10,84737
I полуг. 1993
7
59,0
51,62092
60,89677
-9,27585
7,379083
54,45087
II полуг. 1993
8
58,0
47,12938
54,81046
-7,68108
10,87062
118,1704
I полуг. 1994
9
57,0
46,85127
52,06469
-5,21342
10,14873
102,9968
II полуг. 1994
10
56,0
48,49939
51,42563
-2,92624
7,500608
56,25912
I полуг. 1995
11
55,0
50,44861
51,7497
-1,30109
4,551392
20,71517
II полуг. 1995
12
53,0
51,06106
51,7243
-0,66324
1,938937
3,759475
I полуг. 1996
13
51,0
50,35203
51,03053
-0,67851
0,647975
0,419871
II полуг. 1996
14
50,5
49,7845
50,42601
-0,64151
0,7155
0,51194
I полуг. 1997
15
50,0
49,30461
49,89225
-0,58764
0,695388
0,483564
II полуг. 1997
16
50,0
49,23852
49,65231
-0,41379
0,761485
0,579859
I полуг. 1998
17
49,0
48,64584
49,11926
-0,47342
0,354162
0,125431
II полуг. 1998
18
48,0
47,68804
48,32292
-0,63488
0,31196
0,097319
I полуг. 1999
19
46,5
46,16213
47,09402
-0,93189
0,337869
0,114156
II полуг. 1999
20
45,0
44,35864
45,58107
-1,22242
0,641356
0,411338
I полуг. 2000
21
45,0
43,61724
44,67932
-1,06208
1,382761
1,912028
II полуг. 2000
22
45,0
43,59223
44,30862
-0,71639
1,407773
1,981825
I полуг. 2001
23
46,0
44,68166
44,79611
-0,11445
1,318336
1,738009
II полуг. 2001
24
47,0
46,30597
45,84083
0,465135
0,694033
0,481682
I полуг. 2002
25
48,5
48,41663
47,40298
1,013643
0,083374
0,006951
II полуг. 2002
26
50,0
50,6178
49,20831
1,409486
0,6178
0,381676
I полуг. 2003
27
51,0
52,31394
50,8089
1,505036
1,313936
1,726429
II полуг. 2003
28
52,0
53,58352
52,15697
1,426552
1,583521
2,507537
I полуг. 2004
29
53,0
54,57243
53,29176
1,280672
1,572433
2,472544
II полуг. 2004
30
54,0
55,42378
54,28622
1,137564
1,42378
2,027151
I полуг. 2005
31
54,5
55,86851
54,96189
0,906619
1,368509
1,872818
II полуг. 2005
32
55,0
56,12375
55,43425
0,689492
1,123746
1,262806
I полуг. 2006
33
57,0
57,47043
56,56187
0,908555
0,470428
0,221303
II полуг. 2006
34
59,0
59,52616
58,23521
1,290948
0,526162
0,276847
I полуг. 2007
35
60,5
61,54749
60,01308
1,534408
1,047489
1,097232
II полуг. 2007
36
62,0
63,42128
61,77374
1,647535
1,42128
2,020036
I полуг. 2008
37
64,0
65,50286
63,71064
1,792215
1,502855
2,258574
II полуг. 2008
38
66,0
67,66793
65,75143
1,916502
1,667929
2,781988
I полуг. 2009
39
66,5
68,70848
67,08396
1,624519
2,208484
4,877401
II полуг. 2009
40
67,0
69,05164
67,85424
1,197398
2,05164
4,209228
Прогнозн. значения
I полуг. 10
89,4224
II полуг. 10
95,1104
alfa1=
0,5
alfa2=
0,5
Средняя абс. ошибка
8,477581
a1t
-0,0645
Среднеквадр. ошибка
401,0
a2t
57,098
t
Y
Y1(t)
a1,t
a2,t
|Y-Y1(t)|
|Y-Y1(t)|^2
I полуг. 1990
1
75,0
131,3793
71,4067
59,97264
56,37934
3178,63
II полуг. 1990
2
72,0
134,3478
83,87587
50,47195
62,34781
3887,25
I полуг. 1991
3
69,0
122,0859
82,06956
40,0163
53,08586
2818,108
II полуг. 1991
4
64,5
106,8197
76,01717
30,80256
42,31973
1790,96
I полуг. 1992
5
60,0
92,67535
69,36395
23,3114
32,67535
1067,678
II полуг. 1992
6
59,5
84,13842
66,13507
18,00335
24,63842
607,0515
I полуг. 1993
7
59,0
78,00888
64,02768
13,9812
19,00888
361,3376
II полуг. 1993
8
58,0
72,78155
62,00178
10,77978
14,78155
218,4944
I полуг. 1994
9
57,0
68,41104
60,15631
8,254729
11,41104
130,2118
II полуг. 1994
10
56,0
64,75117
58,48221
6,268963
8,751171
76,58299
I полуг. 1995
11
55,0
61,65901
56,95023
4,708776
6,65901
44,34241
II полуг. 1995
12
53,0
58,05514
54,7318
3,323334
5,055136
25,5544
I полуг. 1996
13
51,0
54,60554
52,41103
2,194512
3,605539
12,99991
II полуг. 1996
14
50,5
52,85873
51,32111
1,537626
2,358734
5,563625
I полуг. 1997
15
50,0
51,65198
50,57175
1,080229
1,651975
2,729022
II полуг. 1997
16
50,0
51,14631
50,3304
0,815912
1,146308
1,314021
I полуг. 1998
17
49,0
49,90176
49,42926
0,472503
0,901765
0,81318
II полуг. 1998
18
48,0
48,54857
48,38035
0,168221
0,548574
0,300933
I полуг. 1999
19
46,5
46,75016
46,90971
-0,15955
0,250164
0,062582
II полуг. 1999
20
45,0
44,91046
45,35003
-0,43958
0,089544
0,008018
I полуг. 2000
21
45,0
44,55684
44,98209
-0,42525
0,443159
0,19639
II полуг. 2000
22
45,0
44,55702
44,91137
-0,35434
0,442976
0,196228
I полуг. 2001
23
46,0
45,58794
45,7114
-0,12347
0,412064
0,169796
II полуг. 2001
24
47,0
46,82005
46,71759
0,102462
0,179951
0,032382
I полуг. 2002
25
48,5
48,53526
48,16401
0,371254
0,035264
0,001244
II полуг. 2002
26
50,0
50,31266
49,70705
0,605612
0,312665
0,097759
I полуг. 2003
27
51,0
51,57812
50,86253
0,715585
0,578118
0,334221
II полуг. 2003
28
52,0
52,69871
51,91562
0,783086
0,69871
0,488196
I полуг. 2004
29
53,0
53,77103
52,93974
0,831293
0,771035
0,594495
II полуг. 2004
30
54,0
54,82213
53,95421
0,867927
0,822134
0,675905
I полуг. 2005
31
54,5
55,38081
54,56443
0,816386
0,880813
0,775831
II полуг. 2005
32
55,0
55,83162
55,07616
0,755456
0,831618
0,691589
I полуг. 2006
33
57,0
57,70872
56,76632
0,942397
0,708721
0,502285
II полуг. 2006
34
59,0
59,89075
58,74174
1,149002
0,890746
0,793428
I полуг. 2007
35
60,5
61,62463
60,37815
1,246482
1,124631
1,264796
II полуг. 2007
36
62,0
63,23147
61,92493
1,306541
1,231468
1,516512
I полуг. 2008
37
64,0
65,2758
63,84629
1,429506
1,2758
1,627665
II полуг. 2008
38
66,0
67,40054
65,85516
1,545378
1,400538
1,961508
I полуг. 2009
39
66,5
68,0814
66,68011
1,401292
1,5814
2,500826
II полуг. 2009
40
67,0
68,44455
67,21628
1,228268
1,444548
2,08672
Прогнозн. значения
I полуг. 10
48,157
II полуг. 10
47,857
alfa1=
0,8
alfa2=
0,2
Средняя абс. ошибка
9,093306
a1t
-0,0645
Среднеквадр. ошибка
356,2
a2t
57,098
При сравнении результатов лучшей оказалась модель с параметрами адаптации 1=0,5 и 2=0,5 (средняя абсолютная и среднеквадратическая ошибки приняли наименьшие значения).
4.3 Трехпараметрическая модель Бокса и Дженкинса
Эта модель получена из модели Хольта путем включения разности ошибок et-et-1.
Модель:
xˉr(t)=aˉ1,t+aˉ2,t*r
Расчетные формулы:
aˉ1,t=α1*xt+(1- α1)*(aˉ1,t-1+aˉ2,t-1)+ α3*(et-et-1)
aˉ2,t= α2 *( aˉ1,t- aˉ1,t-1)+(1- α2)aˉ2,t-1
et=xt-xˉt 0<α1<1, 0<α2<1, 0<α3<1
Результаты вычислений:
t
Y
Y1(t)
a1,t
a2,t
|Y-Y1(t)|
|Y-Y1(t)|^2
I полуг. 1990
1
75,0
138,1449
77,044634
61,1002268
63,14486
3987,273
II полуг. 1990
2
72,0
116,9955
69,60354736
47,39196411
44,99551
2024,596
I полуг. 1991
3
69,0
102,8095
65,68050445
37,12896271
33,80947
1143,08
II полуг. 1991
4
64,5
90,88317
61,93008716
28,95308671
26,38317
696,0719
I полуг. 1992
5
60,0
80,90717
58,44226176
22,46490429
20,90717
437,1096
II полуг. 1992
6
59,5
76,12708
58,20300679
17,92407244
16,62708
276,4598
I полуг. 1993
7
59,0
72,35115
58,04374671
14,30740593
13,35115
178,2533
II полуг. 1993
8
58,0
68,69794
57,38396722
11,31396885
10,69794
114,4458
I полуг. 1994
9
57,0
65,57796
56,66964857
8,908311348
8,57796
73,5814
II полуг. 1994
10
56,0
62,92158
55,94071307
6,980861978
6,921575
47,9082
I полуг. 1995
11
55,0
60,63353
55,19748388
5,436043744
5,633528
31,73663
II полуг. 1995
12
53,0
57,68491
53,64631262
4,038600743
4,684913
21,94841
I полуг. 1996
13
51,0
54,97571
52,06174035
2,913966141
3,975706
15,80624
II полуг. 1996
14
50,5
53,93725
51,68201944
2,255228731
3,437248
11,81467
I полуг. 1997
15
50,0
53,07101
51,33602415
1,734983926
3,071008
9,431091
II полуг. 1997
16
50,0
52,74814
51,35613322
1,392008956
2,748142
7,552285
I полуг. 1998
17
49,0
51,54108
50,58224572
0,958829665
2,541075
6,457064
II полуг. 1998
18
48,0
50,37627
49,77138091
0,604890769
2,376272
5,646667
I полуг. 1999
19
46,5
48,82187
48,576859
0,245008233
2,321867
5,391067
II полуг. 1999
20
45,0
47,3494
47,39063805
-0,041237604
2,3494
5,519682
I полуг. 2000
21
45,0
47,41936
47,44206145
-0,022705401
2,419356
5,853284
II полуг. 2000
22
45,0
47,38144
47,40668175
-0,025240262
2,381441
5,671264
I полуг. 2001
23
46,0
48,3428
48,20360873
0,139193186
2,342802
5,488721
II полуг. 2001
24
47,0
49,25082
48,98348873
0,267330549
2,250819
5,066187
I полуг. 2002
25
48,5
50,64784
50,19223128
0,45561295
2,147844
4,613235
II полуг. 2002
26
50,0
52,04737
51,43444007
0,612932118
2,047372
4,191733
I полуг. 2003
27
51,0
52,88335
52,23324538
0,650106756
1,883352
3,547015
II полуг. 2003
28
52,0
53,69595
53,01875918
0,677188165
1,695947
2,876237
I полуг. 2004
29
53,0
54,51472
53,81393247
0,70078519
1,514718
2,29437
II полуг. 2004
30
54,0
55,33201
54,61180994
0,720203645
1,332014
1,77426
I полуг. 2005
31
54,5
55,66888
55,01256784
0,656314496
1,168882
1,366286
II полуг. 2005
32
55,0
56,00467
55,40178057
0,602894142
1,004675
1,009371
I полуг. 2006
33
57,0
57,79525
56,99441022
0,800841245
0,795251
0,632425
II полуг. 2006
34
59,0
59,59167
58,62490252
0,966771455
0,591674
0,350078
I полуг. 2007
35
60,5
60,84454
59,83008857
1,014454375
0,344543
0,11871
II полуг. 2007
36
62,0
62,06641
61,01738361
1,049022508
0,066406
0,00441
I полуг. 2008
37
64,0
63,7691
62,61113324
1,157967933
0,230899
0,053314
II полуг. 2008
38
66,0
65,46716
64,21917385
1,247982467
0,532844
0,283922
I полуг. 2009
39
66,5
65,70429
64,62478615
1,079508435
0,795705
0,633147
II полуг. 2009
40
67,0
65,93027
64,99301483
0,937252483
1,069733
1,144328
Прогнозн. значения
I полуг. 2010
46,03716
II полуг. 2010
45,60244
alfa1=
0,8
alfa2=
0,2
Средняя абсолютная ошибка
7,629283
alfa3=
0,1
Среднеквадратичская ошибка
228,7
a1t
-0,0645
a2t
57,098
t
Y
Y1(t)
a1,t
a2,t
|Y-Y1(t)|
|Y-Y1(t)|^2
I полуг. 1990
1
75,0
188,1117
96,133902
91,9778412
113,1117
12794,27
II полуг. 1990
2
72,0
124,2434
79,21064208
45,03274877
52,24339
2729,372
I полуг. 1991
3
69,0
96,03969
72,84151336
23,19817203
27,03969
731,1446
II полуг. 1991
4
64,5
81,71841
69,69026148
12,02815209
17,21841
296,4738
I полуг. 1992
5
60,0
73,12559
67,32678527
5,798805526
13,12559
172,2811
II полуг. 1992
6
59,5
71,09764
67,50902038
3,588624384
11,59764
134,5054
I полуг. 1993
7
59,0
70,33775
67,93124014
2,406506487
11,33775
128,5445
II полуг. 1993
8
58,0
69,0882
67,75190167
1,33630081
11,0882
122,9482
I полуг. 1994
9
57,0
68,00495
67,40894571
0,596006909
11,00495
121,109
II полуг. 1994
10
56,0
67,14766
67,02213921
0,125520242
11,14766
124,2703
I полуг. 1995
11
55,0
66,40995
66,59245163
-0,1825004
11,40995
130,187
II полуг. 1995
12
53,0
64,79733
65,53893786
-0,741608505
11,79733
139,177
I полуг. 1996
13
51,0
63,24803
64,38522104
-1,13719519
12,24803
150,0141
II полуг. 1996
14
50,5
63,32024
64,14605831
-0,825814752
12,82024
164,3586
I полуг. 1997
15
50,0
63,42979
64,00807244
-0,578280377
13,42979
180,3593
II полуг. 1997
16
50,0
63,75763
64,06839967
-0,310771885
13,75763
189,2723
I полуг. 1998
17
49,0
63,04728
63,54673717
-0,499460632
14,04728
197,326
II полуг. 1998
18
48,0
62,23491
62,91414272
-0,679233048
14,23491
202,6327
I полуг. 1999
19
46,5
61,0929
62,030577
-0,937679264
14,5929
212,9527
II полуг. 1999
20
45,0
60,09411
61,17191414
-1,077805271
15,09411
227,8321
I полуг. 2000
21
45,0
60,77206
61,32618436
-0,55412103
15,77206
248,758
II полуг. 2000
22
45,0
60,82389
61,22004525
-0,396156089
15,82389
250,3955
I полуг. 2001
23
46,0
61,9276
61,81082618
0,116774909
15,9276
253,6885
II полуг. 2001
24
47,0
62,74432
62,35046618
0,393848944
15,74432
247,8835
I полуг. 2002
25
48,5
64,06874
63,27669385
0,792045968
15,56874
242,3857
II полуг. 2002
26
50,0
65,39452
64,30332022
1,091203403
15,39452
236,9914
I полуг. 2003
27
51,0
65,91231
64,89973615
1,012571598
14,91231
222,3769
II полуг. 2003
28
52,0
66,39775
65,45627755
0,9414678
14,39775
207,2951
I полуг. 2004
29
53,0
66,95799
66,04179742
0,916192603
13,95799
194,8255
II полуг. 2004
30
54,0
67,54132
66,63542981
0,905894994
13,54132
183,3675
I полуг. 2005
31
54,5
67,6626
66,93770352
0,724901221
13,1626
173,2542
II полуг. 2005
32
55,0
67,80087
67,2053417
0,59552364
12,80087
163,8622
I полуг. 2006
33
57,0
69,44728
68,38323066
1,064047563
12,44728
154,9347
II полуг. 2006
34
59,0
71,08802
69,67470755
1,41331467
12,08802
146,1203
I полуг. 2007
35
60,5
71,98759
70,59026572
1,397323704
11,48759
131,9647
II полуг. 2007
36
62,0
72,80768
71,45215084
1,355525294
10,80768
116,8059
I полуг. 2008
37
64,0
74,15546
72,63339973
1,52206451
10,15546
103,1335
II полуг. 2008
38
66,0
75,50523
73,85752155
1,647711799
9,505233
90,34946
I полуг. 2009
39
66,5
75,35309
74,17435846
1,17872923
8,853088
78,37716
II полуг. 2009
40
67,0
75,20909
74,37904449
0,830049155
8,209094
67,38922
Прогнозн. значения
I полуг. 2010
92,1107
II полуг. 2010
96,2876
alfa1=
0,6
alfa2=
0,6
Средняя абсолютная ошибка
16,82262
alfa3=
0,3
Среднеквадратичская ошибка
566,6
a1t
-0,0645
a2t
57,098
5 Выбор лучшей модели
Представим все рассмотренные модели в виде таблицы, содержащей среднюю абсолютную и среднеквадратическую ошибки.
Модель
Cредняя абсолютная ошибка
Среднеквадратическая ошибка
Коэффициент детерминации
Линейная модель
6,35
59,3
0,93%
Полиномиальная модель
1,14
2
96,61%
Экспоненциальная модель
6,3
59,6
0,7%
Экспоненциальное сглаживание (=0,25)
6,34
61
27%
Двухпараметрическая модель Хольта (=1, 1=0,5, 2=0,5)
8,48
401
69%
Трехпараметрическая модель Бокса и Дженкинса (=1, 1=0,8, 2=0,2, 3=0,1)
7,63
228,7
53%
Лучшей является полиномиальная модель МНК. Её и проверим на адекватность. Для проверки воспользуемся ППП Statistica. Импортируем данные в программу, предварительно преобразовав их. Нам необходимо привести модель к линейному виду, т.к. для проверки адекватности модель должна быть линейной. Для этого прологарифмируем обе части уравнения 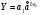 . Получим: ln y=ln a1+a2*ln x. В нашем случае уравнение модели записывается в следующем виде: у=1195,7*е0,0154*х. Произведение а2*ln x можно представить в виде временного ряда, т.к. значения х нам известны и для упрощения расчетов. Тогда в ППП Statistica импортируем в качестве первого параметра – ВР, полученный умножением х на 0,0154, а в качестве второго параметра – логарифмированный ряд исходных значений у.
. Получим: ln y=ln a1+a2*ln x. В нашем случае уравнение модели записывается в следующем виде: у=1195,7*е0,0154*х. Произведение а2*ln x можно представить в виде временного ряда, т.к. значения х нам известны и для упрощения расчетов. Тогда в ППП Statistica импортируем в качестве первого параметра – ВР, полученный умножением х на 0,0154, а в качестве второго параметра – логарифмированный ряд исходных значений у.
Для проверки гипотезы об адекватности модели в целом используется F-статистика (статистика Фишера). Для того, чтобы принять гипотезу об адекватности модели, необходимо, чтобы этот показатель был достаточно высок, а соответствующая ей вероятность р как можно ниже. У нас F=238,82, а р=0,0000, что показывает высокую достоверность данных. Множественная регрессия высоко значима.
Далее можно определить значимость (адекватность) коэффициентов в модели.
Для оценки значимости коэффициентов рассматривается показатель р – level. Значения этого показателя равны нулю и для свободного члена, и для переменной х (Var 1), следовательно, нулевую гипотезу о незначимости коэффициентов можно отвергнуть.
Остатки – это разность между исходными (наблюдаемыми) значениями зависимой переменной и предсказанными значениями. Исследование остатков также показывают степень адекват ности модели. По основному предположению МНК в остатках должна отсутствовать автокорреляция.
Получили d=1,96751, что говорит об адекватности нашей модели.
Заключение
В данной курсовой работе рассматривались данные по полугодиям за 20 лет и осуществлялся прогноз на момент времени t=41 и 42, что соответствовало I и II полугодиям 2010 года. Были построены следующие модели прогнозирования потребления мясопродукции на человека:
- с использованием метода наименьших квадратов (линейная, экспоненциальная и полиномиальная, Excel),
- экспоненциальное сглаживание (Excel),
- модель Хольта (Excel),
-модель Бокса и Дженкинса (Excel).
Выбранные модели дают довольно различные результаты, и лучшие результаты были получены при использовании полиномиальной модели метода наименьших квадратов и модели Хольта. Результаты вычислений представлены в таблицах. Рассчитана абсолютная ошибка прогноза и средняя относительная ошибка прогноза, статистика Дарбина-Уотсона. Именно эти показатели рассматривались в качестве критерия для выбора модели, дающей наилучшее прогнозное значение интересующей нас переменной, т.е. общего числа страховых организаций.
Список использованных источников
1. Бабкова Е.В. и др. «Методы прогнозирования показателей развития сложных систем», Уфа 2005.
2. Боровиков В.П., Ивченко Г.И. Прогнозирование в системе STATISTICA в среде Windows. - М. : Финансы и статистика : 2000. – 384 с.
3. www.gks.ru – Росстат.

Нравится материал? Поддержи автора!
Ещё документы из категории разное:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ