Синтез системы автоматического регулирования массы квадратного метра бумажного полотна

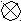
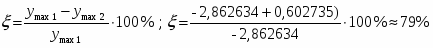
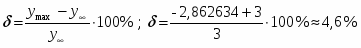
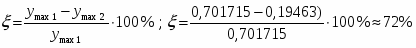
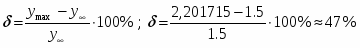
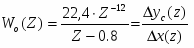
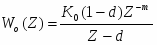
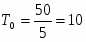
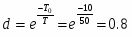
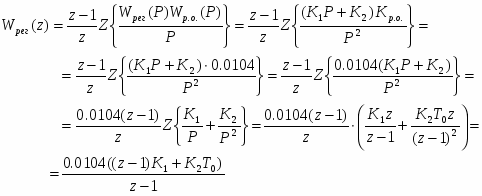
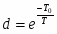
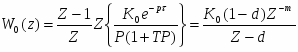
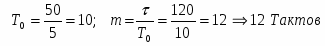
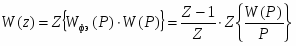
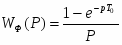
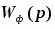
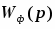
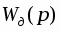
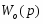
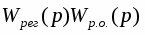
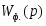
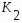
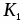
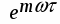
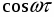
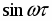
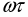
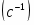
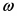
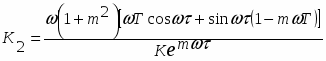
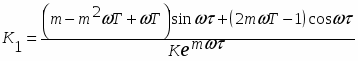
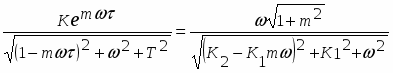
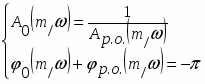
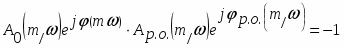
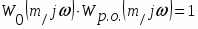
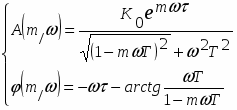
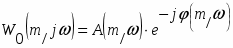
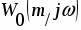
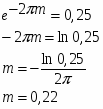
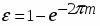
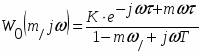
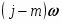
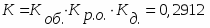
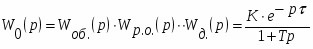
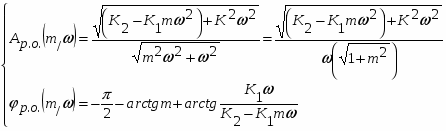
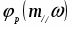
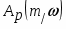
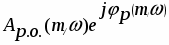
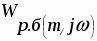
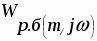
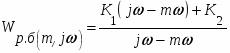
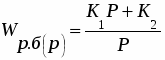
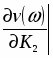
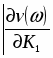
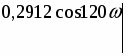
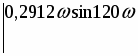
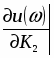
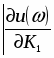
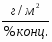
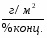
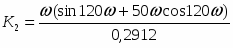
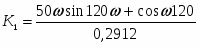
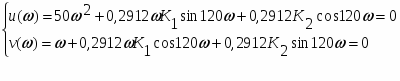
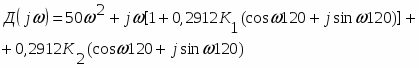
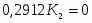
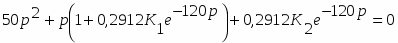
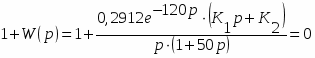
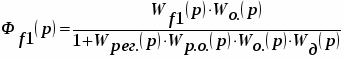
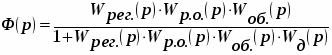
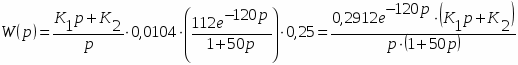
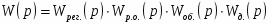
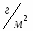
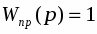
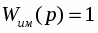
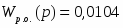
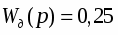
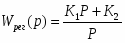
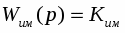
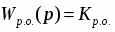
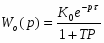
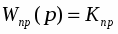
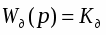
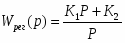
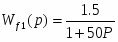
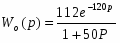
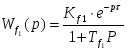
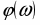
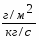
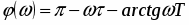
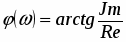
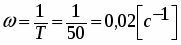
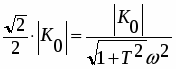
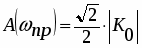
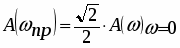
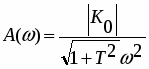
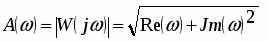
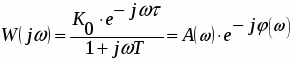
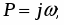
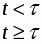
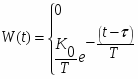
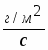
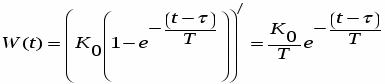
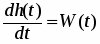
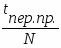
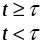
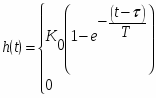
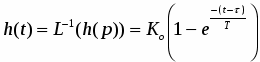
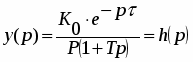
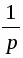
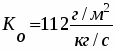
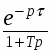
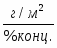
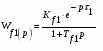
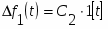
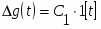
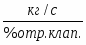
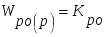
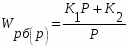
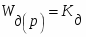
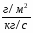
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

Кафедра АХТП

КУРСОВАЯ РАБОТА

по

ТЕОРИИ УПРАВЛЕНИЯ

«СИНТЕЗ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ МАССЫ КВАДРАТНОГО МЕТРА БУМАЖНОГО ПОЛОТНА

ПО ЗАДАННЫМ КРИТЕРИЯМ КАЧЕСТВА»

Выполнил: студент V курса .

Ситников С. А. .

шифр 965-450 .

Проверил: преподаватель .

Селянинова Л. Н. .

С.-ПЕТЕРБУРГ

2000г.

№

Наименование элементов схемы АСР, их математическая модель, параметры модели. Рассматриваемые воздействия. Требования к проектируемой системе регулирования.

Обозначения переменных.

Размерность переменных

Значение

Объект регулирования. Канал: “изменение расхода массы - изменение массы 1 м² полотна”. Математическая модель объекта:

W_об(р)= К₀

Параметры модели:

постоянная времени объекта
коэффициент передачи объекта
запаздывание по рассматриваемому каналу передачи информации

К₀



112

120

Измерительное устройство, датчик электронный с преобразователем.

Математическая модель датчика:

Параметр модели: коэффициент передачи

К_д

0,25

Регулирующий блок /совокупность электронного регулятора и электродвигателя/ приближенно реализует ПИ-закон регулирования.

Математическая модель регулирующего блока:

К₁ - пропорциональная составляющая закона регулирования

К₂ - интегральная составляющая закона регулирования

К₁

К₂

Регулирующий орган: клапан

Модель клапана:

Параметры модели: коэффициент передачи

К_ро

0,0104

Требования к качеству работы проектируемой системы:

Точность регулирования массы 1 м² полотна
Минимальное значение степени затухания





г/м²

0,4

0,75

Типовые входные воздействия:

Изменение задающего воздействия:

2. Изменение концентрированной массы:

С₁

С₂

г/м²

% конц.

1,5

-3

Канал передачи возмущения:

“Изменение концентрации массы” – “изменение массы 1 м² полотна” :

К_f₁

Т_f₁

1,1

Задача

Цель создания автоматической системы – достичь того, чтобы значение массы 1 кв. м. бумажного полотна было равно заданному. При этом требуется, чтобы точность регулирования, т.е. возможное отклонение, находилось в определенных пределах. Поэтому, для синтеза системы выбран принцип управления по отклонению регулируемой величины от задания.

Принцип работы

Объект регулирования – напорный ящик БДМ.

Регулируемая величина – масса 1 кв.м. полотна.

Регулирующая величина – расход массы.

Возмущающее воздействие – изменение концентрации массы.

Автоматический регулятор – средство решения задачи регулирования.

Автоматический регулятор состоит из электронного датчика измеряющего массу 1 кв.м. полотна, регулирующего блока (электрорегулятор и электродвигатель), приблизительно соответствующего ПИ-закону регулирования, клапана, изменяющего расход бумажной массы.

- бак массы
– напорный ящик
– сушильные группы
– каландр
– датчик массы 1кв.м. полотна
– преобразователь
– регулятор
– эл. двигатель - исполнительный механизм
– регулирующий орган - клапан

зад.

уст-во

сравн.

уст-во

Регулятор

Исп.

механ

Датчик

Рег.

орган

БДМ

Функциональная схема системы.

Текущее значение массы 1 кв.м. полотна фиксируется датчиком. Через преобразователь на регулирующий блок подается электрический сигнал. В регулирующем блоке происходит сравнение поступившего сигнала с заданным значением. В результате сравнения полученное отклонение определяет величину управляющего воздействия, которое должно нейтрализовать отклонение. В зависимости от величины и знака управляющего воздействия, управляющий блок формирует воздействие на исполнительный механизм (эл. двигатель).

Модель системы управления в виде «черного ящика»

О.Р.

Δg(t)

Δf(t)

Δy(t)

Δg(t) [кг/м³] – изменение расхода бумажной массы (задающее воздействие)

Δf(t) [%] - изменение концентрации массы (возмущающее воздействие)

Δy(t) [г/м²] – изменение массы 1кв.м. полотна (выходная переменная)

Временные характеристики по каналу управления.

Передаточная функция объекта регулирования.

W_об(р)= К₀

коэффициент передачи
постоянная времени Т =50 с

запаздывание информации  =120 с

Это апериодическое звено 1-го порядка с запаздыванием.

Переходная функция h(t) определяется как переходной процесс на выходе звена при подаче на его вход единичного ступенчатого воздействия 1[t] при нулевых начальных условиях. Чтобы получить переходную функцию звена, нужно изменить его входной сигнал на одну единицу. (расход массы на 1кг/с).

W_(p)

X Y

х(t)=1[t]

Зная,

x (p)= x L [1(t)]=

Получаем изображение переходной функции:

Обратное преобразование дает переходную функцию звена первого порядка с запаздыванием:

; % влажности

;

Для расчета переходной функции необходимо приблизительно оценить время окончания переходного процесса. Его можно вычислить по выражению:

t_пер.пр.  3 - 4T+  320 c

Выбираем шаг расчета:

t = , N – желаемое количество точек графика;

N=10,

t = 32 c

Результаты расчета сведены в Таблицу 1.

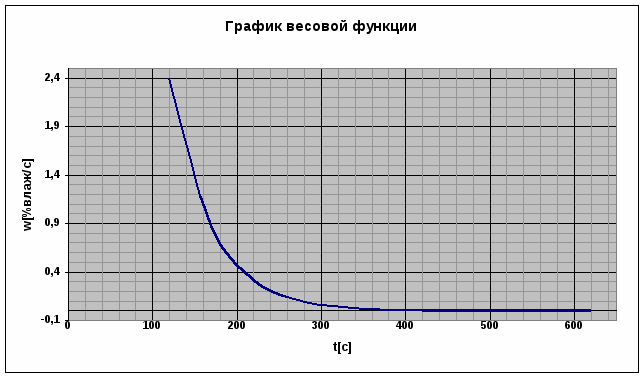
Весовая функция W(t) представляет собой переходной процесс на выходе звена на единичную импульсную функцию  [t] при нулевых начальных условиях. Единичная импульсная функция является производной от единичной ступенчатой функции  [t] =1 [t]. Переходная весовая функции связаны соотношением:

Отсюда:

, , т.е.

;

Таблица 1.

Расчет переходной и весовой функции объекта по каналу управления.

T, c

120

152

184

216

248

280

312

344

376

408

440

H(t),г/м

0,0

52,943

80,860

95,580

103,34

107,43

109,593

110,731

111,331

111,647

111,81

W(t),г/м

0,0

2,4

1,266

0,667

0,352

0,186

0,098

0,052

0,027

0,014

0,008

0,004

По данным Таблицы 1 построены графики переходной и весовой функции.

Основные параметры объекта по каналу управления могут быть определены из этих графиков.



Т

К₀



Т

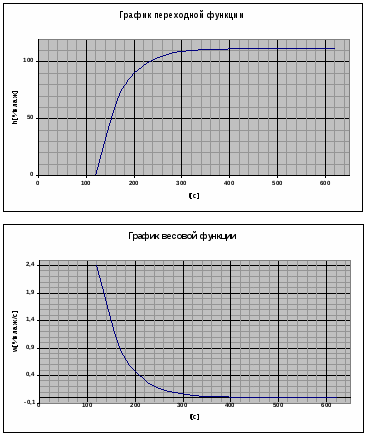
Основные параметры объекта по каналу управления могут быть

Частотные характеристики объекта по каналу управления.

Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе.

Выражения частотных характеристик по каналу управления могут быть получены из выражения частотной передаточной функции:

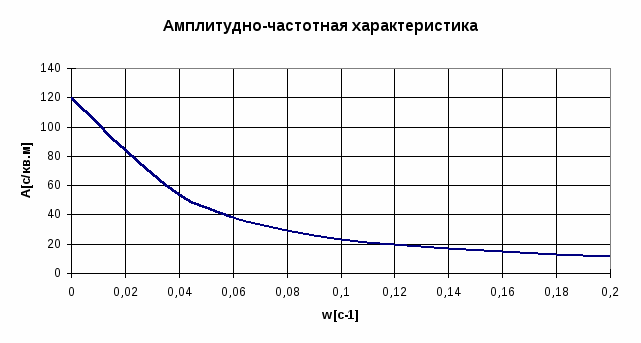
где А() - АЧХ объекта

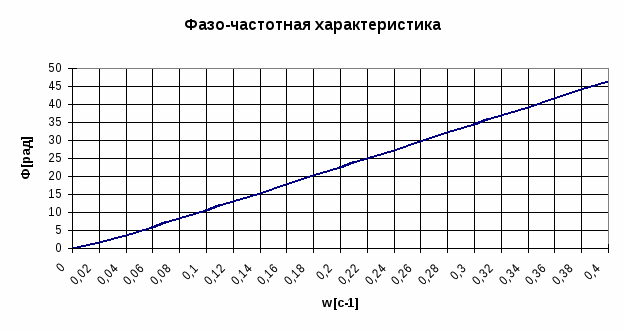
() - ФЧХ объекта

Зависимость отношения амплитуд выходных и входных колебаний от их частоты называется амплитудно-частотной характеристикой (АЧХ). Зависимость разности фазы выходных и входных колебаний от частоты называется фазо-частотной характеристикой (ФЧХ) системы.

Найдем модуль частотной передаточной функции (АЧХ):

(1^*)

Частота W_пр., определяющая полосу частот пропускания объекта, найдется из условия:

, подставляем в (1*)

, отсюда

Угол фазового сдвига находится как арктангенс отношения мнимой части комплексного числа к вещественной:

С учетом того, что К₀=112>0 выражение ФЧХ запишется в виде:

Частотные характеристики будем строить на диапазоне от 0 до 10 _пр.

Таблица 2

,

с^-1

0 0,02

0,04

0,06

0,08

0,1

0,12

0,14

0,16

0,18

0,2

АЧХ,

120,00

84,8528

53,6656

37,9473

29,1043

23,5339

19,7279

16,9706

14,8842

13,2518

11,9404

рад.

0,0000

1,6146

3,6929

5,9510

8,2742

10,6266

12,9944

15,3711

17,7536

20,1399

22,5289

Из графика АЧХ видно: чем меньше частота входного сигнала, тем больше этот сигнал усиливается. При  = 0 коэффициент усиления равен максимальному значению 112. При больших частотах выходная величина по модулю стремится к нулю. Такие сигналы объект не пропустит.

С ростом частоты увеличивается также фазовый сдвиг выходных колебаний по отношению к входным. Фазо-частотная характеристика положительна, следовательно, выходные колебания по фазе опережают входные. При  = ₀ () = .

Ре

y

y₀

y₁

ОШ

g

f1

[%конц]

[мА]

[%от.кл.]

[%конц]

[г/м²]

[%конц]

Ре

x_f

y₁

ОШ

g

f₁

y

[%от. кл]

[%конц]

Структурная схема системы регулирования

Структурная схема системы – графическое изображение АСР в виде совокупности динамических звеньев с указанием связей между ними.

Исходными данными для построения схемы служат передаточные функции звеньев.

По составленной схеме определяем передаточные функции системы:

1. Передаточная функция разомкнутой системы:

2.Передаточная функция замкнутой системы по каналу управления:

Передаточная функция замкнутой системы по возмущению в виде f₁

Построение области устойчивости системы.

1. Характеристический полином замкнутой системы получим из выражения:

Отсюда:

Д(р) =

2. Уравнение апериодической границы устойчивости соответствует при Р=0.

Получаем:

 К₂ = 0

Найдем колебательную границу устойчивости, для этого подставим:

Р=j

Тогда:

Решив уравнение относительно К₁ и К₂, найдем выражение для колебательной границы устойчивости в виде:

Рассчитываем три точки колебательной границы устойчивости при =0; ; 2.

 [c^-1]

0,005

0,01

К₁,

3,434

3,3191

2,8446

К₂,

0,0132

0,0382

СТУДЕНТ Ситников С.А. ГРУППА 2102

РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ (ЛИНИИ РАВНОГО ЗАПАСА УСТ.) НЕПРЕР.АСР

ПАРАМЕТРЫ МОДЕЛЕЙ ИЗВЕСТНОЙ ЧАСТИ СИСТЕМЫ

МОДЕЛЬ ОБЪЕКТА ПО КАНАЛУ УПРАВЛЕНИЯ :

коэффициент передачи объекта = 112.0000

постоянная времени объекта = 50.0000

запаздывание объекта = 120.0000

Коэф.передачи исполн.устройства = 1.0000

Коэф.передачи регулир.органа = 0.0104

Коэффициент передачи датчика = 0.2500

РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ

АПЕРИОДИЧЕСКАЯ ГРАНИЦА УСТОЙЧИВОСТИ K2 = 0

ТАБЛИЦА КОЛЕБАТЕЛЬНОЙ ГРАНИЦЫ УСТОЙЧИВОСТИ

W K1 K2

0.000000 -3.434066 0.000000

0.001538 -3.327219 0.001369

0.003077 -3.011959 0.005329

0.004615 -2.503887 0.011447

0.006154 -1.828233 0.019034

0.007692 -1.018726 0.027196

0.009231 -0.116080 0.034896

0.010769 0.833836 0.041032

0.012308 1.782074 0.044517

0.013846 2.678837 0.044370

0.015385 3.475768 0.039792

0.016923 4.128202 0.030245

0.018462 4.597282 0.015513

0.020000 4.851844 -0.004253

РАСЧЕТ ЛИНИИ РАВНОГО ЗАПАСА УСТОЙЧИВОСТИ

СТЕПЕНЬ КОЛЕБАТЕЛЬНОСТИ = 0.22

W K1 K2

0.000000 -3.434066 0.000000

0.001538 -2.954172 0.001362

0.003077 -2.334213 0.005027

0.004615 -1.620191 0.010232

0.006154 -0.858793 0.016105

0.007692 -0.095154 0.021747

0.009231 0.629134 0.026307

0.010769 1.277682 0.029049

0.012308 1.820598 0.029409

0.013846 2.235384 0.027029

0.015385 2.507436 0.021783

0.016923 2.630145 0.013783

0.018462 2.604631 0.003363

0.020000 2.439161 -0.008941

Область устойчивости системы в плоскости варьируемых параметров.

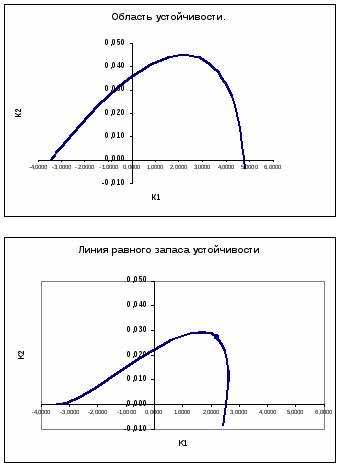
Определение направления штриховки колебательной границы устойчивости производится в соответствии со знаком определителя вида.

()= = =

При перемещении вдоль колебательной границы в направлении возрастании частоты от 0 до  кривая штрихуется слева, т. к.  > 0. Если частоту менять в пределах от -  до 0 ( < 0), то определитель меняет знак и, двигаясь вдоль увеличения частоты, нужно штриховать правую часть кривой. Таким образом, кривая колебательной границы проходится дважды, при этом штрихуется одна и та же часть кривой двойной штриховкой. Апериодическая граница устойчивости штрихуется в сторону колебательной границы устойчивости.

Параметры регулятора K₁ ; K₂, выбранные из области устойчивости системы, обеспечат затухание переходной составляющей её движения при любых начальных отклонениях и внешних воздействиях.

Расчет линии равного запаса устойчивости.

1.Выведем выражение расширенной АФЧХ регулирующего блока W_р.б.(m₁j)

Передаточная функция:

Заменим р на (j - m):

Запишем в виде

=, где

- расширенная АЧХ звена

-расширенная ФЧХ звена

Тогда:

2.Выведем выражение расширенной АФЧХ части системы, содержащей остальные элементы в контуре управления.

где

Заменим р на

, отсюда

Запишем в виде

Тогда:

Между заданной степенью колебательности m системы и характером расширенных и частотных характеристик с тем же m существует определенная связь. Для нахождения системы на границе заданной степени колебательности m, определяющей заданный запас устойчивости, необходимо выполнение следующего соотношения:

или в показательной форме

или

Получили два условия.

Первое условие приводит к уравнению:

Второе условие к уравнению вида:

Решив уравнение относительно К₁ и К₂ получим:

0,005

0,01

0,6

1,2

0,5646

0,932

0,8253

0,3642

1,1411

1,3021

-0,0089

-0,0059

-0,0032

0,0001

Все значения К₁ и К₂, лежащие на кривой обеспечат заданные запас устойчивости. Значения К₁ и К₂, лежащие внутри области, ограниченной данной кривой и осями координат, обеспечат запас больше заданного или степень затухания больше заданной, а лежащие вне этой области – степень затухания меньше заданной. Специальными исследованиями было установлено, что настройки, расположенные чуть правее экстремума линии равного запаса устойчивости, обеспечивают минимум квадратичного интегрального критерия качества, поэтому эти настройки можно назвать оптимальными.

Получение переходного процесса системы на заданный вид воздействия.

Рассмотрим операторный метод расчета непрерывных систем. Суть метода заключается в том, что каждый элемент непрерывной системы заменяется его дискретным аналогом, для этого вводим в модель непрерывного элемента импульсный элемент.

Дискретная модель системы.

f₁

g[n]

y₁[n]

x_f[n]

Ре[n]

y_c[n]

О б ъ е к т

Д а т ч и к

Р е г у л и р. б л о к

Импульсную модель элемента можно описать разностным уравнением, вид которого определяется формирующим элементом. Самым простым формирующим элементом является экстраполятор нулевого порядка с передаточной функцией вида:

, где Т₀ – период дискретности. Тогда дискретная передаточная функция непрерывного элемента найдётся как:

Выбор периода дискретности Т₀.

Допустимая погрешность моделирования определяется из условия выбора периода дискретности Т₀= Т/(10 15), где Т – постоянная времени системы, при этом должно выполнятся условие:  / Т₀ > 5  10, где  - запаздывание системы.

Дискретная модель объекта регулирования:

, где ; m = /T₀ (число тактов запаздывания – целое число).

Дискретная модель регулятора совместно с регулирующим блоком.

Дискретная модель датчика: W_дат (Z) = K_д = 0.25

Система разностных уравнений, описывающих работу данной АСР, при переходном процессе.

m = /T₀= 12 Тактов

Так как рассчитываем переходный процесс по задающему воздействию, то полагаем X_f = 0; Y_f = 0.

Уравнение регулируемого параметра:

y_c[n] = 0.8y_c[n - 1] + 22.4x[n - 13]

Уравнение датчика:

y₁[n] = К_дy_c[n] = 0.25y_c[n]

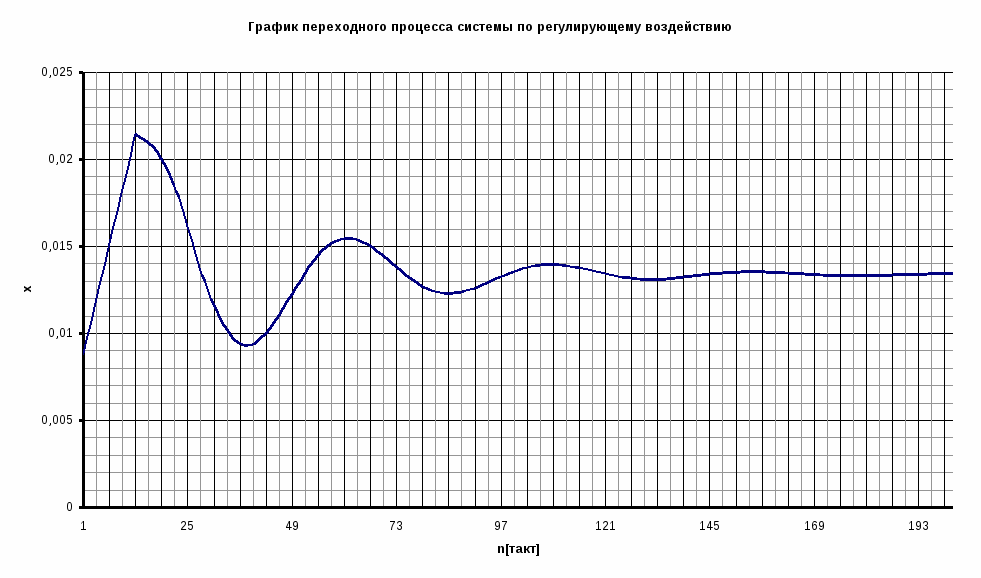
Уравнение элемента сравнения:

ОШ[n] = g К_д – y₁[n] = 0.375 - y₁[n]

Уравнение регулирующего воздействия:

X[n] = X[n - 1] + K_р_._о_. K₁ ОШ[n] + K_р_._о_.  (K₂ T₀ - K₁ ) ОШ[n - 1]

X[n] = X[n - 1] + 0.0232  ОШ[n] - 2.2316  ОШ[n - 1]

Выбираем параметры настройки ПИ регулятора:

K₁ = 2.234451

K₂ = 0.027039

Отклонение регулируемой величины от установившегося значения должно быть не более 5%.  = 0.05  | 1.5 | = 0.075

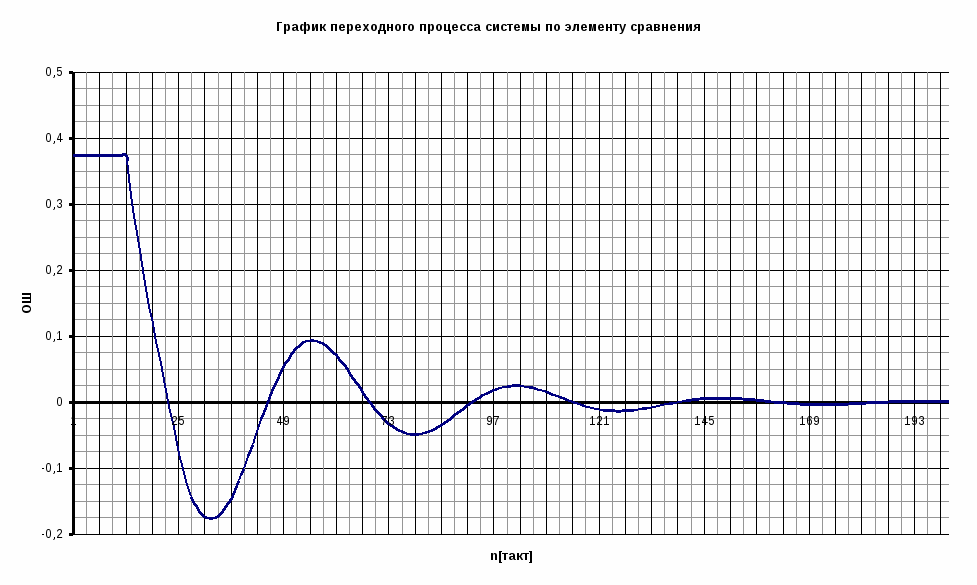
Расчёт переходного процесса системы по задающему воздействию

Yc[n]

Y1[n]

ОШ[n]

X[n]

-13

-130

-12

-120

-11

-110

-10

-100

-9

-90

-8

-80

-7

-70

-6

-60

-5

-50

-4

-40

-3

-30

-2

-20

-1

-10

0,375

0,008714

0,375

0,009769

0,375

0,010823

0,375

0,011878

0,375

0,012932

0,375

0,013987

0,375

0,015042

0,375

0,016096

0,375

0,017151

0,375

0,018205

100

0,375

0,01926

110

0,375

0,020314

120

0,375

0,021369

130

0,195197

0,048799

0,326201

0,021289

140

0,374977

0,093744

0,281256

0,021162

150

0,542423

0,135606

0,239394

0,020981

160

0,700002

0,175001

0,199999

0,020738

170

0,849687

0,212422

0,162578

0,020431

180

0,993058

0,248264

0,126736

0,020055

190

1,131376

0,282844

0,092156

0,019608

200

1,265653

0,316413

0,058587

0,019087

210

1,396697

0,349174

0,025826

0,018491

220

1,525154

0,381289

-0,00629

0,017817

230

1,651542

0,412885

-0,03789

0,017065

240

1,776274

0,444069

-0,06907

0,016234

250

1,899682

0,474921

-0,09992

0,015323

260

1,99663

0,499157

-0,12416

0,014479

270

2,071341

0,517835

-0,14284

0,013696

280

2,127036

0,531759

-0,15676

0,01297

290

2,166167

0,541542

-0,16654

0,012302

300

2,190591

0,547648

-0,17265

0,011692

310

2,201715

0,550429

-0,17543

0,011142

320

2,200597

0,550149

-0,17515

0,010655

330

2,188035

0,547009

-0,17201

0,010235

340

2,164623

0,541156

-0,16616

0,009888

350

2,130803

0,532701

-0,1577

0,009617

360

2,086905

0,521726

-0,14673

0,009428

370

2,033167

0,508292

-0,13329

0,009328

380

1,969768

0,492442

-0,11744

0,009321

390

1,900138

0,475034

-0,10003

0,009396

400

1,826891

0,456723

-0,08172

0,00954

410

1,752048

0,438012

-0,06301

0,009745

420

1,677207

0,419302

-0,0443

0,010003

430

1,603665

0,400916

-0,02592

0,010305

440

1,532508

0,383127

-0,00813

0,010646

450

1,464677

0,366169

0,008831

0,011017

460

1,401014

0,350254

0,024746

0,011412

470

1,342296

0,335574

0,039426

0,011822

480

1,289255

0,322314

0,052686

0,012241

490

1,242601

0,31065

0,06435

0,01266

500

1,203028

0,300757

0,074243

0,013071

510

1,171224

0,292806

0,082194

0,013465

520

1,147444

0,286861

0,088139

0,013834

530

1,13165

0,282912

0,092088

0,014174

540

1,123606

0,280901

0,094099

0,014479

550

1,122941

0,280735

0,094265

0,014748

560

1,129188

0,282297

0,092703

0,014977

570

1,141814

0,285453

0,089547

0,015164

580

1,160229

0,290057

0,084943

0,015309

590

1,183802

0,29595

0,07905

0,015411

600

1,21186

0,302965

0,072035

0,01547

610

1,243692

0,310923

0,064077

0,015488

620

1,278548

0,319637

0,055363

0,015466

630

1,315636

0,328909

0,046091

0,015406

640

1,354122

0,338531

0,036469

0,015312

650

1,393183

0,348296

0,026704

0,015187

660

1,432039

0,35801

0,01699

0,015037

670

1,469971

0,367493

0,007507

0,014864

680

1,506331

0,376583

-0,00158

0,014674

690

1,540544

0,385136

-0,01014

0,014471

700

1,572111

0,393028

-0,01803

0,014259

710

1,600609

0,400152

-0,02515

0,014043

720

1,625691

0,406423

-0,03142

0,013826

730

1,647084

0,411771

-0,03677

0,013614

740

1,664594

0,416149

-0,04115

0,013408

750

1,678103

0,419526

-0,04453

0,013214

760

1,687571

0,421893

-0,04689

0,013034

770

1,69304

0,42326

-0,04826

0,01287

780

1,69463

0,423658

-0,04866

0,012725

790

1,692528

0,423132

-0,04813

0,012601

800

1,68698

0,421745

-0,04675

0,012498

810

1,678283

0,419571

-0,04457

0,012417

820

1,666774

0,416693

-0,04169

0,012358

830

1,65282

0,413205

-0,0382

0,012322

840

1,636813

0,409203

-0,0342

0,012308

850

1,619159

0,40479

-0,02979

0,012314

860

1,600272

0,400068

-0,02507

0,01234

870

1,580568

0,395142

-0,02014

0,012384

880

1,560455

0,390114

-0,01511

0,012444

890

1,540327

0,385082

-0,01008

0,012519

900

1,520559

0,38014

-0,00514

0,012605

910

1,501498

0,375375

-0,00037

0,012701

920

1,483458

0,370865

0,004135

0,012805

930

1,466716

0,366679

0,008321

0,012914

940

1,451509

0,362877

0,012123

0,013026

950

1,438034

0,359509

0,015491

0,013138

960

1,426443

0,356611

0,018389

0,013249

970

1,416847

0,354212

0,020788

0,013357

980

1,409313

0,352328

0,022672

0,013459

990

1,403867

0,350967

0,024033

0,013554

100

1000

1,400495

0,350124

0,024876

0,013641

101

1010

1,399146

0,349787

0,025213

0,013719

102

1020

1,399735

0,349934

0,025066

0,013787

103

1030

1,402142

0,350536

0,024464

0,013843

104

1040

1,406225

0,351556

0,023444

0,013888

105

1050

1,411816

0,352954

0,022046

0,013922

106

1060

1,418727

0,354682

0,020318

0,013943

107

1070

1,426759

0,35669

0,01831

0,013954

108

1080

1,435702

0,358926

0,016074

0,013953

109

1090

1,445341

0,361335

0,013665

0,013943

110

1100

1,455459

0,363865

0,011135

0,013922

111

1110

1,465843

0,366461

0,008539

0,013893

112

1120

1,476287

0,369072

0,005928

0,013857

113

1130

1,486595

0,371649

0,003351

0,013813

114

1140

1,496584

0,374146

0,000854

0,013765

115

1150

1,506087

0,376522

-0,00152

0,013712

116

1160

1,514955

0,378739

-0,00374

0,013656

117

1170

1,523059

0,380765

-0,00576

0,013599

118

1180

1,530292

0,382573

-0,00757

0,01354

119

1190

1,536567

0,384142

-0,00914

0,013483

120

1200

1,541822

0,385456

-0,01046

0,013426

121

1210

1,546016

0,386504

-0,0115

0,013373

122

1220

1,549129

0,387282

-0,01228

0,013322

123

1230

1,551164

0,387791

-0,01279

0,013276

124

1240

1,552142

0,388035

-0,01304

0,013234

125

1250

1,552103

0,388026

-0,01303

0,013198

126

1260

1,551104

0,387776

-0,01278

0,013167

127

1270

1,549216

0,387304

-0,0123

0,013142

128

1280

1,546522

0,386631

-0,01163

0,013123

129

1290

1,543118

0,385779

-0,01078

0,01311

130

1300

1,539104

0,384776

-0,00978

0,013103

131

1310

1,534589

0,383647

-0,00865

0,013102

132

1320

1,529683

0,382421

-0,00742

0,013106

133

1330

1,524499

0,381125

-0,00612

0,013115

134

1340

1,519147

0,379787

-0,00479

0,013129

135

1350

1,513735

0,378434

-0,00343

0,013147

136

1360

1,508368

0,377092

-0,00209

0,013169

137

1370

1,503141

0,375785

-0,00079

0,013193

138

1380

1,498143

0,374536

0,000464

0,01322

139

1390

1,493454

0,373364

0,001636

0,013249

140

1400

1,489144

0,372286

0,002714

0,013278

141

1410

1,485272

0,371318

0,003682

0,013308

142

1420

1,481884

0,370471

0,004529

0,013338

143

1430

1,479017

0,369754

0,005246

0,013368

144

1440

1,476696

0,369174

0,005826

0,013396

145

1450

1,474932

0,368733

0,006267

0,013423

146

1460

1,473728

0,368432

0,006568

0,013447

147

1470

1,473076

0,368269

0,006731

0,013469

148

1480

1,472957

0,368239

0,006761

0,013489

149

1490

1,473344

0,368336

0,006664

0,013506

150

1500

1,474201

0,36855

0,00645

0,01352

151

1510

1,475489

0,368872

0,006128

0,01353

152

1520

1,477158

0,369289

0,005711

0,013538

153

1530

1,479157

0,369789

0,005211

0,013542

154

1540

1,481431

0,370358

0,004642

0,013544

155

1550

1,483924

0,370981

0,004019

0,013542

156

1560

1,486576

0,371644

0,003356

0,013538

157

1570

1,48933

0,372332

0,002668

0,013532

158

1580

1,49213

0,373032

0,001968

0,013523

159

1590

1,494921

0,37373

0,00127

0,013512

160

1600

1,497653

0,374413

0,000587

0,0135

161

1610

1,500278

0,375069

-6,9E-05

0,013486

162

1620

1,502753

0,375688

-0,00069

0,013472

163

1630

1,505042

0,37626

-0,00126

0,013456

164

1640

1,507111

0,376778

-0,00178

0,013441

165

1650

1,508936

0,377234

-0,00223

0,013425

166

1660

1,510495

0,377624

-0,00262

0,01341

167

1670

1,511775

0,377944

-0,00294

0,013395

168

1680

1,512766

0,378192

-0,00319

0,013381

169

1690

1,513468

0,378367

-0,00337

0,013368

170

1700

1,513882

0,37847

-0,00347

0,013356

171

1710

1,514017

0,378504

-0,0035

0,013346

СТУДЕНТ Ситников С.А. ГРУППА 2102

ИССЛЕДОВАНИЕ ЛИНЕЙНОЙ АСР ПРИ РАЗЛИЧНЫХ ВОЗДЕЙСТВИЯХ

МОДЕЛЬ ОБЪЕКТА ПО КАНАЛУ УПРАВЛЕНИЯ :

коэффициент передачи объекта = 112.0000

постоянная времени объекта = 50.0000

запаздывание объекта = 120.0000

Коэф.передачи исполн.устройства = 1.0000

Коэф.передачи регулир.органа = 0.0104

Коэффициент передачи датчика = 0.2500

ПЕРЕХОДНЫЙ ПРОЦЕСС ПО ЗАДАЮЩЕМУ ВОЗДЕЙСТВИЮ

Изменение задающего воздействия = 1.5000

ПИ - закон регулирования

Параметры закона регулирования :

Пропорциональная составляющая K1 = 2.2345

Интегральная составляющая K2 = 0.0270

Дискретность счета переходного процесса = 10.0000

ВРЕМЯ ЗАДАНИЕ РЕГ ОРГАН СИСТЕМА Ср.Квад.Ош.

160.0000000 1.5000000 0.0210865 0.6510940 0.1252132

170.0000000 1.5000000 0.0208436 0.7956272 0.1199796

180.0000000 1.5000000 0.0205269 0.9353699 0.1147136

190.0000000 1.5000000 0.0201348 1.0711906 0.1095526

200.0000000 1.5000000 0.0196659 1.2038003 0.1045969

210.0000000 1.5000000 0.0191190 1.3337810 0.0999210

220.0000000 1.5000000 0.0184932 1.4616092 0.0955806

230.0000000 1.5000000 0.0177878 1.5876752 0.0916181

240.0000000 1.5000000 0.0170022 1.7122984 0.0880660

250.0000000 1.5000000 0.0161358 1.8357403 0.0849498

260.0000000 1.5000000 0.0153094 1.9373479 0.0822463

270.0000000 1.5000000 0.0145229 2.0198114 0.0799121

280.0000000 1.5000000 0.0137772 2.0852575 0.0778947

290.0000000 1.5000000 0.0130747 2.1353655 0.0761392

300.0000000 1.5000000 0.0124183 2.1714592 0.0745921

310.0000000 1.5000000 0.0118120 2.1945815 0.0732034

320.0000000 1.5000000 0.0112599 2.2055516 0.0719279

330.0000000 1.5000000 0.0107670 2.2050126 0.0707261

340.0000000 1.5000000 0.0103385 2.1934679 0.0695641

350.0000000 1.5000000 0.0099797 2.1713114 0.0684141

360.0000000 1.5000000 0.0096963 2.1388500 0.0672545

370.0000000 1.5000000 0.0094943 2.0963225 0.0660695

380.0000000 1.5000000 0.0093795 2.0439143 0.0648495

390.0000000 1.5000000 0.0093439 1.9842299 0.0635947

400.0000000 1.5000000 0.0093801 1.9193960 0.0623117

410.0000000 1.5000000 0.0094816 1.8511763 0.0610116

420.0000000 1.5000000 0.0096421 1.7810594 0.0597076

430.0000000 1.5000000 0.0098554 1.7103270 0.0584134

440.0000000 1.5000000 0.0101155 1.6401055 0.0571426

450.0000000 1.5000000 0.0104161 1.5714055 0.0559073

460.0000000 1.5000000 0.0107508 1.5051522 0.0547178

470.0000000 1.5000000 0.0111129 1.4422078 0.0535822

480.0000000 1.5000000 0.0114952 1.3833890 0.0525060

490.0000000 1.5000000 0.0118904 1.3294795 0.0514923

500.0000000 1.5000000 0.0122905 1.2812400 0.0505413

510.0000000 1.5000000 0.0126873 1.2394150 0.0496509

520.0000000 1.5000000 0.0130736 1.2044481 0.0488171

530.0000000 1.5000000 0.0134435 1.1765553 0.0480342

540.0000000 1.5000000 0.0137915 1.1557790 0.0472955

550.0000000 1.5000000 0.0141134 1.1420267 0.0465939

560.0000000 1.5000000 0.0144053 1.1350983 0.0459225

570.0000000 1.5000000 0.0146642 1.1347064 0.0452745

580.0000000 1.5000000 0.0148874 1.1404887 0.0446441

590.0000000 1.5000000 0.0150731 1.1520182 0.0440261

600.0000000 1.5000000 0.0152202 1.1688082 0.0434168

610.0000000 1.5000000 0.0153281 1.1903172 0.0428132

620.0000000 1.5000000 0.0153969 1.2159499 0.0422137

630.0000000 1.5000000 0.0154275 1.2450597 0.0416176

640.0000000 1.5000000 0.0154214 1.2769482 0.0410251

650.0000000 1.5000000 0.0153810 1.3108999 0.0404374

660.0000000 1.5000000 0.0153088 1.3462052 0.0398559

670.0000000 1.5000000 0.0152080 1.3821778 0.0392826

680.0000000 1.5000000 0.0150817 1.4181646 0.0387193

690.0000000 1.5000000 0.0149337 1.4535546 0.0381681

700.0000000 1.5000000 0.0147675 1.4877838 0.0376307

710.0000000 1.5000000 0.0145869 1.5203400 0.0371084

720.0000000 1.5000000 0.0143958 1.5507661 0.0366022

730.0000000 1.5000000 0.0141981 1.5786632 0.0361128

740.0000000 1.5000000 0.0139974 1.6036936 0.0356403

750.0000000 1.5000000 0.0137973 1.6255834 0.0351843

760.0000000 1.5000000 0.0136013 1.6441261 0.0347442

770.0000000 1.5000000 0.0134125 1.6591849 0.0343191

780.0000000 1.5000000 0.0132337 1.6706932 0.0339077

790.0000000 1.5000000 0.0130675 1.6786501 0.0335088

800.0000000 1.5000000 0.0129159 1.6831170 0.0331210

810.0000000 1.5000000 0.0127808 1.6842113 0.0327430

820.0000000 1.5000000 0.0126636 1.6821010 0.0323734

830.0000000 1.5000000 0.0125652 1.6769990 0.0320113

840.0000000 1.5000000 0.0124864 1.6691563 0.0316558

850.0000000 1.5000000 0.0124273 1.6588563 0.0313060

860.0000000 1.5000000 0.0123879 1.6464083 0.0309616

870.0000000 1.5000000 0.0123679 1.6321418 0.0306222

880.0000000 1.5000000 0.0123664 1.6163996 0.0302876

890.0000000 1.5000000 0.0123826 1.5995315 0.0299579

900.0000000 1.5000000 0.0124151 1.5818878 0.0296333

910.0000000 1.5000000 0.0124626 1.5638131 0.0293140

920.0000000 1.5000000 0.0125233 1.5456400 0.0290002

930.0000000 1.5000000 0.0125955 1.5276845 0.0286922

940.0000000 1.5000000 0.0126774 1.5102410 0.0283902

950.0000000 1.5000000 0.0127670 1.4935793 0.0280945

960.0000000 1.5000000 0.0128624 1.4779404 0.0278052

970.0000000 1.5000000 0.0129615 1.4635353 0.0275223

980.0000000 1.5000000 0.0130627 1.4505419 0.0272459

990.0000000 1.5000000 0.0131639 1.4391047 0.0269757

1000.0000000 1.5000000 0.0132635 1.4293337 0.0267117

1010.0000000 1.5000000 0.0133598 1.4213046 0.0264537

1020.0000000 1.5000000 0.0134514 1.4150592 0.0262012

1030.0000000 1.5000000 0.0135370 1.4106063 0.0259541

1040.0000000 1.5000000 0.0136154 1.4079236 0.0257119

1050.0000000 1.5000000 0.0136857 1.4069599 0.0254745

ПЕРЕХОДНЫЙ ПРОЦЕСС ПО ВОЗМУЩЕНИЮ НА ВЫХОДЕ ОБЪЕКТА

Канал передачи возмущения - апериодическое звено 1 порядка

ПАРАМЕТРЫ КАНАЛА ПЕРЕДАЧИ ВОЗМУЩЕНИЯ

Коэффициент передачи канала возмущения = 1.1000

Постоянная времени канала возмущения = 60.0000

Возмущение ступенчатое

Значение возмущения = -3.0000

Дискретность счета переходного процесса = 10.0000

ВРЕМЯ ВОЗМ YF ОБЪЕКТ СИСТЕМА Ср.Квад.Ош.

0.000000 0.000000 0.000000 0.000000 0.000000

30.000000 -1.298449 0.000000 -1.298449 0.044026

60.000000 -2.085998 0.000000 -2.085998 0.118114

90.000000 -2.563671 0.000000 -2.563671 0.192940

120.000000 -2.853394 0.000000 -2.853394 0.258957

150.000000 -3.029119 0.166485 -2.862634 0.309076

180.000000 -3.135703 0.677008 -2.458695 0.327872

210.000000 -3.200349 1.349803 -1.850546 0.319704

240.000000 -3.239558 2.095556 -1.144002 0.295999

270.000000 -3.263340 2.864540 -0.398801 0.267365

300.000000 -3.277765 3.543583 0.265818 0.241694

330.000000 -3.286514 4.047102 0.760588 0.222506

360.000000 -3.291820 4.348739 1.056918 0.209291

390.000000 -3.295039 4.444880 1.149841 0.199622

420.000000 -3.296991 4.350097 1.053106 0.190957

450.000000 -3.298175 4.112383 0.814208 0.181841

480.000000 -3.298893 3.791970 0.493077 0.172135

510.000000 -3.299329 3.447541 0.148213 0.162485

540.000000 -3.299593 3.132691 -0.166902 0.153660

570.000000 -3.299753 2.889637 -0.410116 0.146089

600.000000 -3.299850 2.742393 -0.557457 0.139726

630.000000 -3.299909 2.697175 -0.602735 0.134214

660.000000 -3.299945 2.745037 -0.554908 0.129137

690.000000 -3.299967 2.864856 -0.435111 0.124222

720.000000 -3.299980 3.028208 -0.271771 0.119399

750.000000 -3.299988 3.204946 -0.095042 0.114750

780.000000 -3.299993 3.367705 0.067713 0.110398

810.000000 -3.299996 3.495293 0.195298 0.106417

840.000000 -3.299997 3.574872 0.274874 0.102802

870.000000 -3.299999 3.602518 0.302519 0.099485

900.000000 -3.299999 3.582358 0.282359 0.096382

930.000000 -3.299999 3.524734 0.224735 0.093427

960.000000 -3.300000 3.443767 0.143768 0.090596

990.000000 -3.300000 3.354732 0.054732 0.087893

1020.000000 -3.300000 3.271678 -0.028322 0.085333

1050.000000 -3.300000 3.205611 -0.094388 0.082929

1080.000000 -3.300000 3.163383 -0.136617 0.080673

1110.000000 -3.300000 3.147352 -0.152648 0.078549

1140.000000 -3.300000 3.155744 -0.144256 0.076536

1170.000000 -3.300000 3.183554 -0.116446 0.074616

Определение показателей качества системы регулирования.

Оценку качества работы системы можно получить, анализируя кривую переходного процесса системы на заданный вид воздействия.

По задающему воздействию:

Точность системы управления в установившемся режиме работы.

Этот показатель оценивается величиной установившейся ошибки: ОШ_ - точность, с которой поддерживается постоянство регулируемого параметра, определятся как разность между установившимся значением регулируемой величины после окончания переходного процесса y_ и её заданным значением g_зад, т.е. ОШ_ = y_ - g_зад Из графика видно, что

y_ = g_зад = 1.5. это значит, что величина установившейся ошибки ОШ_ = 0, т.е. полученная система не имеет систематической ошибки, сигнал на выходе системы, в установившемся режиме, равен сигналу задания.

Оценка быстродействия системы.

Быстродействие системы оценивается по времени переходного процесса, от момента начала воздействия до момента времени, после которого верно неравенство: | y(t) - y_ |  , где  = (0.05  y_ ).

По графику переходного процесса найдём t_п.пр. = 1070с  18 мин.

Длительность переходного процесса велика.

Запас устойчивости (склонность системы к колебательности).

а). перерегулирование – максимальное отклонение регулируемой переменной от установившегося значения.

Величина  - велика, (допускается 10  30 %).

б). затухание за период.

Затухание в допустимых пределах.

в). число колебаний за время переходного процесса – 2.

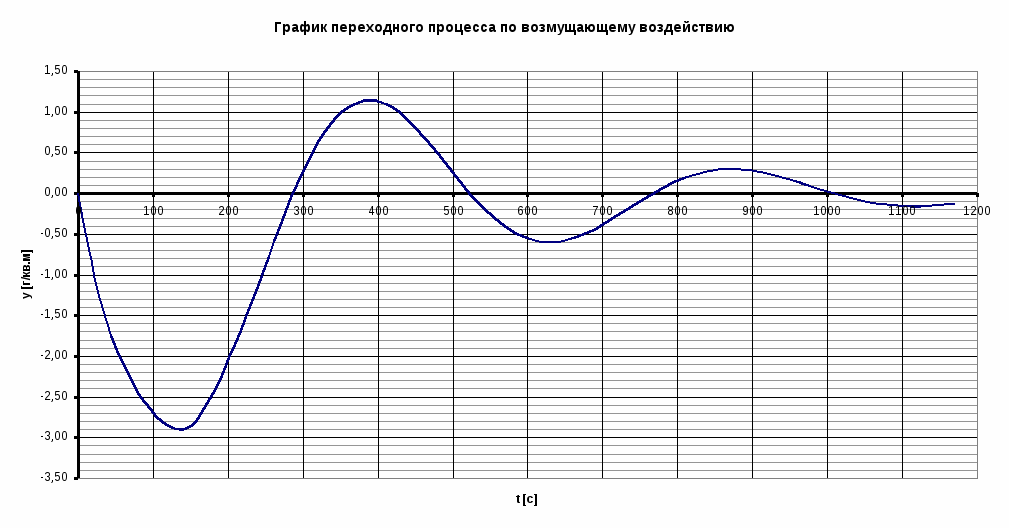
По возмущающему воздействию:

1. Оценка быстродействия системы.

По графику переходного процесса найдём t_п.пр. = 700с  11 мин.

2. Запас устойчивости (склонность системы к колебательности).

а). перерегулирование – максимальное отклонение регулируемой переменной от установившегося значения.

Величина  - хороший показатель, (допускается 10  30 %).

б). затухание за период.

Затухание в допустимых пределах.

в). число колебаний за время переходного процесса – 1.

Анализ полученных результатов

Получили систему управления не обладающую статической ошибкой, имеющую хороший запас устойчивости, лежащий в пределах общетехнических нормативов.

За счёт снижения точности работы системы в установившемся режиме до допустимого значения можно несколько повысить запас устойчивости, выбрав другие настройки ПИ-регулятора.

Для выполнения более высоких требований к качеству переходного процесса можно ввести в систему дополнительно специальные корректирующие звенья с особо подобранной передаточной функцией, заменить регулятор с ПИ-законом регулирования на более сложный регулятор с ПИД-законом регулирования