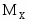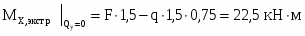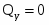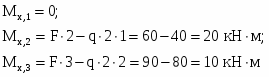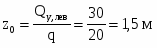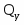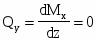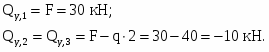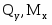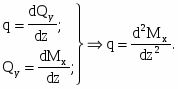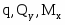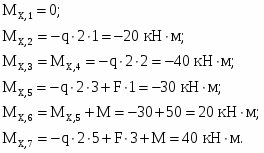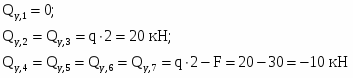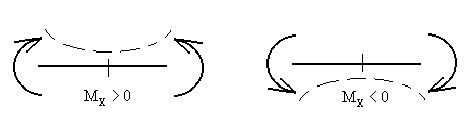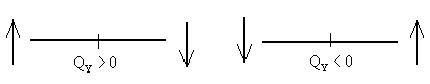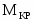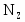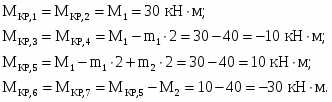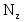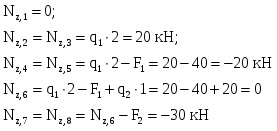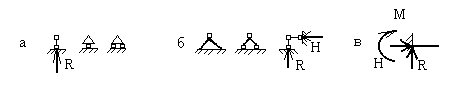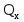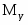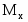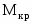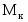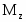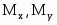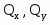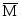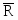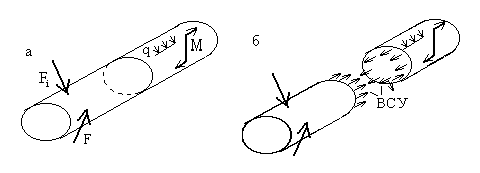Построение эпюр внутренних силовых факторов

Внутренние силы упругости. Метод сечений

Рассмотрим тело произвольной формы в “спокойном”, ненагруженном состоянии. Между его частицами всегда существуют силы взаимодействия, которые стремятся сохранить его как единое целое, то есть препятствуют изменению взаимного расположения частиц. При нагружении тела произвольной внешней нагрузкой силы взаимодействия между частицами изменяются, появляются дополнительные силы взаимодействия, которые приводят к изменению взаимного расположения частиц тела, то есть к его деформации.

Эти дополнительные силы взаимодействия называются внутренними силами упругости (ВСУ) и являются предметом изучения сопротивления материалов.

Анализ характера распределения внутренних сил упругости осуществляется при помощи метода сечений. Рассмотрим тело произвольной формы, нагруженное самоуравновешенной системой сил (рис.1,а). В интересующем нас сечении мысленно рассечем его плоскостью на две части (рис.1,б)

Рис. 1

Внутренние силы упругости определяют взаимодействие между частицами тела, расположенными по разные стороны от мысленно проведенного сечения. В разных сечениях тела возникают разные внутренние силы упругости, но по принципу действия и противодействия они всегда взаимны. Правая отсеченная часть тела действует на левую точно так же, как и левая на правую, а это означает, что равнодействующая внутренних сил может определяться из условий равновесия как левой отсеченной части тела, так и правой.

Из курса теоретической механики известно, что любую произвольную систему сил можно привести к центру тяжести сечения. В результате внутренние силы упругости, действующие в рассматриваемом сечении, приводятся к главному вектору и главному моменту . Выберем прямоугольную систему координат OXYZ так, что ось Z будет направлена по нормали к поперечному сечению, а оси X и Y лежат в плоскости сечения. Проектируя главный вектор на каждую из осей, а главный момент на каждую из координатных плоскостей, получим шесть величин - 3 силы и 3 момента, - которые называются внутренними силовыми факторами (рис.2).

Рис. 2

Полученные таким образом 6 внутренних силовых факторов (ВСФ) имеют строго определенные названия:

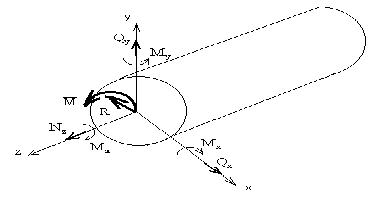
- продольная (нормальная) сила;

-поперечная (перерезывающая) сила;

- изгибающий момент;

- крутящий момент.

Иногда обозначение заменяют на или , более точно отвечающие физическому смыслу этой величины.

График, показывающий как меняется внутренний силовой фактор по длине рассматриваемого тела, называется эпюрой.

Правильность построения эпюры обеспечивается, в первую очередь, надлежащим выбором характерных сечений, то есть тех сечений, в которых величина внутреннего силового фактора обязательно должна быть определена.

К характерным сечениям относятся:

1. сечения, расположенные бесконечно близко по обе стороны от точек приложения сосредоточенных сил и моментов;

2. сечения, расположенные в начале и в конце каждого участка с распределенной нагрузкой;

3. сечения, расположенные бесконечно близко к опорам, а также на свободных концах.

Виды сопротивлений

В зависимости от характера внешней нагрузки и от особенностей нагружаемого тела, в поперечных сечениях могут возникать не все шесть внутренних силовых факторов, а какой-либо один или некоторая их комбинация. В соответствии с этим различают следующие виды сопротивлений.

Растяжение (или сжатие) - это вид сопротивления, при котором во всех поперечных сечениях возникает только продольная сила .

Кручение - это вид сопротивления, при котором во всех поперечных сечениях возникает только крутящий момент .

Чистый изгиб - это вид сопротивления, при котором во всех поперечных сечениях возникает только изгибающий момент (или). Чаще всего изгибающий момент сопровождается наличием поперечной силы (или момент сопровождается наличием поперечной силы ). В этом случае имеет место поперечный изгиб.

Возможны случаи, когда в поперечных сечениях возникают два и более внутренних силовых фактора одновременно (исключая их комбинации, рассмотренные выше), тогда говорят о сложном сопротивлении..

Виды опорных закреплений

С технической точки зрения опорные закрепления конструкций весьма разнообразны. При формировании расчетной схемы все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых наиболее часто встречаются: шарнирно-подвижная опора (возможные обозначения для нее представлены на рис.3,а), шарнирно-неподвижная опора (рис.3,б) и жесткое защемление, или заделка (рис.3,в).

Рис. 3

В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.

В шарнирно-неподвижной опоре возникают вертикальная и горизонтальная реакции. Здесь невозможны перемещения по направлениям опорных стержней, но допускается поворот опорного сечения.

В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный (реактивный) момент. При этом опорное сечение не может смещаться и поворачиваться.

При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять, выбирая при этом отсеченную часть так, чтобы заделка с неизвестными реакциями в нее не попадала. При расчете систем на шарнирных опорах реакции опор должны быть определены обязательно. Уравнения статики, используемые для этого, зависят от вида системы (балка, рама и др.) и будут приведены в соответствующих разделах настоящего пособия.

Построение эпюр продольных сил

Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.

Правило знаков для : условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной - в противном случае.

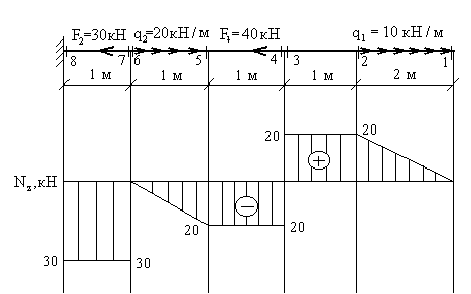
Пример 1. Построить эпюру продольных сил для жестко защемленной балки (рис.4).

Порядок расчета:

1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.

2. Определяем продольную силу в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

3. По найденным значениям строим эпюру .

Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные - под осью.

Рис. 4

Построение эпюр крутящих моментов

Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.

Правило знаков для : условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным - в противном случае.

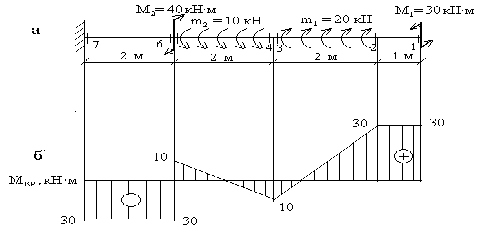
Пример 2. Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5,а).

Порядок расчета.

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1.Намечаем характерные сечения.

2.Определяем крутящий момент в каждом характерном сечении.

3.По найденным значениям строим эпюру (рис.5,б).

Рис. 5

Правила контроля эпюр и

Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.

1. Эпюры и всегда прямолинейные.

2. На участке, где нет распределенной нагрузки, эпюра () - прямая, параллельная оси; а на участке под распределенной нагрузкой - наклонная прямая.

3. Под точкой приложения сосредоточенной силы на эпюре обязательно должен быть скачок на величину этой силы, аналогично под точкой приложения сосредоточенного момента на эпюре будет скачок на величину этого момента.

Построение эпюр поперечных сил и изгибающих моментов в балках

Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора - поперечная сила и изгибающий момент .

Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.

Правило знаков для : условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной - в противном случае.

Схематически это правило знаков можно представить в виде

Изгибающий момент в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.

Правило знаков для : условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной - в противном случае.

Схематически это правило знаков можно представить в виде:

Следует отметить, что при использовании правила знаков для в указанном виде, эпюра всегда оказывается построенной со стороны сжатых волокон балки.

Консольные балки

При построении эпюр и в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

Пример 3. Построить эпюры и (рис.6).

Рис. 6

Порядок расчета.

1. Намечаем характерные сечения.

2. Определяем поперечную силу в каждом характерном сечении.

По вычисленным значениям строим эпюру .

3. Определяем изгибающий момент в каждом характерном сечении.

По вычисленным значениям строим эпюру , причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.

Дифференциальные зависимости между

Указанные зависимости используются при построении эпюр , поэтому приведем их здесь без соответствующего вывода, который дается в лекционном курсе.

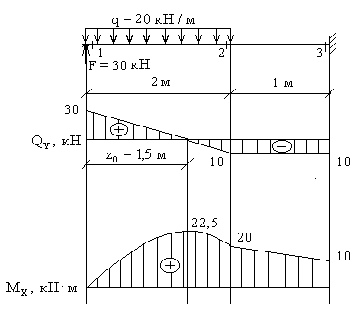
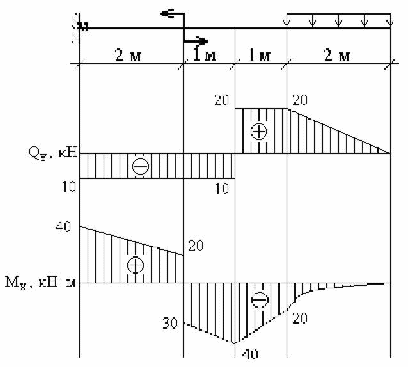
Пример 4. Построить эпюры (рис.7).

В данном случае для правильного построения эпюры необходимо использовать приведенные выше дифференциальные зависимости.

Порядок расчета.

1. Намечаем характерные сечения.

2. Определяем поперечные силы в характерных сечениях.

Строим эпюру .

Характер эпюры, то есть тот факт, что эпюра пересекает ось, говорит о том, что в этом сечении момент будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении , а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.

Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры разделить на интенсивность распределенной нагрузки q:

Рис. 7

Определяем изгибающие моменты в характерных сечениях.

4. Вычисляем экстремальное значение изгибающего момента в сечении, где :

Строим эпюру .

Литература:

1. Авдотьин Л.H., Лежава И.Г., Смоляр И.М. Градостроительное проектирование. Учебник для вузов. - М.: Стройиздат, 1989.

2. Архитектура гражданских и промышленны зданий. Т.2 «Основы проектирования» под ред. Предтеченского В.М. –М.: Стройиздат, 1976. 214 с.

3. Архитектура гражданских и промышленных зданий т.3 «Жилые здания» под ред. Шевцова К.К. –М.: Стройиздат, 1982. 239 с.

4. Архитектура гражданских и промышленных зданий т.5 «Промышленные здания» под ред. Шубина Л.Ф. –М.: Стройиздат, 1986. 239 с.

5. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции: Общий курс. – М.: Стройиздат, 1991. - 768 с.

6. БНІП 2.02.01-83 Будівельні норми і правила. Норми проектування основ будівельників та споруд. М: Будвидав. 1985

7. Горохов В.А. и др. Инженерное благоустройство городских территорий, М.: Стройиздат, 1986.

8. Губень П.І. Проблеми ціноутворення в умовах ринкових відносин та шляхи їх подолання. – „Вісник Академії будівництва України”. 2000, № 8. с.19-22.

9. Долматов Б.І. Механіка грунтів, основи та фундаменти. – М. Будвидав, 1990

10. Дикман Л.Г. Организация и планирование строительного производства. – М.: Высшая школа, 1988. – 559 с.