Конспект урока на тему «Тригонометрические выражения и их преобразования»
Воронкова Ольга Ивановна
МБОУ «Средняя общеобразовательная школа
№ 18»
г. Энгельса Саратовской области.
Учитель математики.
«Тригонометрические выражения и их преобразования»
Содержание
Введение …………………………………………………………………………....3
Глава 1 Классификация заданий на использование преобразований тригонометрических выражений ………………………….……………………...5
1.1. Задания на вычисление значений тригонометрических выражений……….5
1.2. Задания на упрощение тригонометрических выражений.... 7
1.3. Задания на преобразование числовых тригонометрических выражений…..7
1.4 Задания смешанного типа…………………………………………………….....9
Глава 2. Методические аспекты организация итогового повторения темы «Преобразование тригонометрических выражений»……………………………11
2.1 Тематическое повторение в 10 классе………………………………………...11
Тест 1………………………………………………………………………………..12
Тест 2………………………………………………………………………………..13
Тест 3………………………………………………………………………………..14
2.2 Итоговое повторение в 11 классе……………………………………………...15
Тест 1………………………………………………………………………………..17
Тест 2………………………………………………………………………………..17
Тест 3………………………………………………………………………………..18
Заключение .…………………………………………………………………….......19
Список использованной литературы………………………………………..…….20
Введение.
В сегодняшних условиях наиболее главным является вопрос: «Как мы можем помочь устранить некоторые пробелы в знаниях обучающихся и предостеречь их от возможных ошибок на ЕГЭ?» Для решения этого вопроса надо добиваться от учащихся не формального усвоения программного материала, а его глубокого и осознанного понимания, развития скорости устных вычислений и преобразований, а также развития навыков решения простейших задач «в уме». Необходимо убеждать учеников в том, что лишь при наличии активной позиции, при изучении математики, при условии обретения практических умений, навыков и их использования, можно рассчитывать на реальный успех. Нужно использовать любую возможность для подготовки к ЕГЭ, в том числе и элективные предметы в 10-11-х классах, регулярно проводить разбор сложных заданий с обучающимися, выбирая самый рациональный способ решения на уроках и дополнительных занятиях. Положительный результат в области решения типовых задач может быть достигнут, если учителя математики, будут, создавая хорошую базовую подготовку обучающихся, искать новые пути в решении открывшихся перед нами проблем, активно экспериментировать, применять современные педагогические технологии, методы, приёмы, создающие благоприятные условия для эффективной самореализации и самоопределения обучающихся в новых социальных условиях.
Тригонометрия – составная часть школьного курса математики. Хорошие знания и прочные навыки по тригонометрии являются свидетельством достаточного уровня математической культуры, непременным условием успешного изучения в вузе математики, физики, ряда технических дисциплин.
Актуальность работы. Значительная часть выпускников школ показывает из года в год весьма слабую подготовку по этому важному разделу математики, о чём свидетельствуют результаты прошлых лет ( процент выполнения 2011- 48,41%, 2012-51,05%), так как анализ сдачи единого государственного экзамена показал, что ученики допускают много ошибок при выполнении заданий именно этого раздела или вообще не берутся за такие задания. В Едином государственном экзамене вопросы по тригонометрии встречаются почти в трех видах заданий. Это и решение простейших тригонометрических уравнений в задании В5, и работа с тригонометрическими выражениями в задании В7, и исследование тригонометрических функций в задании В14, а так же задания В12, в которых имеются формулы, описывающие физические явления и содержащие тригонометрические функции. И это – только часть заданий В! А ведь ещё есть и любимые тригонометрические уравнения с отбором корней С1, и «не очень любимые» геометрические задания С2 и С4.
Цель работы. Проанализировать материал ЕГЭ заданий В7, посвященных преобразованиям тригонометрических выражений и проклассифицировать задания по форме подачи их в тестах.
Работа состоит из двух глав, введения и заключения. Во введении подчеркнута актуальность работы. В первой главе приведена классификация заданий на использование преобразований тригонометрических выражений в тестовых заданиях ЕГЭ (2012 г).
Во второй главе рассмотрена организация повторения темы «Преобразование тригонометрических выражений» в 10, 11 классах и разработаны тесты по данной теме.
Список литературы включает 17 источников.
Глава 1. Классификация заданий на использование преобразований тригонометрических выражений.
В соответствии со стандартом среднего (полного) образования и требованиями к уровню подготовки учащихся в кодификатор требований включаются задания на знания основ тригонометрии.
Изучение основ тригонометрии будет наиболее эффективным, когда:
будет обеспечена положительная мотивация учащихся на повторение ранее изученного материала;
в учебном процессе будет реализован личностно-ориентированный подход;
будет применяться система задач, которая способствует расширению, углублению, систематизации знаний учащихся;
содержание повторяемого материала и способы его подачи будут способствовать активизации мыслительной деятельности учащихся на уроках и в процессе самостоятельного приобретения знаний;
будут использоваться передовые педагогические технологии.
Проанализировав литературу и интернет-ресурсы по подготовке к ЕГЭ, нами предложена одна из возможных классификаций заданий В7 (КИМ ЕГЭ 2012-тригонометрия): задания на вычисление значений тригонометрических выражений; задания на преобразование числовых тригонометрических выражений; задания на преобразование буквенных тригонометрических выражений; задания смешанного типа.
1.1. Задания на вычисление значений тригонометрических выражений.
Одним из наиболее распространенных типов несложных задач по тригонометрии является вычисление значений тригонометрических функций по значению одной из них:
а) Использование основного тригонометрического тождества и его следствия.
Пример 1. Найдите ![]() , если
, если ![]() и
и ![]() .
.
Решение. ![]() ,
, ![]() ,
,
![]() .
.
Т.к. ![]() , то
, то ![]() .
.
Ответ. ![]()
Пример 2. Найдите ![]() , если
, если ![]() и
и ![]() .
.
Решение. ![]() ,
, ![]() ,
, 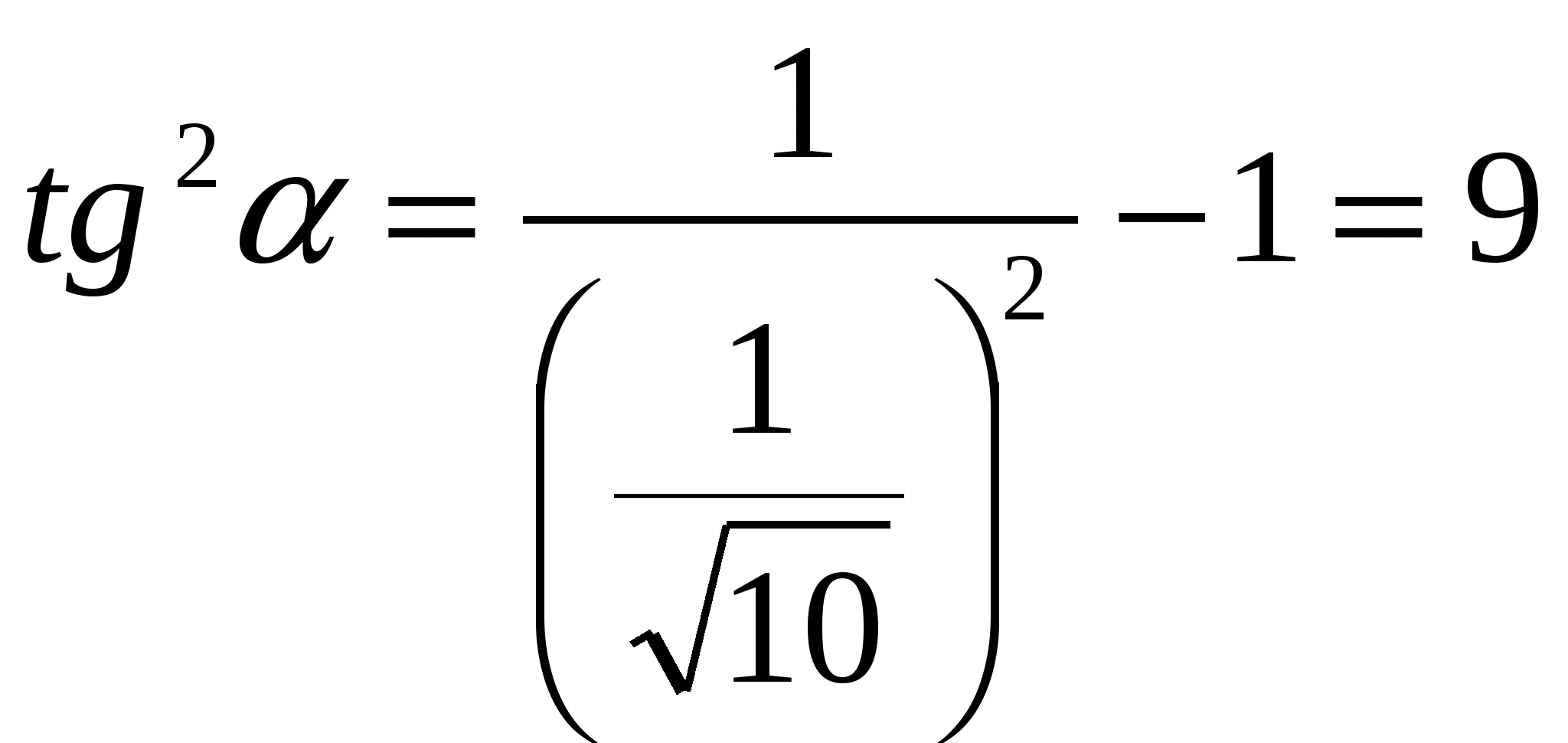 .
.
Т.к. ![]() , то
, то ![]() .
.
Ответ. ![]() .
.
б) Использование формул двойного угла.
Пример 3. Найдите ![]() , если
, если ![]() .
.
Решение. ![]() ,
, ![]()
![]() .
.
Ответ. ![]() .
.
Пример 4. Найдите значение выражения ![]() .
.
Решение. ![]() .
.
Ответ. ![]() .
.
Задания для самостоятельного решения:
1. Найдите ![]() , если
, если ![]() и
и ![]() . Ответ. -0,2
. Ответ. -0,2
2. Найдите ![]() , если
, если ![]() и
и ![]() . Ответ. 0,4
. Ответ. 0,4
3. Найдите ![]() , если
, если ![]() . Ответ. -12,88
. Ответ. -12,88
4. Найдите ![]() , если
, если ![]() . Ответ. -0,84
. Ответ. -0,84
5. Найдите значение выражения: ![]() . Ответ. 6
. Ответ. 6
6. Найдите значение выражения ![]() . Ответ. -19
. Ответ. -19
1.2. Задания на упрощение тригонометрических выражений.
Формулы приведения должны быть хорошо усвоены учащимися, так как они найдут дальнейшее применение на уроках геометрии, физики и других смежных дисциплин.
Пример 5. Упростите выражения 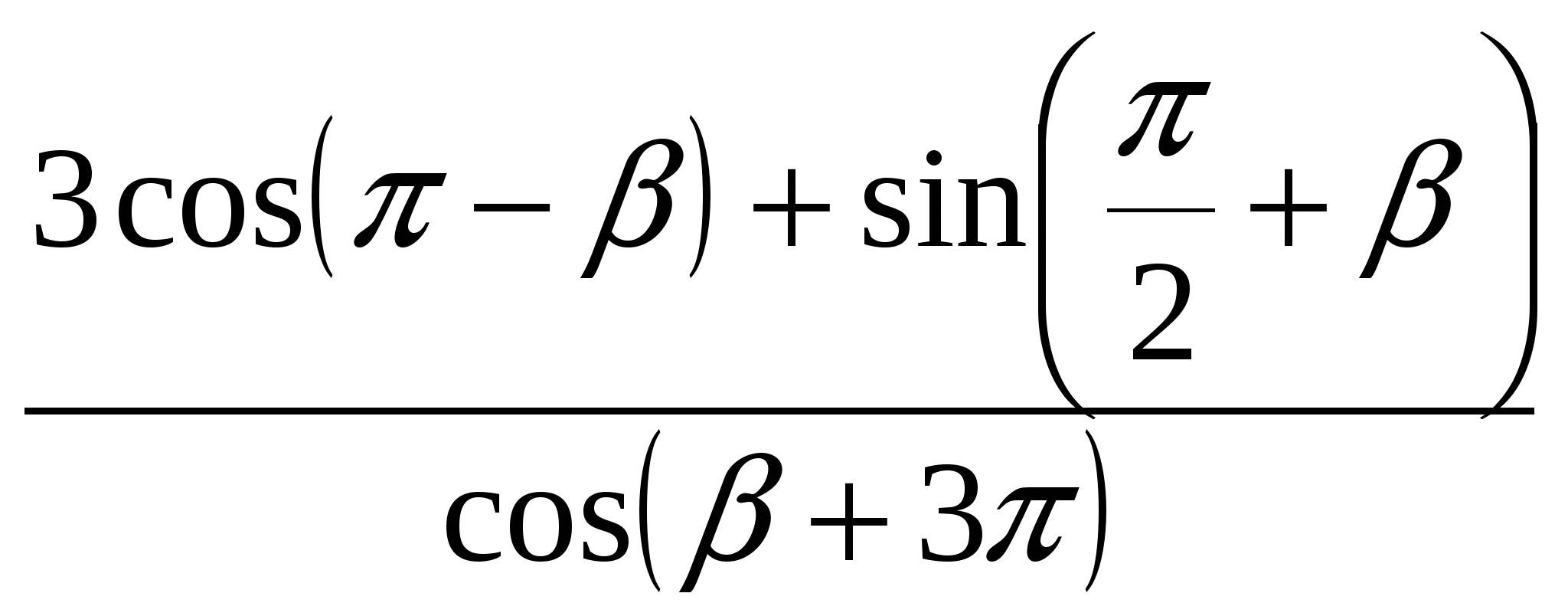 .
.
Решение. 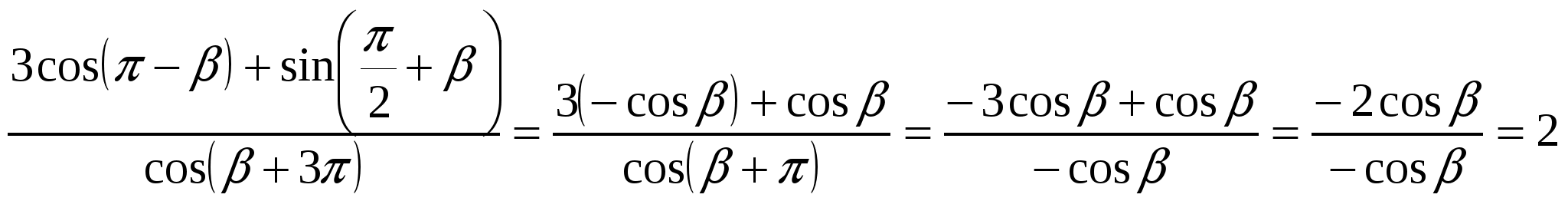 .
.
Ответ. 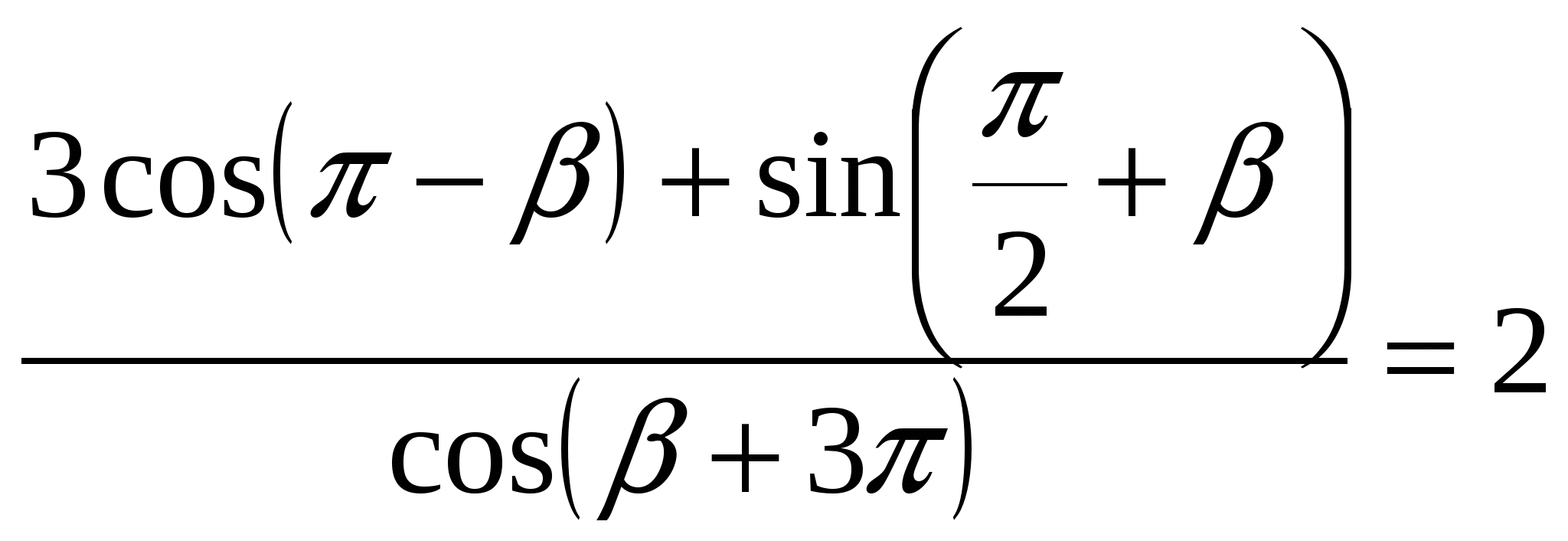 .
.
Задания для самостоятельного решения:
1. Упростите выражение 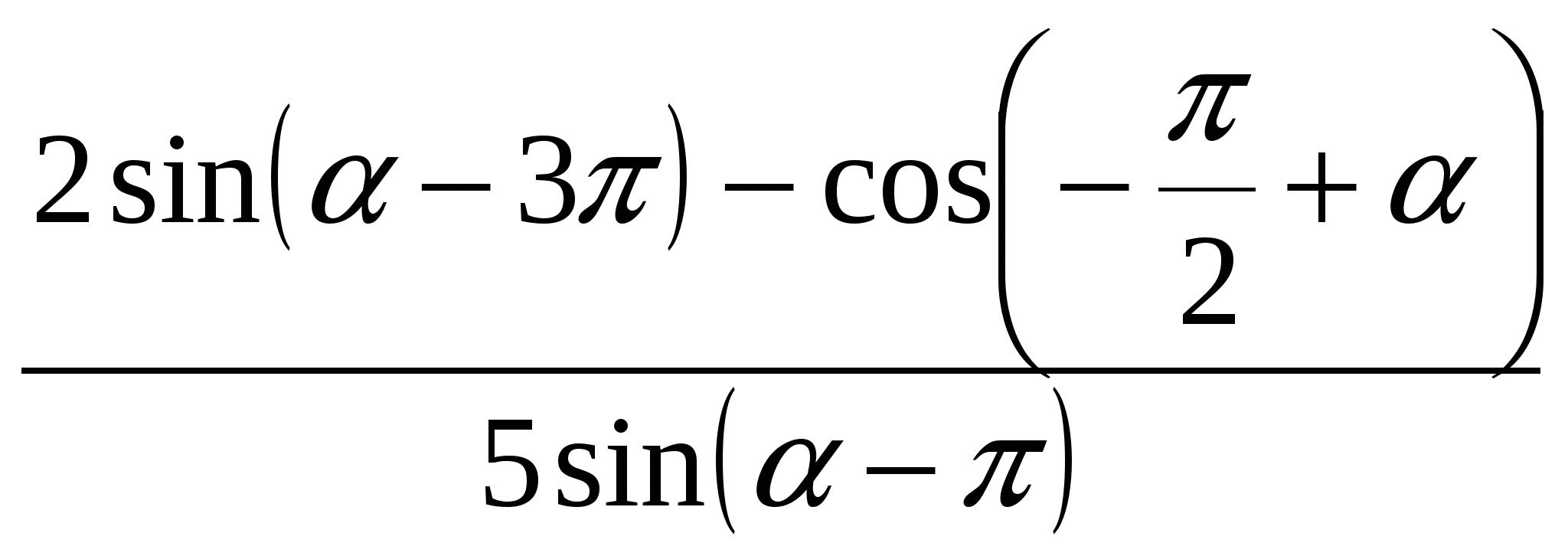 . Ответ. 0,6
. Ответ. 0,6
2. Найдите ![]() , если
, если ![]() и
и ![]() . Ответ. 10,56
. Ответ. 10,56
3. Найдите значение выражения ![]() , если
, если ![]() . Ответ. 2
. Ответ. 2
1.3. Задания на преобразование числовых тригонометрических выражений.
При отработке умений и навыков заданий на преобразование числовых тригонометрических выражений, следует обратить внимание на знание таблицы значений тригонометрических функций, свойств четности и периодичности тригонометрических функций.
а) Использование точных значений тригонометрических функций для некоторых углов.
Пример 6. Вычислите ![]() .
.
Решение. ![]() .
.
Ответ. ![]() .
.
б) Использование свойств четности тригонометрических функций.
Пример 7. Вычислите ![]() .
.
Решение. ![]() .
.
Ответ. ![]()
в) Использование свойств периодичности тригонометрических функций.
Пример 8. Найдите значение выражения 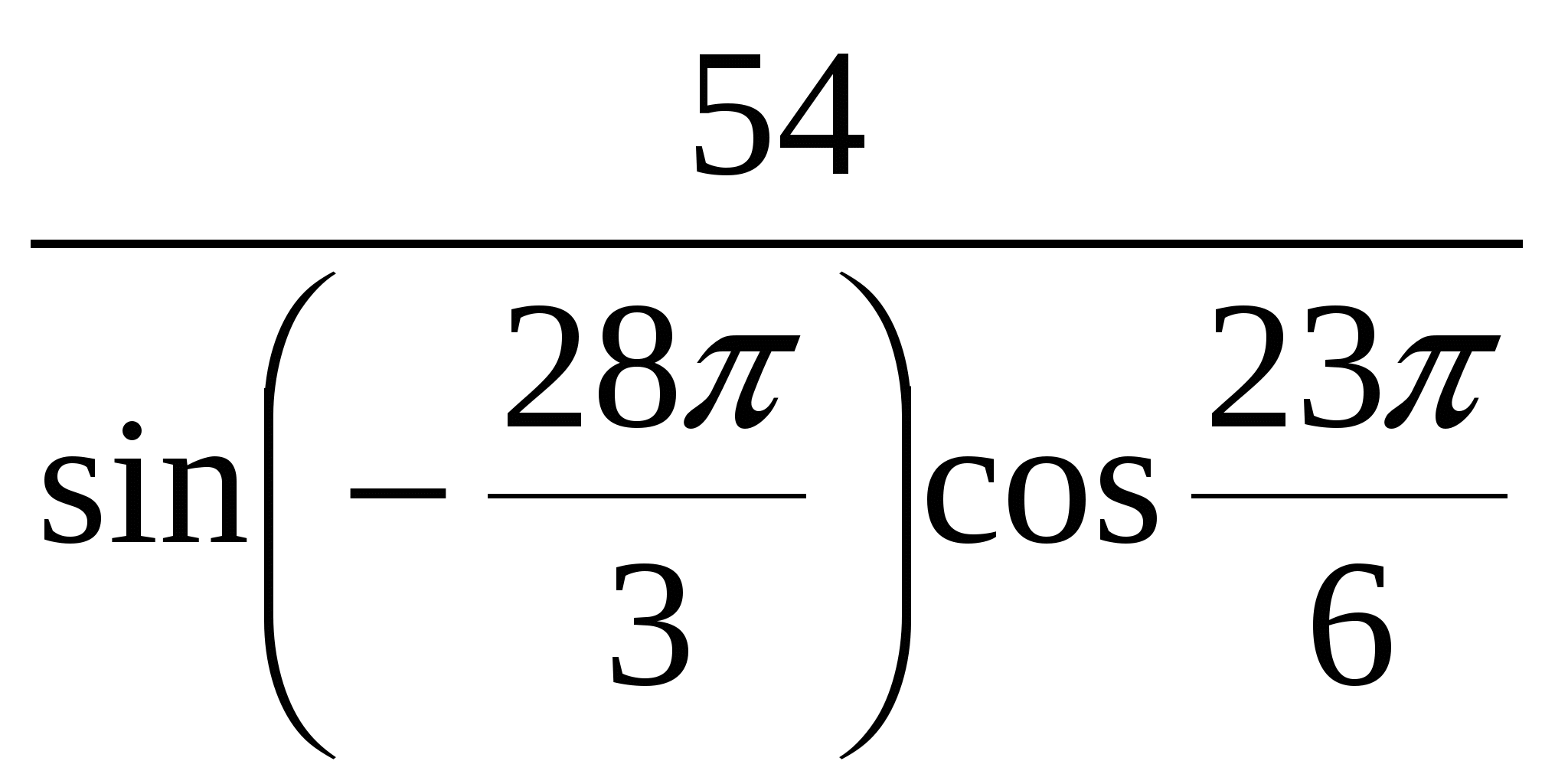 .
.
Решение. 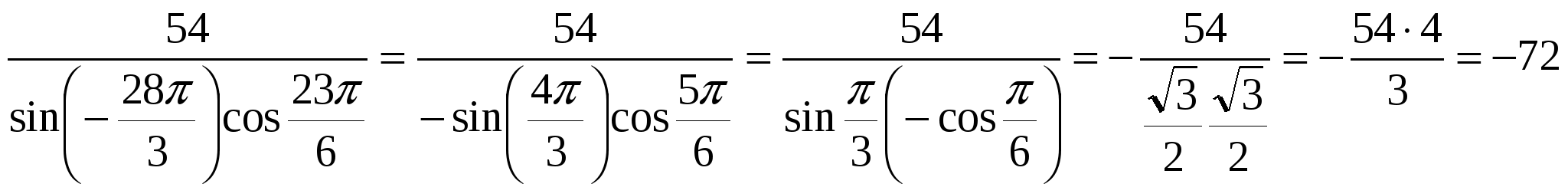 .
.
Ответ. 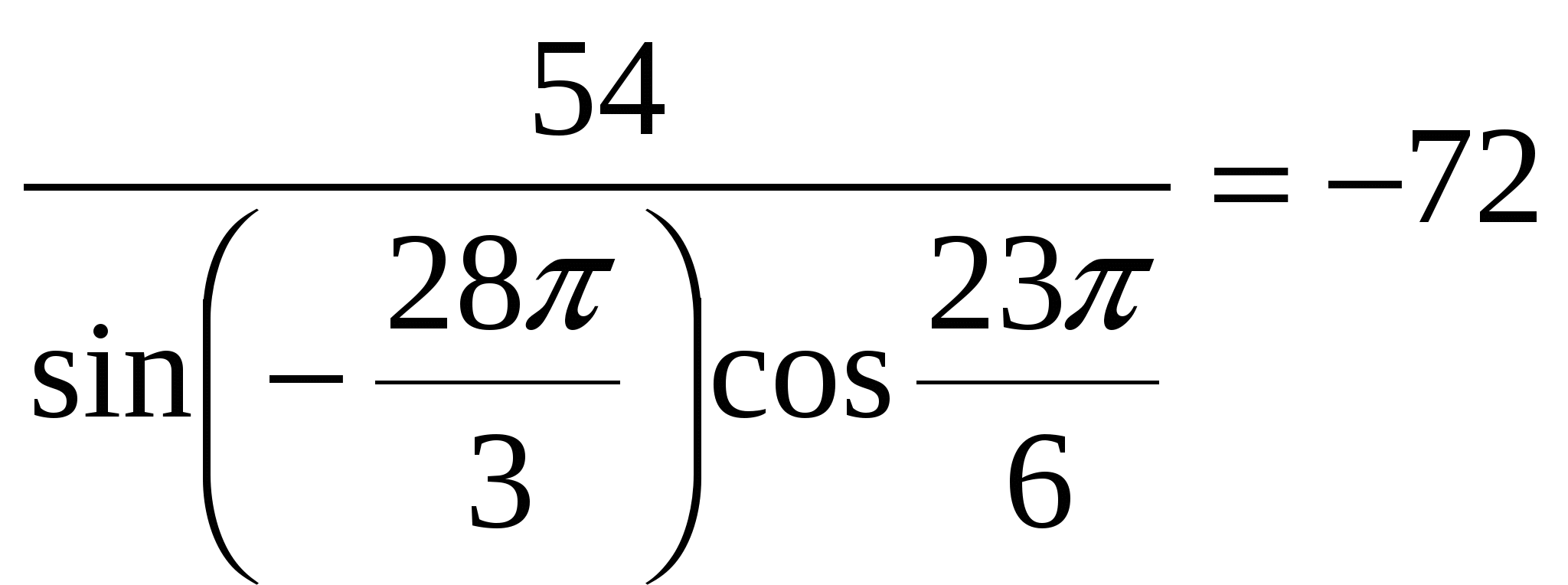 .
.
Задания для самостоятельного решения:
1. Найдите значение выражения ![]() . Ответ. -40,5
. Ответ. -40,5
2. Найдите значение выражения ![]() . Ответ. 17
. Ответ. 17
3. Найдите значение выражения ![]() . Ответ. 6
. Ответ. 6
4. Найдите значение выражения ![]() . Ответ. -24
. Ответ. -24
5. Найдите значение выражения 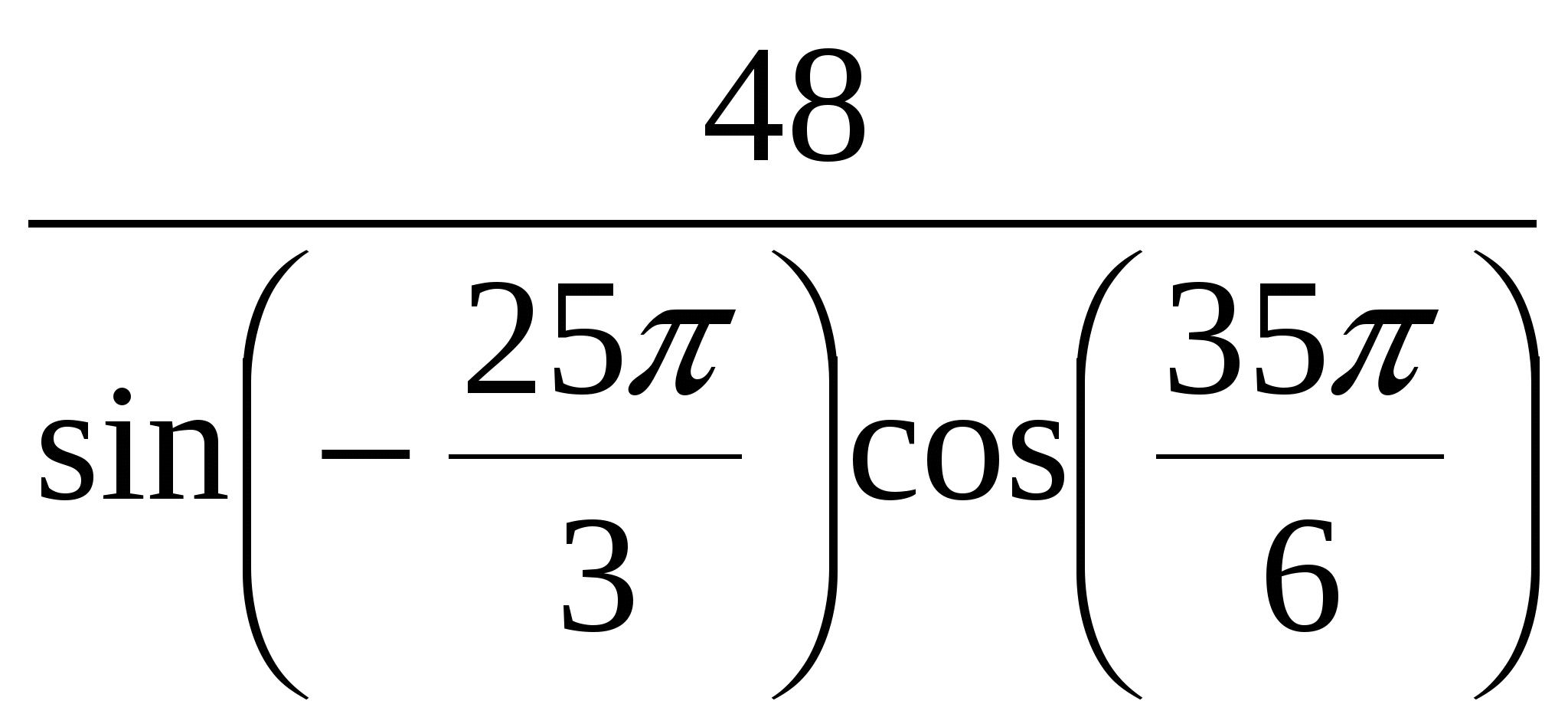 Ответ. -64
Ответ. -64
1.4 Задания смешанного типа.
Тестовая форма аттестации обладает весьма существенными особенностями, поэтому важно обращать внимание на задания связанные с применением нескольких тригонометрических формул одновременно.
Пример 9. Найдите ![]() , если
, если ![]() .
.
Решение. 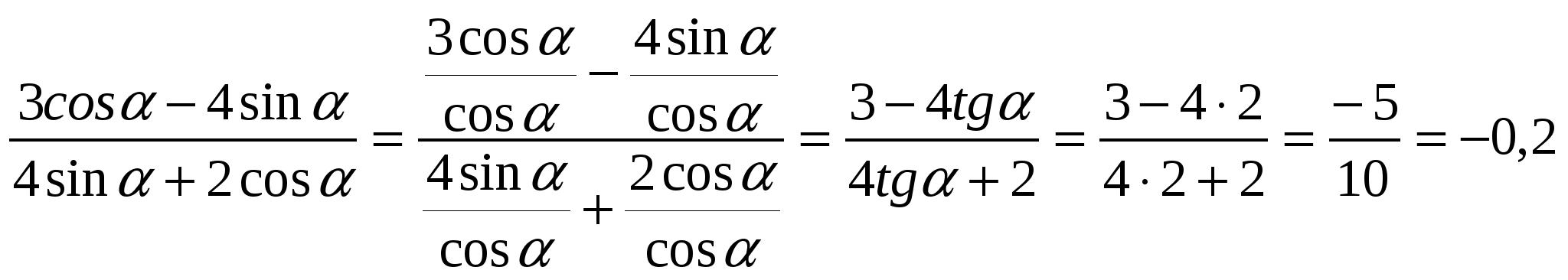 .
.
Ответ. ![]() .
.
Пример 10. Найдите ![]() , если
, если ![]() и
и ![]() .
.
Решение. ![]() .
.
![]() .
.
Т.к. ![]() , то
, то ![]() .
.
![]() .
.
Ответ. ![]() .
.
Пример 11. Найдите ![]() , если
, если ![]() .
.
Решение. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Ответ. ![]()
Пример 12. Вычислите ![]() .
.
Решение. ![]() .
.
Ответ. ![]() .
.
Пример 13. Найдите значение выражения ![]() , если
, если ![]() .
.
Решение. ![]() .
.
Ответ. ![]() .
.
Задания для самостоятельного решения:
1. Найдите ![]() , если
, если ![]() . Ответ. -1,75
. Ответ. -1,75
2. Найдите ![]() , если
, если ![]() . Ответ. 3
. Ответ. 3
3. Найдите ![]() , если
, если ![]() . Ответ. 0.25
. Ответ. 0.25
4. Найдите значение выражения ![]() , если
, если ![]() . Ответ. 0,3
. Ответ. 0,3
5. Найдите значение выражения ![]() , если
, если ![]() . Ответ. 5
. Ответ. 5
Глава 2. Методические аспекты организация итогового повторения темы «Преобразование тригонометрических выражений».
Одним из важнейших вопросов, способствующих дальнейшему повышению успеваемости, достижению глубоких и прочных знаний у учеников является вопрос о повторении ранее пройденного материала. Практика показывает, что в 10 классе целесообразней организовать тематическое повторение; в 11 классе - итоговое повторение.
2.1. Тематическое повторение в 10 классе.
В процессе работы над математическим материалом особенно большое значение приобретает повторение каждой законченной темы или целого раздела курса.
При тематическом повторении систематизируются знания учащихся по теме на завершающем этапе ее прохождения или после некоторого перерыва.
Для тематического повторения выделяются специальные уроки, на которых концентрируется и обобщается материал одной какой-нибудь темы.
Повторение на уроке проводится путём беседы с широким вовлечением учащихся в эту беседу. После этого учащиеся получают задание повторить определённую тему и предупреждаются, что будет проведена зачетная работа по тестам.
Тест по теме должен включать все ее основные вопросы. После выполнения работы проводится разбор характерных ошибок и организуется повторение для их устранения.
Для уроков тематического повторения нами предлагаются разработанные зачетные работы в виде тестов по теме «Преобразование тригонометрических выражений».
Тест № 1
№
Задание
Найдите ![]() , если
, если ![]() и
и ![]() .
.
Найдите ![]() , если
, если ![]()
![]() .
.
Найдите ![]() , если
, если ![]() .
.
Найдите значение выражения 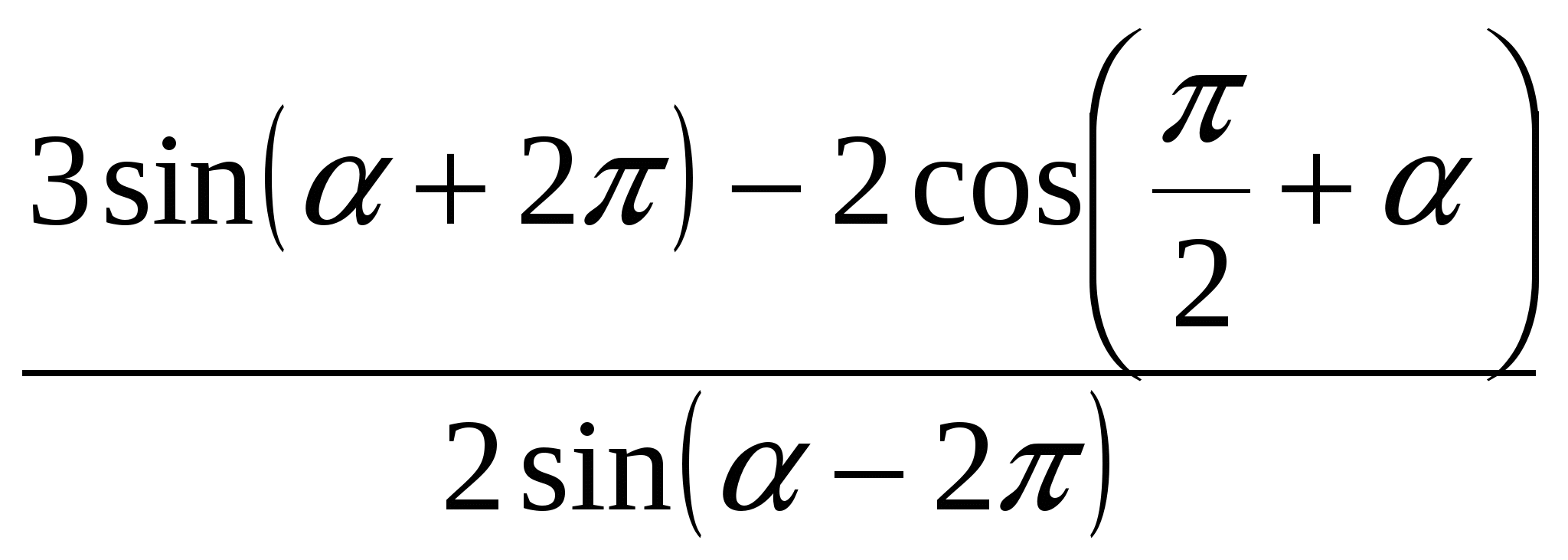 .
.
Найдите ![]() , если
, если ![]() .
.
Найдите значение выражения ![]() .
.
Найдите значение выражения ![]() .
.
Найдите значение выражения 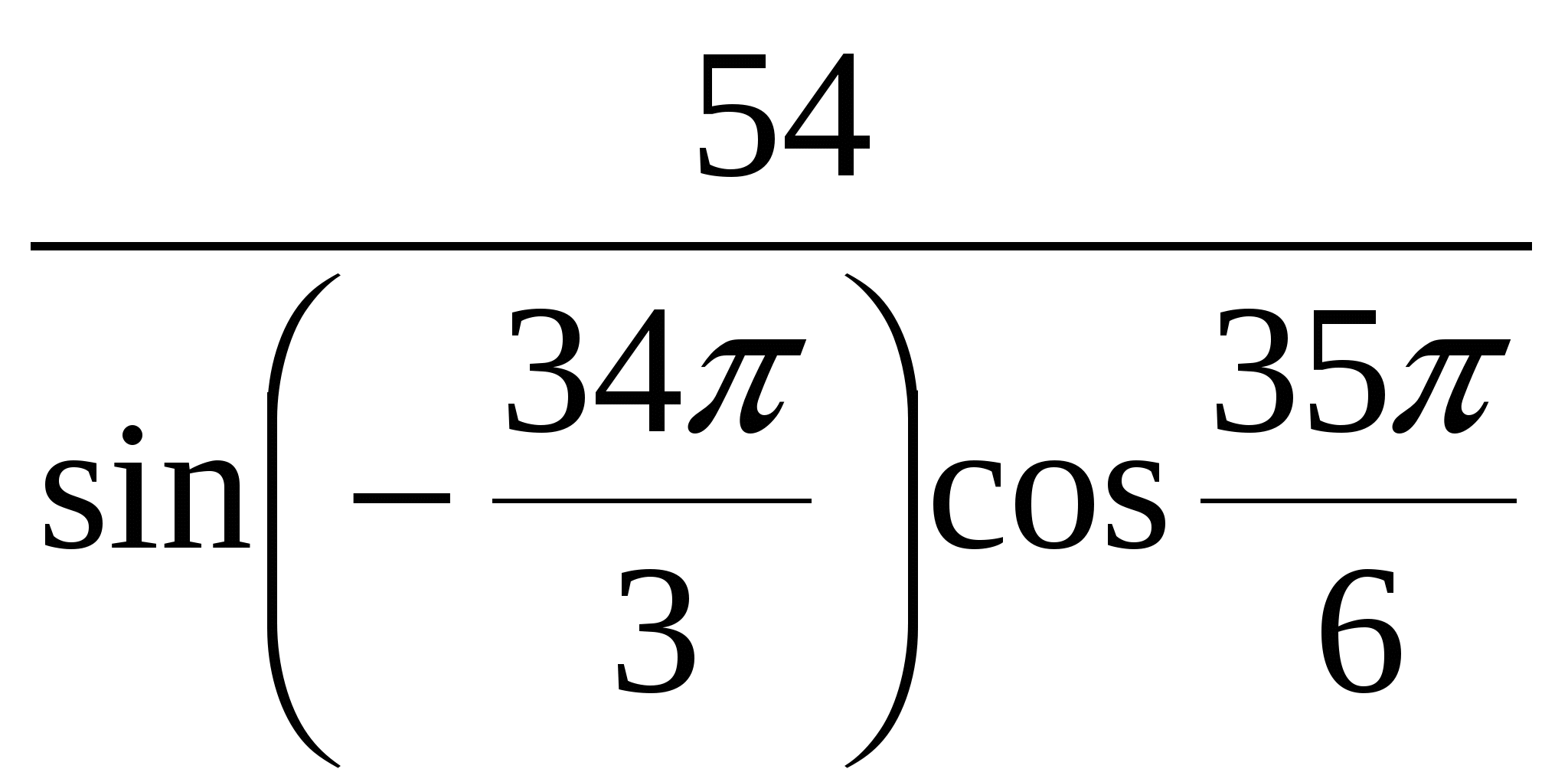 .
.
Найдите ![]() , если
, если ![]() .
.
Найдите значение выражения ![]() , если
, если ![]() .
.
Тест № 2
№
Задание
Найдите ![]() если
если ![]() и
и ![]() .
.
Найдите ![]() , если
, если ![]()
![]() .
.
Найдите ![]() , если
, если ![]() .
.
Найдите значение выражения 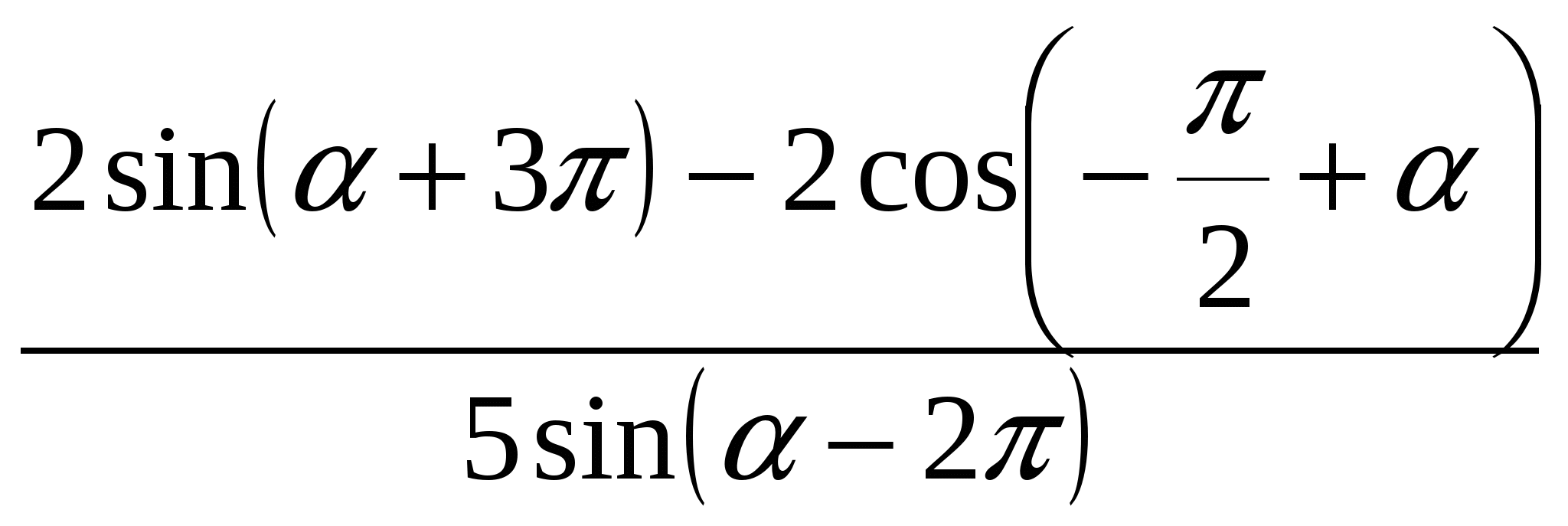 .
.
Найдите ![]() , если
, если ![]() .
.
Найдите значение выражения ![]() .
.
Найдите значение выражения ![]() .
.
Найдите значение выражения 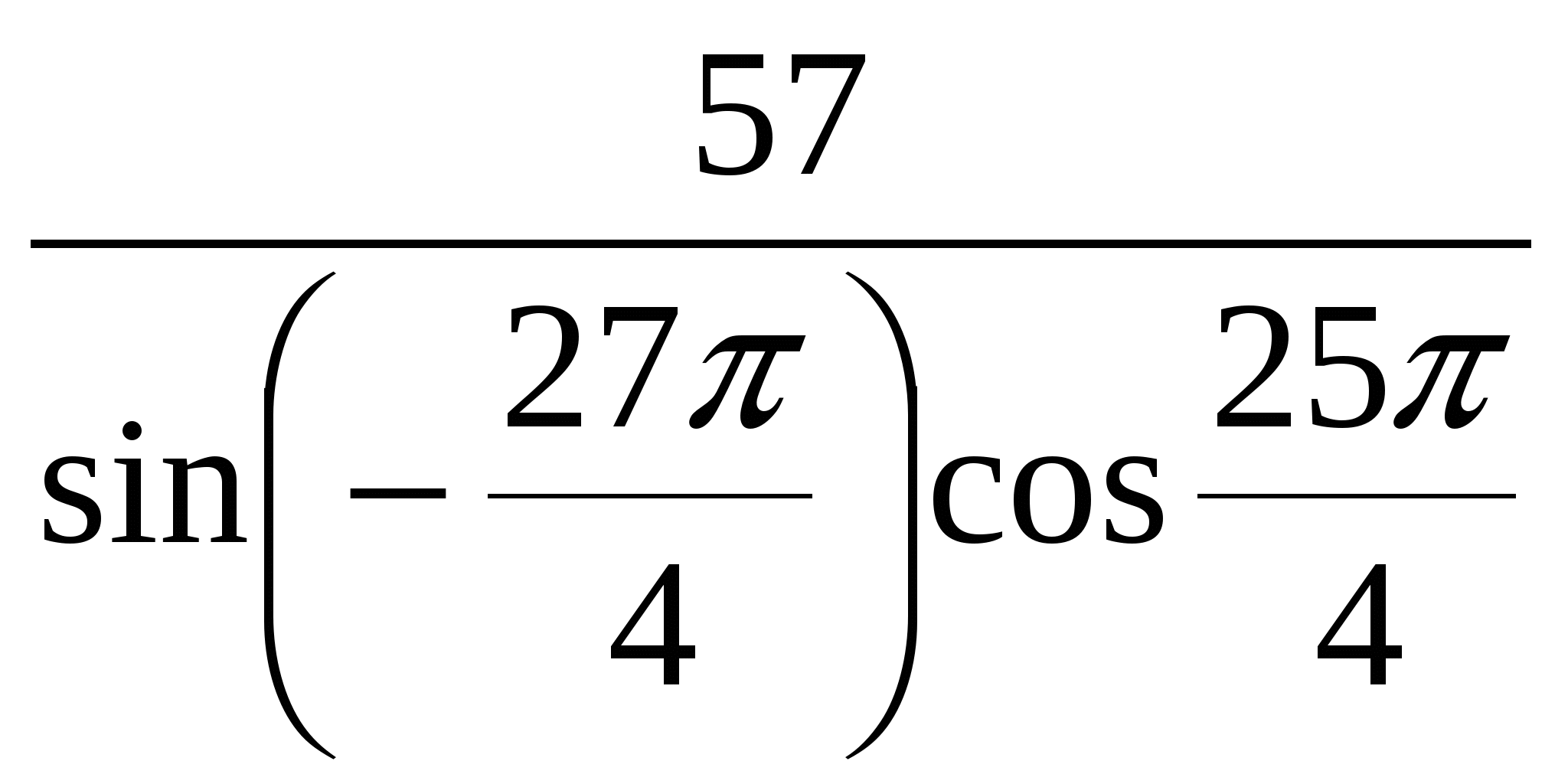 .
.
Найдите ![]() , если
, если ![]() .
.
Найдите значение выражения ![]() , если
, если ![]() .
.
Тест № 3
№
Задание
Найдите ![]() если
если ![]() и
и ![]() .
.
Найдите ![]() , если
, если ![]()
![]() .
.
Найдите ![]() , если
, если ![]() .
.
Найдите значение выражения 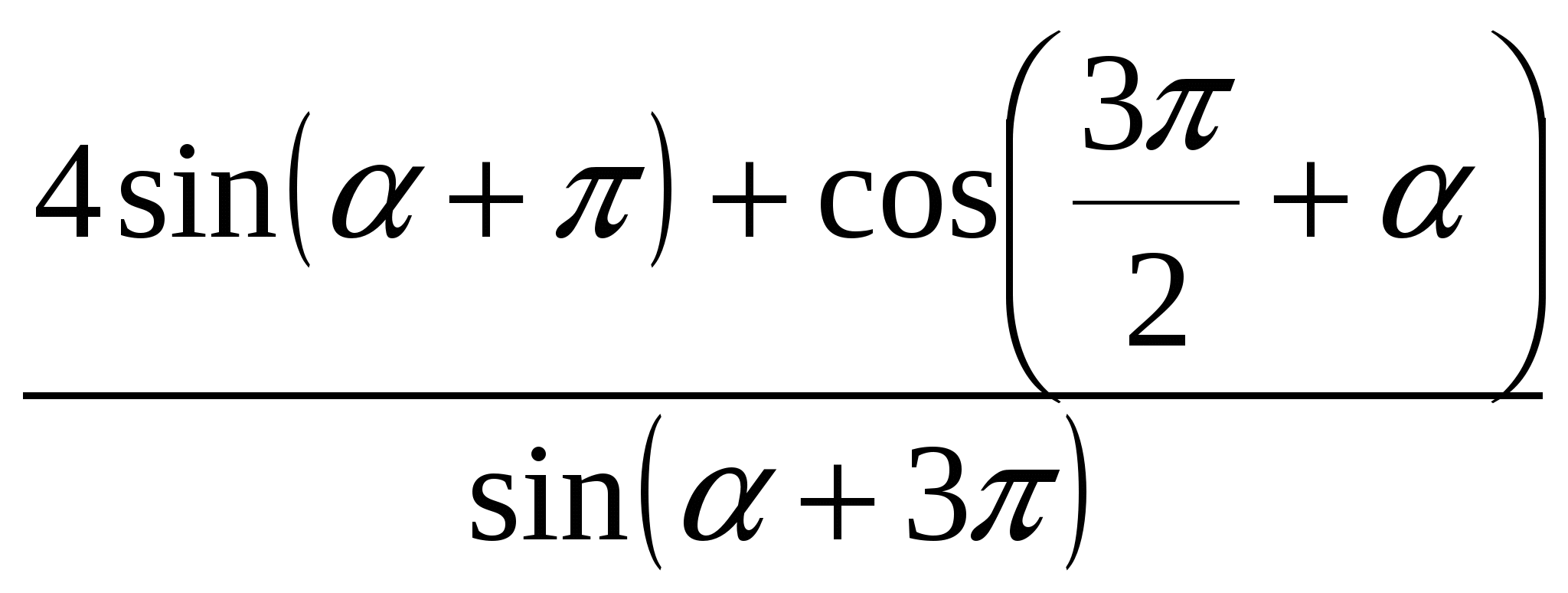 .
.
Найдите ![]() , если
, если ![]() .
.
Найдите значение выражения ![]() .
.
Найдите значение выражения ![]() .
.
Найдите значение выражения 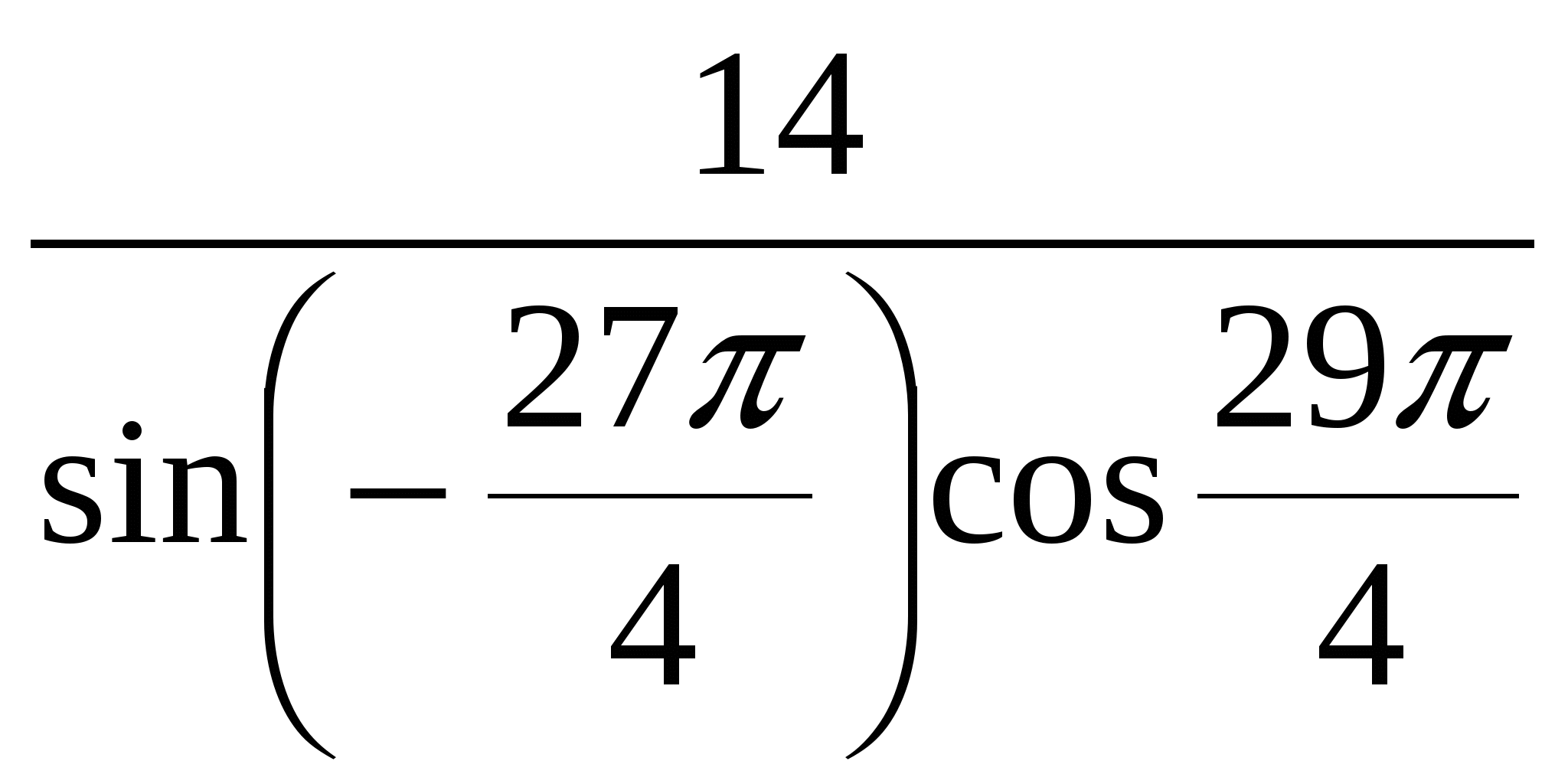 .
.
Найдите ![]() , если
, если ![]() .
.
Найдите значение выражения ![]() , если
, если ![]() .
.
Таблица ответов
Тест
1
2
3
4
5
6
7
8
9
10
№ 1
-0,2
2,5
-0,12
2,5
-0,25
-15
20
72
-0,1
-0,1
№ 2
0,5
-1
-0,16
-0,8
-20
-6
40
-114
-1,5
-0,7
№ 3
0,9
0,6
-0,12
3
-2
-48
63
28
-0,8
2,1
2.2. Итоговое повторение в 11 классе.
Итоговое повторение проводится на завершающем этапе изучения основных вопросов курса математики и осуществляется в логической связи с изучением учебного материала по данному разделу или курсу в целом.
Итоговое повторение учебного материала преследует цели:
1. Активизация материала всего учебного курса для прояснения его логической структуры и выстраивания системы внутри предметных и меж предметных связей.
2. Углубление и по возможности расширение знаний учащихся по основным вопросам курса в процессе повторения.
В условиях обязательной для всех выпускников сдачи экзамена по математике, постепенное введение ЕГЭ заставляет учителя по-новому подходить к подготовке и проведению уроков, учитывая необходимость обеспечить овладение всеми школьниками учебного материала на базовом уровне, а также возможность мотивированным учащимся, заинтересованным в получении высоких баллов для поступления в вуз, динамичного продвижения в овладении материалом на повышенном и высоком уровне.
На уроках итогового повторения можно рассмотреть следующие задания:
Пример 1. Вычислите значение выражения ![]() .
.
Решение. ![]() =
= ![]() = =
= = ![]() =
=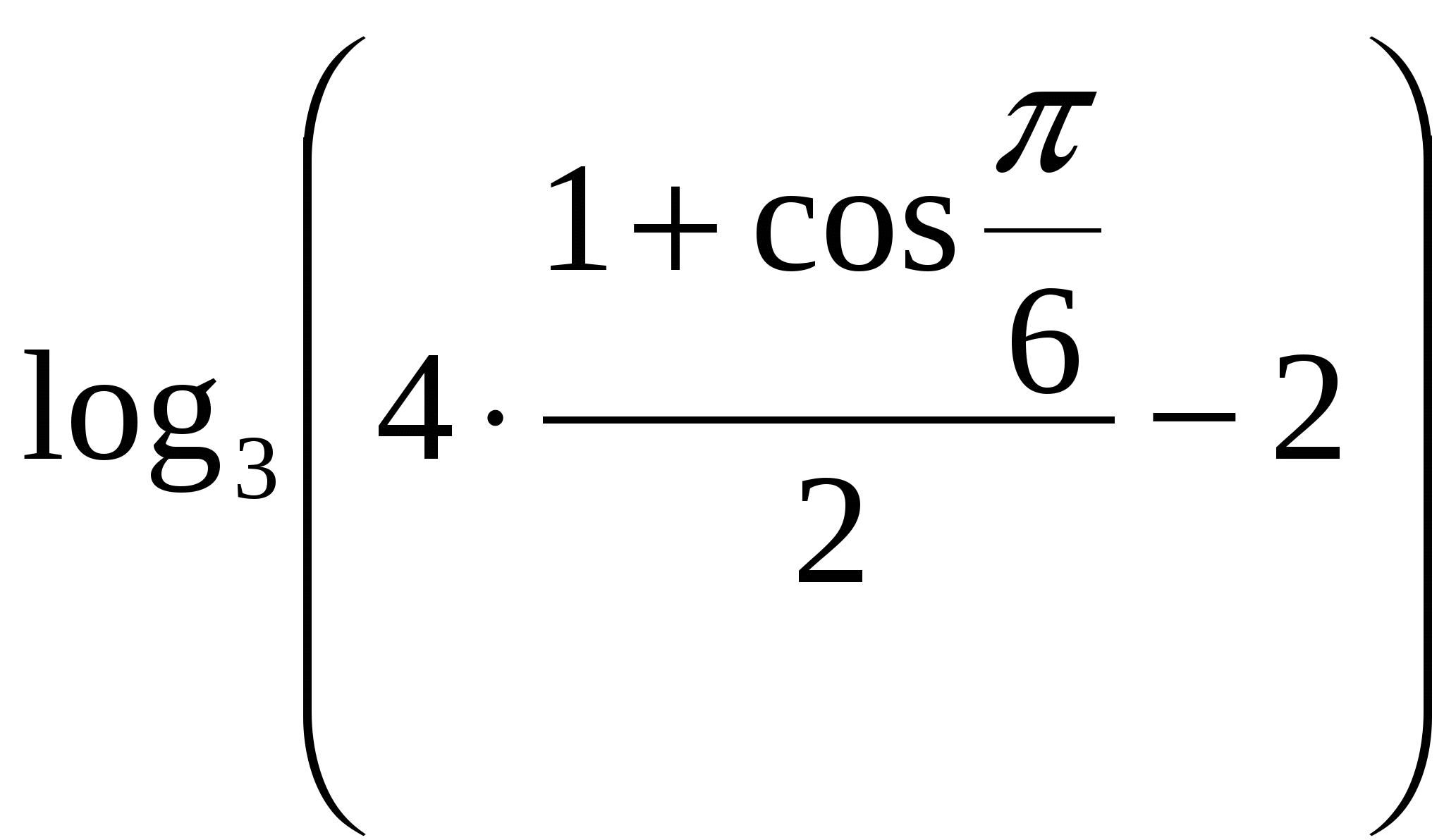 =
=![]() =
=![]() =0,5.
=0,5.
Ответ. 0,5.
Пример 2. Укажите наибольшее целое значение, которое может принимать выражение ![]() .
.
Решение. Так как ![]() может принимать любое значение, принадлежащее отрезку [–1; 1], то
может принимать любое значение, принадлежащее отрезку [–1; 1], то ![]() принимает любое значение отрезка [–0,4; 0,4], поэтому
принимает любое значение отрезка [–0,4; 0,4], поэтому ![]() . Целое значение выражения одно – число 4.
. Целое значение выражения одно – число 4.
Ответ: 4
Пример 3. Упростите выражение ![]() .
.
Решение: Воспользуемся формулой разложения на множители суммы кубов: ![]() . Имеем
. Имеем ![]()
![]() .
.
Имеем: ![]() .
.
Ответ : 1
Пример 4. Вычислите ![]() .
.
Решение. ![]() .
.
Ответ: 0,28
Для уроков итогового повторения нами предлагаются разработанные тесты по теме «Преобразование тригонометрических выражений».
Тест № 1
№
Задание
Найти значение выражения ![]() .
.
Вычислите ![]() , при
, при ![]() .
.
Вычислите ![]() .
.
Найти значение выражения ![]() .
.
Найдите наибольшее значение функции ![]() на промежутке
на промежутке ![]() .
.
Вычислите ![]() .
.
Тест № 2
№
Задание
Упростите ![]() .
.
Укажите наибольшее целое число, не превосходящее ![]() .
.
Вычислите ![]() .
.
Найти значение выражения ![]() .
.
Найдите наименьшее значение функции ![]() .
.
Вычислите ![]() .
.
Тест № 3
№
Задание
Упростите ![]() .
.
Сколько натуральных чисел входит в множество значений функции![]() .
.![]()
![]()
![]()
Дано ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Найти
. Найти ![]() .
.
Найти значение выражения ![]() .
.
Найти значение выражения ![]() .
.
Вычислите ![]() .
.
Таблица ответов
Тест
1
2
3
4
5
6
№ 1
0,29
-1,5
0,25
0
0,5
1,5
№ 2
1
0
2
0
-2
-1
№ 3
0
1
0,28
0
1
6
Заключение.
Проработав соответствующую методическую литературу по данной теме, можно сделать вывод о том, что умение и навыки решать задания, связанные с тригонометрическими преобразованиями в школьном курсе математики является очень важным.
В ходе проделанной работы проведена классификация заданий В7. Рассмотрены тригонометрические формулы наиболее часто применяемые в КИМах 2012 года. Приведены примеры заданий с решениями. Разработаны дифференцируемые тесты для организации повторения и систематизации знаний в рамках подготовки к ЕГЭ.
Целесообразно продолжить начатую работу, рассмотрев решение простейших тригонометрических уравнений в задании В5, исследование тригонометрических функций в задании В14, задания В12, в которых имеются формулы, описывающие физические явления и содержащие тригонометрические функции.
В заключение хотелось бы заметить, результативность сдачи ЕГЭ во многом определяется тем, насколько эффективно организован процесс подготовки на всех ступенях обучения, со всеми категориями обучающихся. А если мы сумеем сформировать у обучающихся самостоятельность, ответственность и готовность к продолжению обучения в течение всей последующей жизни, то мы не только выполним заказ государства и общества, но и повысим собственную самооценку.
Повторение учебного материала требует от учителя творческой работы. Он должен обеспечить четкую связь между видами повторения, осуществить глубоко продуманную систему повторения. Овладеть искусством организации повторения - такова задача учителя. От ее решения во многом зависит прочность знаний учащихся.
Литература.
Выгодский Я.Я., Справочник по элементарной математике. -М.: Наука, 1970.
Задачи повышенной трудности по алгебре и началам анализа : Учебное пособие для 10-11 классов средней школы / Б.М. Ивлев, А.М. Абрамов, Ю.П. Дудницын, С.И. Шварцбурд. – М.: Просвещение, 1990.
Караваева Л.А. Применение основных тригонометрических формул к преобразованию выражений (10-й класс) //Фестиваль педагогических идей. 2012-2013.
Корянов А.Г. , Прокофьев А.А. Готовим к ЕГЭ хорошистов и отличников. — М.: Педагогический университет «Первое сентября», 2012.- 103 с.
Кузнецова Э.Н. Упрощение тригонометрических выражений. Решение тригонометрических уравнений различными методами (подготовка к ЕГЭ). 11-й класс. 2012-2013.
Куланин Е. Д. 3000 конкурсных задач по математике. 4-е ихд., испр. и доп. – М.: Рольф, 2000.
Мордкович А.Г. Методические проблемы изучения тригонометрии в общеобразовательной школе // Математика в школе. 2002. №6.
Пичурин Л.Ф. О тригонометрии и не только о ней: -М. Просвещение, 1985г.
Решетников Н.Н. Тригонометрия в школе: -М. : Педагогический университет «Первое сентября», 2006, лк 1.
Шабунин М.И., Прокофьев А.А. Математика. Алгебра. Начала математического анализа. Профильный уровень: учебник для 10 класса — М.: БИНОМ. Лаборатория знаний, 2007.
Образовательный портал для подготовки к ЕГЭ. http://reshuege.ru/test?theme=59
Образовательный портал для подготовки к ЕГЭ. http://xn--c1ada6bq3a2b.xn--p1ai/test?theme=167
Подготовка к ЕГЭ по математике "Ох, уж эта тригонометрия! http://festival.1september.ru/articles/621971/
Проект "Математика? Легко!!!" http://matematikalegko.ru/zadachi-b7/preobrazovanie-chislovyx trigonometricheskix-vyrazhenij-2-sposoba.html
Сайт рефератов http://podelise.ru/docs/index-292781.html
Сайт учебного характера http://rudocs.exdat.com/docs/index-15408.html
Учебный центр по подготовке к ГИА и ЕГЭ http://www.resolventa.ru/

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ