Конспект урока по Алгебре "Квадратичная функция. Построение графика квадратичной функции" 8 класс
























 Конспект урока
Конспект урока
Тема урока: Квадратичная функция. Построение графика квадратичной функции .
Класс: 8
Цели урока:
1. Формирование общекультурной компетенции.
Аспекты: а) умение ставить цель; б) находить пути ее достижения; в) оценивать результаты деятельности.
2. Формирование учебно-познавательной компетенции.
Аспекты: а) знание основных понятий, входящих в тему;
б) выработка умений работать самостоятельно с теоретическим материалом на уровне анализа и вычленения главного; в) умение строить график функции y = ax² + bx + c.
3. Формирование коммуникативной компетенции:
Аспекты: а) развивать умения работать в группе; б) формировать чувство уважения к мнению окружающих.
4. Формирование информационной компетенции.
Аспекты: а) извлечение первичной информации, её обработка, представление и передача; б) превращение информации в знание.
Задачи урока:
Образовательные:
- формировать навыки построения графика функции в ходе урока и самостоятельной работе;
- развивать умения и навыки учащихся работать самостоятельно с теоретическим и практическим материалом на уровне анализа и вычленения главного.
Развивающие:
- формировать информационно – коммуникативные умения (добывать, обрабатывать, формировать информацию);
- развивать критическое мышление;
- развивать познавательную активность.
Воспитательные:
- содействовать расширению кругозора;
- развивать: самостоятельность и творчество, чувство ответственности, толерантности; умения общаться и работать в команде, аргументировано отстаивать свои взгляды.
Результаты обучения:
- Личностные:
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
умение контролировать процесс и результат учебной математической деятельности.
- Метапредметные:
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.
- Предметные:
уметь оперировать понятиями темы «Функция y = ax² + bx + c, её свойства и график»;
уметь строить график функции;
Тип урока: урок повторения и систематизации знаний
Применяемые методы и педтехнологии: групповая технология, проблемно-диалогическая технология с использованием стратегий смыслового чтения, личностно-ориентированная.
Методы: проблемно-поисковый, наглядные, дедуктивные, продуктивные, практические.
Приёмы: работа в парах, обсуждение, обобщение знаний.
Формы работы на уроке: фронтальная, самостоятельная, групповая, индивидуальная.
Используемые средства обучения: карточки-заготовки для построения графика функции, листы контроля, источник интернетресурса, карточки с заданиями .
Необходимое оборудование и материалы: компьютер, проектор, экран.
Сопровождение к уроку: компьютерная презентация (Приложение 1).
Время урока: 45 минут
Структура урока:
Организационный этап – 1,5 мин.
Постановка проблемы -3,5 мин
Актуализация знаний –14 минут
Физкультминутка – 1 минута.
Исследование – 20 мин.
6. Самостоятельная работа с самопроверкой по эталону – 7 мин.
Подведение итогов урока – 3 минуты.
Домашнее задание – 1 мин.
Рефлексия – 3 мин
Ход урока:
1.Организационный этап. ( вначале урока раздаются оценочные листы каждому учащему. Учитель объясняет ,что каждое задание ученик оценивает по критериям и отмечает в оценочном листе . класс разделен на группы по 5-6 человек)Слайд №4.
Слайд №2. Запишите, пожалуйста, в тетрадях тему урока и число. каждый
2. Постановка проблемы Слайд №4
ПРИМЕНЕНИЕ ФУНКЦИИ ВОКРУГ НАС.
Видео ссылка http://www.youtube.com/watch?v=6fCB_mmpMVo .
3. Актуализация знаний
a)Вопросы по теме квадратичная функция группа др. группе.
b)Лист № 1. Вставить пропущенные слова вместо многоточия. Время работы 2-3 мин. (Каждой группе по одному листу)
Лист № 1.
Вместо многоточия вставить пропущенные слова.
Функция вида y = ax² + bx + c, где a, b и c заданные … числа, … ≠ 0,
x - … переменная, называется … функцией.
Функция y = x² - это … функция y = ax² + b… + c, при a = …, b = …, c = ….
Значения x, при которых квадратичная функция y (x) = 0, называются … этой функции.
Кривая, являющаяся графиком функции y = x², называется … .
Парабола y = x² касается оси ОХ в точке с координатами ( …; …).
График функции y = x² симметричен относительно оси … .
Ось ОУ является осью … параболы.
Точку пересечения параболы с её осью … называют … … .
Функция y = x² является … на промежутке x ≥ 0 и убывающей на промежутке x…0 .
При a … 0 ветви параболы y = ax² + bx + c направлены вверх, а при a … 0 - вниз.
Координаты вершины параболы y = ax² + bx + c можно найти по формулам:
x0 = - ― , y0 = y(x0) = a … + b … + c.
Работа в паре. Лист № 2 (1 и 2 задание). Время работы 3 – 4 мин.
Лист № 2.
Ответьте на вопросы.
Какая функция:
а) является квадратичной,
б) назовите коэффициенты a, b, c у квадратичных функций;
в) определите направление ветвей параболы:
y = 2x² + x + 3;
y = 5x + 1;
y = 4x²;
y = 3x² - 1;
y = x³ + 7x - 1;
y = -3x² + 2x;
y = 6x³ - 5x² + 4x + 9;
y = 2х4.
Найти координаты вершины параболы:
у = (x-3)²-2;
у = (x+2)²-7;
у = (x+4)²+3;
у = -4(x-1)²+5;
y = x²+4x+1;
у = 2х2 – 6х + 11;
у = х2 – 6х – 7;
у = х2 + 3;
у = - х2 – 5;
у = 3х2 – 2х.
(3;-2)
(-2;-7)
(-4;3)
(1;5)
(-1;-2)
(1,5; 6,5)
(1,5; 13,75)
(0;3)
(0;-5)
(1/3; -1/3)
Лист № 2 (3 и 4 задание). Фронтальная работа с классом. Слайд №7-8
По графику данной функции назовите её свойства:
У
О
-1 1 3 Х
-2 О/
Восстановите схему построения графика квадратичной функции.
Построить вершину параболы О/ (х0; у0) по формулам х0 = , у0 = у (х0). Найти нули функции, если они есть, и построить на оси ОХ соответствующие точки. Провести через построенные точки параболу.
Провести через вершину параболы прямую, параллельную оси ОУ, - ось симметрии параболы
Построить две какие-нибудь точки параболы (х - берём произвольно, у - считаем, подставляя в функцию).
4. Физкультминутка – 1 минута. Слайд №7
5. Исследование Работа в группе.
a)Слайд №8 видео по http://www.youtube.com/watch?v=0xfTl3Ugyjk
По этому видео у групп образовались вопросы. На планшетах ищут ответы, обсуждая в группе, и находя в интернете.
(отражатели карманных фонариков, автомобильных фар, прожекторов, «тарелки» спутникового телевидения и связи имеют форму параболоида.Расчитайте, по правилам геометрической оптики, в каком месте параболоида должен находиться источник излучения, чтобы лучи из этого параболоида выходили параллельно оптической оси. Разумеется, при обратном ходе параллельные лучи должны сходиться в одну точку, называемую фокусом параболоида. Расчёт на рисунке приведён.)
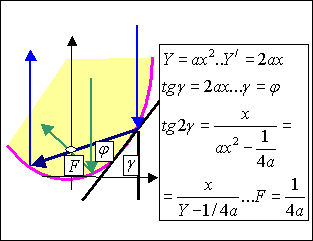
6.Самостоятельная работа. Построение графика квадратичной функции. (задания по уровням) учащимся раздаются карточки.
Оценка «3»
Построить график функции:
у= х2.
Памятка в помощь.
1.Для построения графика функции у = х2 сначала заполните таблицу:
-
Х
-3
-2
-1
0
1
2
3
У
9
2.Отметьте в координатной плоскости точки, координаты которых указаны в таблице.
3.Соедините эти точки плавной линией
Оценка «4»
Построить график функции:
у = х2 – 4х – 5.
Дополнительно: опишите основные свойства функции.
Оценка «5»
Исследовать (описать) свойства функции по графику.
У
О/
5
4
Х
-2
О
1
2
Дополнительное задание для оценки «3».
Укажите область определения функции.
Укажите координаты вершины параболы.
Найти наименьшее значение у.
Дополнительное задание для оценки «5
Найти координаты точек пересечения параболы с осями координат:
у = - 2х2 – 8х + 10.
Оценка «4»: вершина (2; -9), нули: х = - 1 и х = 5
7. Подведение итогов урока . по оценочному листу учащиеся считают
Задание
Отметка
Устные вопросы
за работу в группе
Работа в парах
Исследование
Построение графика функции (сам. Работа
Итого
Слайд №9-10
8. Домашнее задание. Слайд №11
9 .Рефлексия. Слайд №12 ( пишут на стикерах)

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ