Министерство образования и науки Республики Казахстан

Атбасарский районный отдел образования

Акмолинской области

Открытый урок по алгебре в 11классе

Логарифмические уравнения решаемые с помощью квадратных уравнений

подготовила учитель математики

высшей категории Исабекова Кульжаган Нурхамит

вечерняя сменная средняя общеобразовательная школа

2015год

Тақырып: Логарифмические уравнения решаемые с помощью квадратных

уравнений

Цели:

образовательная: научить применять квадратные уравнения при решении логарифмических уравнений;

развивающая: формировать приемы умственной деятельности: сравнения, аналогии, сопоставления, углублять и систематизировать знания по теме;

воспитательная: учить преодолевать трудности, работать в быстром темпе, воспитывать стремление к совершенствованию знаний

.

Тип урока: комбинированный

Форма урока: классно-урочная

Сабақтың барысы:

1. Организационный момент (приветствие, проверка готовности обучающихся к уроку).

2. Постановка цели.

Мне бы хотелось взять эпиграфом к нашему уроку высказывание древнекитайского философа

Три пути ведут к знанию:
путь размышления – это путь самый благородный,
путь подражания – это путь самый легкий и
путь опыта – это путь самый горький.

Конфуций

Значит, на уроке мы будем размышлять, подражать, т.е. делать по образцу и набираться опыта.
Я хочу вам предложить сыграть в морской бой. Я называю букву строки и номер столбца, а вы называете ответ и ищите соответствующую букву в таблице.

1.Разминка «Морской бой»

1

2

3

4

5

6

7

8

9

А

B

C

D

E

F

G

Класс разбит на три подгруппы и у каждой подгруппы свое задание.

Группа 1

A3, G4, D9, B5, D8, F5, G7, C9, E3, A8 ПЬЕР ЛАПЛАС

8

-3

3

2

0

4

Е

А

П

Р

Л

Ь

C

Группа 2

E6, A4, F5, B9, G8, F1, C4, E1, D5 ДЖОН НЕПЕР

-3

5

3

63

-2

О

Ж

Д

Н

Р

П

Е

Группа 3

A2, B3, G5, D7, C2, E2, F9, B6, E5, G2, D4 УИЛЬЯМ ОТРЕД

1

0

3

-3

7

-1

9

Т

Ь

Д

О

Е

У

Р

И

Я

М

Л

Проверка результатов.

2.Работа по результатам

Джон Непер - шотландский математик. Джону Неперу принадлежит сам термин «логарифм», который он перевел как «искусственное число». После 25-летних вычислений он опубликовал свои таблицы только в 1614 году. Они вышли под названием «Описание чудесных логарифмических таблиц». В 1615 году Непера посетил оксфордский профессор математики Генри Бригс. Непер уже был болен, поэтому не смог усовершенствовать свои таблицы, однако дал Бригсу рекомендации видоизменить определение логарифма, приблизив его к современному. Бригс опубликовал свои таблицы в год смерти Непера (1617). Они уже включали десятичные, а не натуральные, логарифмы, и не только синусов, но и самих чисел (от 1 до 1000, с 14 знаками). Логарифм единицы теперь, как положено, был равен нулю.

Уильям Отред - английский математик. (Слайд 4) Известен как изобретатель логарифмической линейки (1622 год) и один из создателей современной математической символики. Во всём мире логарифмические линейки широко использовались для выполнения инженерных расчётов примерно до начала 1980-х годов, когда они были вытеснены калькуляторами. Отред — автор нескольких стандартных в современной математике обозначений и знаков операций:

• Знак умножения — косой крестик: ×.

• Знак деления — косая черта: /.

• Символ параллельности: .

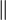• Краткие обозначения функций sin и cos.

• Термин «кубическое уравнение»

Пьер Лаплас - французский математик. Почти четыреста лет прошло с того дня, как в 1614 году были опубликованы первые логарифмические таблицы. Значение логарифмов трудно переоценить. Они нужны инженеру и астроному, штурману и артиллеристу, всем, кому приходится вести громоздкие вычисления. Совершенно прав великий французский математик и астроном Лаплас, который сказал: «Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов»

3. Операционно-познавательный этап.

Задача этапа: содействовать активной познавательной деятельности учащихся, направленной на формирование умения решать логарифмические уравнения методом приведения к квадратному уравнению.

Содержание:

1. Составление и запись алгоритма решения уравнения, записанного на доске.

Алгоритм решения уравнения:

1. находим ОДЗ;

2. делаем замену;

3. решаем квадратное уравнение;

4. подставляем корни квадратного уравнения;

5. решаем простейшие логарифмические уравнения;

6. записываем ответ с учетом ОДЗ.

1. учитель

,

ОДЗ: x>0,

,

,

D=16, , ;

, ;

, ,

, .

Ответ: , 27.

2. Решение на доске уравнения .

Решение. ОДЗ: x>0,

,

,

D=9, , ;

, ;

, ,

, .

Ответ: , 9.

3. Индивидуальное решение уравнения . Проверка решения, обсуждение в парах.

Решение. ОДЗ: x>0,

,

,

D=1, , ;

, ;

, ,

, .

Ответ: 10, 100.

Те ученики, у которых ошибки в решении этого уравнения, решают следующие уравнения (самостоятельная работа по закреплению новых знаний):

а) ;

Решение. ОДЗ: x>0,

,

,

D=1, , ;

, ;

, ,

, .

Ответ: 25, 125.

б) .

Решение. ОДЗ: x>0,

,

,

D=25, , ;

, ;

, ,

, .

Ответ: 0.1; 10000.

4. Индивидуальное решение уравнений (самостоятельная работа по закреплению новых знаний):

а) ;

Решение. ОДЗ: x>0,

,

,

,

,

или ,

.

, ;

, ,

.

Ответ: 1, .

б) .

Решение. ОДЗ: х – любое число,

,

,

,

, ;

, ;

, ,

, ,

, .

Ответ: , .

Проверка решения, обсуждение в парах.

9. Заключительное слово учителя.

У великого геометра древности Фалеса спросили:

- Что есть больше всего?

- Пространство, - ответил Фалес

- Что мудрее всего?

- Время.

- Что приятнее всего?

- Достичь желаемого.

Через несколько месяцев желания многих из вас сбудутся. Я желаю вам удачи в достижении этих желаний, но не забывайте о том, что желания ваши исполнятся не по волшебству. Вам надо ещё немного потрудиться, бросить все свои силы на подготовку к экзаменам.

Спасибо за сотрудничество.

Используемая литература:

1.Алгебра и начала анализа 10-11 класс А.Комагоров

2.Сборник тестов для ЕНТ

3.Интернет ресурс