Урок алгебры в 10-м классе. Тема: «Примеры решения тригонометрических уравнений»

Олей Вера Ивановна

учитель математики

Разделы: Преподавание математики

Цель урока:

1. Закрепить навыки решения простейших тригонометрических уравнений.

2. Сформировать понятие решения тригонометрических уравнений сводящихся к квадратным.

3. Развивать умения сравнивать, выявлять закономерности, обобщать.

4. Воспитывать ответственное отношение к труду.

Оборудование:

1. Карточки для повторения формул решения простейших тригонометрических уравнений.

2. Плакат с алгоритмом решения тригонометрических уравнений (большой на доску и каждому на стол).

Литература: Учебник Мордкович А.Г.“Алгебра и начала анализа, 10-11 класс”.

Ход урока.

I. Повторение

1. sin x = a, cos x = a, tg x = a

При каких значениях а эти уравнения имеют решения?
[sin x и cos x при /а/  1 tg x при любом a]

2. Повторить формулы решения простейших тригонометрических уравнений (на карточках):

sin x = а х = (-1)^к arc sin a+ к, к  z
sin x = 0
sin x = 1
sin x = -1

cos x = a x=± arc cos a + 2 , n  z
cos x = 0
cos x = 1
cos x = -1

tg x = a x = arc tg a + n, n  z

arc sin (-а) = - arc sin а
arc cos (-а) =  - arc cos а
arc tg а (-а) = - arc tg а

II. Проверка домашнего задания.

Игра “Поле чудес”. Правила игры несколько изменены, а название оставлено.

Правила игры.

• Учитель берет понравившееся ему высказывание или слова из песни, стихотворения, пословицу. По количеству букв в этом высказывании подбирается столько же примеров или задач так, чтобы одинаковым буквам соответствовали одинаковые ответы.

• Каждому ученику учитель дает карточку с заданиями и ученик сразу начинает решать.

• На доске записаны буквы, которые встречаются в высказывании, и под ними ответы, которые соответствуют этим буквам.

• Ниже записаны числа по порядку (по количеству букв в высказывании).

• Ученик, выполнявший задание, называет номер своей карточки и букву, под которой записан ответ.

• Учитель под числом (…) ставит букву (…). И так далее. Ученики стараются быстрее решить, чтобы получить следующую карточку.

• За правильно решенные 2-3 задания он может получить оценку. Поэтому желательно карточек иметь более чем число.

Ум хорошо, а два лучше
12 3 45 67 8 9 10 11 12 13 14 15 1 6 17

Уравнение:

Дополнительные уравнения

III. Объяснение нового.

1.

• В предыдущих параграфах были выведены формулы корней простейших тригонометрических уравнений: sin x=a, cos x=a, tg x=a

• К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства из них требуется применение формул преобразований тригонометрических выражений.

• Сегодня на уроке мы рассмотрим уравнение, сводящиеся к квадратным.

2.

• На доске записаны уравнения:

а) 3х-8=х+6 (линейное уравнение)
б) х²+2х-15=0 (квадратное уравнение)
в) х⁴-5х²+4=0 (квадратное уравнение относительно х²).
г) 2 cos²x-cosx-1=0 (квадратное уравнение относительно cosx)

• Какие из них являются квадратными?

• Общий вид квадратного уравнения:

ax²+bx+c=0

, 

Корни квадратного уравнения, приведенного, т.е. х²+рх+q=0 можно находить по теореме Виета:

Х₁+х₂=-р; х₁х₂=q

• х⁴-5х²+4=0 – квадратное уравнение относительно х². Это уравнение назвали биквадратным. Общий вид ах⁴+вх²+с=0, где а± 0.

• Его легко решить методом введения новой переменной, т.е. х²=а и уравнение принимает вид: а²-5а+4=0

3. Последнее уравнение тоже квадратное, относительно cosx. Для его решения введем новую переменную. Пусть y=cosx, тогда уравнение можно записать виде: 2у²-у-1=0. Получили квадратное уравнение.

Д=1+8=9;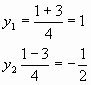 

Следовательно:

а) cosx=1 б) cosx=

х=2p n, n  z , n  z

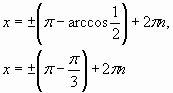
 , n  n

Ответ: 2 n, n  z; , n  z

4. Решим уравнение:

 Надо привести уравнение к одной функции. Для этого заменим cos² x на 1-sin²x. Получим относительно xinx квадратное уравнение:

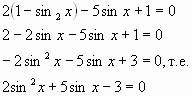
Пусть xinx=у, тогда 2у²+5у-3=0

Получили квадратное уравнение

Д=25+24=49

; 

Следовательно:

а)  б) xinx=-3 – решение не имеет

, к  z

, к  z

Ответ: , к  z

5.

tgx-2ctgx=-1. Функции разные. Используя тождество tgx? ctgx=1, выразим , заменим ctgxчерез tgx.

 пусть tgx=у, то у²+у-2=0 (дальше, как в предыдущем случае).

6. Для закрепления

4 xin²x- cosx-1=0
Заменим xin²x на 1- cos²x. Получим
4(1- cos²x)- cosx-1=0
4-4 cos²x- cosx-1=0
-4 cos²x- cosx+3=0
4 cos²x+ cosx-3=0

пусть cosx=у, то

4у²+у-3=0

Д=1-48=49 ; 

Следовательно,

а) cosx=-1 б) 

х= +2 n, n  z , n  z

Ответ:  +2 n; , n  z

7. №164 (в) - cамостоятельно

2 xin²x- xinx-1=0
пусть xinx=у, то
2у²-у-1=0

Д=1+8=9;  

Следовательно,

а) xinx=1 б) 

, n  z , n  z

,к  z.

Ответ: , n  z

, к  z

№ 165(б)

2 xin²x+3 cosx=0

Заменим xin²x на 1- cos²x получим

2(1- cos²x)+3 cosx=0
2-2 cos²x+3 cosx=0
-2 cos²x+3 cosx+2=0, т.е.
2 cos²x-3 cosx-2=0

пусть cosx=у, то
2у²-3у=0

Д=9+16=25

; 

Следовательно,

а) cosx=2 б) 

решение не имеет , n  z

, n  z

, n  z

Ответ: , n  z

8.

Итог урока

Алгоритм решения тригонометрических уравнений.

1. Привести уравнение к квадратному, относительно тригонометрических функций, применяя тригонометрические тождества.

2. Ввести новую переменную.

3. Записать данное уравнение, используя эту переменную.

4. Найти корни полученного квадратного уравнения.

5. Перейти от новой переменной к первоначальной.

6. Решить простейшие тригонометрические уравнения.

7. Записать ответ.