Конспект урока по Алгебре "Решение квадратных уравнение различными способами" 8 класс

МОУ Большеключищенская средняя общеобразовательная школа имени В.Н. Каштанкина

Выполнила: Ушкова Анна Викторовна

учитель математики второй

квалификационной категории

2013-2014 уч.год

Цель урока:

Обобщение темы: «Квадратное уравнение»; создание условий для осознанного и уверенного владения навыком решения квадратных уравнений, рассмотрение различных способов решения квадратных уравнений.

Образовательные задачи урока:

систематизировать знания, выработать умение выбирать рациональный способ решения квадратных уравнений, расширить и углубить представления учащихся о решении уравнений, организовать поисковую деятельность учащихся при решении квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.

Развивающие задачи урока:

развивать математическое мышление, память, внимание; развивать умение анализировать, сравнивать, обобщать, классифицировать, строить умозаключения, делать выводы; развивать коммуникативные навыки; навыки самостоятельной работы; развивать устную и письменную речь учащихся; привить любовь к предмету, желание познать новое.

Воспитательные задачи урока:

воспитывать культуру умственного труда;

воспитывать культуру коллективной работы;

воспитывать информационную культуру;

воспитывать потребность добиваться успехов в приобретении знаний; воспитание навыков самоконтроля и взаимоконтроля, развитие самостоятельности и творчества.

Формы обучения:

Индивидуальная, фронтальная работа, парная работа, взаимопомощь, групповая (коллективная) деятельность.

Тип урока:

Урок обобщения и систематизации знаний.

Оборудование:

Компьютер, мультимедийная установка, презентация, листы учета знаний, карточки.

Ход урока:

I. Организационный момент.

Цель: формирование мотива, желания работать на уроке.

Здравствуйте, ребята.

Чтобы у нас царила атмосфера доброжелательности, предлагаю начать урок со слов персидско-таджикского поэта Рудаки:

«С тех пор как существует мирозданье

Такого нет, кто б ни нуждался в знанье.

Какой мы ни возьмём язык и век,

Всегда стремится к знанью человек.»

(СЛАЙД 1)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\NoName.bmp$

А законы у нас сегодня будут такие: каждый из вас имеет возможность получить оценку за урок по результатам работы на различных его этапах. Для этого у вас на партах лежат карты результативности (приложение 1), в которые вы будете фиксировать свои успех в баллах. И еще один не обсуждаемый закон: для ответа на поставленный вопрос вы поднимаете руку и ни в коем случае не перебиваете друг друга. Желаю всем удачи.

IΙ. Подготовка учащихся к восприятию темы.

Чтобы определить тему урока, нужно выполнить следующее задание:

Какие слова зашифрованы?

Таиимдкисрнн - дискриминант
Ниваренуе - уравнение
Фэкоцинетиф - коэффициент
Ерокнь – корень

(СЛАЙД 2)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\1.bmp$

С каким понятием связаны понятия «дискриминант», «коэффициент», «корень» ?

Над какой учебной задачей мы с вами будим работать на уроке?

Итак тема нашего урока: «Решение квадратных уравнений различными способами». (СЛАЙД 3)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\2.bmp$

IΙΙ. Постановка цели урока.

Что нужно знать и уметь делать, чтобы решить квадратное уравнение?

Какую цель мы поставим сегодня на уроке?

Цели урока:

1. Обобщение и систематизация основных знаний и умений по теме

2. Формировать умения, решать квадратные уравнения различными способами

3. Формировать умения применять математические знания к решению практических задач;

(СЛАЙД 4)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\3.bmp$

ΙV. Актуализация опорных знаний.

Цель: повторение необходимых теоретических сведений по теме, развитие умений говорить и слушать.

Вот давайте и проверим, насколько хорошо вы усвоили определения и понятия которые мы с вами применяем при решении уравнений. Решите кроссворд. Работаем в паре. (приложение2)

(СЛАЙД 5)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\4.bmp$

Какое ключевое слово получилось?

Уравнения с давних времен волновали умы человечества. По этому поводу у английского поэта средних веков Чосера есть прекрасные строки, предлагаю сделать их эпиграфом нашего урока:

Посредством уравнений, теорем
Я уйму всяких разрешил проблем.

(СЛАЙД 6)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\5.bmp$

Квадратные уравнения тоже не исключение. Они очень важны и для математики, и для других наук.

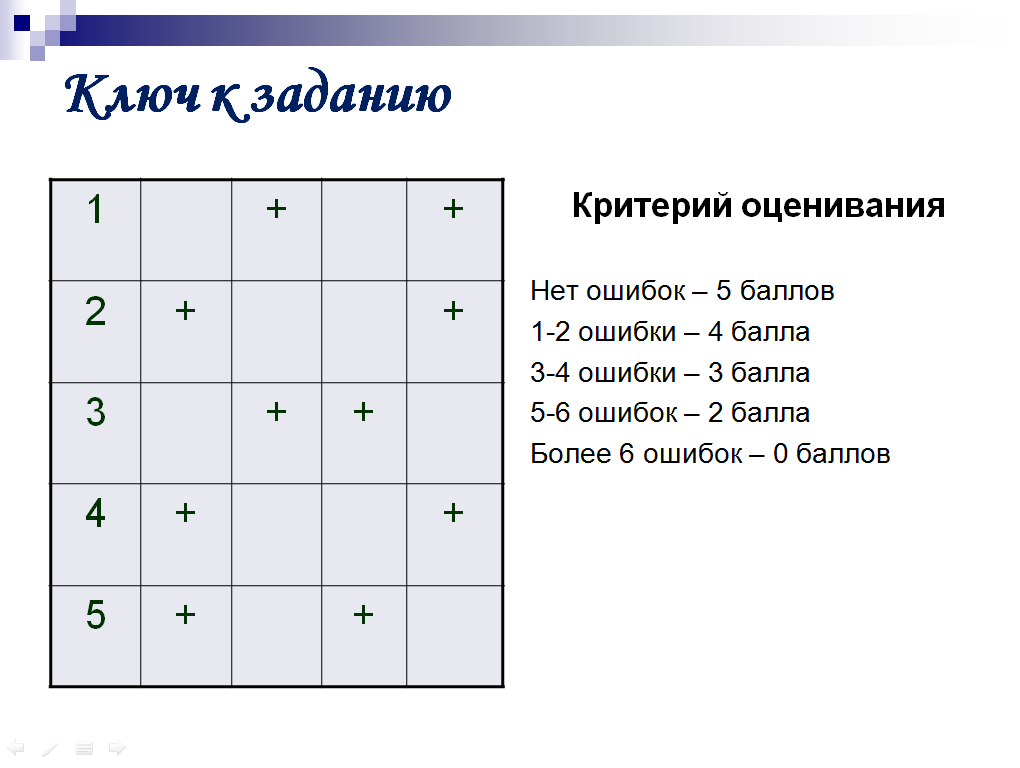
«ЧУТЬ – ЧУТЬ ПОДУМАЙ» - учащиеся заполняют таблицу (приложение 3) индивидуально, а затем взаимопроверка.

(СЛАЙД 7-8)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\7.bmp$

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\8.bmp$

V. Работа в группах.

Цель: повторение способов решения полных квадратных уравнений.

Сегодня мы с вами решим одно квадратное уравнение х² - 6х-7=0 и постараемся вспомнить все способы, которые мы уже знаем.

(СЛАЙД 9)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\9.bmp$

Открыли тетради. Записали число: «22.01.2014».

Тема урока: «Решение квадратных уравнений различными способами».

Запишите уравнение: х² - 6х-7=0

Работаем в группах (по рядам).

На листочках написан способ, которым вы должны решить квадратное уравнение и затем защитить своё решение:

Способ № 1.

«По общей формуле, через дискриминант».

Способ № 2.

«С помощью формулы корней квадратного уравнения с четным вторым коэффициентом».

Способ № 3:

«Метод выделения полного квадрата».

Закончили решение. Разбираем ваши способы решения, остальные группы пишут в тетрадь.

Сейчас, представитель каждой группы расскажет о своем методе решения данного уравнения. Пожалуйста, 1 группа.

Интересный факт (сообщение ученика)

Дискриминант дает возможность определить число корней квадратные уравнения. В математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Вспомните слово «дискриминация».

Что оно означает? …

Правильно. Оно означает унижение одних и возвышение других, то есть различное отношение к различным людям. Оба слова (и дискриминант, и дискриминация) происходят от латинского - «различающий». Дискриминант различает квадратные уравнения по числу корней.

VI. Физминутка.

Цель: смена деятельности, отдохнуть.

Правила выполнения зарядки:

перед началом упражнений прикройте глаза ладошками, почувствуйте тепло рук. Откройте глаза, расслабьтесь
сядьте прямо, держите голову ровно
за движущимися предметами на слайде следите только глазами
если предмет вращается, делайте глазами круговые движения

(СЛАЙД 10-11)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\10.bmp$

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\11.bmp$

VII. Изучение нового материала.

Цель: познакомиться с теоремой Виета

Открою вам большой секрет – есть еще очень много методов решения квадратных уравнений и сегодня мы узнаем один из них.

ЛАБОРАТОРНАЯ ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

Разбиваем класс на четыре группы, каждой из которых дать решить приведённое уравнение (приложение 4). После его решения один представитель от каждой группы выходит к доске и заполняет соответствующую строку в таблице.

(СЛАЙД 12)

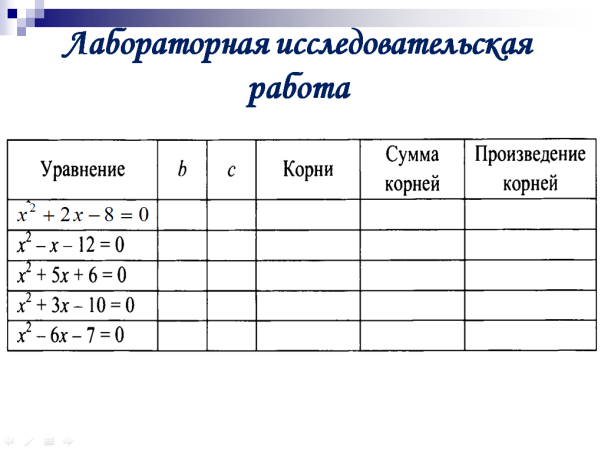
$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\12.bmp$

После этого учитель предлагает учащимся сравнить сумму и произведение полученных корней с коэффициентами в и с, выдвинуть гипотезу.

Учитель подтверждает сделанное предположение, сообщая, что данное утверждение называется теоремой Виета, обращая внимание учащихся, что эта теорема справедлива для приведённых квадратных уравнений.

(СЛАЙД 13)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\13.bmp$

VIII. Исторические сведения
Цель: формирование учебно-познавательной мотивации школьников на уроке, воспитание интереса к предмету.

Ученик представляет краткий исторический материал о жизни и деятельности Франсуа Виета.

(СЛАЙД 14)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\14.bmp$

Обращаем внимание учащихся, что по теореме Виета мы можем только убедиться в правильности нахождения корней с помощью дискриминанта. А если мы подберём такие числа, которые в сумме будут равны второму коэффициенту с противоположным знаком, а в произведении – свободному члену, то не будут ли они являться корнями уравнения? Подчёркиваем, что мы хотим воспользоваться утверждением, обратным теореме Виета.

(СЛАЙД 15-16)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\15.bmp$

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\16.bmp$

IХ. Решение уравнений

Цель: формирование умений и навыков решения квадратных уравнений с помощью теоремы обратной теоремы Виета.

Вернёмся к нашему уравнению х² - 6х-7=0 и решим его четвёртым способом, с помощью обратной теоремы Виета. Один ученик работает у доски.

(СЛАЙД 17)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\17.bmp$

Х. Проверочная работа.

Цель: первичная проверка знаний учащихся.

(СЛАЙД 18-19)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\18.bmp$

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\19.bmp$

ХΙ. Подведение итогов урока.

- Сформулируйте теорему Виета.

- Что необходимо проверить, прежде чем находить сумму и произведение корней приведённого уравнения?

- Как можно применить теорему Виета для неприведённого квадратного уравнения?

- В чём состоит теорема, обратная теореме Виета? Когда она применяется?

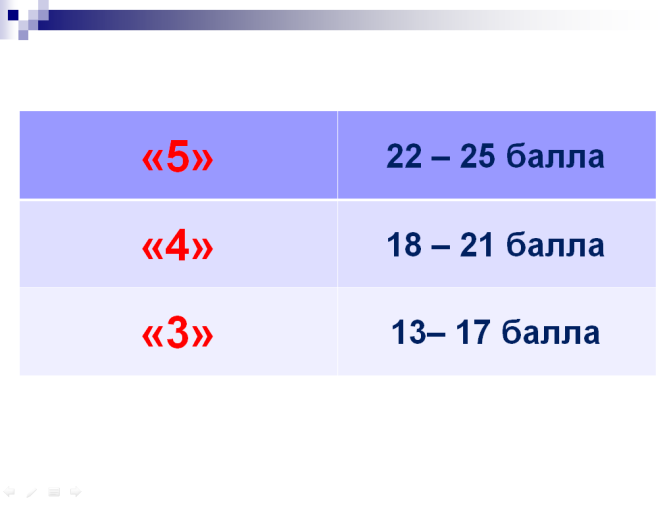
Сегодня на уроке мы с Вами разобрали 4 способа решения одного квадратного уравнения. Возьмите лист учета знаний и подсчитайте свой результат.

(СЛАЙД 20)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\20.bmp$

Мы убедились, что пути решения даже одной и той же задачи могут быть очень разнообразными.

И закончить сегодняшний урок хотелось бы словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»

ХΙΙ. Домашнее задание:

П. 24 стр.132 – вопросы;

№ 584;

№ 599 / новые способы решения квадратных уравнений /

(СЛАЙД 21)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\21.bmp$

Квадратные уравнения прошли,

Итог сегодня подвели.

Смелей шагайте вы вперед,

Много нового вас ждет.

Спасибо вам за знания,

За ваши все старания!

(СЛАЙД 22)

$C:\Users\Дом\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\22.bmp$

Литература:

Учебник: Алгебра: учеб. для 8 кл. общеобразоват. учреждений/ [Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова]; под ред. С.А. Теляковского. – М.: Просвещение, 2008
Алгебра. 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой/ авт.-сост. Т.Ю. Дюмина, А.А. Махонина, - Волгоград: Учитель, 2011
http://nsportal.ru – социальная сеть работников образования.

http://nsportal.ru/shkola/algebra/library/library/urok-algebry-sposoby-resheniya-kvadratnykh-uravnenii-8-klass

http://rpp.nashaucheba.ru/docs/index-129121.html

ПРИЛОЖЕНИЕ 1.

8 «А» класс

Карта результативности.

Ф.И.

Зашифрованные слова

(анаграммы)

Кроссворд

Чуть-чуть подумай

Решение уравнений

Лабораторная исследовательская работа

Проверочная сам. работа

ИТОГО

Количество

баллов

ПРИЛОЖЕНИЕ 2.

Кроссворд

ПРИЛОЖЕНИЕ 3.

Чуть – чуть подумай!

Уравнение

Полное

Неполное

Приведенное

Неприведенное

6х²+9=0

-х²+2х+4=0

х²-3х=0

3х+6х²+7=0

х+ х²+3=0

ПРИЛОЖЕНИЕ 4.

Лабораторная исследовательская работа (1 группа)

Решите уравнение:
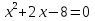
Заполните таблицу

Уравнение

Корни

Сумма корней

Произведение корней

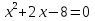
Сравните сумму и произведение полученных корней с коэффициентами b и с и сформулируйте гипотезу ___________________________________________________

________________________________________________________________________________________________________________________________________________________

Лабораторная исследовательская работа (2 группа)

Решите уравнение:
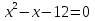
Заполните таблицу

Уравнение

Корни

Сумма корней

Произведение корней

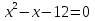
Сравните сумму и произведение полученных корней с коэффициентами b и с и сформулируйте гипотезу____________________________________________________
________________________________________________________________________________________________________________________________________________________

Лабораторная исследовательская работа (3 группа)

Решите уравнение:
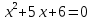
Заполните таблицу

Уравнение

Корни

Сумма корней

Произведение корней

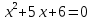
Сравните сумму и произведение полученных корней с коэффициентами b и с и сформулируйте гипотезу____________________________________________________

________________________________________________________________________________________________________________________________________________________

Лабораторная исследовательская работа (4 группа)

Решите уравнение:
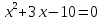
Заполните таблицу

Уравнение

Корни

Сумма корней

Произведение корней

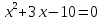
Сравните сумму и произведение полученных корней с коэффициентами b и с и сформулируйте гипотезу____________________________________________________

________________________________________________________________________________________________________________________________________________________

Листать вверх Листать вниз

Получить код

Скачать материал (2.37 Мб)

Нравится материал? Поддержи автора!

Ещё документы из категории алгебра:

Конспект урока по Алгебре "Решение простейших тригонометрических уравнений"

Конспект урока по Алгебре "Линейное уравнение с одной переменной" 7 класс

Конспект урока по Алгебре "Сложение и вычитание смешанных чисел" 5 класс

Конспект урока по Алгебре "Обратные тригонометрические функции" 10 класс

Конспект урока по Алгебре "Производная показательной и логарифмической функции"

Конспект урока по Алгебре "Прямая и обратная пропорциональные зависимости" 6 класс

Конспект урока по Алгебре "Решение уравнений" 5 класс