Конспект урока по Алгебре "Решение логарифмических уравнений" 10 класс
КАЗЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ОМСКОЙ ОБЛАСТИ
«ВЕЧЕРНЯЯ (СМЕННАЯ) ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №2»
Разработка групповой консультации по алгебре и началам математического анализа в 10 классе.
Учитель математики: Андриевская Нина Фёдоровна
высшая квалификационная категория
Тема групповой консультации:
«Решение логарифмических уравнений» (2часа)
Цели групповой консультации:
Образовательная цель групповой консультации: Научиться решать логарифмические уравнения в соответствии с их видами (типами), используя рациональные методы и приёмы их решения.
Воспитательная цель групповой консультации : Развитие навыков и умений коллективных методов работы, воспитание уважения и терпимости друг к другу, умения слушать и общаться друг с другом.
Развивающая цель групповой консультации. Развитие навыков логического мышления, ознакомление с историей возникновения учения о логарифмах.
Групповая консультация реализуется с использованием адаптивной системы обучения.
Краткая характеристика контингента обучающихся.
Состав учащихся заочной группы представляет собой обучающихся-осуждённых переводного контингента и учащихся нового набора. Ученики переводного контингента, проучившиеся в школе от 1 до 5 лет, значительно отличаются от новичков хорошей дисциплиной, положительной мотивацией к учебному труду, общей культурой, необходимыми опорными знаниями по предметам, уважительным отношением к школе, к учителям. На начало учебного года заочные группы формируются как из переводного контингента, так и из учащихся нового набора. Многолетняя практика школы показала эффективность такого образования классных коллективов. Учащиеся переводного контингента оказывают положительное влияние на новичков, происходит воспитание в коллективе через коллектив. Для работы учащихся в группах обязательно учитывается психологическая совместимость обучающихся. Многие новички часто имеют значительный перерыв в учёбе, большие пробелы в знаниях, часто негативный опыт детской школы, низкую мотивацию учебного труда, неоднократные судимости. Всё это требует от учителя определённых усилий для вовлечения осуждённых в активную познавательную деятельность. Неразвитые психофизические процессы обучающихся, такие, как память, внимание, мышление требуют от учителя внедрения отлаженной системы повторения, закрепления опорных знаний и выстраивания личностной траектории развития каждого учащегося по предмету. Кроме того, учебные планы, учебные программы, учебники и методические пособия не учитывают специфику обучения взрослых, тем более специфику обучения взрослых- осуждённых. Решение проблем адаптации учебно-методических материалов детской школы к условиям обучения взрослых возложили на себя педагоги открытых вечерних школ и педагоги школ пенитенциарной системы.
Оборудование: учебники «Математика» Бутузов В.Ф., Калягин Ю.М., Луканкин Г.Л. и др., записи вопросов на доске, опорные таблицы, дидактический материал обучающего, развивающего и контролирующего характера трёх-четырёх уровней сложности с необходимыми формулами и опорными сигналами, ноутбук, мультимедиапроектор, экран.
1этап. Объяснение нового материала, обучение приёмам самостоятельной работы.( 10-12 минут).
Определяются учебные цели групповой консультации. Повторяются такие понятия, как уравнение, степень числа, логарифм числа, основание логарифма, понятие основного логарифмического тождества, формулы логарифмов, даётся информация из истории развития логарифмов. Даются пояснения по использованию опорной таблицы (Приложение). Используется мультимедиапроектор, экран. Основной упор занятия учитель делает именно на презентацию и разработанные материалы приложения.
Учитель даёт учащимся консультации по работе с пакетом дидактического материала обучающего, развивающего и контролирующего характера трёх - четырёх уровней сложности с необходимыми формулами и опорными сигналами. Дидактический материал содержит 5 основных видов логарифмических уравнений: логарифмические уравнения, решаемые по определению логарифма; логарифмические уравнения, решаемые потенцированием; логарифмические уравнения второй степени и выше относительно логарифма; уравнения, содержащие неизвестное в основании и в показателе степени; логарифмические уравнения, решаемые с помощью дополнительных сведений из теории логарифмов. Учащиеся рассматривают решённые уравнения, запоминают виды уравнений, методы и приёмы их решения.
У каждого ученика на столе имеется учебник, пакет с дидактическими материалами обучающего, развивающего и контролирующего характера (Приложение). По мере работы с дидактическим материалом учитель выявляет затруднения в усвоении учащимися учебного материала, отрабатывает понятийный аппарат, направляет работу учащихся на оптимальный выбор приёмов и методов решения основных видов логарифмических уравнений.
Учитель обращает внимание учащихся на то, что правильность решения уравнения можно проверить либо проверкой найденных корней, либо нахождением области определения уравнения. (В дидактических материалах выделено зелёным цветом).
При применении некоторых формул логарифмов используются ряд сигнальных обозначений.
Для ряда учащихся, имеющих значительные пробелы в знаниях, имеются необходимые для решения логарифмических уравнений опорные правила и формулы. Например, свойства степени, свойства корней, формулы решения квадратных уравнений, правила вынесения общего множителя за скобки.
Учитель обращает внимание обучающихся на единый орфографический режим при выполнении заданий, требует от учащихся чёткости и аккуратности при оформлении.
Пакет дидактических материалов обучающего, развивающего и контролирующего характера (Приложение) прилагается.
II этап. Работа в группах, взаимоконтроль учащихся.
Учащиеся разбиваются на группы 2-4 человека в каждой. Каждый член группы получает индивидуализированное задание по решению уравнений по образцу. Школьники с более высокими учебными возможностями становятся консультантами для более слабых учащихся. Разнообразятся виды деятельности обучающихся. Ученики обмениваются тетрадями друг с другом. Работа по образцу (на 1 этапе) позволяет отработать навыки решения уравнений по видам, закрепляет навыки оформления решённых уравнений, учит распознавать виды уравнений, позволяет обучающимся рационально распределить свои силы, утвердиться, проявить инициативу, находчивость, обрести чувство сопричастности к учебному труду, победить страх. Учитель включается в работу групп в разных качествах: участника, консультанта, помощника. Он отслеживает степень усвоения учебного материала, предлагает необходимые источники информации, оказывает помощь в ликвидации пробелов в знаниях и в овладении необходимых знаний, умений и навыков.
III этап. Обособленная самостоятельная работа, самоконтроль.
На этом этапе наиболее успешным ученикам предлагаются задачи для самостоятельного решения. Для определения вида уравнения от учащихся требуется хорошее знание свойств и формул логарифмов, других опорных знаний и выполнения ряда первоначальных преобразований.
Учащиеся со средними учебными способностями для самостоятельного выполнения получают задания, в которых вид уравнения установлен по одному из образцов и не требует предварительных преобразований для установления его вида.
Учащиеся с низкими учебными способностями продолжают отрабатывать навыки решения уравнений разных видов 1-2 уровней по образцу, всякий раз добиваясь всё большего понимания и осмысления.
Данное учебное занятие рассчитано на 2 часа. В течение первого часа работа идёт в основном по I и II этапу. Ряд учащихся переходят к выполнению III этапа. Им предлагаются уравнения 2, 3 и 4 уровней.
В 10 классе школы пенитенциарной системы тема «Логарифмические уравнения» изучается впервые. Начальное изучение этой темы целесообразно по адаптивной системе обучения, т.к. учитель, согласно целевым установкам, раскрывает основные определения, понятия, приёмы и методы решения. В 12 классе при повторении этой же темы целесообразно использование модульной технологии, т.к. учащиеся уже имеют представление о логарифмах и в дальнейшем могут самостоятельно осваивать (повторять) данный модуль.
В конце урока подводятся итоги занятия, выставляются и комментируются оценки, объявляются требования и критерии к выполнению зачёта по изученной теме.
Презентация к занятию
ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
( П Р И Л О Ж Е Н И Е)
Дидактический материал обучающегося, развивающего и контролирующего характера для учащихся 10 классов и для повторения темы в курсе 12 класса вечерней школы.
Определение логарифма
Логарифмом положительного числа b по основанию а, где a> 0, а ≠ 1, называется показатель степени, в которую надо возвести основание а, чтобы получить число b.
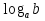 = c; a= 10; lgb ; a = e;
= c; a= 10; lgb ; a = e; 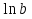
десятичный логарифм натуральный логарифм
Свойства логарифмов. Формулы. Тождества.
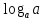 = 1
= 1 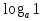 = 0
= 0 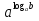 = b
= b
логарифмическая единица; логарифмический нуль; основное логарифмическое
тождество
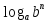 = n ·
= n · 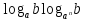 =
= 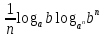 =
= 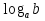
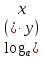 =
= 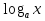 +
+ 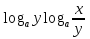 =
= 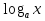 -
- 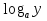
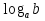 =
= 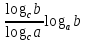 =
= 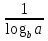
формулы модуля перехода к другому основанию
Логарифмическая функция и ее свойства
у = 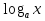 (a> 0, а ≠ 1) (обратная для функции у =
(a> 0, а ≠ 1) (обратная для функции у = 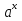 )
)
a> 1; у =
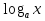 2) 0 <a< 1 ; у =
2) 0 <a< 1 ; у = 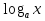
Свойства
Область определения х >0;
Множество значений у=R;
При х = 1 у = 0;
При a> 1 , если 0 <х< 1, то у < 0; если х> 1, то у > 0;
При 0 <a< 1, если 0 <х< 1, то у > 0; если х> 1, то у < 0.
Виды логарифмических уравнений
Уравнения, решаемые с помощью определения логарифма.
I уровень
Пример: 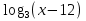 = 2.
= 2.
х – 12 = 32;
х = 9 + 12 ;
х = 21;
Проверка: или область
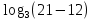 = 2; определения
= 2; определения
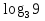 = 2; х – 12 > 0;
= 2; х – 12 > 0;
9 = 32; х > 12;
9 = 9; 21 > 12.
Ответ. 21.
Решить самостоятельно (по образцу)
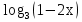 = 1;
= 1;
2) 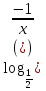 = 4.
= 4.
Основные формулы и понятия:
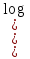 = c) ↔
= c) ↔ 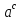 = b
= b
Область определения логарифма.
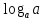 = 1;
= 1; 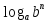 = n
= n 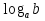
II уровень Проверка: или найти область
Пример: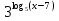 =
= 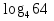 .
. 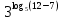 = 3; определения
= 3; определения
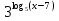 =
= 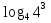 ;
; 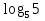 = 1; х – 7> 0;
= 1; х – 7> 0;
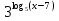 =
= 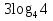 ; 1 = 1. х >7;
; 1 = 1. х >7;
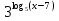 =
= 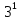 ;
;
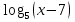 = 1;
= 1;
х – 7 = 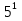 ;
;
х = 5 + 7;
х = 12. Ответ. 12 . 12 > 7 (верно)
III уровень
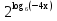 =
= 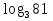 ;
;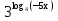 =
= 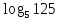 .
.
Пример: 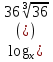 = 2
= 2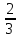 .
.
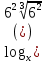 =
= 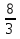 ;
;
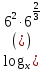 =
= 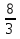 ;
;
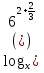 =
= 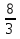 ;
;
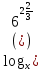 =
= 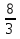 ;
;
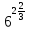 =
= 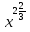 ; х = 6.
; х = 6.
Рациональнее найти область определения и не делать проверку корня.
х >0; 6 > 0 (верно).
Ответ. 6.
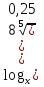 =
= 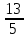 ;
;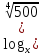 ) – 3 = -
) – 3 = - 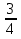 .
.
IV уровень
Пример: 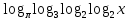 = 0
= 0
Ноль в правой части представить, как
логарифм единицы. Затем выражение, стоящее под знаком крайнего логарифма, приравниваем к единице и т.д.
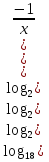 ) = 0
) = 0
Уравнения первой степени относительно логарифма, решаемые потенцированием.
I уровень
Пример: lg(х + 2) – lg 5 = lg( х - 6).
lg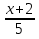 = lg( х - 6);
= lg( х - 6);
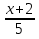 = х – 6;
= х – 6;
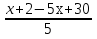 = 0;
= 0;
- 4х + 32 = 0; ׃(- 4)
х – 8 = 0; х = 8.
Проверка: lg( 8 + 2) – lg 5 = lg( 8 - 6);
lg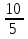 = lg 2;
= lg 2;
lg 2 = lg 2;
2 = 2. Ответ. 8.
Потенцирование – это переход от равенства, содержащего логарифмы, к равенству, не содержащему их.
Решить самостоятельно или по образцу.
lg х – lg 11 = lg 19 – lg(30 – х);
2lg х + lg(6 – х2) = 0;
Основные формулы:
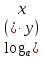 =
= 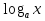 +
+ 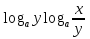 =
= 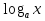 -
- 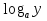
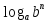 = n ·
= n · 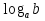
II уровень
Пример: lg(7х – 9)2 + lg(3х – 4)2 = 2.
2lg(7х – 9) + 2lg(3х – 4) = 2;
lg(7х – 9) + lg(3х – 4) = 1;
lg((7х – 9)(3х – 4)) = 1;
21х2 – 28х – 27х + 36 = 101;
21х2 – 55х + 26 = 0;
х1,2 = 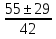 ; х1 = 2; х2 =
; х1 = 2; х2 = 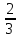 ;
;
Область определения
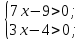 х >
х >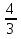 . Ответ. 2.
. Ответ. 2.
lg(х – 1) +
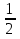 lg(х + 7)2 = lg1.
lg(х + 7)2 = lg1.
III уровень
Пример:
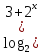 ) +
) + 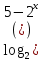 = 4
= 4
В левой: части сумма логарифмов при одном основании равна логарифму произведения.
В правой части: число 4 представить в виде логарифма с основанием 2. Затем приравниваются числа логарифмов (потенцирование).
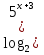 – 1) = 2 +
– 1) = 2 + 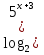 + 1)
+ 1)
IV уровень
Пример:
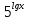 -
- 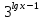 =
= 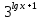 -
- 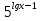
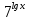 -
- 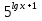 = 3 ·
= 3 · 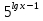 – 13 ·
– 13 · 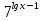
Уравнения второй степени и выше относительно логарифма
-
I уровень
Пример:
lg2 х3 - 10lg х + 1 = 0.
9lg2 х - 10lg х + 1 = 0; lg х = у
9у2 – 10у + 1 = 0;
у1,2 =
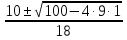 =
= 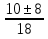 ;
;у1 =
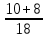 =
= 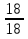 = 1; у2 =
= 1; у2 = 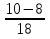 =
= 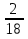 =
= 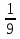 ;
;Область определения х >0
lg х = 1 или lg х =
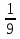 ;
;х = 101; х =
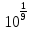 ;
;х = 10; Ответ. 10;
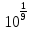 .
.
lg2х – lg х3 + 2 = 0;
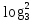 х - 3
х - 3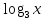 + 2 = 0.
+ 2 = 0.
Основные формулы:
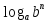 = n ·
= n · 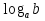 , b>0
, b>0
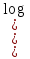 = c) ↔
= c) ↔ 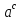 = b
= b
ах2 + bх + с = 0
х1,2 =
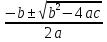
II уровень
Пример:
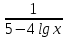 +
+ 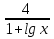 = 3; lg х = у
= 3; lg х = у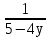 +
+ 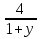 = 3;
= 3;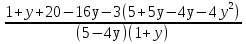 = 0;
= 0;5 - 4у ≠ 0 и 1 + у ≠ 0;
у ≠
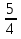 и у ≠ -1;
и у ≠ -1;1+у+20-16у-15-15у+12у+12у2 = 0;
12у2 – 18у + 6 = 0; |:6
2у2 -3у + 1= 0;
у1,2 =
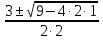 =
= 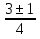 ;
;у1 =
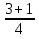 = 1; у2 =
= 1; у2 = 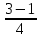 =
= 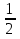 ;
;lg х = 1; lg х =
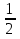 ;
;х = 10; х =
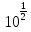 .
.Проверка корней (или нахождение области определения уравнения)
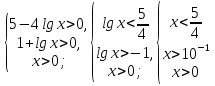
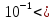 х <
х <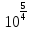
Ответ. 10;
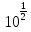 .
.
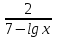 +
+ 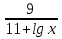 =
= 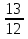 ;
;
Условие равенства дроби нулю:
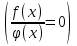 ↔
↔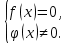
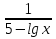 +
+ 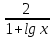 = 1
= 1
IV. Уравнения, содержащие неизвестное в основании и в показателе степени.
-
I уровень
Пример:
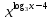 =
= 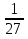 .
.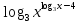 =
= 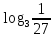 ;
;(
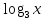 – 4)
– 4) 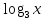 =
= 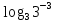 ;
;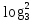 х - 4
х - 4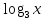 = - 3
= - 3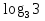 ;
; 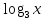 = у
= уу2 – 4у + 3 = 0;
у1 = 1; у2 = 3;
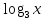 = 1 или
= 1 или 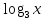 = 3
= 3х =
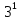 ; х =
; х = 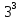 ;
;х = 3. х = 27.
Область определения х >4.
Ответ. 27.
1)
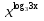 = 9;
= 9;2)
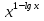 = 0,01.
= 0,01.
Основные формулы:
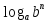 = n
= n 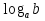 , b>0
, b>0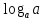 = 1
= 1
у2+ рх + q = 0 по т.Виета
у1 + у2 = - р,
у1 у2 = q.
II уровень
Пример:
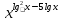 = 0,0001.
= 0,0001.lg (
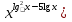 = lg 0,0001;
= lg 0,0001;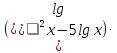 lg х = lg
lg х = lg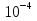 ;
;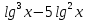 + 4 = 0; lg х = у
+ 4 = 0; lg х = уу3 – 5у2 + 4 = 0;
у0 = 1; у2 – 4у – 4 = 0;
у1 = 1; у2 = 2 + 2
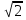 ; у3 = 2 - 2
; у3 = 2 - 2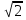 ;
;lg х=1; lg х=2+2
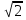 ; lg х = 2-2
; lg х = 2-2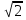 ;
;х =10; х =
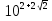 ; х =
; х = 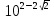
Область определения х > 0
Ответ. 10;
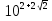 ;
; 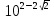 .
.III уровень
Пример:
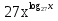 =
= 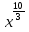 .
.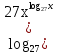 ) =
) = 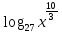 ;
;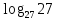 +
+ 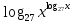 =
= 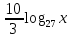 ;
;1 +
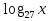 ∙
∙ 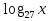 -
- 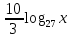 = 0; | ∙3
= 0; | ∙33 + 3
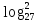 х - 10
х - 10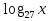 = 0;
= 0; 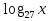 = у
= у3у2 – 10у + 3 = 0;……. продолжить
1)
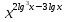 = 0,1;
= 0,1;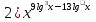 = 0,0001;
= 0,0001;3)
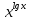 = 100х.
= 100х.
1)
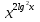 = 10 х3
= 10 х3
V.Логарифмические уравнения, решаемые с помощью дополнительных сведений из теории логарифмов.
-
I уровень
Пример:
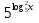 +
+ 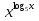 = 10.
= 10.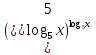 +
+ 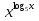 = 10;
= 10;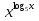 +
+ 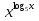 = 10;
= 10;2
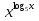 = 10; | :2
= 10; | :2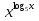 = 5; Обл. определения х >0
= 5; Обл. определения х >0 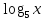 =
= 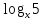 ;
;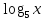 =
= 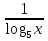 ;
; 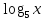 = у
= уу -
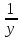 = 0;
= 0; 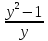 = 0; у ≠ 0;
= 0; у ≠ 0;у2 – 1 = 0; у = ± 1;
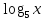 = 1;
= 1; 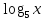 = - 1;
= - 1;
х =
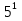 . х =
. х = 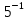 .
.Ответ. 5;
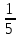 .
.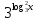 +
+ 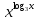 = 6;
= 6;
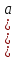 )n=
)n= 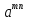
2)
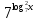 +
+ 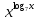 = 14.
= 14.Основные формулы:
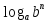 = n ·
= n · 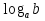 , b>0
, b>0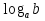 =
= 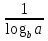
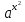 =
= 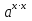 =
= 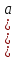 )х
)х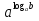 = b
= b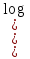 = c) ↔
= c) ↔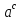 = b
= b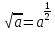
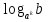 =
= 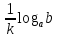
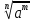 =
= 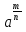
II уровень
Пример:
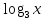 +
+ 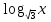 +
+ 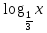 = 6.
= 6.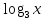 +
+ 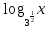 +
+ 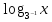 = 6;
= 6;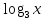 +2
+2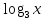 -
- 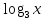 = 6;
= 6;2
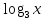 = 6; | :2
= 6; | :2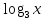 = 3;
= 3; Область определения х >0.
х =
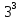 ; Ответ. 27.
; Ответ. 27.
1)
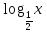 +
+ 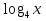 +
+ 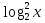 =
= 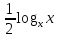 ;
;
2)
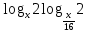 =
= 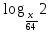 .
.III уровень.
Пример:
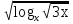 ∙
∙ 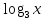 = - 1.
= - 1.Возвести в квадрат обе части уравнения
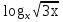 ∙
∙ 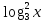 = 1;
= 1;(
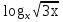 +
+ 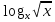 )
) 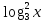 = 1;
= 1;(
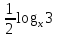 +
+ 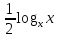 )
) 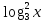 = 1;
= 1;(
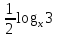 +
+ 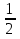 ) ∙
) ∙ 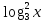 = 1; | ∙2
= 1; | ∙2 (
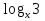 + 1) ∙
+ 1) ∙ 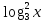 = 2;
= 2;(
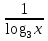 + 1) ∙
+ 1) ∙ 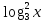 = 2; (подстановка)
= 2; (подстановка)------------- продолжить
1)
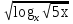 ∙
∙ 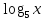 = - 1.
= - 1.
Разработка Андриевской Нины Федоровны, учителя математики КОУ «Вечерняя (сменная) общеобразовательная школа №2», г Омск.

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ