Разработка темы

«Решение тригонометрических уравнений»

в итоговом повторении в 11 классе,

при подготовке к экзаменам.

Цель уроков:

• Повторить и систематизировать раннее изученный материал по решению простейших тригонометрических уравнений.

• Повторить методы решения уравнений.

• Решить сложные уравнения , встречающиеся на ЕГЭ.

• Проверить усвоение материала.

1 урок: «Повторение теоретического материала и решение простейших уравнений» (используя компьютерную презентацию).

2-3 уроки: «Семинар по решению одного уравнения несколькими способами».

4-5 уроки: Решение более сложных уравнений, предложенными способами.

6 урок: Контрольное тестирование по теме, с использованием компьютерной программы.

Урок №1: «Повторение теоретического материала и решение простейших уравнений»

Цель:

1. Повторить и систематизировать раннее изученный материал по решению простейших тригонометрических уравнений.

2. Решение уравнений, с выбором ответов.

3. Воспитывать умение применять полученные знания.

Ход урока:

1. Решение уравнений вида .

2. Решение уравнений вида

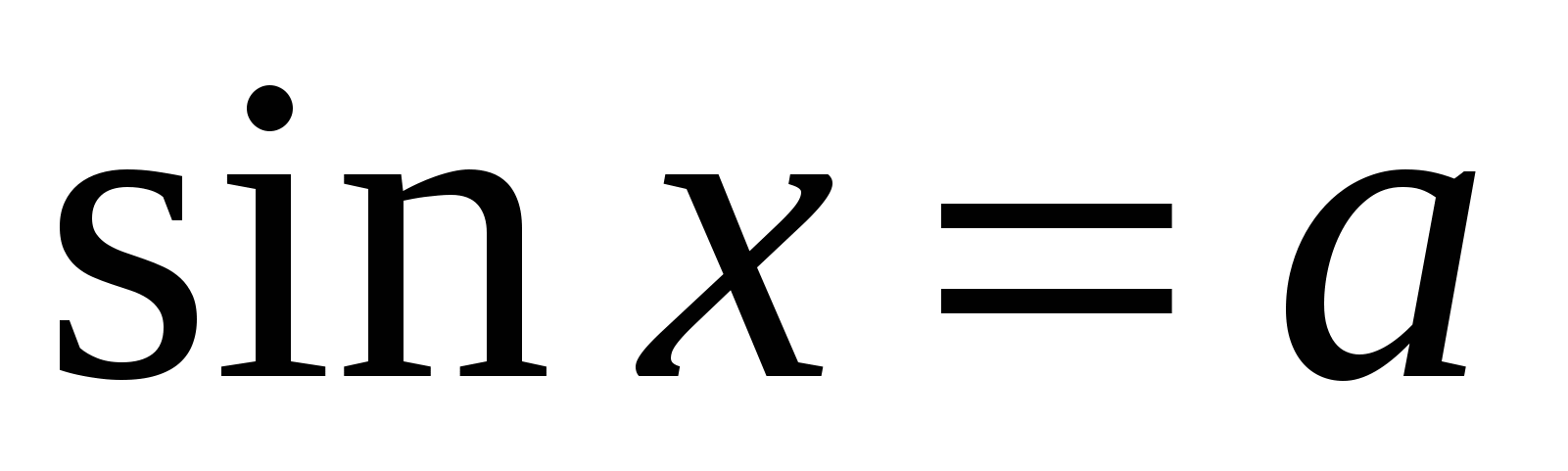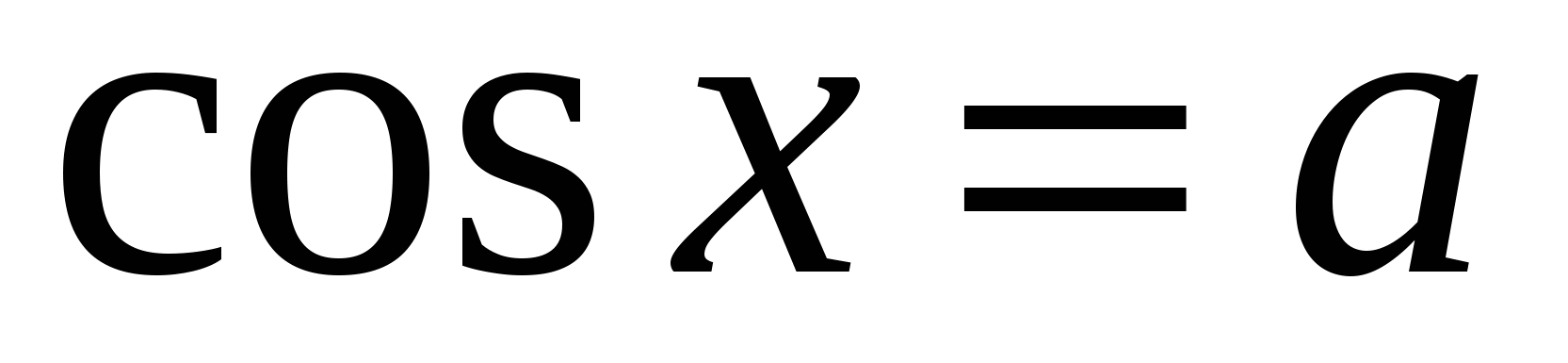
3. Решение уравнений вида 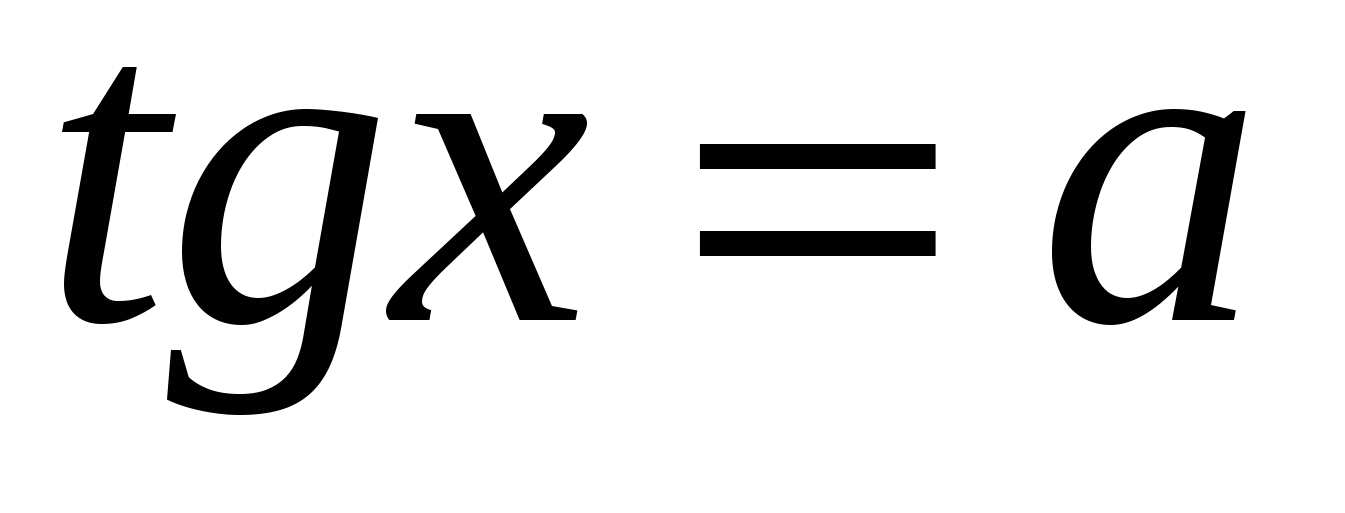и

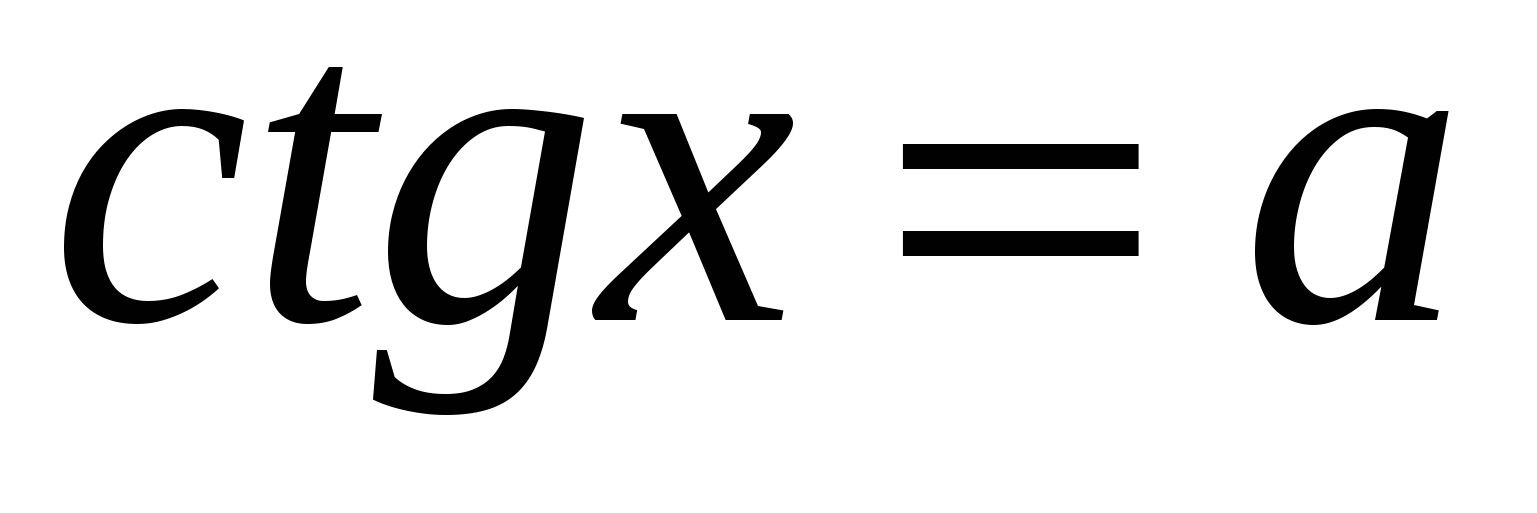
4. Итог урока.

Решение сложных уравнений сводится к решению простейших уравнений:

.

и

Вспомним, как они решаются.

1. Решение простейших тригонометрических уравнений вида:

.

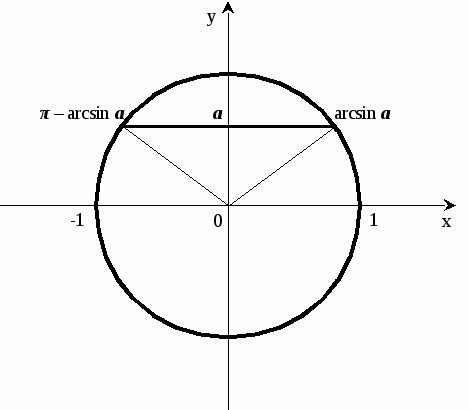
где

Частные случаи:

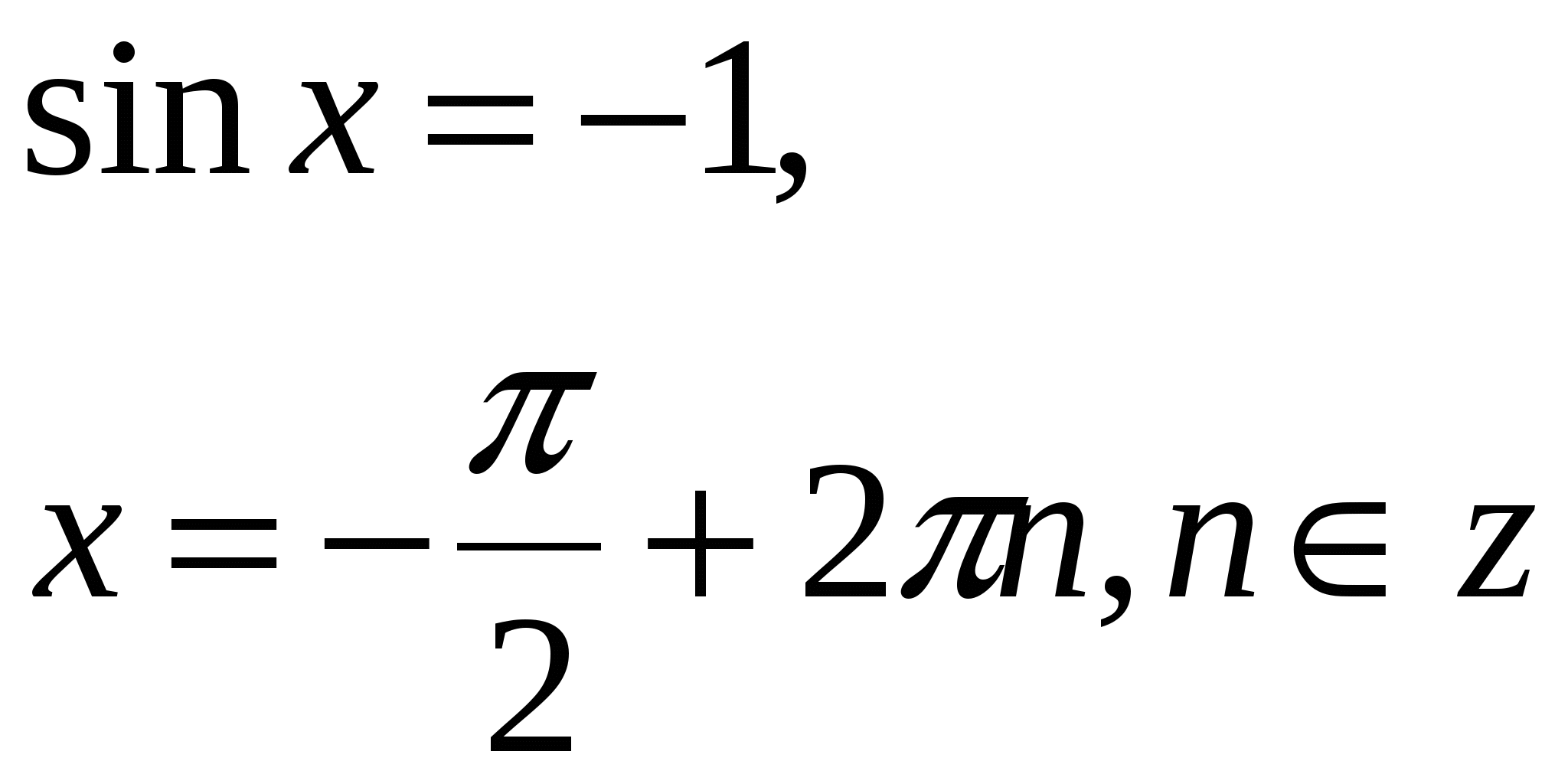
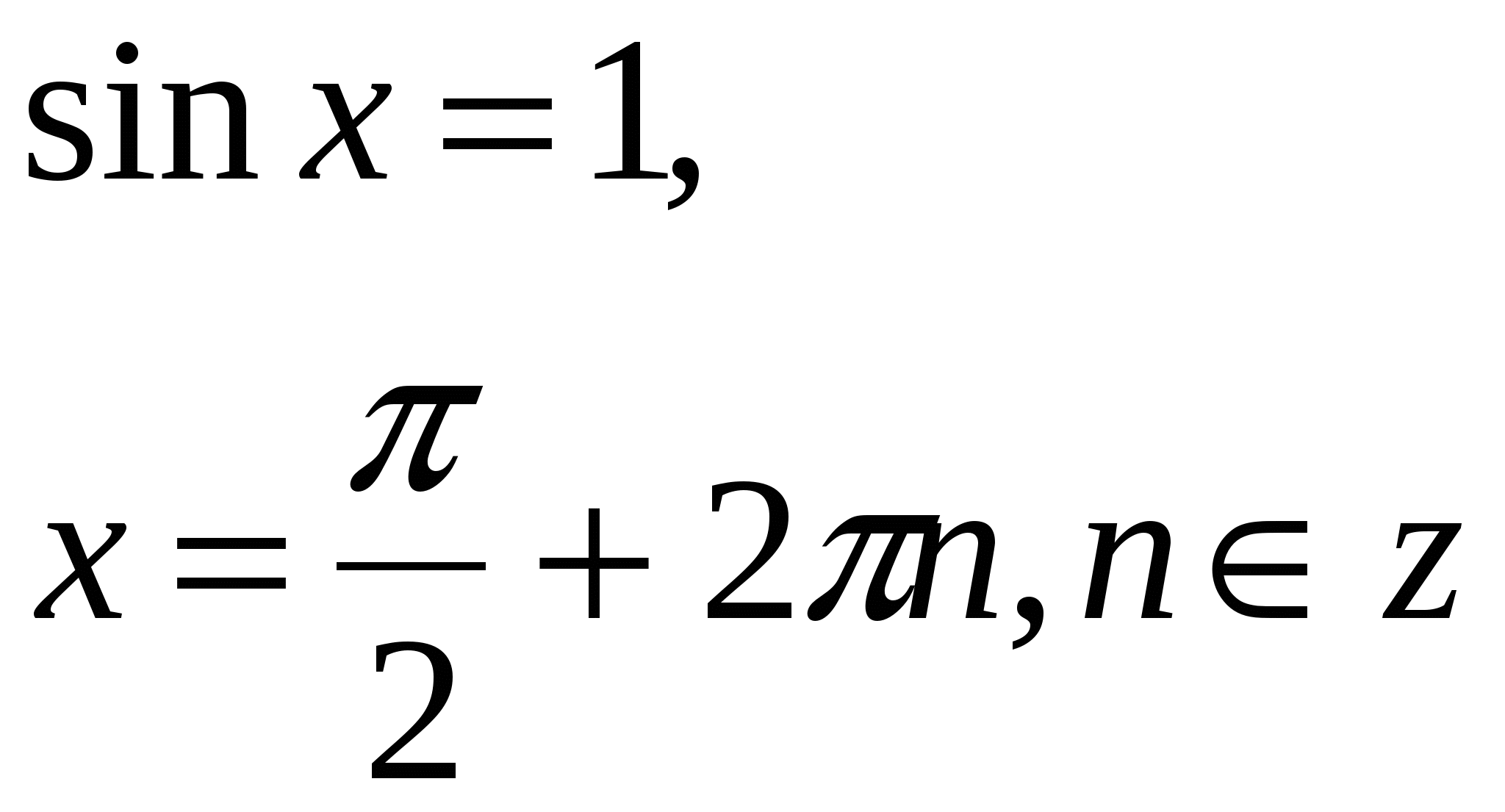
Решить уравнения:

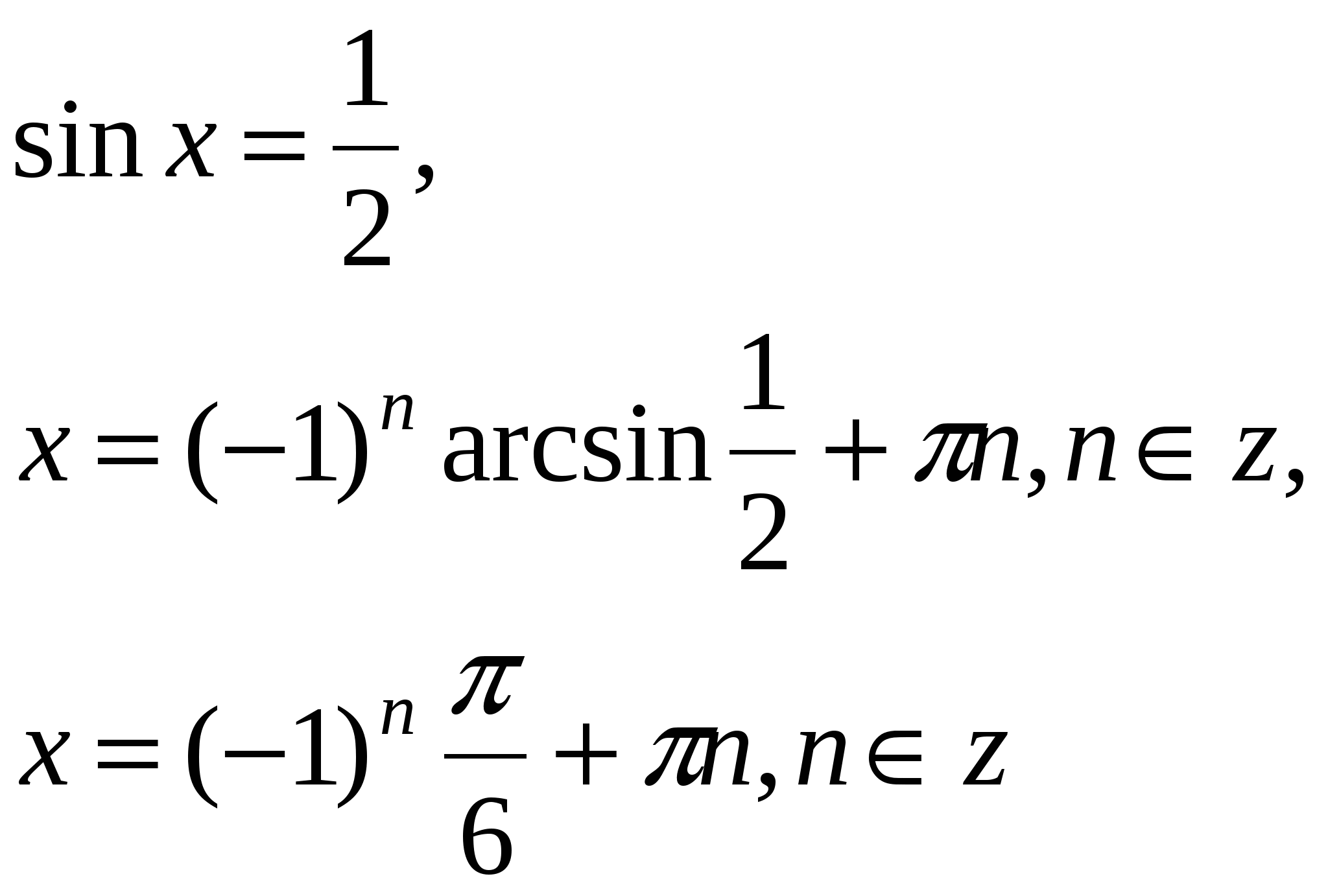
Ответ: .

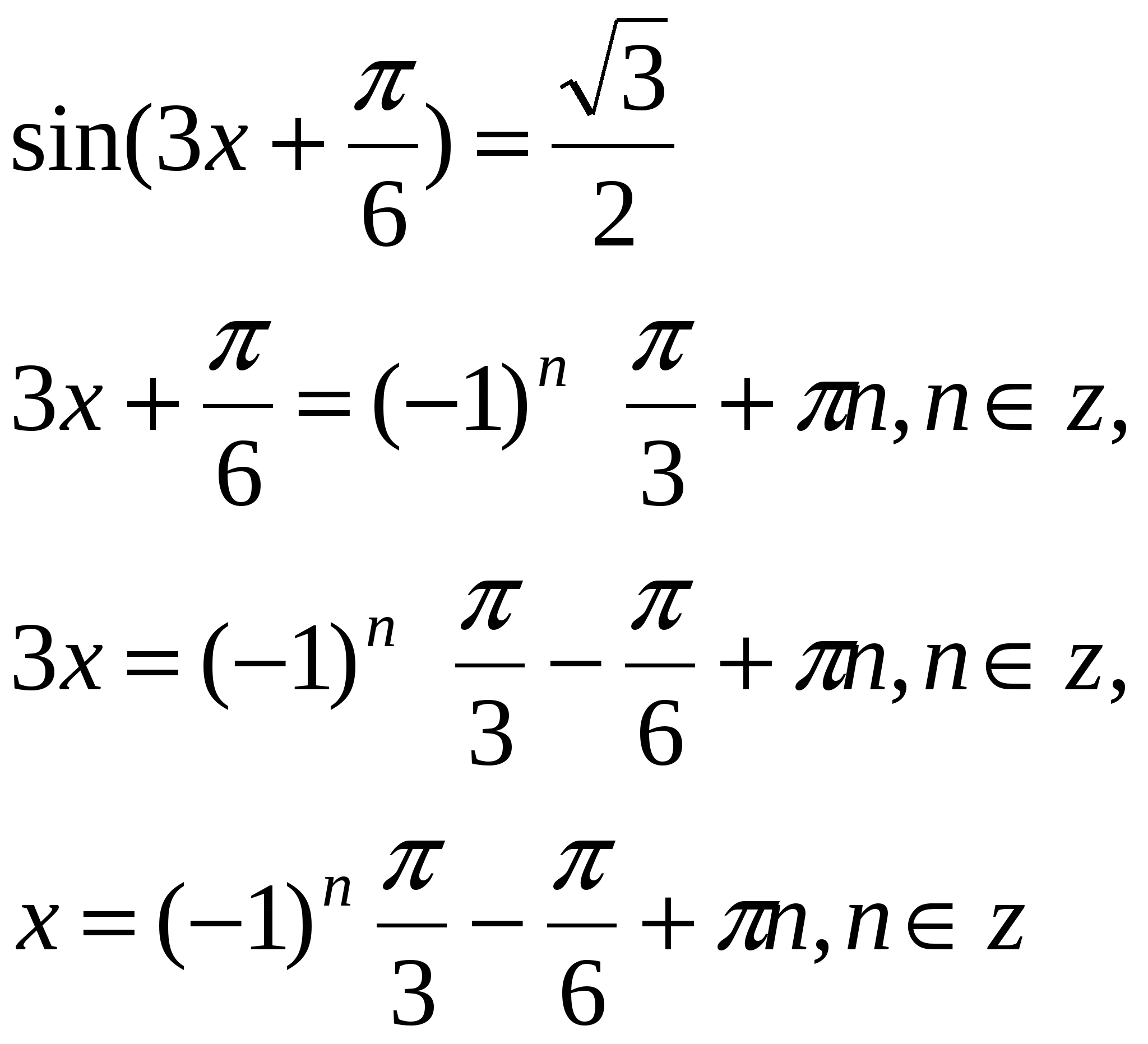
Ответ: .

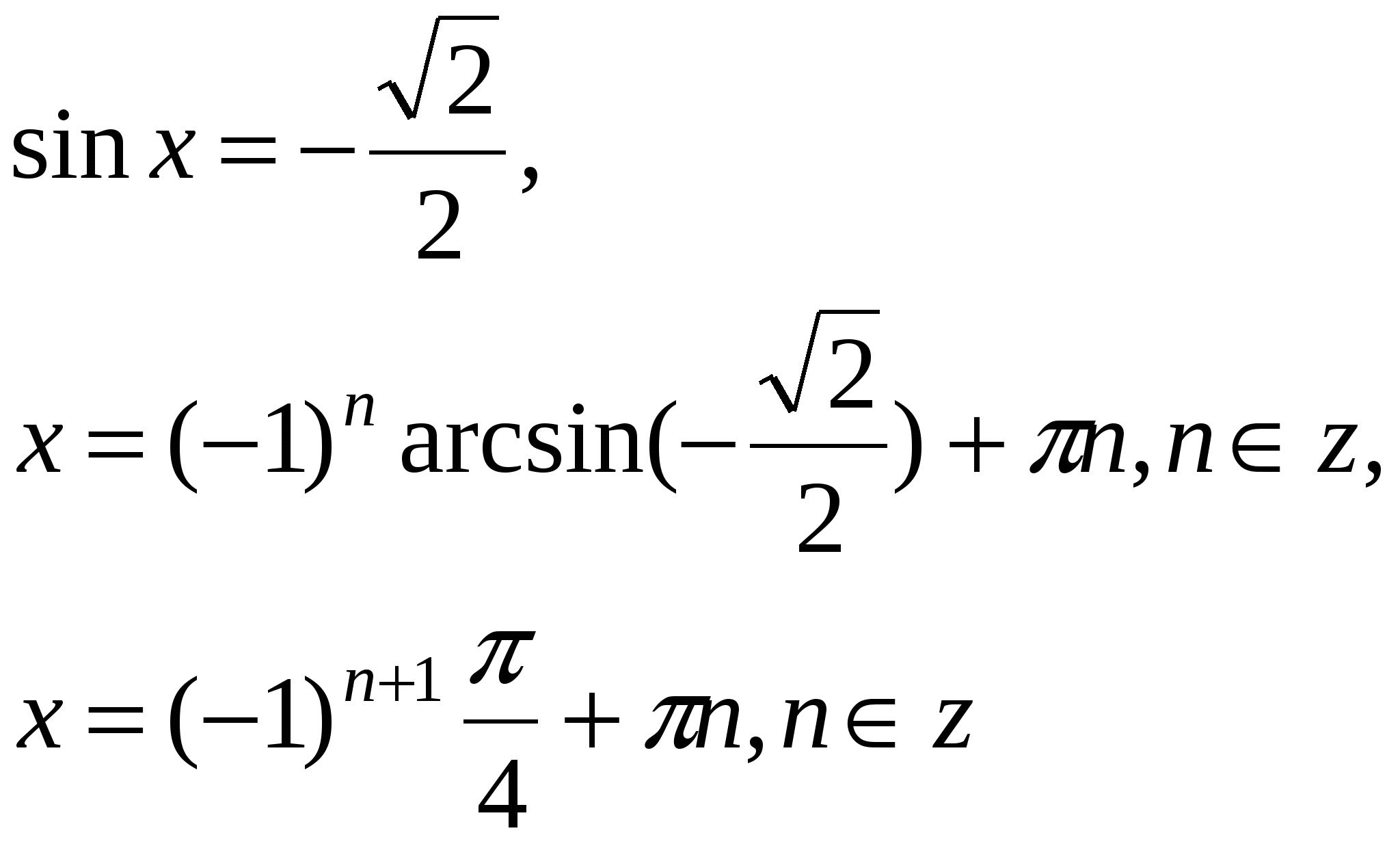
Ответ: .

Решите самостоятельно и найдите правильный ответ(найти соответствие):

№ уравнения

Уравнение

№ ответа

Ответ

1

a

2

b

3

c

4

d

5

e

2.Решение простейших тригонометрических уравнений вида:

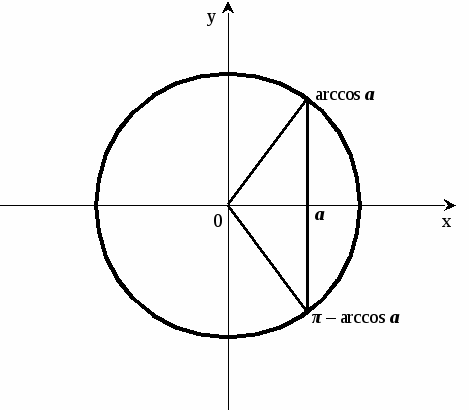, где

если , то

Частные случаи:

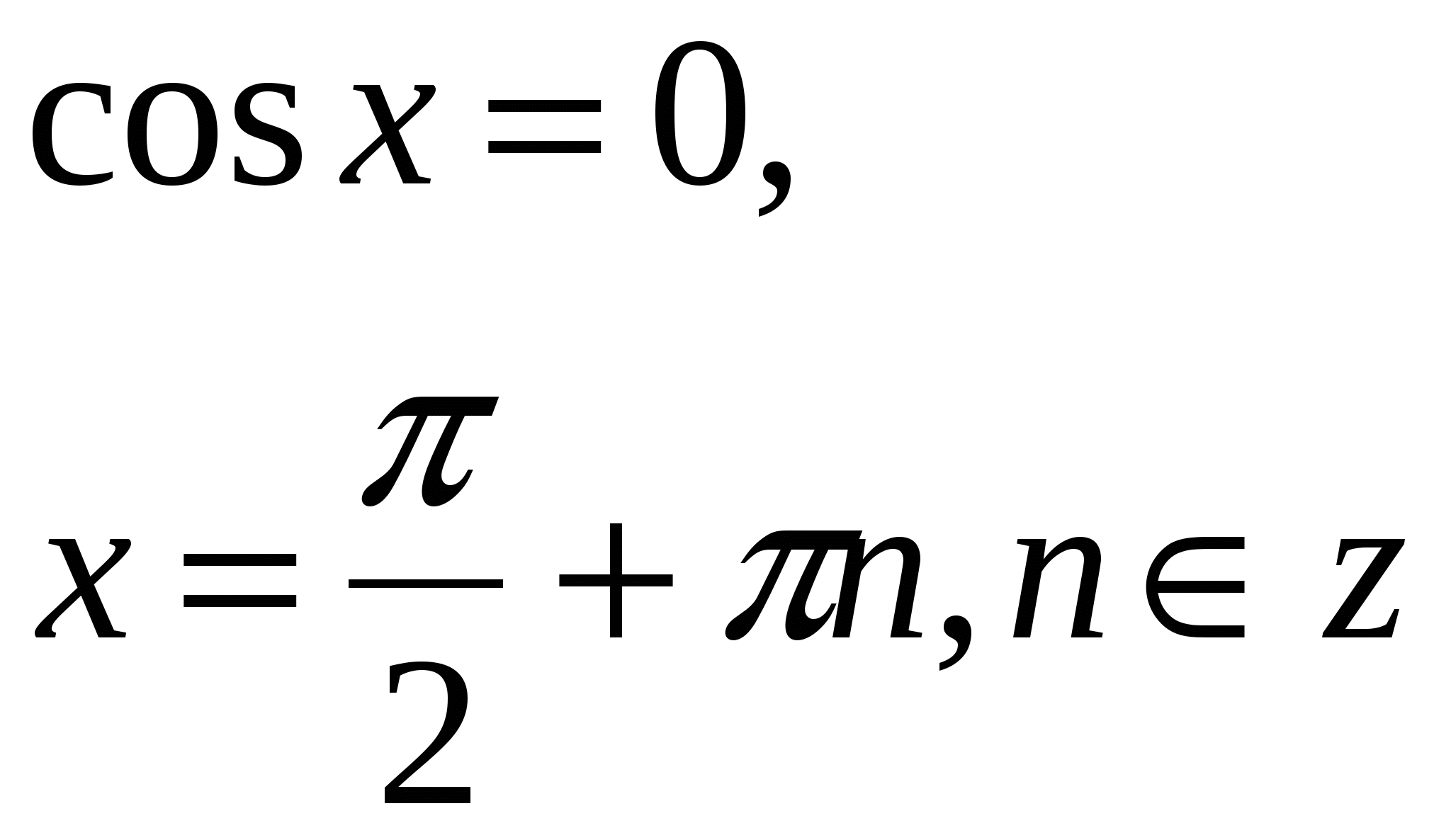
Решить уравнения:

1.

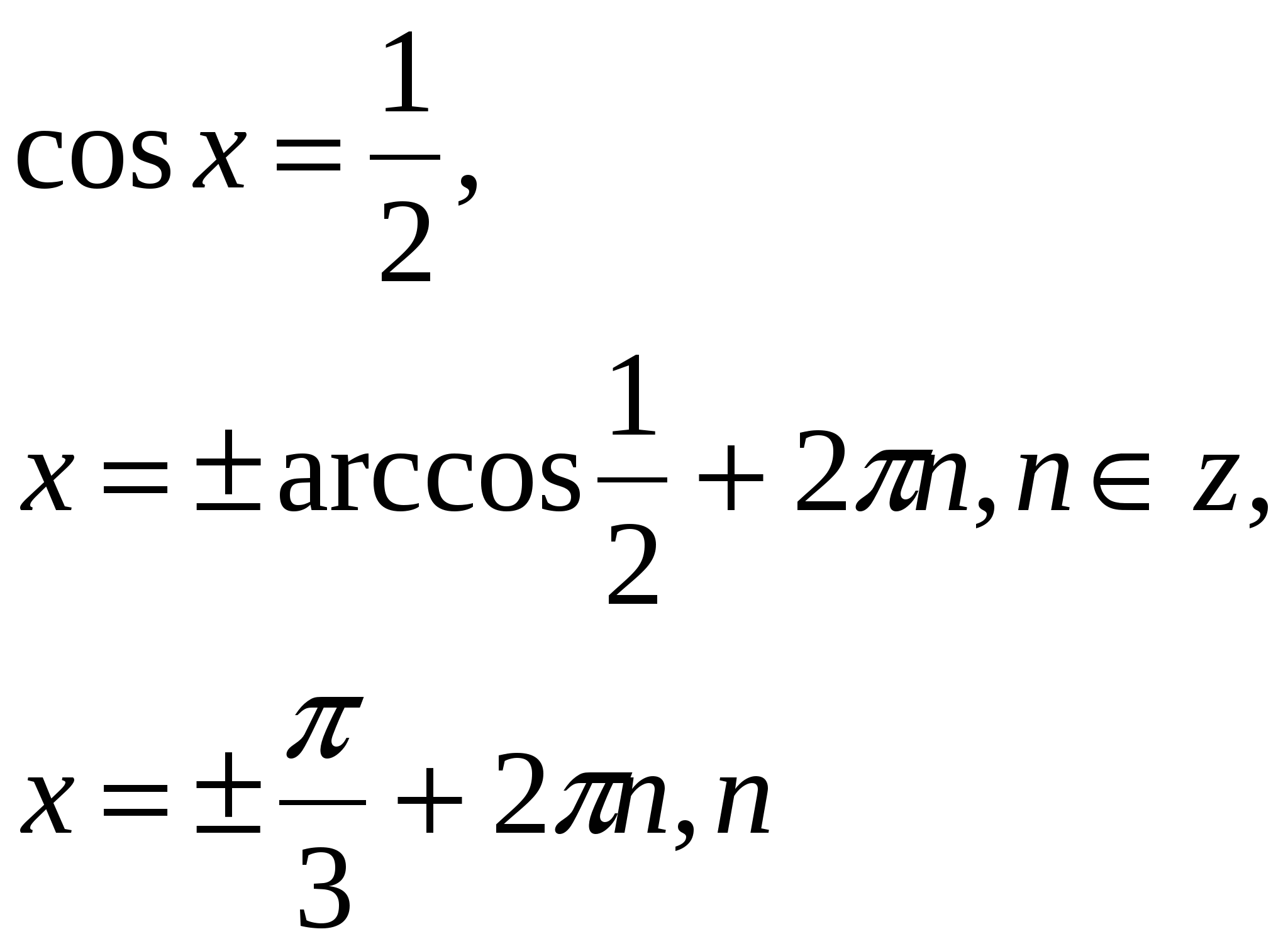
Ответ: .

2.

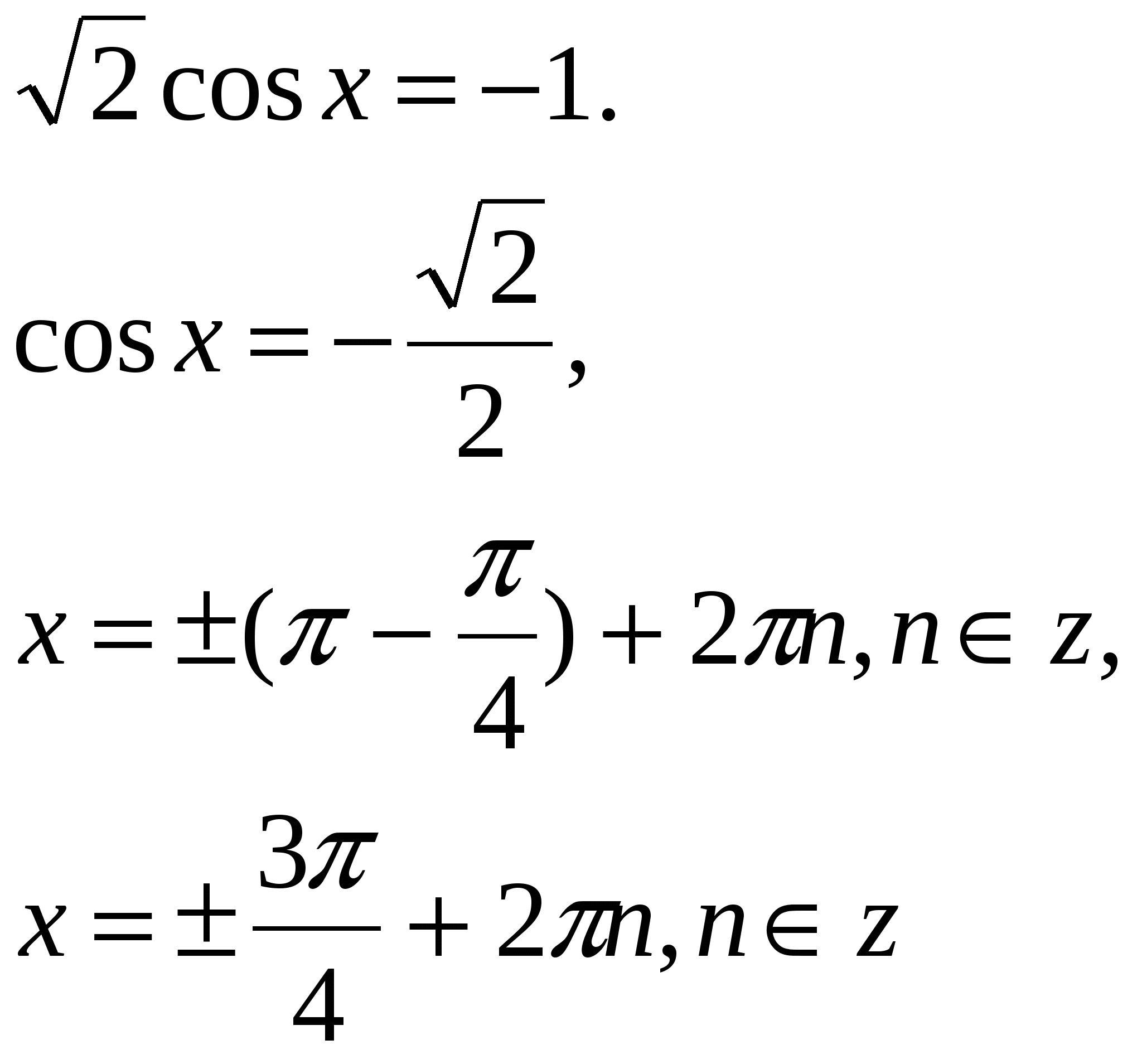
Ответ: .

3.

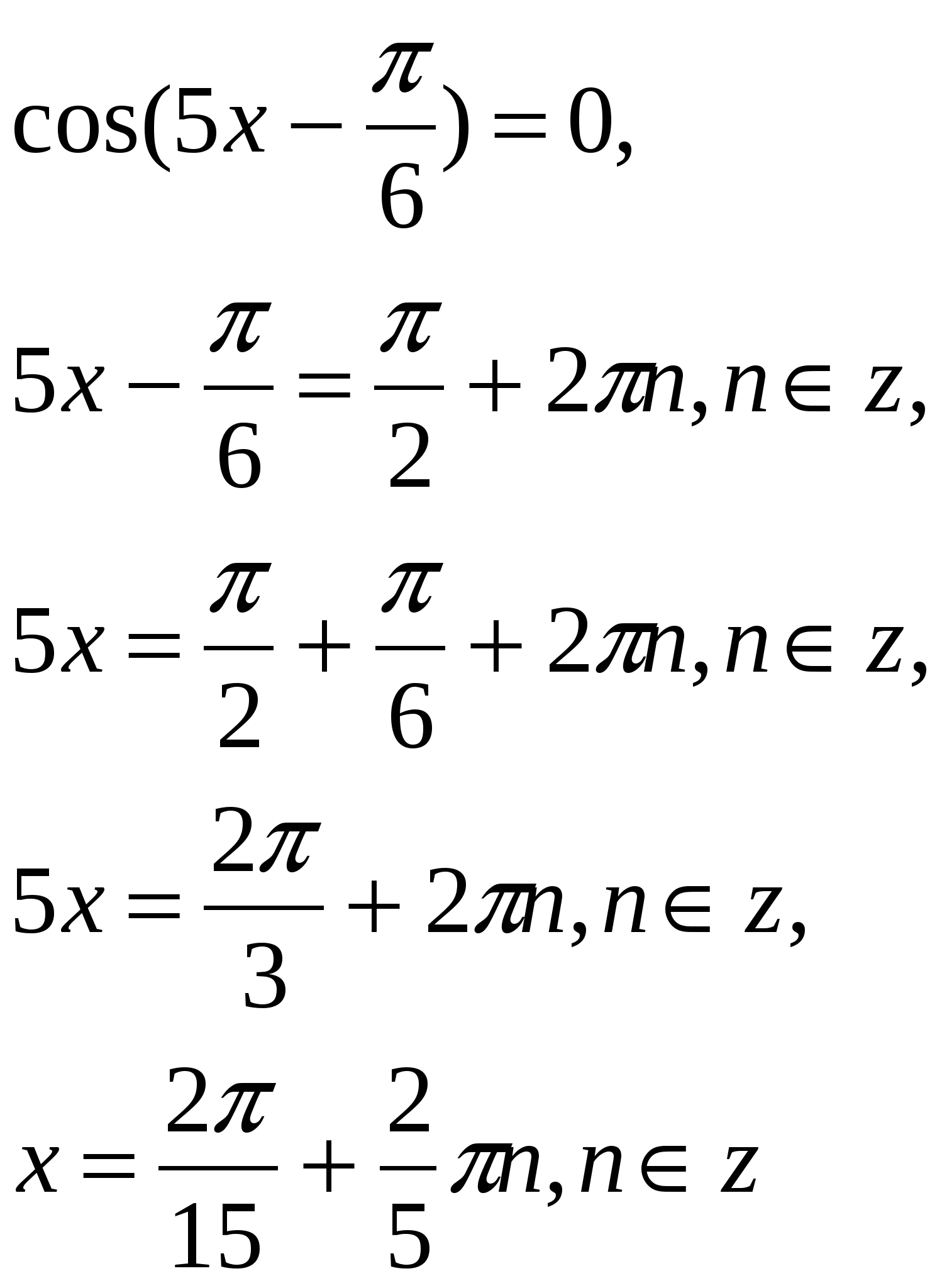
Ответ: .

Решите самостоятельно и найдите правильный ответ (найти соответствие):

№ уравнения

Уравнение

№ ответа

Ответ

a

b

корней нет

c

d

e

3.Решение простейших тригонометрических уравнений вида:

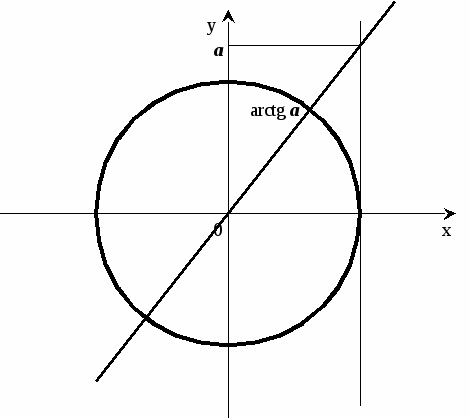
Решить уравнения:

1.

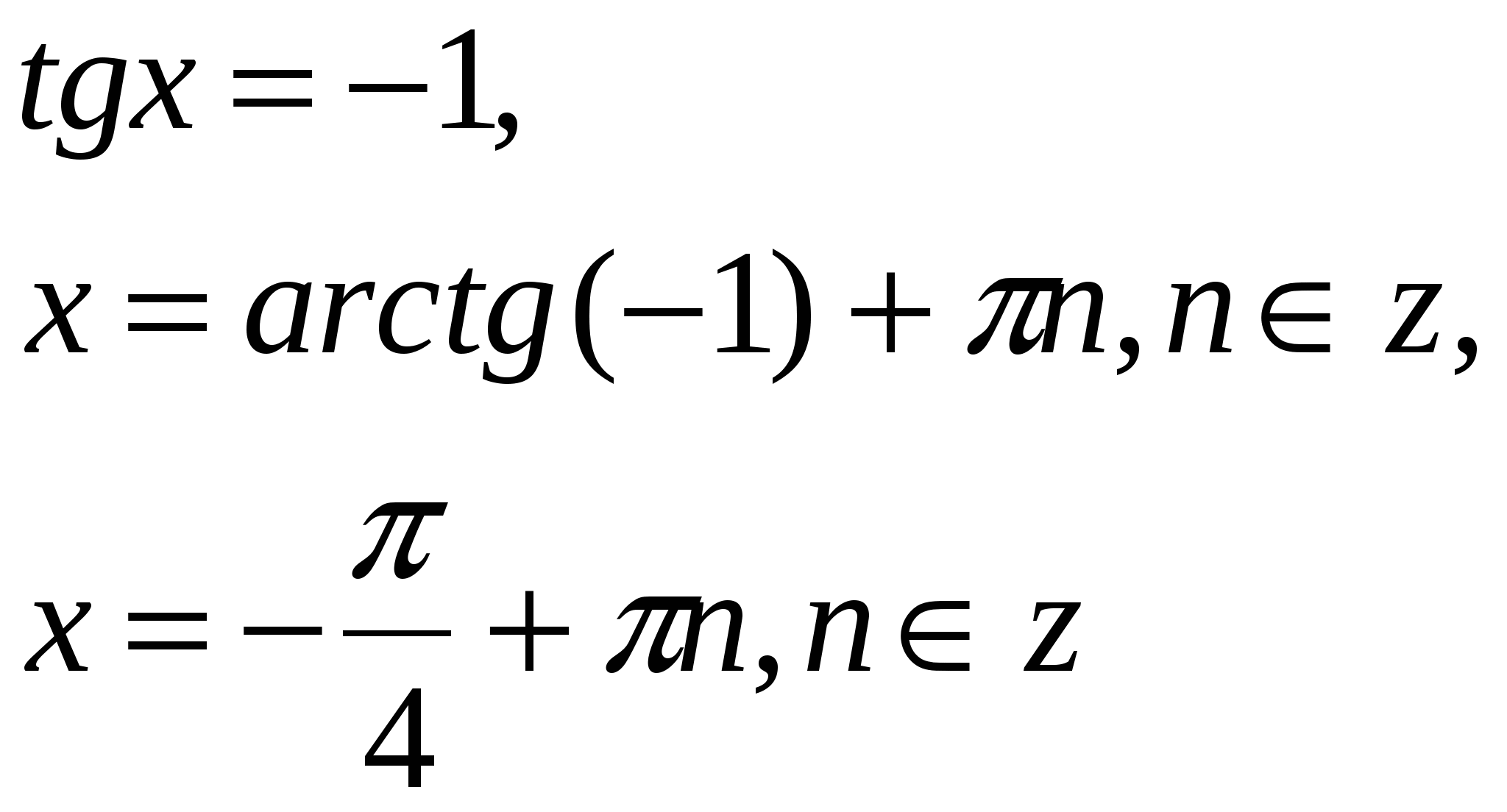
Ответ: .

2.

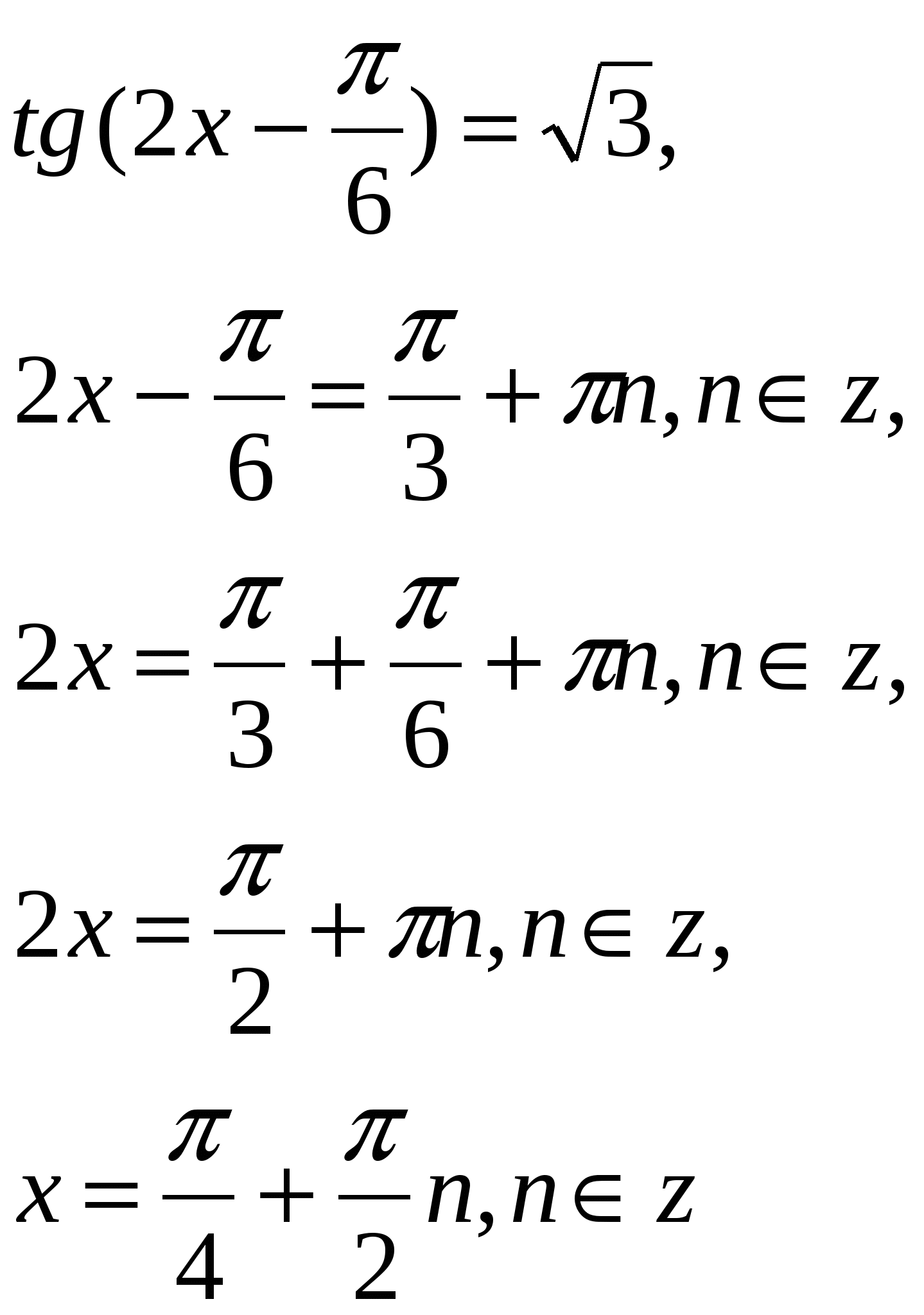
Ответ: .

3.

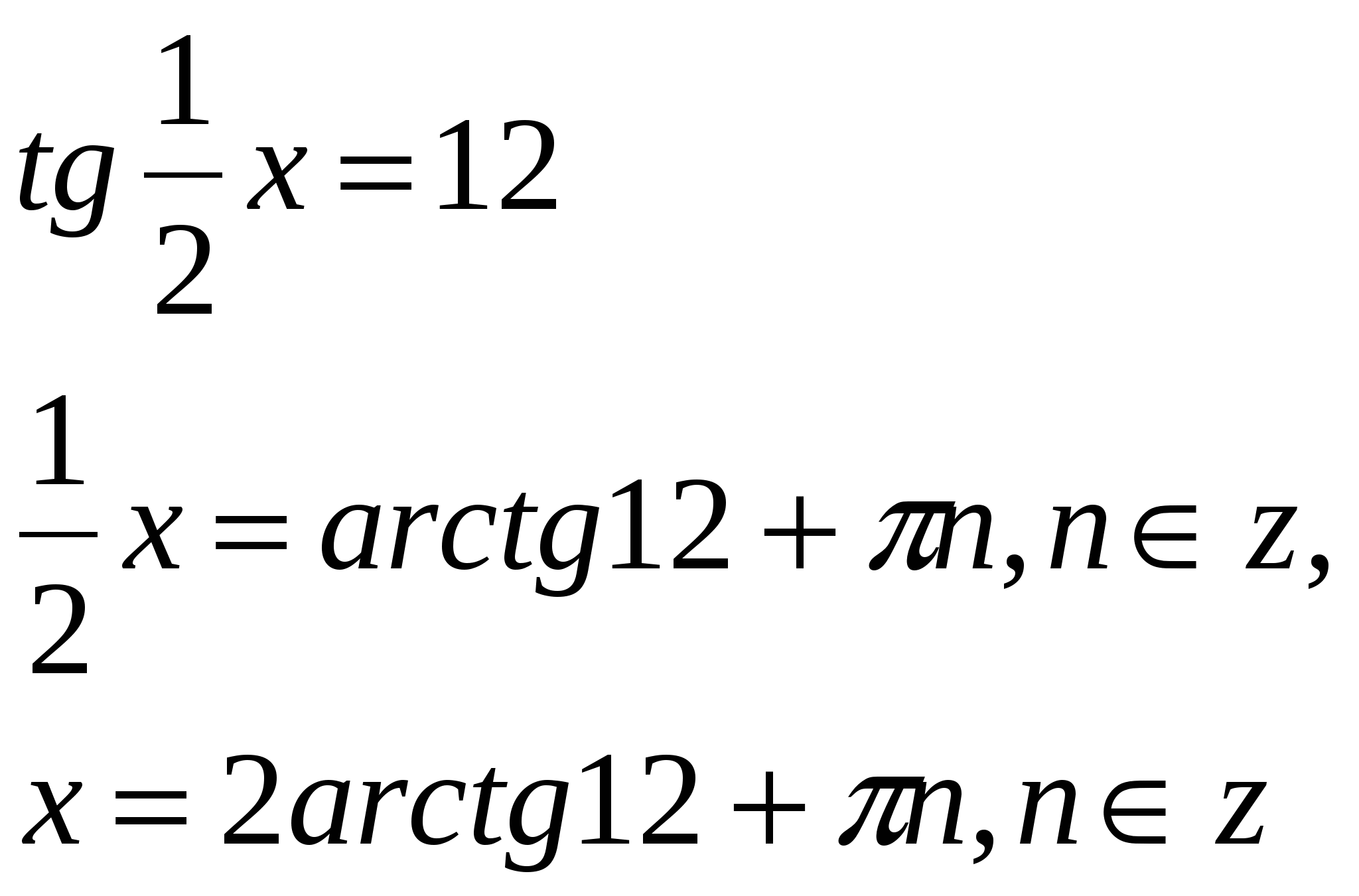
Ответ: .

Решите самостоятельно и найдите правильный ответ (найти соответствие)

№ уравнения

Уравнение

№ ответа

Ответ

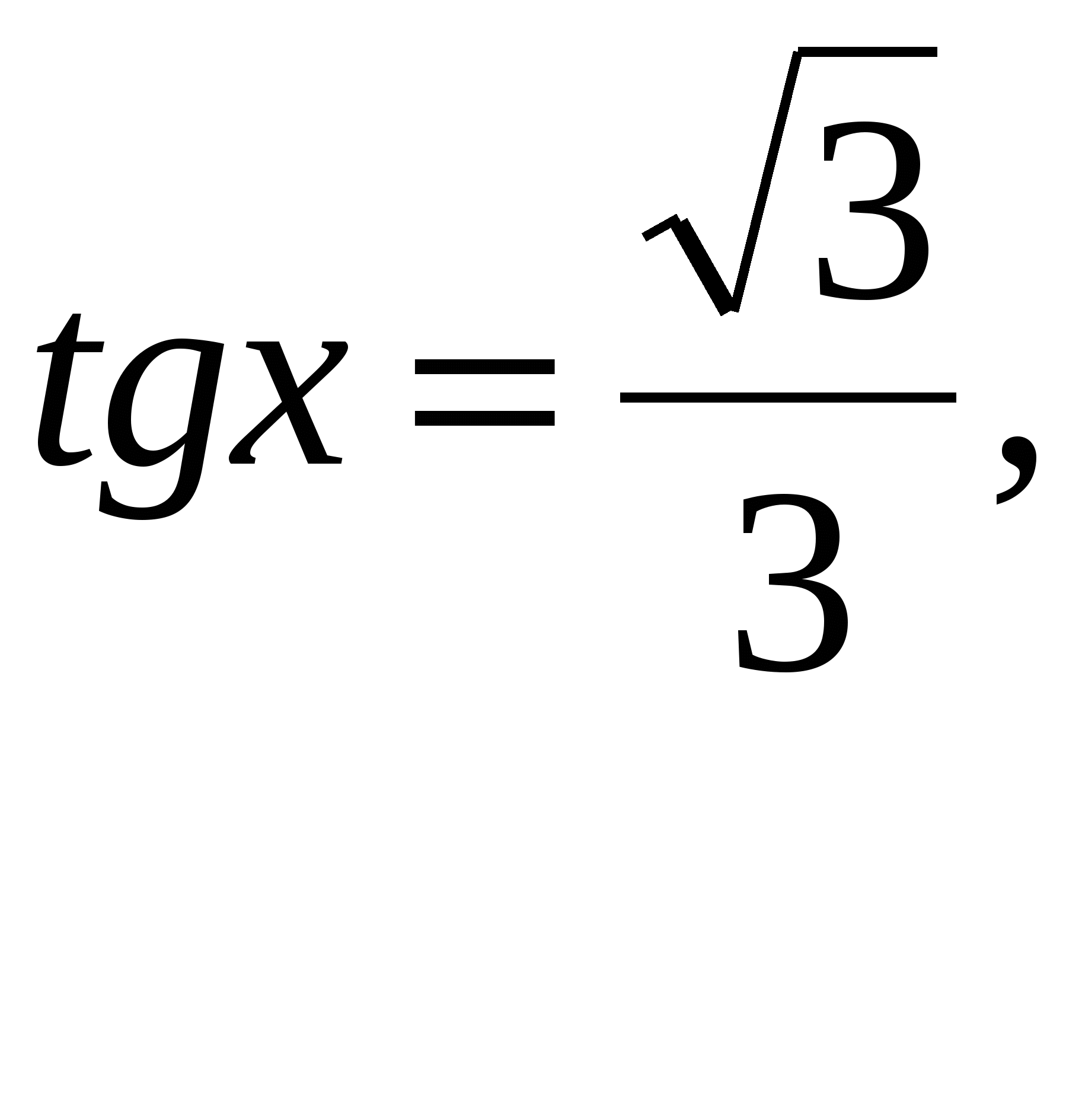
a

b

c

d

Решение простейшего тригонометрического уравнения вида:

решение аналогичное предыдущему случаю.

4.Итог урока:

Сегодня на уроке мы повторили решение простейших тригонометрических уравнений. На следующем уроке будем повторять методы решения тригонометрических уравнений, для этого класс разбивается на 7 небольших групп, каждая из которых покажет выбранный метод решения уравнения:

.

Можно обращаться за консультацией.

Дома повторить пункты № 9,11, учебник под редакцией А.Н.Колмогорова, стр. 93-106, учебник под редакцией А.Г.Мордковича.

Уроки №2-3: «Семинар по решению одного уравнения несколькими способами»

Класс делится на небольшие группы по 2-3 человека, заранее они получают задания по одному из методов решения уравнений, а затем на уроке показывают своё решение. Остальные учащиеся записывают решение и задают интересующие их вопросы, на которые отвечает данная группа.

ЦЕЛИ УРОКА:

1. систематизировать знания учащихся по теме;

2. показать различные методы решения тригонометрического уравнения на примере одного уравнения;

3. воспитание у учащихся культуры мышления;

4. формирование умений строить логическую цепочку рассуждений;

5. показать красоту решения уравнений.

ПЛАН УРОКА:

1. Решение тригонометрических уравнений различными способами;

   1. Используя формул половинного угла;

   2. Используя формулы приведения

   3. Приведение к однородному квадратному уравнению;

   4. Введение вспомогательного угла;

   5. Используя формулы понижение степени;

   6. Используя универсальные подстановки;

   7. Решение уравнения возведением в квадрат;

2. Итог урока.

ХОД УРОКА :

1. Постановка целей урока и конечного результата (каждая группа объясняет свое решение, используя кодоскоп, отвечает на возникшие вопросы).

1.

Используя формул половинного угла.

;

;

;

; или разделим на ;

, ; ;

, . , ;

, .

Ответ: , ; , .

2.

Используя формулы приведения

;

из суммы делаем произведение

;

;

;

;

;

, ;

, ;

, ; , ;

, . , .

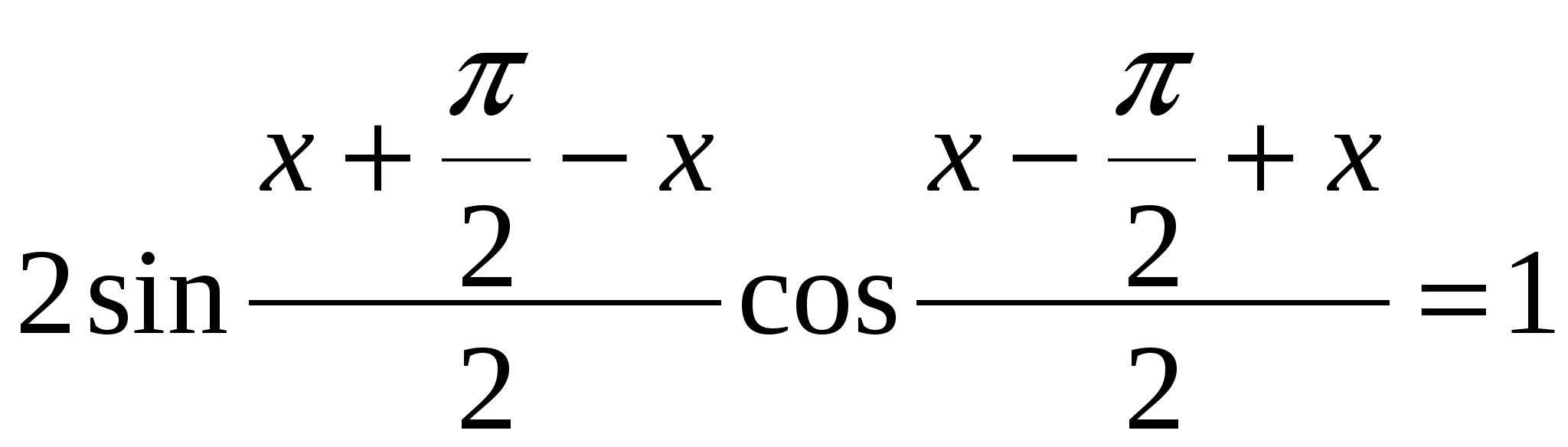Ответ: , ; , .

3.

Приведение к однородному квадратному уравнению.

;

;

;

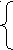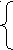; (верно при любых )

;

; или ;

; , .

, .

Оба корня удовлетворяют ОДЗ.

Ответ: , ; , .

4.

введение вспомогательного угла

;

;

;

;

, ;

, ;

если , то

, ;

, ;

если , то

, ;

, ;

, .

Второй способ:

разделим на :

;

;

;

, ;

, или , .

Ответ: , ; , .

5.

Используя формулы понижение степени:

;

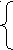Проверка ОДЗ: ;

;

;

.

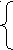
Возведем уравнение в квадрат:

, умножим на 2;

;

;

;

;

; или ;

, ; , ;

, ; , .

Если -нечетное, , то ;

-1=1 – неверно .

Если -нечетное, , то ;

;

-1=1 – неверно.

Если k – чётное, , то ,

следовательно ,

1=1 верно

если n – чётное, ,то ,

следовательно ,

1=1 верно.

Ответ: , ; , .

6.

Используя универсальные подстановки:

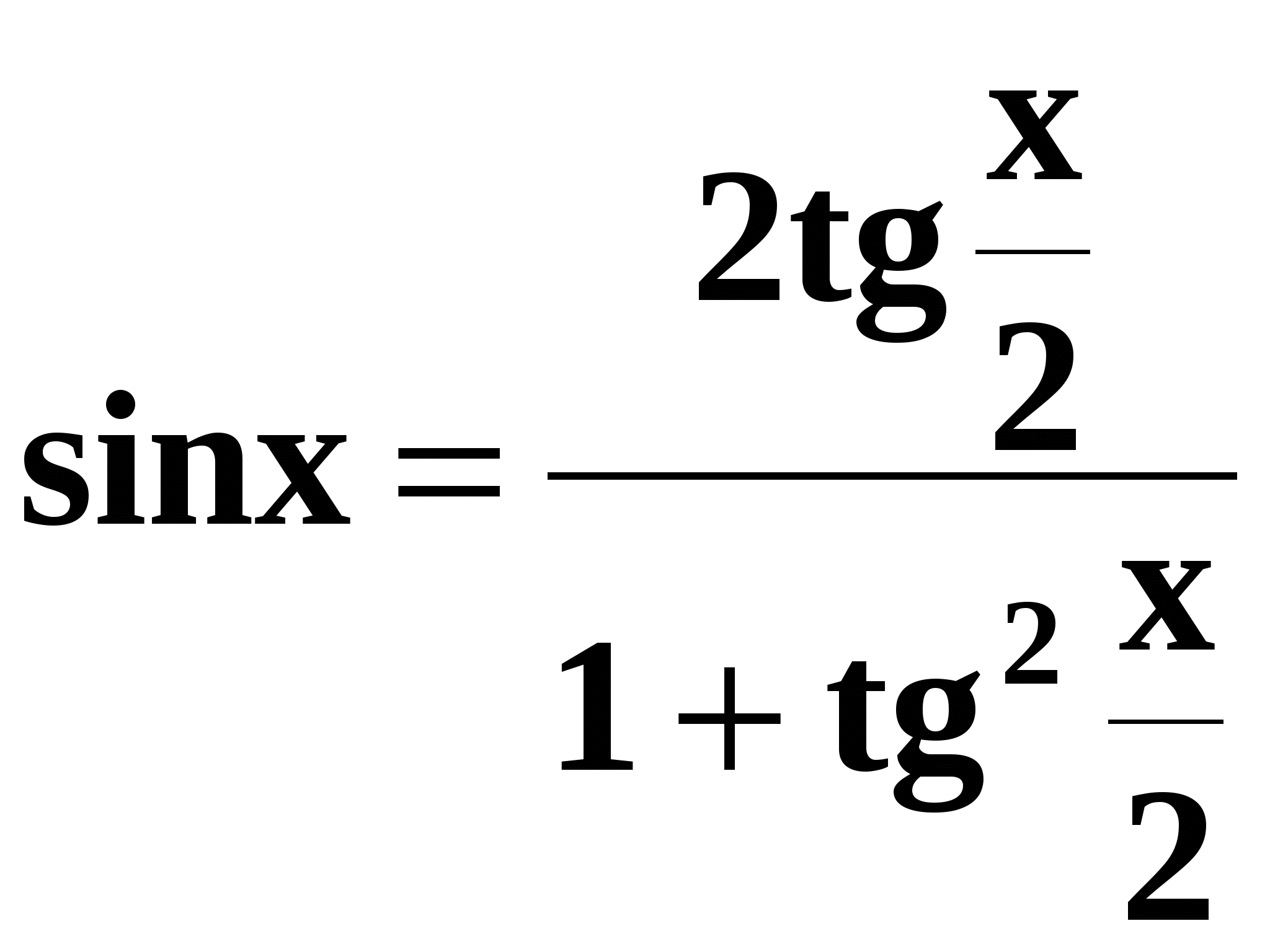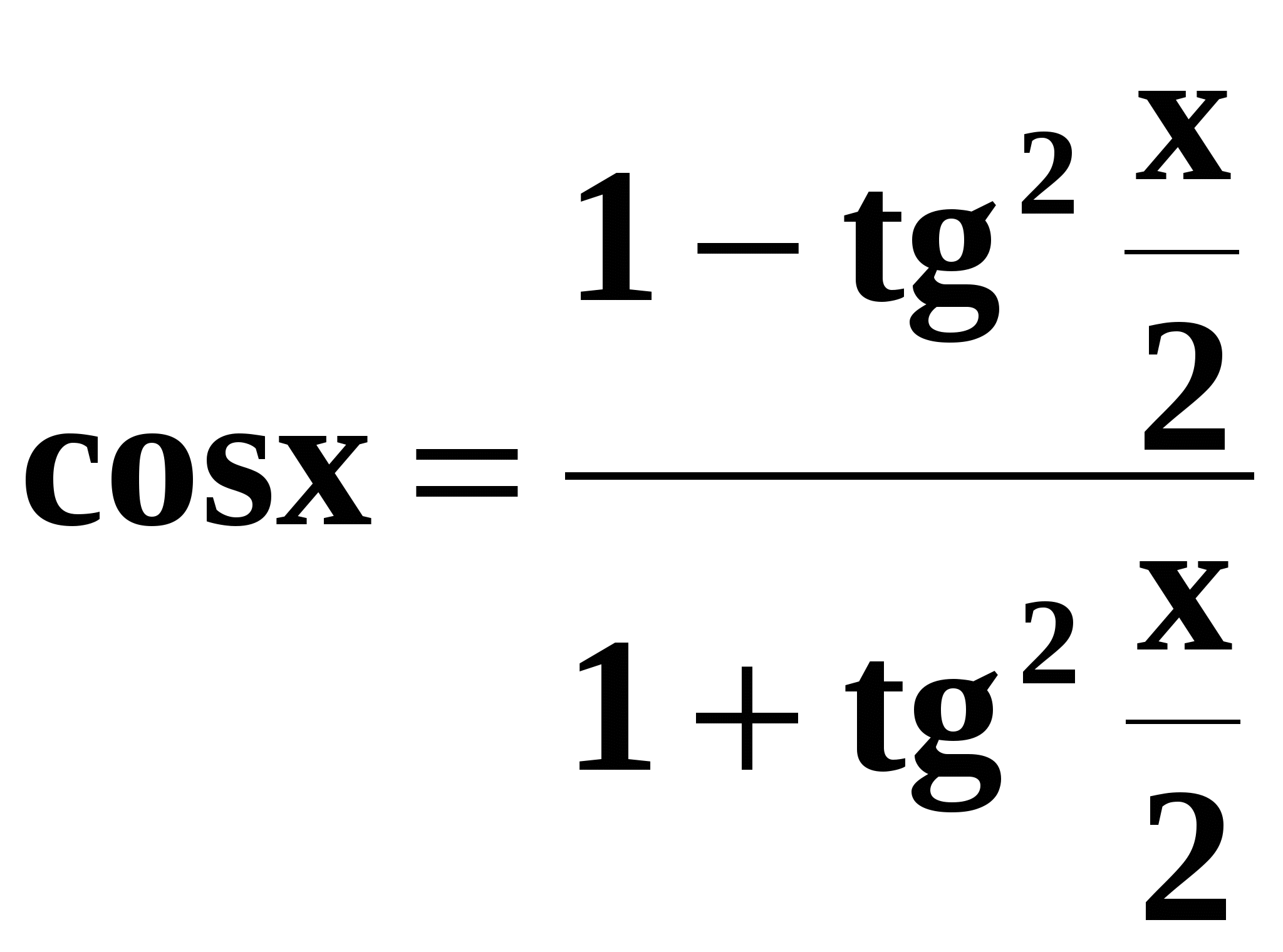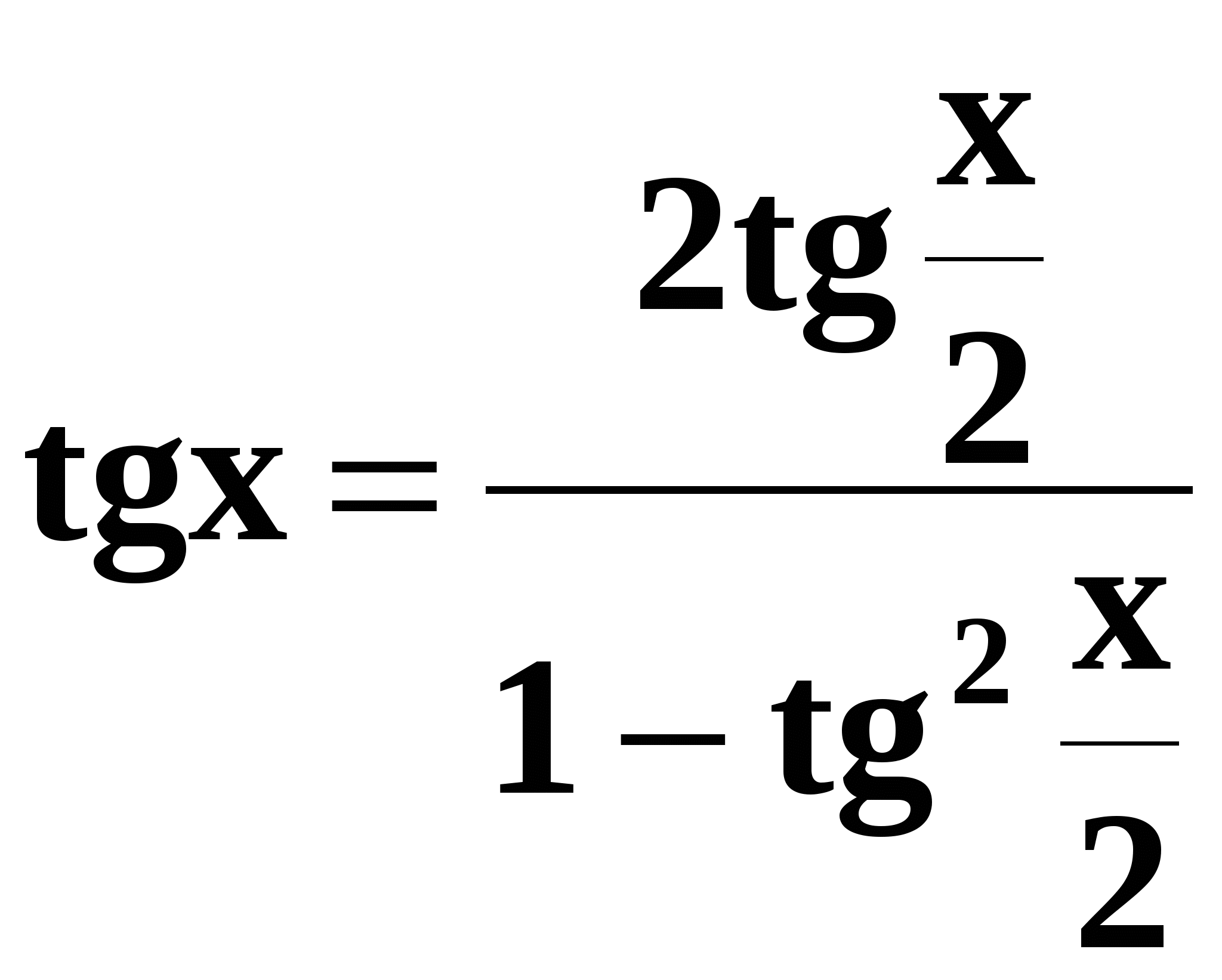; ; , при .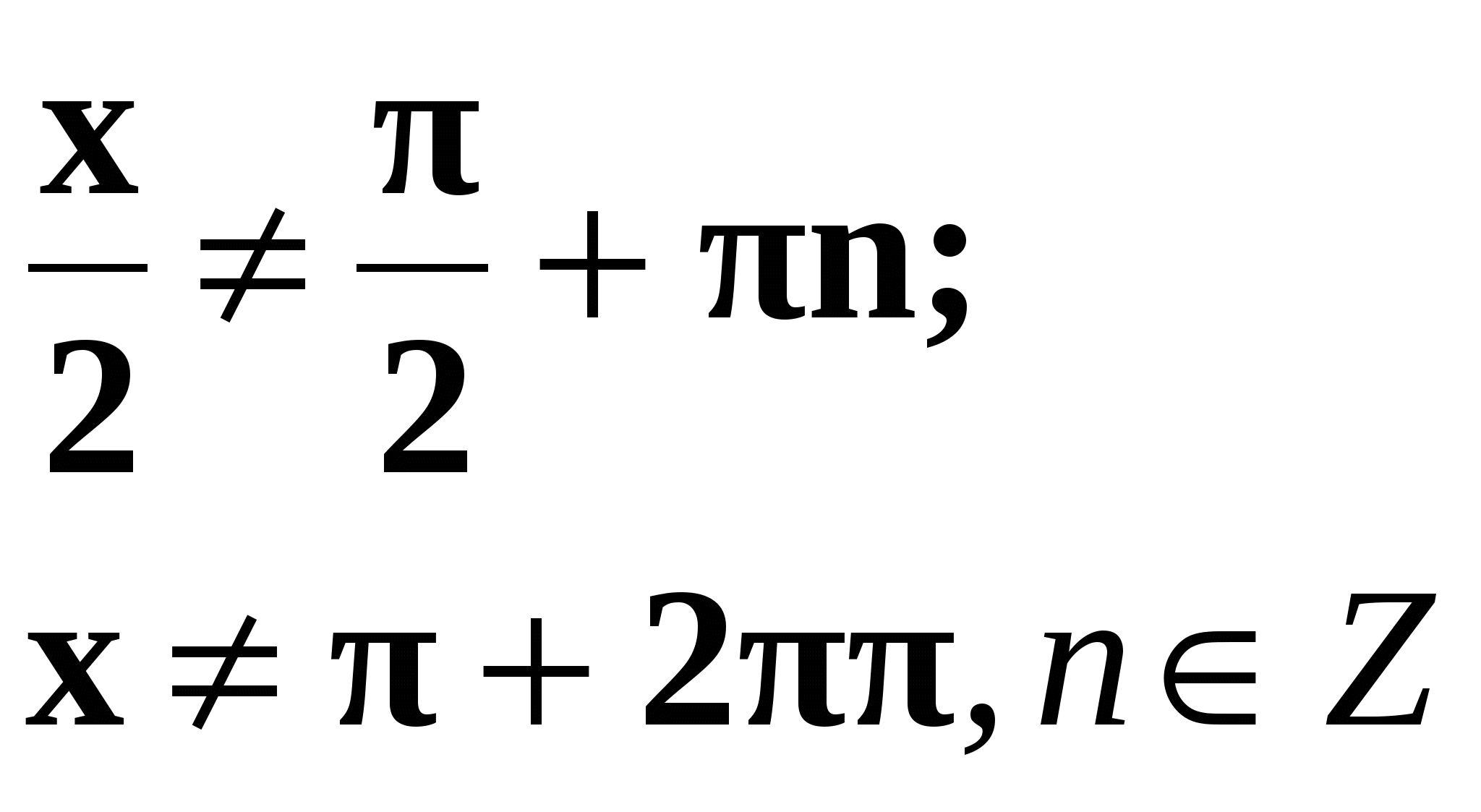

Применение этой подстановки требует большой осторожности! Следует проверить, а не является ли серия корней , корнями данного уравнения (иначе будет потеря корней). Это делается путем подстановки в первоначальное уравнение.

;

Если , , то ;

;

;

– неверно.

Следовательно , не является корнем уравнения.

Выполним подстановку:

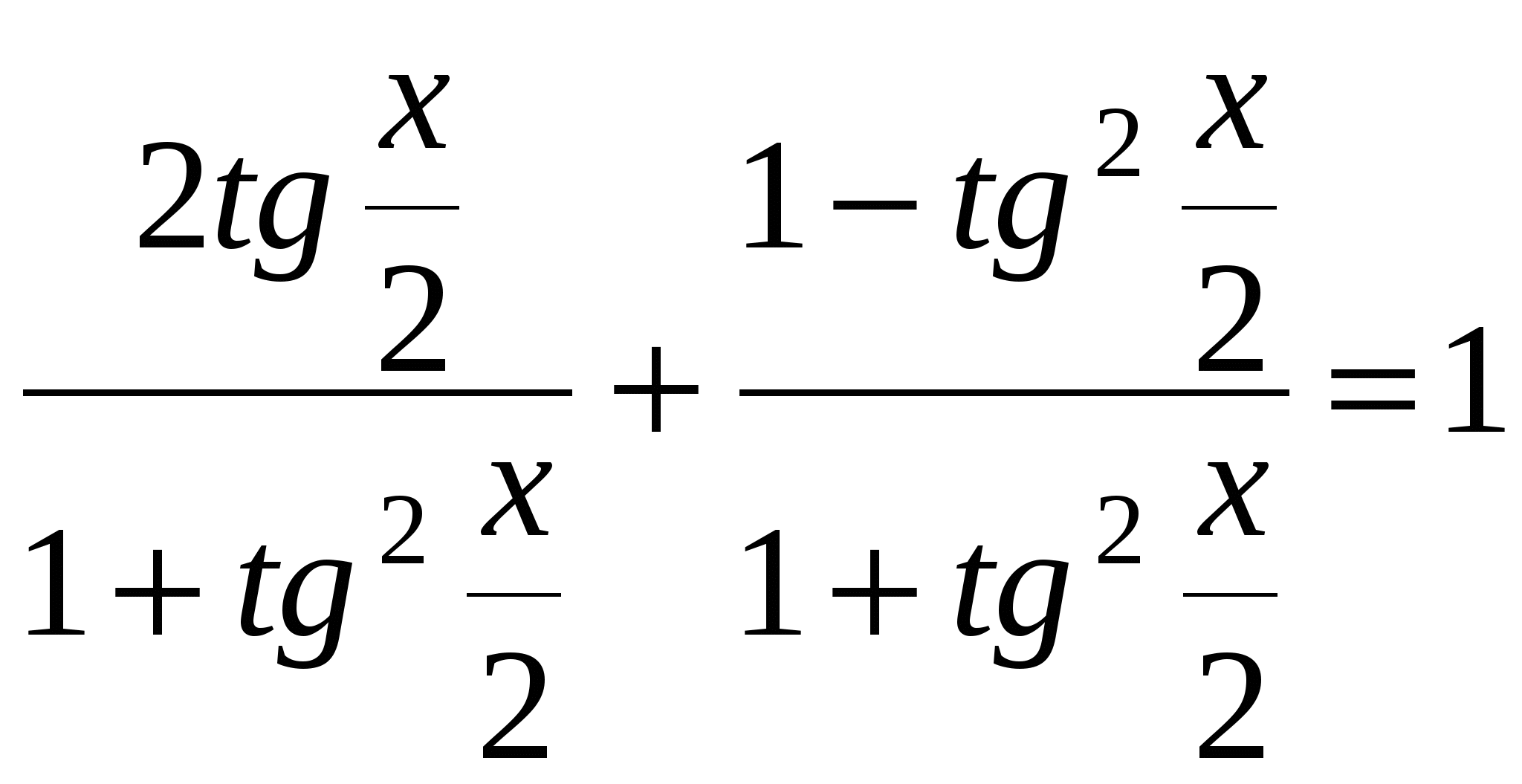, пусть ;

;

;

;

; или ;

; ;

, ; , ;

, . , .

Ответ: , ; , .

7.

Решим уравнение возведением в квадрат. Надо быть аккуратными – могут появиться лишние корни.

;

;

;

;

;

, ;

, .

Проверка корней:

Если ; ;

;

1=1 – верно;

; ;

;

1=1 – верно;

; ;

;

-1=1 – неверно;

; ;

-1=1 – неверно;

Ответ: , ; , .

ИТОГ УРОКА:

• Сегодня на уроке мы с вами решили одно уравнение семью способами и это ещё не предел методов решения. При решении уравнений вы можете использовать один из предложенных способов, самое главное каждое уравнение имеет решение и его надо найти!

• оценивается работа каждого учащегося, подчеркивается самостоятельность, грамотность при выполнении заданий, взаимопомощь, активность.

ЗАДАНИЕ НА ДОМ:

Решите уравнение всеми предложенными способами и попытайтесь найти ещё хотя бы один другой способ решения.

Уроки №4-5: «Решение более сложных уравнений, предложенными способами»

ЦЕЛИ УРОКА:

1. обобщить полученные знания;

2. научить нахождению чужих ошибок и не делать своих;

3. показать красоту решения тригонометрических уравнений.

ПЛАН УРОКА:

1. Разбор ошибок (с использованием кодоскопа);

2. Решение тригонометрических уравнений различными способами;

   1. Решение уравнений разложением на множители;

   2. Решение с помощью замены переменных;

   3. Решение однородных уравнений;

   4. Решение уравнений методом преобразования суммы или разности тригонометрических выражений в произведения;

   5. Преобразование произведения в сумму;

   6. Введение вспомогательного угла;

   7. Решение линейных уравнений;

   8. Уравнения, решающие оценкой значений левой и правой частей;

   9. Комбинированные уравнения из заданий ЕГЭ.

3. Итог урока.

1.   Разбор ошибок (с использованием кодоскопа)

1.   sinx=0.5

x=(-1)ⁿarcsin0.5+2n,

x=(-1)^{n +} ,.

2.   cos3x=0.5

3x=arccos0.5+2n, ,

3x= +2 n, ,

x= .

3.   sin4x=2

4sinx=2,

sinx=0.5,

x=(-1)ⁿarcsin0.5+ n, ,

x=(-1)ⁿ⁺ .

4.   tg2x=5

2x=arctg5+ n, ,

x=arctg2.5+ n, .

2.   Решение тригонометрических уравнений различными способами.

1.   Решение уравнений разложением на множители:

а)   sin2x-cosx=0,

2sinx cosx cos x=0,

cosx(2sin x – 1 =0,

2sin x-1 =0 или cos x =0

sinx=0.5 x=+ k, .

x=(-1)ⁿ+ n, .

Ответ: (-1)ⁿ+ n, , + k, .

Для домашней работы: sinx+cosx=sinxcosx + 1

2.   Решение с помощью замены переменных:

а)   6cos ²x+5sinx-7=0,

6(1-sin ²x)+5sinx-7=0,

6-6sin ²x +5sinx-7=0, sinx=t, ItI 1,

6t² -5t+1=0,

t= t=

sinx= или sinx =0.5

x=(-1)ⁿarcsin + n, x=(-1)^k + k,

Ответ: (-1)ⁿarcsin + n, , (-1)^k + k,

Для домашней работы: 1) cos ²x + cosx – 2=0;

2) tg ²x – 3tgx + =0.

б)   sin ⁴x+cos ⁴x – 2sin2x + sin ²2x=0,

прибавим и вычтем 2sin²x·cos²x для выделения полного квадрата

(sin²x + cos ²x)²- 0.5(4sin² xcos²x) + sin²2x - 2sin2x = 0,

1- sin²2x – 2sin2x + sin²2x=0,

sin² 2x – 2sin2x + 1 =0, sin2x = t, -1t1

t² – 8t + 4 = 0,

D=64- 16 = 48 , D>0, 2 корня

t = 4- 2,

t = 4 +2, (не удовлетворяет условию -1t1)

sin2x = 4-2 ,

2x = (-1)^k arcsin(4-2 ) + k,

x = (-1)^karcsin(4 - 2)+ k, .

Ответ: (-1)^karcsin(4 - 2)+ k, .

3.   Решение однородных уравнений

asin x +bcosx = 0

asin ²x + bcosxsinx + c cos ²x = 0

Метод: разделив обе части уравнения на sinx( sin ²x) или на cosx(cos ²x) отличных от нуля, иначе не выполняется основное тригонометрическое тождество, получим уравнение линейное или квадратное относительно новой переменной:

atgx + b = 0, a tg ²x + btgx + c =0

Решим уравнение:

6sin ²x + sinx cosx – cos ²x = 2,

6sin ²x + sinx cosx – cos ²x -2 sin ²x – 2 cos ²x =0,

4sin ²x + sinxcosx -3cos ²x = 0 /Разделим на cosx, cosx отличен от нуля

4tg ²x + tgx – 3 =0

tgx=t,

4t² + t -3=0,

t= -1, t =

tgx = -1, tgx=

x= - + Пn, . x = arctg + Пk, .

Ответ: - + Пn, , arctg + Пk, .

Для домашней работы: sin 5x +cos5x = 0,

3sin ²x – 2sinx cosx – cos ²x = 0.

4.   Решение уравнений методом преобразования суммы или разности тригонометрических выражений в произведения

Необходимо действовать по принципу: «увидел сумму, делай произведение»

cos3x + sin2x – sin4x =0,

cos3x + 2 cossin = 0,

cos3x- 2 cos3x sinx = 0,

cos3x (1 – 2sinx) = 0,

cos3x = 0 sinx = 0.5

3x = + П n, , x= (-1)^k+ Пk, .

x=+ n,

первая серия корней содержит полностью вторую серию корней, следовательно

Ответ: + k, .

5.   Преобразование произведения в сумму:

sin5x cos3x = sin6xcos2x,

0.5(sin2x + sin8x) = 0.5(sin8x + sin4x),

sin2x + sin8x =sin8x + sin4x,

sin2x – sin4x = 0,

-2 sinx cos3x =0,

sinx = 0 cos3x = 0

x = П n, 3x = +П k, ,

x = +П k, .

Ответ: П n, , +П k, .

6.   Введение вспомогательного угла:

(a,b,c отличные от нуля)

; .

Решим следующее уравнение

разделим на (так как )

,

, , .

,

,

, ,

, .

Ответ:

Для домашней работы: 1),

2)

3).

7.   Решение линейных уравнений:

1 способ:

Используя универсальную подстановку: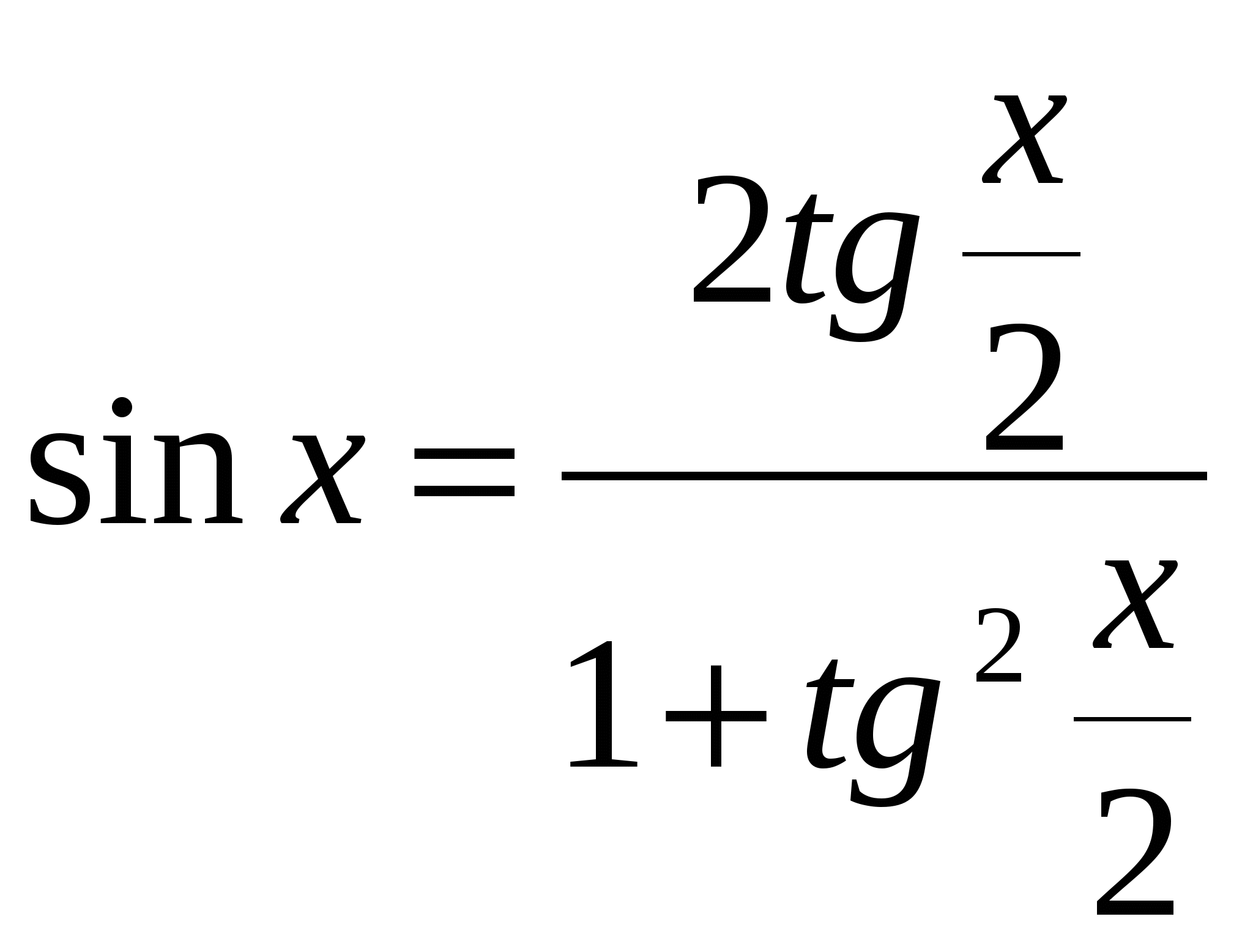, , 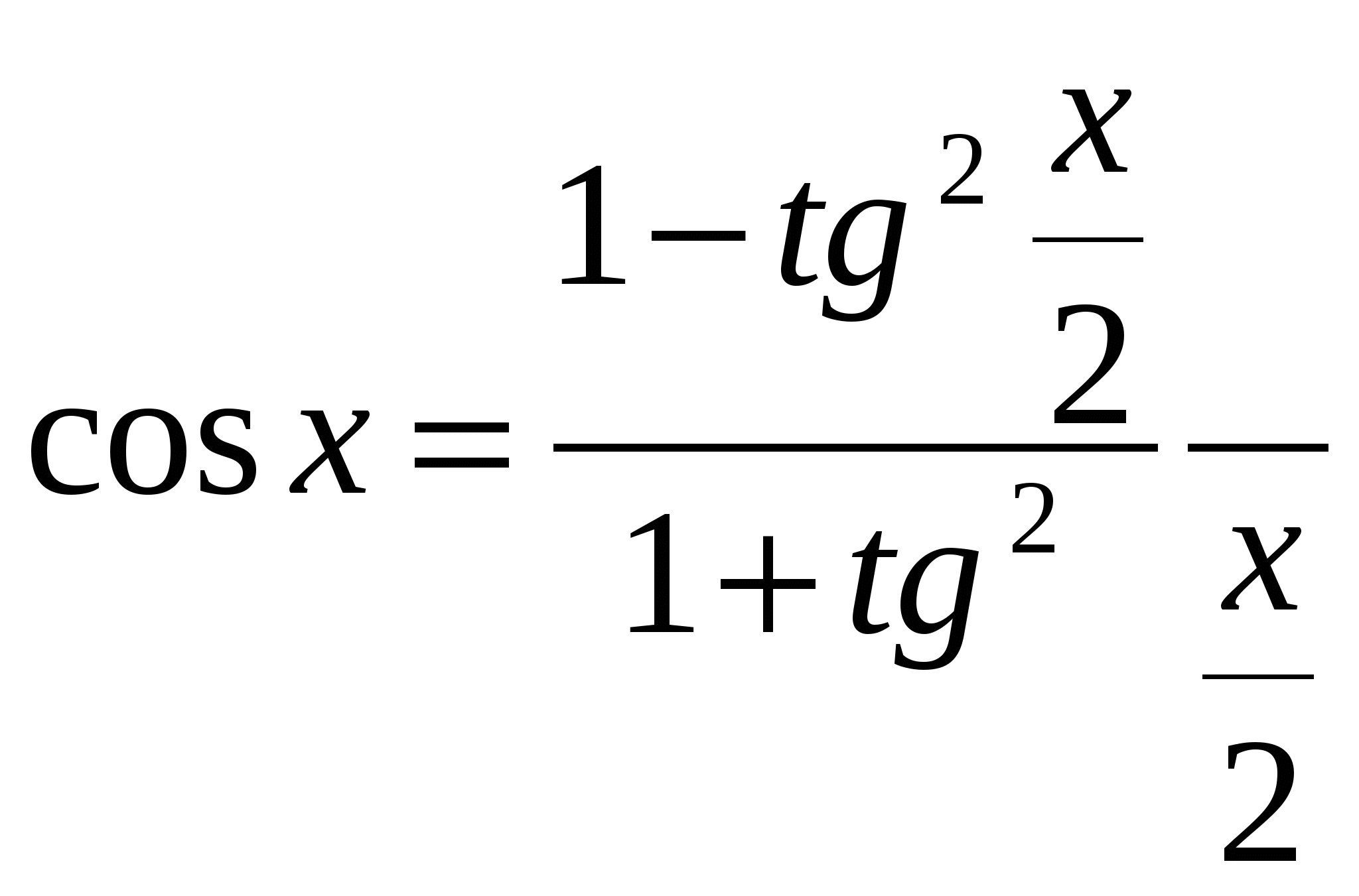, 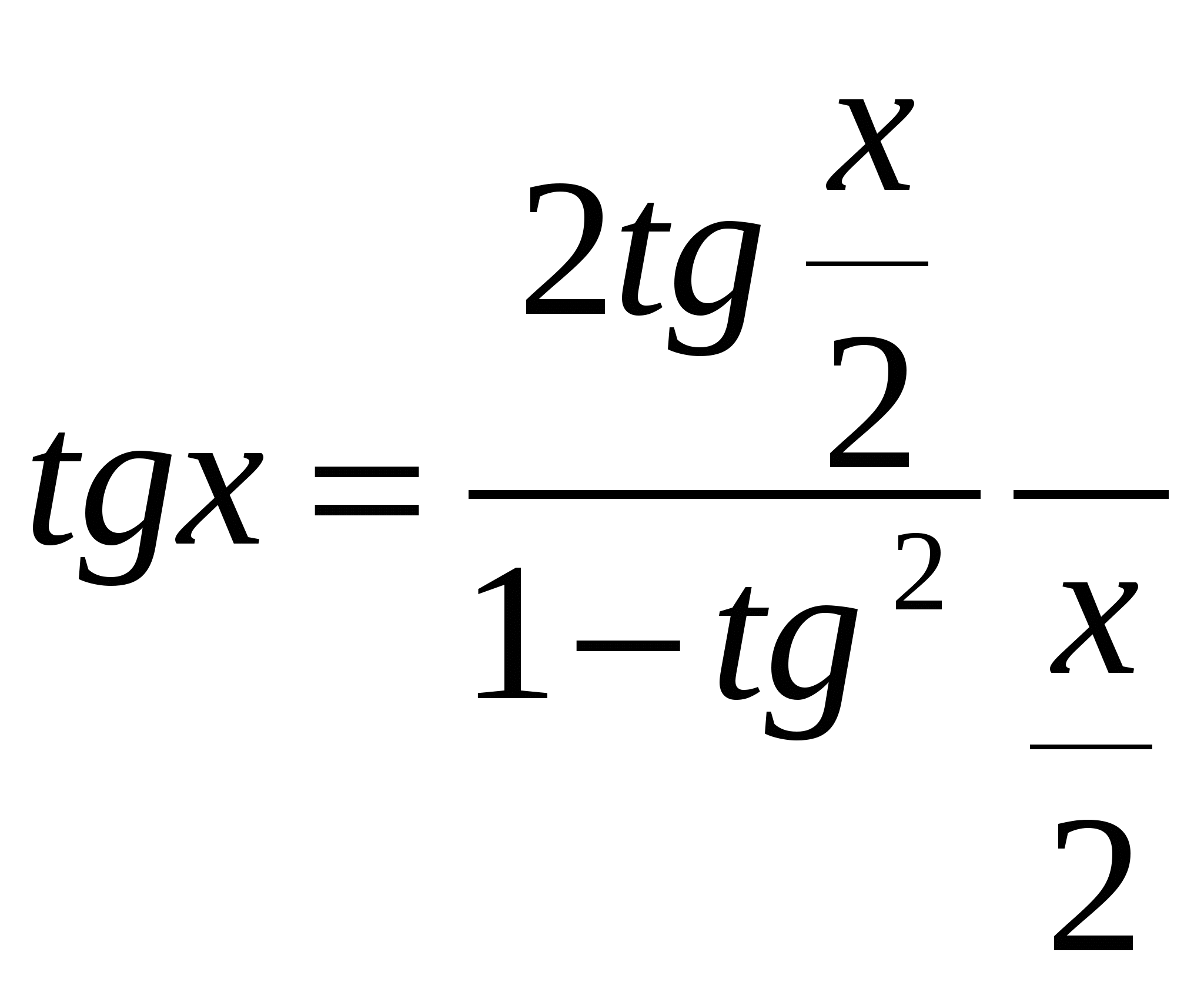но применение этой подстановки требует большой осторожности! Следует проверить, не является ли корнем данного уравнения ( иначе будет потеря корня). Это делается путем подстановки данной серии корней в первоначальное уравнение.

Подставим и убедимся, что это корень уравнения

,

0-1= -1,

- 1= -1(верно).

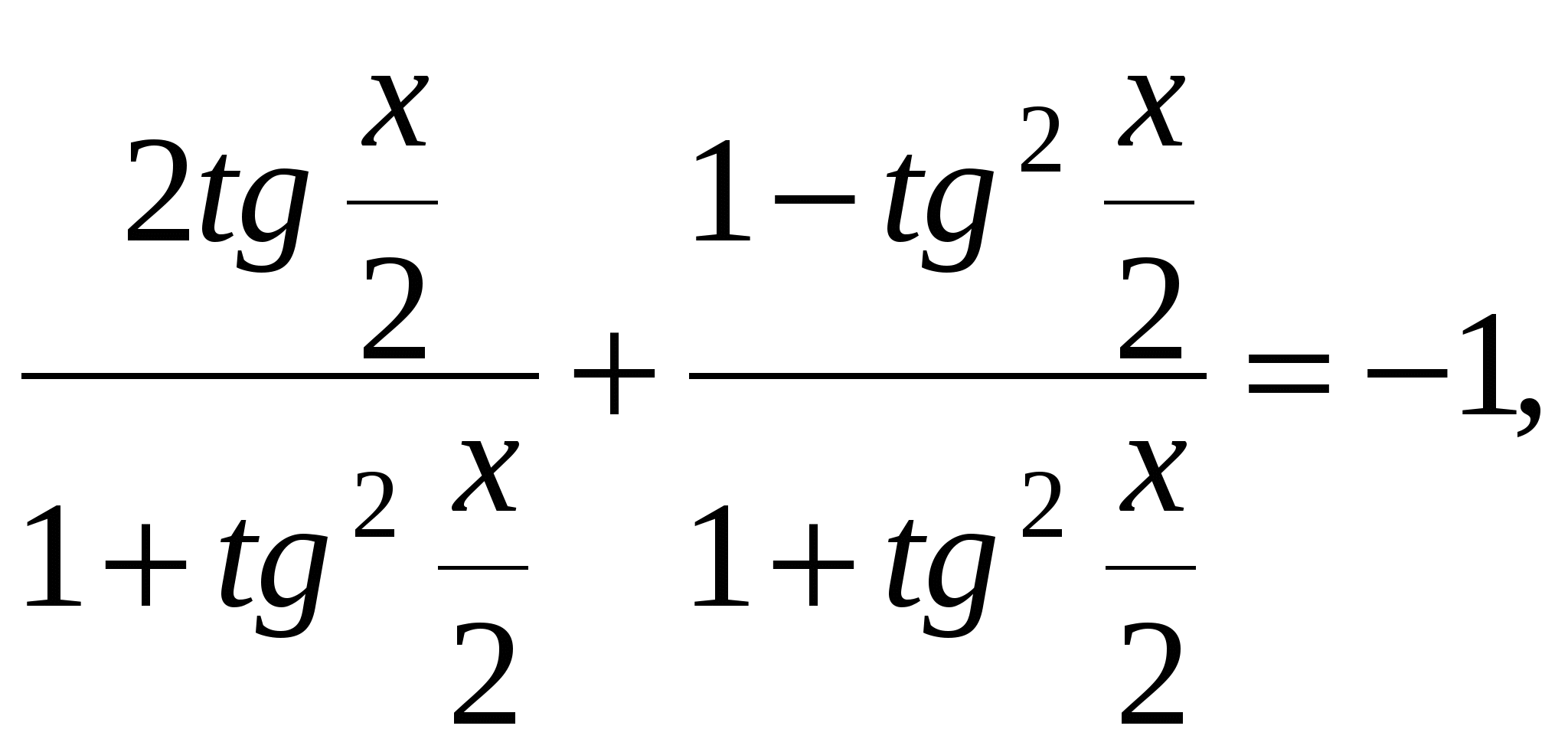пусть

2 способ решения этого уравнения:

sinx+cosx= -1,

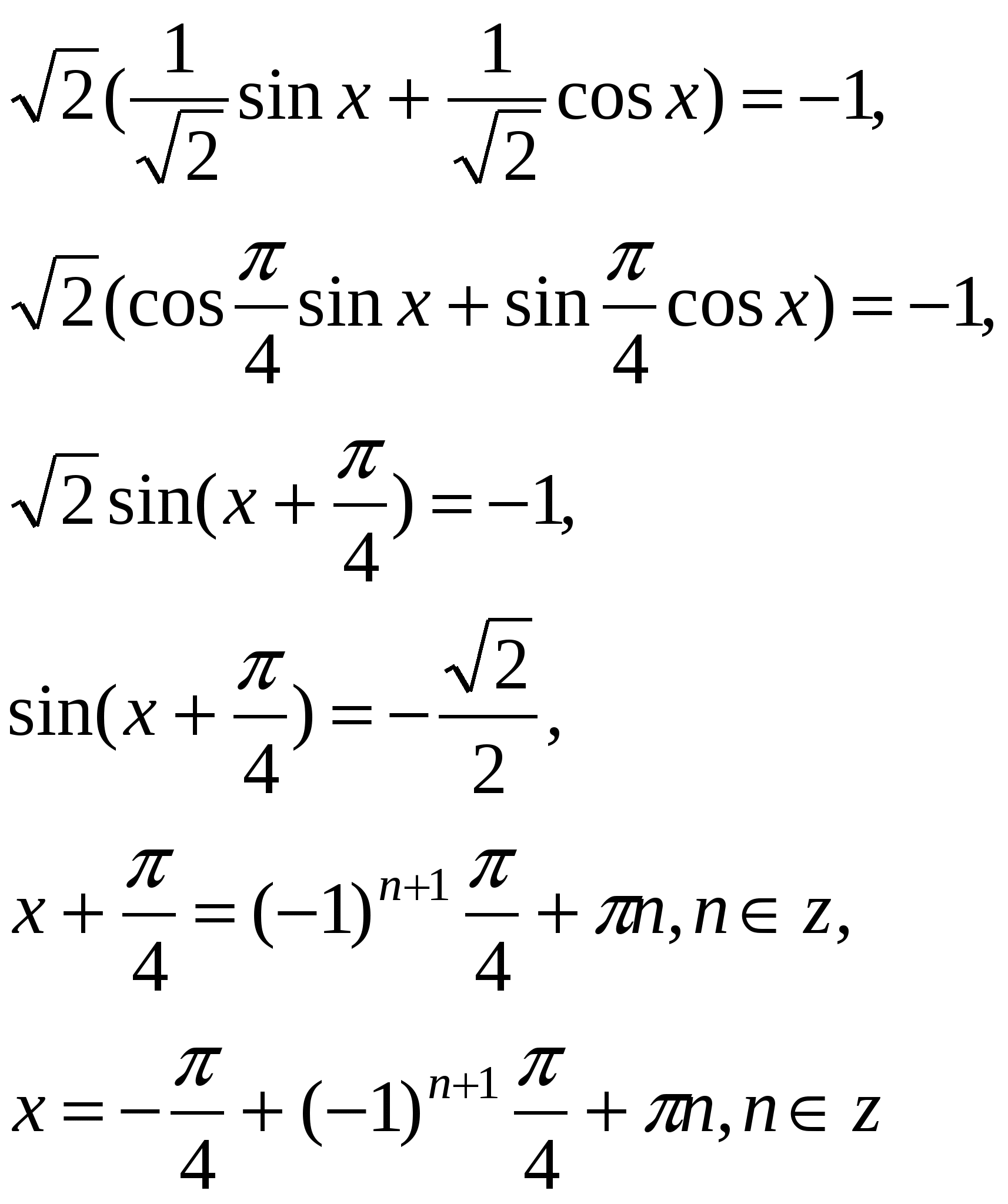
если

если

Ответ: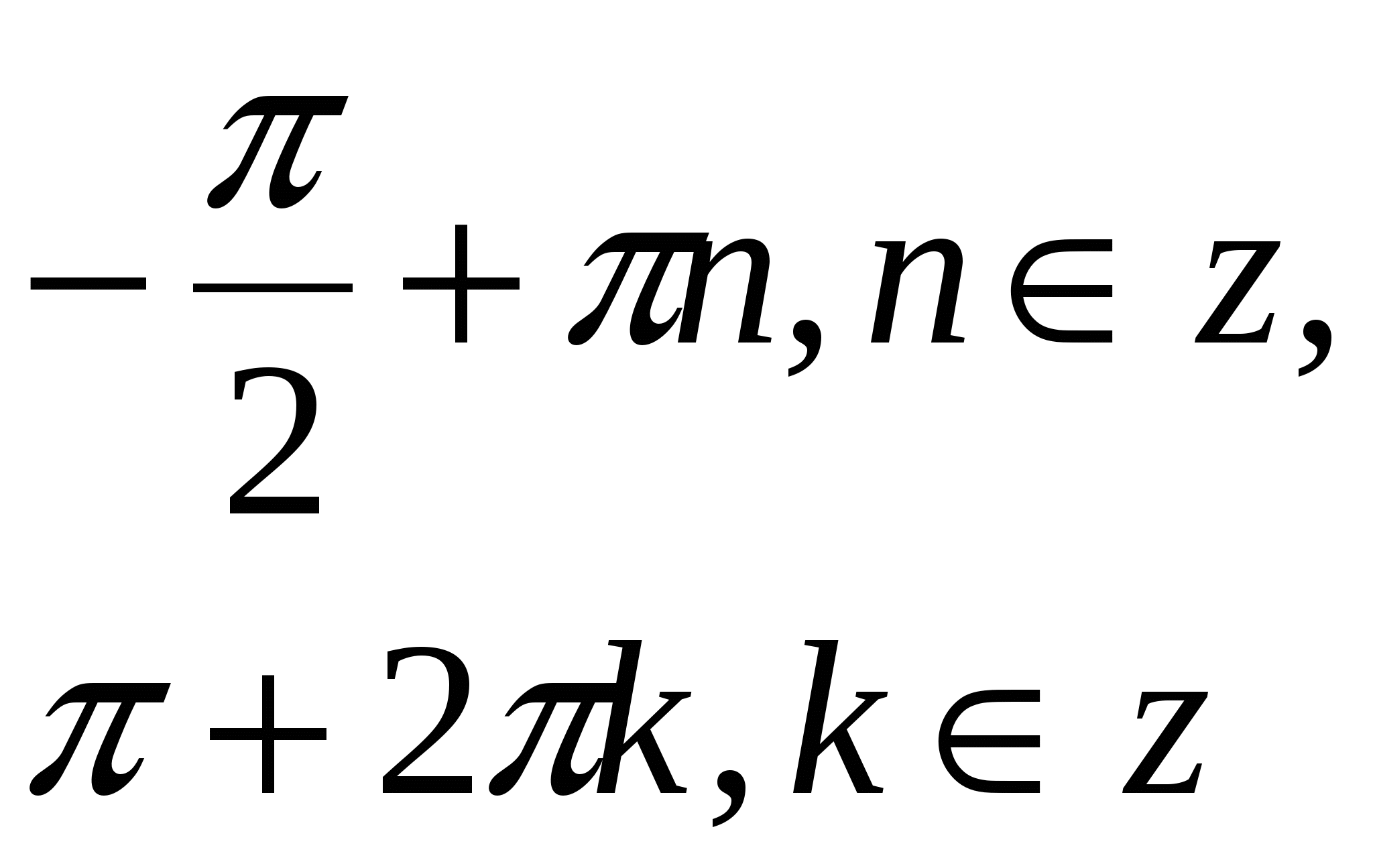

8.   Уравнения, решающие оценкой значений левой и правой частей:

а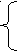)   2sin3x+4cosx=7

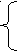
Следовательно:

Мы доказали, что данная сумма не должна превосходить 6, а по условию она равна 7, значит уравнение не имеет решения.

б)   3cos3x+cosx=4,

,

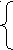то равенство возможно, если имеет решение система:

,

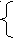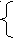
подставим во второе уравнений значение переменной первого уравнения:

, получили верное равенство, следовательно , является решением системы уравнений.

Ответ:

9. Комбинированные уравнения из заданий ЕГЭ

Чаще всего при решении уравнения используется несколько способов, например С1 из ЕГЭ 2002г.

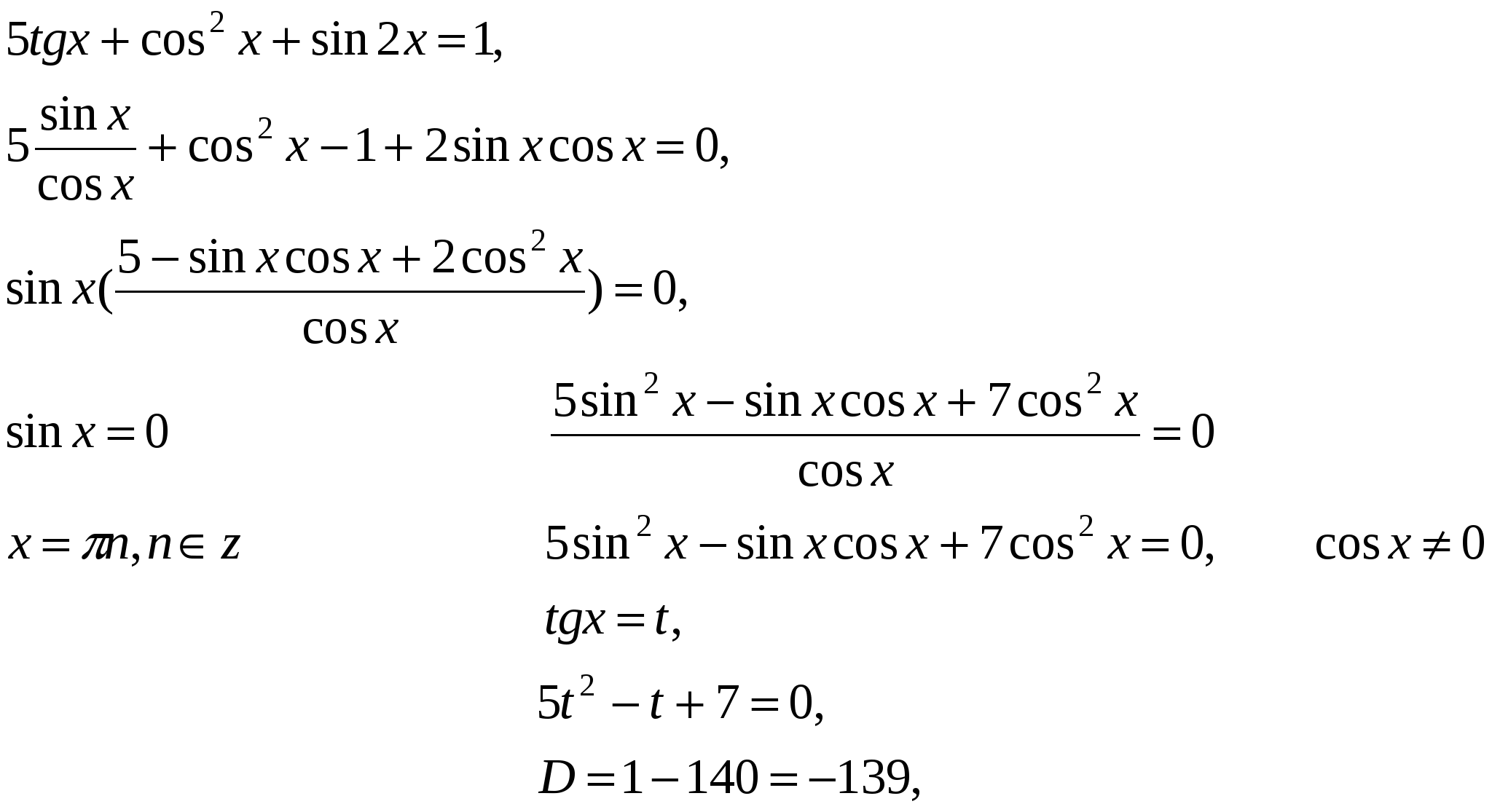
D<0, решений нет.

Ответ: .

Домашнее задание:

Задание В3 из ЕГЭ 2003:

Найти сколько корней имеет уравнение:

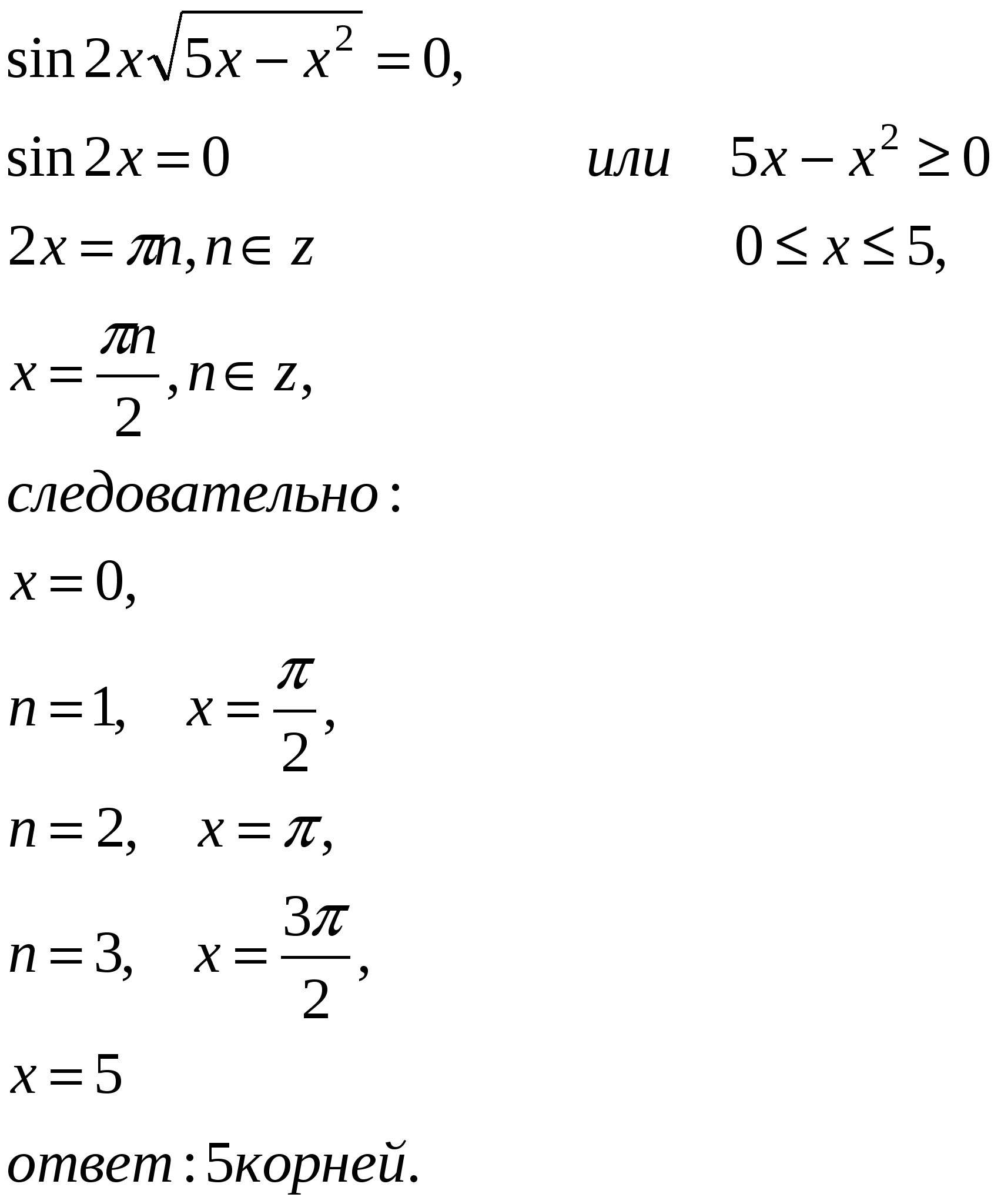
Домашнее задание:

Решить уравнение: ЕГЭ-2006:

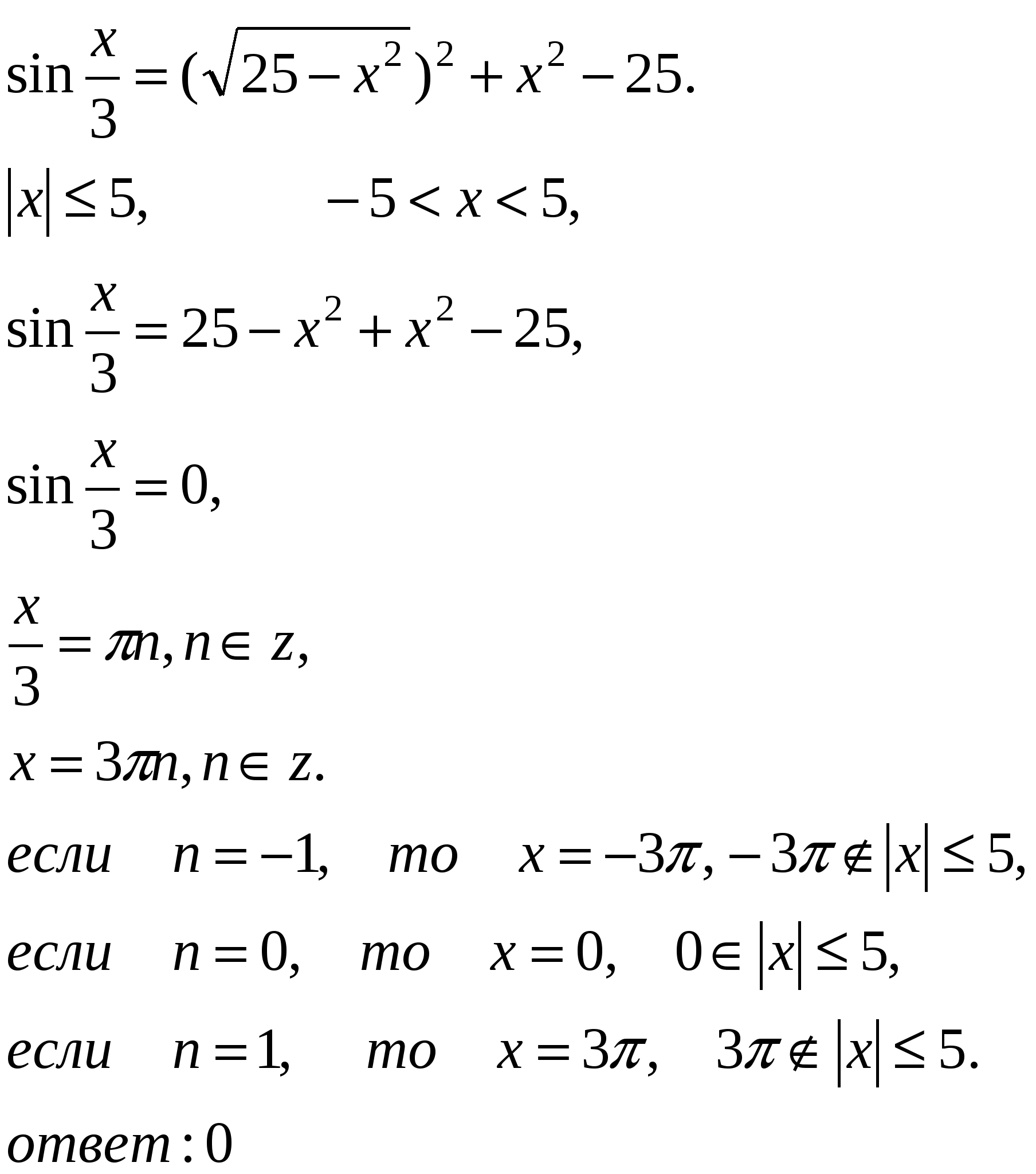
Домашнее задание:

Задание С2 из демоверсии 2007 года:

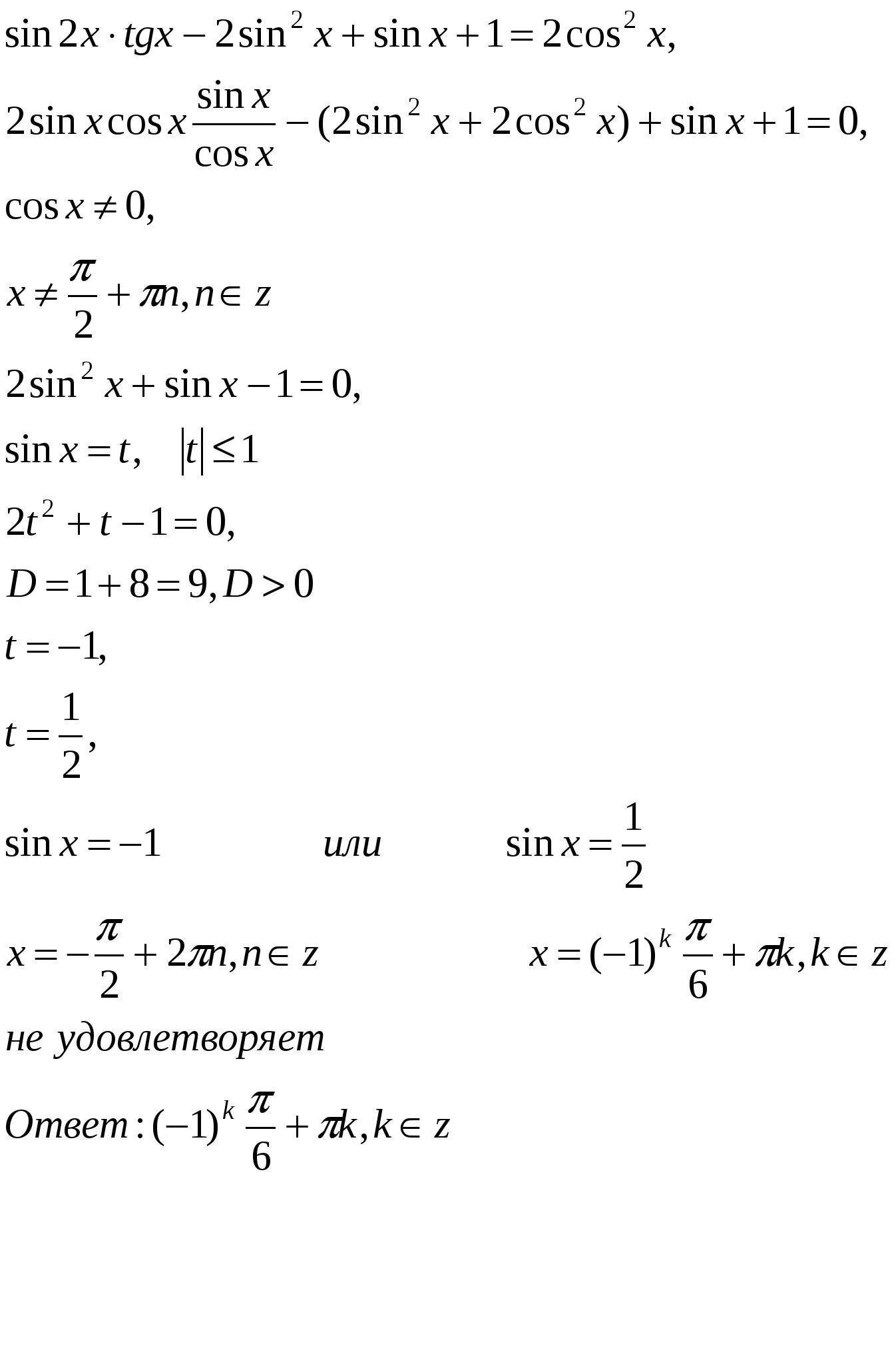
Домашнее задание:

Итог урока

Сегодня на уроке мы повторили и разобрали различные способы решения тригонометрических уравнений.

Домашнее задание было выдано в течение урока, а так же вам необходимо подготовиться к контрольному тесту по данной теме, который будете сдавать на компьютерах.

Каждый отвечающий получил оценку.

Урок №6: Контрольное тестирование по теме, с использованием компьютерной программы.

Тест по теме «Тригонометрические уравнения». Для запуска программы выполните следующие действия:

1. На диске CD-ROM открыть папку «ТРИГОНОМ_УРАВНЕНИЯ»

2. Запустить программу trigon.exe

3. В появившемся окне выбрать нужный вариант.

4. Решить предложенное уравнение и выбрать вариант ответа. Нажав на кнопку соответствующую варианту ответа, произойдет переход к следующему заданию. Всего заданий для каждого варианта семь.

5. После выполнения всех заданий компьютерная программа выдаст результат на экран. Программа ставит следующие оценки:

«ОТЛИЧНО» – при всех правильных ответах;

«ХОРОШО» – при одном неверном ответе;

«УДОВЛЕТВОРИТЕЛЬНО» – при двух неверных ответах;

«НЕУДОВЛЕТВОРИТЕЛЬНО» – при трех и более неверных ответах;

6. Для выхода из программы нажмите кнопку «Выход».