АЛГЕБРА И НАЧАЛА АНАЛИЗА.

Тема урока. «Чётность и нечётность функций. Нулевые функции».

Цели урока.

Образовательные: повторить основные теоретические понятия: четность и нечётность функций, свойство графика четной и нечётной функции, четность и нечетность тригонометрических функций. Изучить понятие нулевой функции, свойство графика нулевой функции, построить алгоритм исследования функции на четность и нечетность, сформировать умение променять его при решении примеров.

Развивающие: формирование умения наблюдать, проводить рассуждения по аналогии, обобщать, развивать логическое и творческое мышление.

Воспитательные: совершенствовать навыки коллективной работы, развивать умение анализировать ситуацию, выделять главное, сопоставлять факты. Развивать ассоциативное мышление.

Оборудование: компьютер, интерактивная доска, карточки для работы по группам, индивидуальные карточки для самостоятельной работы.

Ход урока.

1. Орг. момент. (Психологический настрой на урок).

2. Проверка домашнего задания.

1.Опрос теории.

1. Дать определение чётной функции.

Функция f(x) называется чётной, если она обладает двумя свойствами:

• её область определения симметрична относительно нуля;

• для любого х из области определения выполняется равенство: f(-x) = f (x).

1. Дать определение нечётной функции.

Функция f(x) называется нечётной, если она обладает двумя свойствами:

• её область определения симметрична относительно нуля;

- для любого х из области определения выполняется равенство: f(-x) = - f (x).

3. Сформулировать свойства графика чётной функции.

График чётной функции симметричен относительно оси ординат.

4. Сформулировать свойства графика нечётной функции.

График нечётной функции симметричен относительно начала координат.

5. Что вы можете сказать о чётности и нечётности тригонометрических функций.

Функции y = sin x, y = tg x, y = ctg x являются нечётными;

функция y = cos x является чётной.

2. Каждой группе было дано домашнее задание: исследовать функции на чётность и нечётность. По одному представителю от каждой группы выходят к доске.

I группа

f(x) = cos4x + 4cos2x –

+3

Решение:

f(-x) = cos(-4x) + 4cos(-2x) –= cos4x +4cos2x – + 3 = f(x);

f(x) – чётная функция.

II группа

g(x) = sinx·cos3x·cos4x – 0,25·(sin8x – sin6x + sin2x).

Решение:

g(-x) = sin (-x)·cos(-3x)·cos(-4x) – 0,25(sin(-8x) – sin(-6x) + sin(-2x)) = - sinxcos3xcos4x + 0,25(sin8x-sin6x+sin2x)= - g(x).

g(x) – нечётная функция.

III группа

h(x) = 1 + g(x)

Решение:

h(-x) = 1 + g(-x) = 1 – g(x).

Функция h(x) не является ни чётной, ни нечётной функцией.

2. Устно. ( Графики отображаются на экране).

1.Какая из указанных функций является:

1) нечетной; 2) четной; 3) не является ни четной ни нечетной?

3)

1)

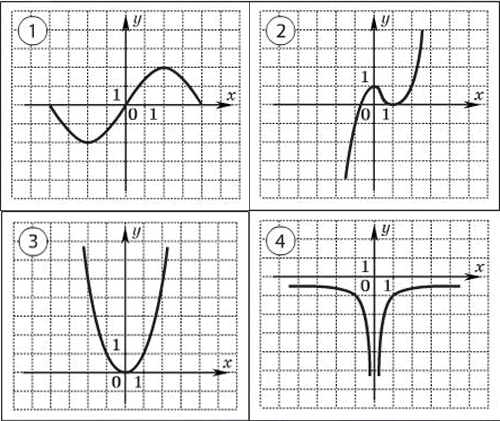
2)

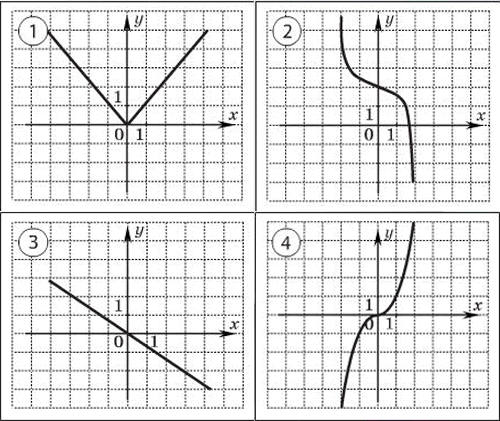
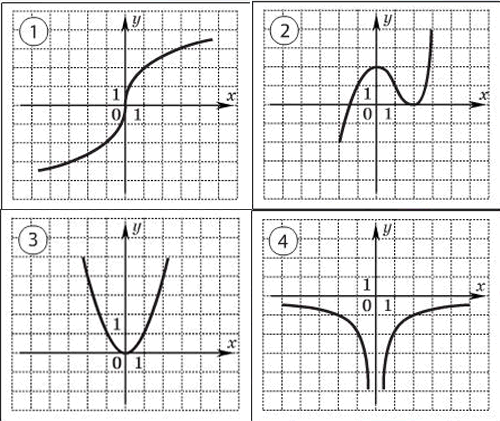
2.Определить, какие из указанных функций являются чётными и нечётными:

1); (область определения все числа и f(-x) = - f (x),нечетная).

Как можно изменить функцию f(х), что бы она стала ни четной ни нечётной?

-Можно прибавить число.

- Можно степень заменить на четную.

- Можно синус заменить на косинус.

2); (область определения все числа и f(-x) = f (x),четная).

Если к функции прибавить или отнять число, как это повлияет на четность?

-Функция останется четной.

3) h(х) = 5. (область определения все числа, четная).

( После устного счета отвечают те учащиеся, кто работал у доски).

3. Изучение новой темы.

Каждой группе было предложено задание на дом, упростить данные выражения. На уроке информатики Андрей Владимирович помог ребятам оформить решение каждого примера на компьютере в виде презентации.

I группа

f(x) = cos4x + 4cos2x –

- + 3 = 2cos²2x – 1 + +4cos2x+3 – =

II группа

g(x) = sinxcos3xcos4x – 0,25(sin8x – sin6x+ sin2x) = 0,5(sin4x – sin2x)cos4x –

- 0,25(sin8x – sin6x + sin2x) =

= 0,25sin8x – 0,5sin2xcos4x -

- 0,25(sin8x - sin6x + sin2x) = 0,25sin8x – 0,25(sin6x – sin2x) –

- 0,25(sin8x – sin6x + sin2x) = 0.

III группа

h(x) = 1.

-Ребята, мы видим, что, в третьем случае после преобразования выражения, задающего функцию h(х), мы получили h(х) = 1. Изобразите на доске график этой функции.

Из третьей группы ученик рисует на доске график функции h(х) = 1.

(На доске изображена заготовка прямоугольной системы координат).

y

h(x) = 1

0 х

Какой же является данная функция?

-Данная функция является четной.

- Вернемся к примерам 1-ой и 2-ой группы. Мы получили функции, области значения которых включают только 0. Такие функции называются нулевыми функциями

(На доске дописывается тема урока: «Нулевые функции»)

- Ребята, кто из вас ещё раз сформулирует определение нулевой функции.

Функция, область значения которой равна нулю, называется нулевой функцией.

- Как вы считаете, что будет являться графиком нулевой функции?

Графиком нулевой функции является ось абсцисс.

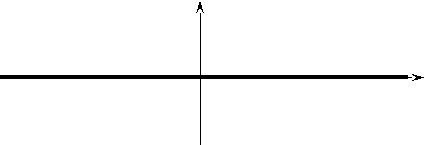
0 x

(Учащиеся пишут определение и строят график в тетрадь, одновременно определение и график функции отображается на экране).

- Как вы считаете, относительно чего симметрична данная прямая?

Прямая y = 0 симметрична как относительно оси ординат, так и относительно начала координат.

- Если графики нулевых функции f и g симметричны относительно начала координат, то функции f и g являются какими?

- Функции f и g являются нечетными.

- Если графики функций f и g симметричны относительно оси ординат, то функции f и g являются какими?

- Функции f и g являются четными.

- Какой можно сделать вывод на основании этих двух утверждений?

На основании этих утверждений заключаем, что функции f и g являются и чётными, и нечётными.

- Итак, функции f и g – нулевые и они являются и чётными и нечётными. Вместе с тем, возникает вопрос, а могут ли функции, являющиеся и чётными и нечётными, быть отличными от нулевых?

Чтобы ответить на этот вопрос, докажем утверждение: «Только нулевые функции могут быть и чётными, и нечётными».

Доказательство:

Если функция f является и чётной, и нечётной, то для любого выполняются оба равенства: f(-x) = f(x) и f(-x) = - f(x). Отсюда следует, что f(x) = - f(x), откуда 2f(x) = 0 и, наконец, f(x) = 0.

(Данное утверждение и доказательство отображается на экране, учащиеся записывают их в тетрадь).

-Отсюда делаем вывод: только нулевые функции могут быть и чётными, и нечётными.

IV. Закрепление.

1.Учащиеся работают по группам (Каждая группа получает карточку).

I группа. Исследовать на чётность и нечётность функцию и построить её график.

Решение: Область определения этой функции составляют все числа, кроме 0. А при х ≠ 0 имеем: Значит, данная функция является нулевой. Построим график этой функции. По графику видно, что она является и чётной, и нечётной. Кроме того, данная нулевая функция является разрывной.

0 x

II группа.

Исследовать на чётность и нечётность функцию и построить её график.

Решение:

Область определения этой функции составляют все числа, кроме х = 1. А при х ≠ 1 имеем: Следовательно, данная функция является нулевой. Её график представлен на рисунке.

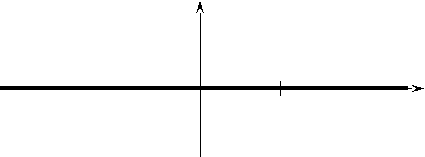y

0 1 x

Область определения данной функции есть множество, несимметричное относительно начала координат. Значит, данная функция, являясь нулевой, не является ни чётной, ни нечётной.

- Нулевых функций, которые задаются формулами, где , существует бесконечное множество, т. е. существует бесконечное множество функций, которые являясь нулевыми, не являются и четными и нечетными.

III группа.

Исследовать на чётность и нечётность функцию и построить её график.

Решение:

Область определения этой функции составляют все значения х, кроме х = 2, -2. А при х ≠ 2, -2 имеем: Следовательно, данная функция является нулевой. Её график представлен на рисунке.

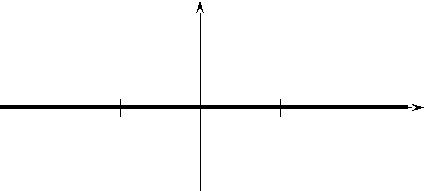y

-2 0 2 x

Область определения данной функции есть множество, симметричное относительно начала координат и данная функция является нулевой. Значит она является и чётной, и нечётной.

2. При решении задач на определение четности и нечетности функций удобно пользоваться следующим алгоритмом.

Алгоритм исследования функции на чётность и нечётность.

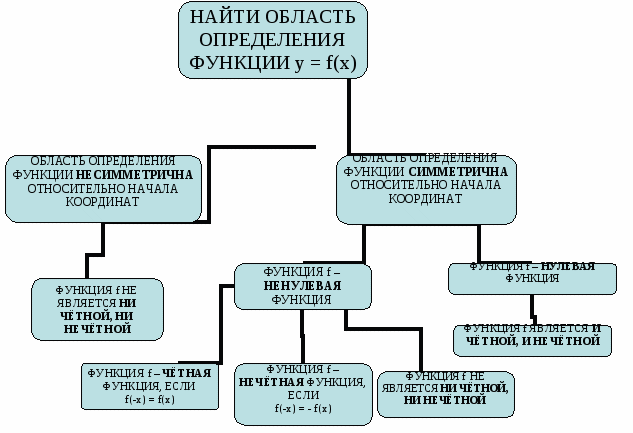
3. Самостоятельная работа по карточкам.

(Каждый учащийся группы получает карточку с заданиями).

Вариант 1.

1. Выяснить чётность и нечётность функции.

а); б).

2. Определить по графику чётность и нечётность функции.

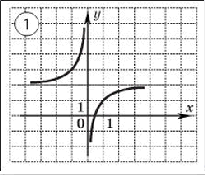
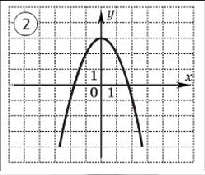
3. Исследовать функцию на чётность и нечётность и построить её график.

.

Вариант 2.

1. Выяснить чётность и нечётность функции.

а); б).

2. Определить по графику чётность и нечётность функции.

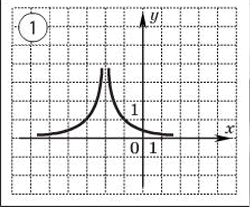
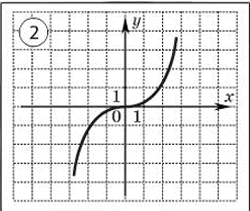
3. Исследовать функцию на чётность и нечётность и построить её график.

.

(Самопроверка).

V. Итог урока. Домашнее задание.

Учитель математики Виноградова Ольга Григорьевна, г.Новый Уренгой. 2012 г.