Рабочая программа по алгебре для 9 класса

Муниципальное образовательное учреждение средняя общеобразовательная школа №1 имени Героя Российской Федерации Ю.Д.Недвиги муниципального образования «Барышский район» Ульяновской области

Рабочая программа по алгебре для 9 класса

Подготовила учитель математики

Раиса Ивановна Исакова

УМК: Алгебра 8 Ю.Н. Макарычев, Н.Г. Миндюк и другие.

Пояснительная записка.

На алгебру в 9 классе в федеральном базисном плане отведено 3 часа в неделю за счет федерального компонента. Тематическое планирование составлено из расчета 102 часа в год.

Составлено планирование в соответствии с программой по алгебре для средней школы (5 – 9 классы), допущенной департаментом образовательных программ и стандартов общего образования министерства образования РФ. тематическое планирование составлено на основе Федерального Государственного стандарта, Примерной программы среднего (полного) общего образования по математике.

Изучение учебного предмета осуществляется на основании нормативно-правовых документов:

1. Закона «Об образовании» от 10.02.1992 года № 3266-1 (в ред. Федеральных законов от 13.01.1996 года № 12 – ФЗ с изменениями, внесёнными Постановлением Конституционного Суда РФ от 24.10.2000 года №13 – П и дополнениями, внесёнными Федеральными законами);

2. Приказа Минобразования Российской Федерации от 09.03.2004 года №1312 «Об утверждении Федерального базисного учебного плана и примерных учебных планов для общеобразовательных учреждений Российской Федерации, реализующих программы общего образования»;

3. Приказа Департамента образования от 20.06.2007 года № 415 «Об утверждении регионального базисного учебного плана и примерных учебных планов для общеобразовательных учреждений Ульяновской области, реализующих программы общего образования»;

4. САНПиН 2.4.2 № 1178-02, зарегистрированные в Минюсте России 05.12.2002 года, регистрационный № 3997;

5. Учебного плана МОУ СОШ №1 имени Ю. Д Недвиги МО «Барышский район» на 2010 – 2011 учебный год

6. Сборника нормативных документов. М.: Дрофа, 2004.- 174с.

ЦЕЛЬ:

УЧЕБНИК: Алгебра 9 2008 г

Ю.Н. Макарычев, Н.Г. Миндюк и другие.

Общая характеристика учебного предмета

Алгебра как содержательный компонент математического образования в основной школе нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.

Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.

При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.

В ходе освоения содержания курса учащиеся получают возможность:

развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Изучение математики на ступени основного общего образования направлено на достижение следующих целей:

овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Обязательный минимум содержания

Алгебраические выражения. Буквенные выражения (выражения с переменными). Допустимые значения переменных, входящих в алгебраические выражения. Числовое значение буквенного выражения.
Свойства степеней с целым показателем и их применение в преобразовании выражений. Многочлены. Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности. Формула разности квадратов, формулы суммы кубов и разности кубов. Разложение многочлена на множители. Вычисления значений арифметических и алгебраических выражений.
Квадратный трехчлен. Выделение полного квадрата в квадратном трехчлене. Разложение квадратного трехчлена на линейные множители. Многочлены с одной переменной. Степень многочлена. Корень многочлена. Алгебраические дроби. Действия с алгебраическими дробями. Преобразования алгебраических выражений.
Уравнения и неравенства. Уравнение с одним неизвестным. Корень уравнения. Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения, соотношения между коэффициентами и корнями. Решение рациональных уравнений. Примеры решения уравнений высших степеней; методы замены переменной, разложения на множители. Примеры уравнений с несколькими неизвестными. Система уравнений. Решение системы. Система двух линейных уравнений с двумя неизвестными. Методы подстановки и алгебраического сложения. Примеры решения нелинейных систем. Примеры решения уравнений в целых числах. Неравенство с одним неизвестным. Решение неравенства. Линейные неравенства с одним неизвестным и их системы. Квадратные неравенства. Примеры решения дробно-линейных неравенств. Примеры доказательств алгебраических неравенств. Составление уравнений, неравенств и их систем по условиям задач. Решение текстовых задач алгебраическим методом.

Координаты

Изображение чисел точками координатной прямой. Геометрический смысл модуля числа. Числовые промежутки: интервал, отрезок, полуинтервал, луч. Формула расстояния между точками координатной прямой.
Декартова система координат на плоскости. Координаты точки на плоскости. Уравнение прямой, уравнение окружности с центром в начале координат. Графическая интерпретация уравнений и неравенств с двумя неизвестными и их систем. Примеры графических зависимостей и функций, отражающих реальные процессы (в том числе периодические — синус; показательный рост).

Числовые функции

Понятие функции. Область определения функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции.
Прямая пропорциональность, линейная функция и ее график, геометрический смысл коэффициентов. Обратная пропорциональность и ее график (гипербола).
Квадратичная функция и ее график (парабола). Координаты вершины параболы, ось симметрии. Степенная функция с натуральным показателем и ее график.
Графики функций: корень квадратный, корень кубический, модуль.
Использование графиков функций для решения уравнений и систем.
Использование преобразований графиков (параллельный перенос вдоль осей координат и симметрия относительно осей).

Числовые последовательности и способы их задания

Арифметическая и геометрическая прогрессии. Формулы общего члена арифметической и геометрической прогрессий, суммы первых нескольких членов арифметической и геометрической прогрессий. Сложные проценты.

Элементы логики, комбинаторики, статистики и теории вероятностей

Множество. Элемент множества, подмножество. Объединение и пересечение множеств. Диаграммы Эйлера. Понятия об аксиомах и теоремах, следствиях, необходимых и достаточных условиях, контрпримерах, доказательстве от противного. Примеры решения комбинаторных задач: перебор вариантов, правило умножения. Представление данных в виде таблиц. диаграмм. графиков. Средние результаты измерений.
Понятие и примеры случайных событий. Частота событий, вероятность. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности.

Общеучебные умения, навыки и способы деятельности

В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

Результаты обучения

Результаты обучения задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние два компонента представлены отдельно по каждому из разделов содержания.

Требования к уровню подготовки выпускников

В результате изучения математики ученик должен

знать/понимать

существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

АЛГЕБРА

Уметь:

составлять буквенные выражения и формулы по условиям задач, осуществлять подстановку одного выражения в другое, осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одни переменные через другие;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для
вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы уравнений (линейные и системы, в которых одно уравнение второй, а другое первой степени);
решать линейные неравенства с одной переменной и их системы, квадратные неравенства;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, учитывать ограничения целочисленности, диапазона изменения величин;
определять значения тригонометрических выражений по заданным значениям углов;
находить значения тригонометрических функций по значению одной из них;
определять координаты точки в координатной плоскости, строить точки с заданными координатами; решать задачи на координатной плоскости: изображать различные соотношения между двумя переменными, находить координаты точек пересечения графиков;
применять графические представления при решении уравнений, систем, неравенств;
находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу;
строить графики изученных функций, описывать их свойства, определять свойства функции по ее графику; распознавать арифметические и геометрические прогрессии, использовать формулы общего члена и суммы нескольких первых членов.

Применять полученные знания:

для выполнения расчетов по формулам, понимая формулу как алгоритм вычисления; для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
при моделировании практических ситуаций и исследовании
построенных моделей (используя аппарат алгебры);
при интерпретации графиков зависимостей между величинами, переводя на язык функций и исследуя реальные зависимости; для расчетов, включающих простейшие тригонометрические формулы;
при решении планиметрических задач с использованием аппарата тригонометрии.

ЭЛЕМЕНТЫ ЛОГИКИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ

Уметь:

оценивать логическую правильность рассуждений, в своих доказательствах использовать только логически корректные действия, понимать смысл контрпримеров; извлекать информацию, представленную в таблицах, на диаграммах, на графиках; составлять таблицы; строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения; вычислять средние значения результатов измерений;
находить частоту события;
в простейших случаях находить вероятности случайных событий, в том числе с использованием комбинаторики.

Применять полученные знания:

при записи математических утверждений, доказательств, решении задач;
в анализе реальных числовых данных, представленных в виде диаграмм, графиков;
при решении учебных и практических задач, осуществляя
систематический перебор вариантов;
при сравнении шансов наступления случайных событий;
для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией

Уровни подготовки учащихся и критерии успешности обучения по математике

Уровни

Оценка

Теория

Практика

Узнавание

Алгоритмическая деятельность с подсказкой

«3»

Распознавать объект, находить нужную формулу, признак, свойство и т.д.

Уметь выполнять задания по образцу, на непосредственное применение формул, правил, инструкций и т.д.

Воспроизведение

Алгоритмическая деятельность без подсказки

«4»

Знать формулировки всех понятий, их свойства, признаки, формулы.

Уметь воспроизвести доказательства, выводы, устанавливать взаимосвязь, выбирать нужное для выполнения данного задания

Уметь работать с учебной и справочной литературой, выполнять задания, требующие несложных преобразований с применением изучаемого материала

Понимание

Деятельность при отсутствии явно выраженного алгоритма

«5»

Делать логические заключения, составлять алгоритм, модель несложных ситуаций

Уметь применять полученные знания в различных ситуациях. Выполнять задания комбинированного характера, содержащих несколько понятий.

Овладение умственной самостоятельностью

Творческая исследовательская деятельность

«5»

В совершенстве знать изученный материал, свободно ориентироваться в нем. Иметь знания из дополнительных источников. Владеть операциями логического мышления. Составлять модель любой ситуации.

Уметь применять знания в любой нестандартной ситуации. Самостоятельно выполнять творческие исследовательские задания. Выполнять функции консультанта.

Оценка письменных работ учащихся

Оценка «5» ставится, если:

- работа выполнена полностью;

- в логических рассуждениях и обоснованиях решения нет пробелов, ошибок;

- в решении нет математических ошибок ( возможна одна неточность, описка ).

Оценка «4» ставится, если:

- работа выполнена полностью, но обоснования шагов решения недостаточны;

- допущена одна ошибка, или есть два-три недочета в выкладках, рисунках, чертежах, графиках и т.д.

Оценка «3» ставится, если:

- допущено более одной ошибки или более двух-трех недочетов в выкладках, рисунках, чертежах, графиках, но учащийся обладает обязательными умениями по проверяемой теме.

Оценка «2» ставится, если:

- допущены существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.

Оценка «1» ставится, если:

- работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно;

- выполнено менее 1/3 части работы.

Тема: Квадратичная функция (20 часов)

Интегрирующая дидактическая цель

Обучающие и интеллектуально-развивающие цели обеспечивают усвоение темы на уровне:

Знания – ученик должен знать:

- употребляемые термины (функция, область определения функции, множество значений функции, нули, промежутки возрастания и убывания, квадратный трёхчлен, корни квадратного трёхчлена);

- определение функции, её свойств; определение квадратного трёхчлена и способ нахождения его корней, алгоритм разложения квадратного трёхчлена на множители;

- определение квадратичной функции, её свойства

- алгоритм исследования квадратичной функции;

- методы решения задач по теме «Квадратичная функция»

Понимания – ученик должен понимать:

-употребляемые термины;

- алгоритм исследования квадратичной функции.

Применения – ученик должен уметь:

- правильно употреблять функциональную символику и терминологию;

- по графику функции перечислять её свойства;

- находить дискриминант и корни квадратного трёхчлена, выделять квадрат трёхчлена, раскладывать его на множители;

- строить график квадратичной функции по алгоритму.

Ученик может:

- усвоить приёмы решения задач различной степени трудности

- научиться решать задачи по теме «Квадратичная функция» различными способами.

Обобщения и систематизации знаний – ученик имеет возможность:

- получить дополнительные исторические сведения;

- использовать приобретённые теоретические сведения для решения более сложных задач.

Воспитательные цели

Ученик:

- развивает навыки устной речи, умение грамотно вести диалог;

- развивает образное мышление;

- осознаёт необходимость самостоятельных действий при решении проблем;

- осознанно перерабатывает полученные знания для выработки целостной системы знаний по данной теме;

- развивает общие навыки учебной деятельности;

- строит собственные планы в соответствии с собственными способностями, интересами, убеждениями;

- проявляет интерес к сотрудничеству в групповой работе.

№ п\п

Тема учебного занятия

пункт

Дата

Ко- во часов

Тип учебного занятия, форма его проведения

Дидактические цели урока

Методы обуч,

Формы позн деят

Межпред связи, наглядн

контроль

Лит-ра, образоват продукт

Функция и её свойства. Область определения и множество значений

П 1

2 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать: определение функции и понятие области определения и множества значений, определение графика функции

Ученик должен уметь: правильно употреблять функциональную символику и терминологию; понимать её при чтении текста, в устной речи учителя и учеников; находить значения функции, заданной формулой, таблицей, графиком; решать обратную задачу; строить графики элементарных функций;

на уровне выше обязательного строить графики функций «Целая часть числа», «Дробная часть числа»

1) объяс-иллюст

Фронт

2) част- поиск

Фронт

Индив

Табл

«Св.функции»

Презент

«Функ

ции и графики»

Сам раб

№22/98 стр 3

Свойства функций

П 2

3 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

3) урок прим знан и умен

Ученик должен знать: основные свойства функций (нули, возрастание и убывание, промежутки постоянного знака); свойства функций

Ученик должен уметь: по графику функции перечислять её свойства, то есть указывать нули, промежутки монотонности, знакопостоянства; строить графики основных функций и работать с графиком любой функции

строить графики функций с модулем

1) объяс-иллюст

Фронт

2) репрод фронт индив

3) част- поиск

Фронт

Индив

физика

«графики изотермизобар

изохор процессов»

Сам раб

Квадратный трёхчлен

П 3

3 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать: определение квадратного трёхчлена, его корней; порядок нахождения корней квадратного трёхчлена, алгоритм выделения квадрата двучлена.

Ученик должен уметь: находить дискриминант и корни квадратного трёхчлена; определять наличие корней и их количество;

выделять квадрат двучлена из квадратного трёхчлена на примерах;

выделять квадрат двучлена в общем виде, решать задачи повышенного уровня сложности с параметрами.

1) объяс-иллюст

Фронт

2) част- поиск

Фронт

Индив

3) част- поиск

Фронт

Индив

Алгебра 8 «Квадратные уравнения»

Разложение квадратного трёхчлена на множители

п 4

2 часа

1) урок изучения нового мат.

2)урок прим знан и умен

Ученик должен знать: теоремы о разложении квадратного трёхчлена на множители; алгоритм разложения квадратного трёхчлена на множители. Ученик должен уметь: раскладывать квадратный трёхчлен на множители, использовать это разложение при доказательстве тождеств;

решать задания с дробями, используя разложение на множители;

применять разложение на множители в нестандартных задачах и задачах повышенной сложности.

1) объяс-иллюст

Фронт

2)част- поиск

Фронт

Индив

Функция и её график

п 5

2 часа

1) урок изучения нового мат.

2)урок прим знан и умен

Ученик должен знать определение функции и её свойства при различных значениях параметра a.

Ученик должен уметь: строить график функции ; находить по графику промежутки возрастания и убывания, знакопостоянства; определять принадлежность точки графику;

определять точки пересечения графиков функций;

решать задачи с параметрами и задачи повышенной сложности

1) объяс-иллюст

Фронт

2)част- поиск

Фронт

Индив

Графики функций

п 6

2 часа

1) урок изучения нового мат.

2)урок прим знан и умен

Ученик должен знать алгоритм построения графиков функций из графика функции .

Ученик должен уметь изображать схематически и с помощью шаблона параболы графики функций ,;

строить графики этих функций с помощью параллельного переноса;

решать задачи повышенного уровня сложности

1) объяс-иллюст

Фронт

2) част- поиск

Фронт

Индив

Таблица

Подгот. Шпарг

«Кв. функц»

Построение графика квадратичной функции

п 7

3 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

3) урок прим знан и умен

Ученик должен знать: алгоритм построения графика квадратичной функции; формулы координат вершины параболы; свойства квадратичной функции.

Ученик должен уметь: строить график квадратичной функции по алгоритму; указывать координаты вершины параболы; уравнение оси симметрии, направление «ветвей» параболы; находить по графику промежутки возрастания и убывания функции

1) объяс-иллюст

Фронт

2) част- поиск

Фронт

Индив

3) част- поиск

Фронт

Индив

Презент

«Гра

фик кв.фун»

Таблица

№20/01 стр 17

22/02

стр 11

№19/02 стр 18

Обобщающий урок по теме «Квадратичная функция»

1 час

Урок обобщения и систем знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Ученик должен уметь применять полученные знания при решении типовых задач и задач более сложных, требующих переноса знаний и умений

част- поиск

Фронт

Индив

През.

«Преобразов.графика кв.фун»

тест

Контрольная работа № 1 по теме «Квадратичная функция»

1 час

Урок контроля знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Метод письменного контроля

индивид

к/р

10.

Анализ контрольной работы

1 час

Урок коррекции знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Ученик должен уметь анализировать результаты своей деятельности, проводить работу над ошибками

част- поиск

Фронт

Индив

Тема: Степенная функция. Корень n –й степени из числа (7 часов)

Интегрирующая дидактическая цель

Обучающие и интеллектуально-развивающие цели обеспечивают усвоение темы на уровне:

Знания – ученик должен знать:

- употребляемые термины (чётная и нечётная функции, степенная функция, арифметический корень n – й степени из числа);

- формулировки теорем, свойств, следствий из них по данной теме;

- алгоритм решения задач обязательного уровня.

Понимания – ученик должен понимать:

- употребляемые термины, теоремы, формулы; алгоритм решения типовых задач.

Применения – ученик должен уметь:

- определять чётность и нечётность функции, пользоваться этими свойствами при построении графиков функций у=хⁿ, определять по графику чётность и нечётность функции;

- находить значение выражений, включающих в себя корень n – й степени из числа;

- применять определения, свойства, теоремы, формулы к решению задач обязательного уровня;

- решать простейшие задачи прикладного характера;

Ученик может:

- научиться решать задачи прикладного характера;

- научиться составлять творческие задания.

Обобщения и систематизации знаний – ученик имеет возможность:

- решать задачи более сложного характера

- использовать приобретённые теоретические сведения для решения более сложных задач.

- переносить знания в смежные дисциплины

Воспитательные цели

Ученик:

- развивает познавательные процессы, память, воображение, мышление, внимание, наблюдательность, сообразительность;

- вырабатывает критичность в выборе пути, критерии оценки своей работы и работы товарища;

- повышает интерес к решению нестандартных задач;

- формирует у себя положительный мотив учения.

№ п\п

Тема учебного занятия

пункт

Дата

Ко- во часов

Тип учебного занятия, форма его проведения

Дидактические цели урока

Методы обуч,

Формы позн деят

Межпред связи, наглядн

контроль

Лит-ра, образоват продукт

Степенная функция

П 21- 22

2 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать: определение чётной и нечётной функций, особенности графиков степенных функций при различных значениях n; алгоритм определения чётности и нечётности функций; свойства степенной функции;

аналитически доказывать свойства степенной функции.

Ученик должен уметь: определять чётность и нечётность функций, пользоваться этими свойствами при построении графика степенной функции, описывать её свойства;

определять по графику чётность и нечётность функции; аналитически доказывать свойства степенной функции;

строить графики с помощью симметрии, строить графики сложного вида.

1) объяс-иллюст

Фронт

индивид

2)част- поиск

Фронт

Индив

№5/01

Корень n- степени. Свойства корня n- й степени

П 23-24

2 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать: определение корня n-й степени из числа, арифметического корня n-й степени из числа; графическое и аналитическое решение уравнения вида х²=а; свойства арифметического корня n-й степени из числа, корень их произведения, дроби, основное свойство корня.

Ученик должен уметь: находить значение корня n-й степени из числа, значение корня по графику степенной функции; решать уравнения (двучленные и высших степеней) графически и аналитически; находить значение выражений, включающих в себя корень n-й степени из числа;

доказывать свойства арифметического корня n-й степени из числа

1) объяс-иллюст

Фронт

индивид

2)част- поиск

Фронт

Индив

Сам раб

№10/

2000

№36/01 стр 38

Обобщающий урок по теме «Степенная функция. Корень n-й степени из числа»

1 час

Урок обобщения и систем знаний и умений

Ученик должен знать вопросы теории по изученной теме.

част- поиск

Фронт

Индив

тест

Контрольная работа № 1 по теме «Степенная функция. Корень n-й степени из числа»

1 час

Урок контроля знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Метод письменного контроля

индивид

к/р

Анализ контрольной работы

1 час

Урок коррекции знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Ученик должен уметь анализировать результаты своей деятельности, проводить работу над ошибками

част- поиск

Фронт

Индив

Тема: Уравнения и неравенства с одной переменной. (18 часов)

Интегрирующая дидактическая цель

Обучающие и интеллектуально-развивающие цели обеспечивают усвоение темы на уровне:

Знания – ученик должен знать:

- употребляемые термины (уравнение, корни уравнения, системы уравнений, решения системы уравнений);

- определение целого уравнения, способы решения целого уравнения;

- графический способ решения систем уравнений;

- алгоритм решения систем уравнений, задач с помощью систем уравнений

Понимания – ученик должен понимать:

- алгоритм решения систем уравнений и алгоритм решения задач с помощью систем.

Применения – ученик должен уметь:

- решать целые уравнения, системы уравнений и задачи с помощью систем уравнений

Ученик может:

- научиться решать целые уравнения и системы уравнений различными способами;

- научиться решать задачи различными способами;

- ознакомиться с историей возникновения уравнений и поисками их решений;

Обобщения и систематизации знаний – ученик имеет возможность:

- использовать приобретённые теоретические сведения для решения более сложных задач.

Воспитательные цели

Ученик:

- выполняет заданную учителем работу;

- подчиняется правилам поведения;

- участвует в обсуждении вопросов;

-проявляет интерес к учебному предмету;

- строит собственные планы в соответствии с собственными интересами и убеждениями;

- рационально организовывает свой труд;

- сознательно относится к учебному труду;

- развивает творческие способности, самостоятельность.

№ п\п

Тема учебного занятия

пункт

Дата

Ко- во часов

Тип учебного занятия, форма его проведения

Дидактические цели урока

Методы обуч,

Формы позн деят

Межпред связи, наглядн

контроль

Лит-ра, образоват продукт

Целое уравнение и его корни

П 10

1 час

урок изучения нового мат.

Ученик должен знать: определение целого уравнения, его степени, способы решения целых уравнений.

Ученик должен уметь: находить степень целого уравнения, определять количество корней, решать целое уравнение с помощью разложения на множители путём простейших преобразований;

решать целое уравнение графически, доказывать существование корней;

решать уравнения с помощью теоремы Безу, решать уравнения с модулем.

объяс-иллюст

Фронт

Сам раб

№27-28/ 2002 стр 39

Уравнения, приводимые к квадратным

П 12

2 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать определение биквадратного уравнения и уравнений высших степеней методом введения новой переменной.

Ученик должен уметь: решать простейшие биквадратные уравнения методом ведения нолвой переменной;

решать усложнённые квадратные уравнения, уравнения высших степеней разложением на множители;

решать задачи повышенного уровня сложности

1) объяс-иллюст

Фронт

2) част- поиск

Фронт

Индив

Сам раб

№10/

2000

№36/01 стр 38

Дробные рациональные уравнения

4 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

3) урок прим знан и умен

4) комб урок

Ученик должен знать, какое уравнение называется рациональным, целым, дробным; алгоритм решения дробных рациональных уравнений и алгоритм решения текстовых задач с помощью рациональных выражений.

Ученик должен отличать по записи дробные рациональные уравнения, приводить примеры целого и дробного рационального уравнения, решать дробные рациональные уравнения различной степени трудности, применяя соответствующий алгоритм и решать текстовые задачи различной степени трудности с помощью рациональных уравнений

1) объяс-иллюст

Фронт

2) репрод фронт индив

3) част- поиск

Фронт

Индив34) част- поиск

Фронт

Индив

Решение неравенств второй степени с одной переменной

п 8

3 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

3) урок прим знан и умен

Ученик должен знать алгоритм решения квадратного неравенства с одной переменной (с использованием свойств квадратичной функции).

Ученик должен уметь решать неравенства вида

, где а не равно 0, применяя основные свойства квадратичной функции;

решать более сложные неравенства, в том числе дробно-рациональные, сводящиеся к квадратным неравенствам второй степени с одной переменной;

решать задачи с помощью неравенств, решать неравенства повышенной сложности.

1) объяс-иллюст

Фронт

2) част- поиск

Фронт

Индив

3) част- поиск

Фронт

Индив

Таблица

Метод интервалов

п 9

2 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать алгоритм решения неравенств методом интервалов.

Ученик должен уметь простейшие неравенства вида ;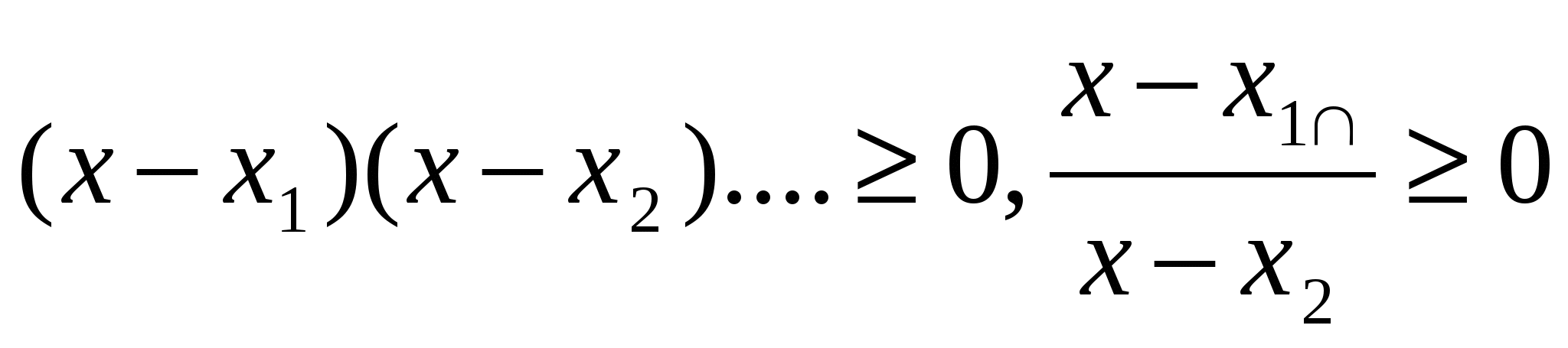

решать более сложные неравенства, в том числе и дробно-рациональные, находить область определения функции;

решать задачи повышенного уровня сложности.

1) объяс-иллюст

Фронт

2) част- поиск

Фронт

Индив

Обобщающий урок по теме «Уравнения и неравенства с одной переменной

1 час

Урок обобщения и систем знаний и умений

Ученик должен знать вопросы теории по изученной теме.

част- поиск

Фронт

Индив

тест

Контрольная работа № 1 по теме «Уравнения и неравенства с одной переменной»

1 час

Урок контроля знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Метод письменного контроля

индивид

к/р

Анализ контрольной работы

1 час

Урок коррекции знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Ученик должен уметь анализировать результаты своей деятельности, проводить работу над ошибками

част- поиск

Фронт

Индив

Тема: Уравнения и неравенства с двумя переменными и их системы (20 часов)

Интегрирующая дидактическая цель

Обучающие и интеллектуально-развивающие цели обеспечивают усвоение темы на уровне:

Знания – ученик должен знать:

- употребляемые термины (уравнение, корни уравнения, неравенства, решения неравенства);

- определение уравнения и неравенства с двумя переменными и его график;

- графический способ решения систем уравнений и неравенств с двумя переменными;

- алгоритм решения систем уравнений и неравенств, задач с помощью систем уравнений и неравенств:

Понимания – ученик должен понимать:

- алгоритм решения систем уравнений и неравенств, алгоритм решения задач с помощью систем.

Применения – ученик должен уметь:

- системы уравнений и неравенств, задачи с помощью систем уравнений и неравенств;

Ученик может:

- научиться решать системы уравнений различными способами;

- научиться решать задачи различными способами;

- ознакомиться с историей возникновения уравнений и неравенств, поисками их решений;

Обобщения и систематизации знаний – ученик имеет возможность:

- использовать приобретённые теоретические сведения для решения более сложных задач.

Воспитательные цели

Ученик:

- выполняет заданную учителем работу;

- подчиняется правилам поведения;

- участвует в обсуждении вопросов;

-проявляет интерес к учебному предмету;

- строит собственные планы в соответствии с собственными интересами и убеждениями;

- рационально организовывает свой труд;

- сознательно относится к учебному труду;

- развивает творческие способности, самостоятельность.

№ п\п

Тема учебного занятия

пункт

Дата

Ко- во часов

Тип учебного занятия, форма его проведения

Дидактические цели урока

Методы обуч,

Формы позн деят

Межпред связи, наглядн

контроль

Лит-ра, образоват продукт

Уравнения с двумя переменными и их системы.

2 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

Графический способ решения систем уравнений

П 12

4 часа

1) урок изучения нового мат.

2) урок закр знаний и ум

Ученик должен знать графический способ решения систем уравнений с двумя переменными.

Ученик должен уметь: решать графически системы уравнений с двумя переменными, используя простейшие графики;

решать более сложные уравнения, находить количество решений системы уравнений.

1) объяс-иллюст

Фронт

индивид

2)част- поиск

Фронт

Индив

Таблица

Решение систем уравнений второй степени

п 13

4 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

3) урок прим знан и умен

Ученик должен знать способы решения и алгоритмы каждого способа решения систем уравнений второй степени.

Ученик должен уметь: решать системы уравнений с двумя переменными, где одно из уравнений первой степени, а другое второй, методом подстановки;

решать боле сложные системы уравнений способом подстановки, сложения аналитически и графически;

выполнять задания на доказательство равносильности систем, где оба уравнения второй степени.

1) объяс-иллюст

Фронт

2) част- поиск

Фронт

Индив

3) част- поиск

Фронт

Индив

Таблица

Решение задач с помощью систем уравнений

п 14

2 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

3) урок прим знан и умен

Ученик должен знать алгоритм решения задач с помощью систем уравнений второй степени.

Ученик должен уметь: решать задачи с простейшими условиями с помощью систем уравнений;

решать задачи на движение, на совместную работу;

решать задачи повышенной сложности с практическим содержанием

1) объяс-иллюст

Фронт

индивид

2)част- поиск

Фронт

Индив

№34, 37, 38/01 №23/02 стр10 №27-28/02 стр 35

Неравенства с двумя переменными

2 часа

1) урок изучения нового мат.

2) урок закр знаний и ум

Ученик должен знать, что называется неравенства с двумя переменными, как изображается на координатной плоскости множество решений неравенства с двумя переменными, какая пара чисел является решением.

Ученик должен уметь изображать на координатной плоскости множество решений неравенства с двумя переменными, определять является ли пара чисел решением неравенства

1) объяс-иллюст

Фронт

индивид

2)част- поиск

Фронт

Индив

Системы неравенств с двумя переменными

2 часа

1) урок изучения нового мат.

2) урок закр знаний и ум

Ученик должен знать, что называется системой неравенств с двумя переменными, как изображается на координатной плоскости множество решений системы неравенств с двумя переменными, какая пара чисел является решением.

Ученик должен уметь изображать на координатной плоскости множество решений системы неравенств с двумя переменными, определять является ли пара чисел решением системы неравенства

1) объяс-иллюст

Фронт

индивид

2)част- поиск

Фронт

Индив

Обобщающий урок по теме «Уравнения и неравенства с двумя

1 час

Урок обобщения и систем знаний и умений

Ученик должен знать вопросы теории по изученной теме.

част- поиск

Фронт

Индив

тест

Контрольная работа № 1 по теме «Уравнения и неравенства с двумя переменными»

1 час

Урок контроля знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Метод письменного контроля

индивид

к/р

Анализ контрольной работы

1 час

Урок коррекции знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Ученик должен уметь анализировать результаты своей деятельности, проводить работу над ошибками

част- поиск

Фронт

Индив

Тема: Прогрессии (14 часов)

Интегрирующая дидактическая цель

Обучающие и интеллектуально-развивающие цели обеспечивают усвоение темы на уровне:

Знания – ученик должен знать:

- употребляемые термины (последовательность, арифметическая и геометрическая прогрессии, n- й член последовательности, разность арифметической прогрессии, знаменатель геометрической прогрессии);

- формулировки теорем, свойств, следствий из них по данной теме;

- формулы n –го членов арифметической и геометрической прогрессий, формулы сумму n первых членов арифметической и геометрической прогрессий

- алгоритм решения задач обязательного уровня с применением формул.

Понимания – ученик должен понимать:

- употребляемые термины, теоремы, формулы; алгоритм решения типовых задач.

Применения – ученик должен уметь:

- находить неизвестный член последовательности, зная формулу n – го члена;

- применять формулу n –го члена при решении задач, находить разность арифметической и знаменатель геометрической прогрессий:

- находить по формулу сумму n первых членов арифметической и геометрической прогрессий

Ученик может:

- научиться решать задачи прикладного характера;

- научиться составлять творческие задания.

Обобщения и систематизации знаний – ученик имеет возможность:

- решать задачи более сложного характера

- использовать приобретённые теоретические сведения для решения более сложных задач.

- переносить знания в смежные дисциплины

Воспитательные цели

Ученик:

- стремиться рационально организовать свой труд;

- повышает интерес к решению нестандартных задач;

- формирует у себя положительный мотив учения.

- развивает навыки устной речи, умение грамотно вести диалог;

- развивает образное мышление;

- осознаёт необходимость самостоятельных действий при решении проблем;

- осознанно перерабатывает полученные знания для выработки целостной системы знаний по данной теме;

№ п\п

Тема учебного занятия

пункт

Дата

Ко- во часов

Тип учебного занятия, форма его проведения

Дидактические цели урока

Методы обуч,

Формы позн деят

Межпред связи, наглядн

контроль

Лит-ра, образоват продукт

Последовательности

П 15

1 час

урок изучения нового мат.

Ученик должен знать: что называется последовательностью, что такое первый член последовательности, формула n –го членов последовательности

Ученик должен уметь: находить неизвестный член последовательности, зная формулу n –го членов последовательности; приводить примеры бесконечной и конечной последовательностей; приводить примеры последовательностей, заданных описанием, формулой n –го члена, рекуррентным способом; записывать формулу n –го члена, заданной перечислением её членов.

объяс-иллюст

Фронт

Таблица

№5/01

Составить задания с кодированным ответом

Определение арифметической прогрессии. Формула n –го члена арифметической прогрессии.

П 16

1 час

урок изучения нового мат.

Ученик должен знать: определение арифметической прогрессии, формулу n –го члена арифметической прогрессии, формулировку теоремы о том. что последовательность (a_n), заданная формулой a_n= kx+b, является арифметической прогрессией.

Ученик должен уметь: применять формулу n –го члена арифметической прогрессии при решении задач, находить разность арифметической прогрессии;

выводить формулу n –го члена арифметической прогрессии;

доказывать теорему о том. что последовательность (a_n), заданная формулой a_n= kx+b, является арифметической прогрессией.

объяс-иллюст

Фронт

Индив

Таблица

Презент

«Ариф.прогрессия»

Сам раб

№10/

2000

№36/01 стр 38

Формула суммы n первых членов арифметической прогрессии

П 17

2 часа

1) урок изучения нового мат.

2) урок закр знаний и ум

Ученик должен знать формулу суммы членов арифметической прогрессии в двух вариантах

Ученик должен уметь: находить по формуле сумму n первых членов арифметической прогрессии; решать задачи различной степени трудности по изученной теме.

1) объяс-иллюст

Фронт

индивид

2)част- поиск

Фронт

Индив

Обобщающий урок по теме «арифметическая прогрессия»

1 час

Урок обобщения и систем знаний и умений

Ученик должен знать вопросы теории по изученной теме.

част- поиск

Фронт

Индив

тест

Контрольная работа № 1 по теме «арифметическая прогрессия»

1 час

Урок контроля знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Метод письменного контроля

индивид

к/р

Анализ контрольной работы

1 час

Урок коррекции знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Ученик должен уметь анализировать результаты своей деятельности, проводить работу над ошибками

част- поиск

Фронт

Индив

Определение геометрической прогрессии

п 18

1 час

урок изучения нового мат.

Ученик должен знать: определение геометрической прогрессии; что называется знаменателем геометрической прогрессии; формулу n –го члена геометрической прогрессии

Ученик должен уметь: находить знаменатель геометрической прогрессии; n–й член геометрической прогрессии, зная первый член геометрической прогрессии и знаменатель и наоборот; решать задачи различной степени трудности

объяс-иллюст

Фронт

Таблица

№11/02 стр 15

Формула суммы n первых членов геометрической прогрессии

п 19

1 час

урок изучения нового мат.

Ученик должен знать формулы суммы n первых членов геометрической прогрессии.

Ученик должен уметь выводить и применять формулы суммы n первых членов геометрической прогрессии при решении задач различной степени трудности

объяс-иллюст

Фронт

Сумма бесконечной убывающей геометрической прогрессии при

п 20

1) урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать формулу суммы бесконечно убывающей геометрической прогрессии.

Ученик должен уметь применять формулу суммы бесконечно убывающей геометрической прогрессии при решении задач различного уровня сложности.

1) объяс-иллюст

Фронт

индивид

2)част- поиск

Фронт

Индив

Составить задания с кодированным ответом

10.

Обобщающий урок по теме «Геометрическая прогрессия»

1 час

Урок обобщения и систем знаний и умений

Ученик должен знать вопросы теории по изученной теме.

част- поиск

Фронт

Индив

Урок «Сравнение ар. и геом.

прогрессий»

тест

№46/

2000 стр13

11.

Контрольная работа № 1 по теме «Геометрическая прогрессия»

1 час

Урок контроля знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Метод письменного контроля

индивид

к/р

№ 17/ 2000

12.

Анализ контрольной работы

1 час

Урок коррекции знаний и умений

Ученик должен знать вопросы теории по изученной теме.

Ученик должен уметь анализировать результаты своей деятельности, проводить работу над ошибками

част- поиск

Фронт

Индив

Тема: Комбинаторные задачи. Вероятность случайного события. (12 часов)

Интегрирующая дидактическая цель

Обучающие и интеллектуально-развивающие цели обеспечивают усвоение темы на уровне:

Знания – ученик должен знать:

- употребляемые термины ();

- методы решения задач по теме «»

Понимания – ученик должен понимать:

-употребляемые термины;

- алгоритм исследования квадратичной функции.

Применения – ученик должен уметь:

- правильно употреблять символику и терминологию;

.Ученик может:

- усвоить приёмы решения задач различной степени трудности

- научиться решать задачи по теме «Вероятность случайного события» различными способами.

Обобщения и систематизации знаний – ученик имеет возможность:

- получить дополнительные исторические сведения;

- использовать приобретённые теоретические сведения для решения более сложных задач.

Воспитательные цели

Ученик:

- развивает навыки устной речи, умение грамотно вести диалог;

- развивает образное мышление;

- осознаёт необходимость самостоятельных действий при решении проблем;

- осознанно перерабатывает полученные знания для выработки целостной системы знаний по данной теме;

- развивает общие навыки учебной деятельности;

- строит собственные планы в соответствии с собственными способностями, интересами, убеждениями;

- проявляет интерес к сотрудничеству в групповой работе.

№ п\п

Тема учебного занятия

пункт

Дата

Ко- во часов

Тип учебного занятия, форма его проведения

Дидактические цели урока

Методы обуч,

Формы позн деят

Межпред связи, наглядн

контроль

Лит-ра, образоват продукт

Примеры комбина

торных задач

П.

2 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать: различные способы решения комбинаторных задач (перебор возможных вариантов, комбинаторное правило умножения)

Ученик должен уметь: решать задачи различной степени сложности, строя дерево возможных вариантов, используя комбинаторное правило умножения

Решать задачи на уровне выше стандарта.

Решать задачи повышенной трудности.

1) объяс-иллюст

Фронт

2) репрод фронт индив

Презен

тация

Сам раб

Задачник комбинаторных задач

Переста

новки

П 31

2 часа

1)урок изучения нового мат.

2) Урок закрепл знан и умен

Ученик должен знать: определение перестановки из n элементов, понятие факториала, формулу всевозможных перестановок из n элементов.

Ученик должен уметь : решать задачи различной степени сложности по данной теме, находить значения выражений, содержащих умножение и деление факториалов.

Решать задачи на уровне выше стандарта.

Решать задачи повышенной трудности.

1) объяс-иллюст

Фронт

индив 2) репрод фронт индив

Презен

тация

Сам раб

Размеще

ния

П 32

1 час

1) урок изучения нового мат.

Ученик должен знать: определение размещения из n элементов по k , формулу для вычисления числа размещений из n элементов по k (k ≤ n) .

Ученик должен уметь: решать задачи различной степени сложности по данной теме.

Решать задачи на уровне выше стандарта.

Решать задачи повышенной трудности.

1)объяс-иллюст

Фронт

индивид 2)част- поиск

Фронт

Индив

Сам раб

Сочета

ния

П 33

2 часа

1) урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать: определение сочетания из n элементов по k , Формулу для вычисления числа сочетаний из n элементов по к при любом k ≤ n.

Ученик должен уметь решать задачи различной степени трудности по изученной теме.

Решать задачи на уровне выше стандарта.

Решать задачи повышенной трудности.

объяс-иллюст

Фронт

индивид

Презен

тация

Диктант

Сам раб

Относи

тельная частота случайного события.

Вероят

ность равновозможных событий

п 34-

2 часа

1)урок изучения нового мат.

2)урок закр знаний и ум

Ученик должен знать: определение частоты рассматриваемого события, относительной частоты случайного события в серии испытаний, понятие благоприятных исходов события, как вычислить вероятность события в проводимом испытании.

Ученик должен уметь: применять полученные знания при решении задач различной степени трудности.

Решать задачи на уровне выше стандарта.

Решать задачи повышенной трудности.

объяс-иллюст

Фронт

Презентация

Обобщающий урок по теме «»

1 час

Урок обобщения и систем знаний и умений

Ученик должен знать вопросы теории по изученной теме.

част- поиск

Фронт