Муниципальное казённое образовательное учреждение

«Средняя общеобразовательная школа №3»

г. Исилькуля Омской области

Тест

«Решение вероятностных задач»

Подготовила: учитель математики Зинченко Елена Владимировна

2013 г.

В связи с введением в школьный стандарт математического образования элементов теории вероятностей и математической статистики возникла острая необходимость отслеживать усвоение пройденного материала: умение решать простейшие задачи методом перебора, а также с использованием известных формул, вычислять в простейших случаях вероятности событий на основе подсчета числа исходов.

Данная работа поможет в организации контроля в тестовой форме на уроке по теме «Решение вероятностных задач с помощью комбинаторики» по учебнику Ш.А. Алимова, Ю.М. Колягина и др. «Алгебра 9 класс», а также его можно использовать при подготовке к ГИА. Тест представлен в двух вариантах.

Ключ к тесту:

№ задания

I вариант

II вариант

1.

3

4

2.

4

2

3.

4

1

4.

1

2

5.

1

4

6.

0,35

0,6

7.

0,2

0,2

8.

0,1

0,1

9.

0,2

0,25

10.

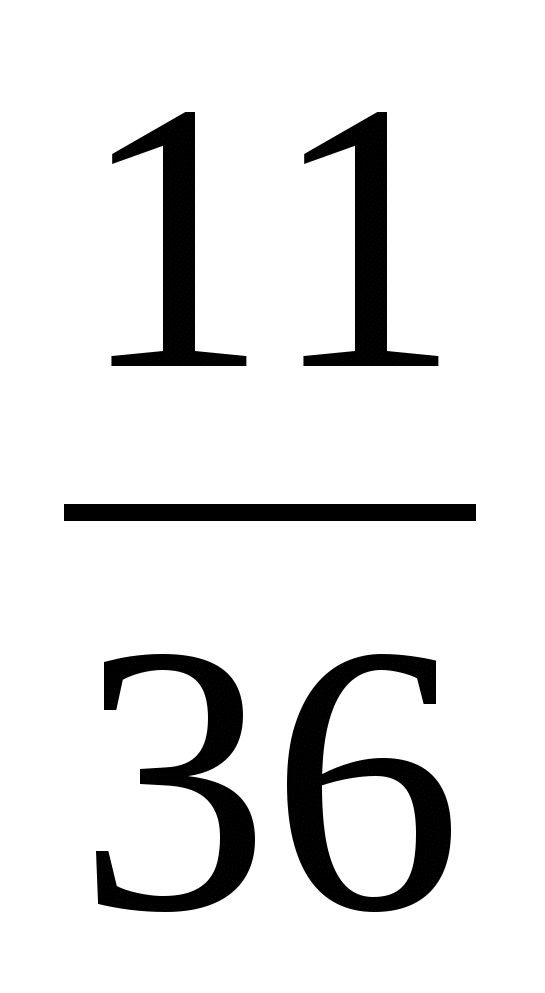
0,75

Решение вероятностных задач

Вариант 1.

При выполнении заданий 1-5 укажите номер правильного ответа.

1.    Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?

1) 30    2) 100      3) 120        4) 5

2. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?

1) 10         2) 60          3) 20                     4) 30

3. В денежно-вещевой лотерее на 1000000 билетов разыгрывается 1200 вещевых и 800 денежных выигрышей. Какова вероятность выигрыша?

1) 0,02 2) 0,00012                 3)0,0008                        4) 0,002

4. В игральной колоде 36 карт. Наугад выбирается одна карта. Какова вероятность, что эта карта – туз?

1) 2) 3) 4)

5. Бросают два игральных кубика. Какова вероятность того, что выпадут две четные цифры?

1) 0,25 2)   3) 0,5 4) 0,125

При выполнении заданий 5-10 укажите только ответы.

6. В закрытую коробку помещены 20 шаров: 8 из них – белые, 5 – черные, остальные красные. Какова вероятность того, что вытаскивая шары из коробки вслепую, первым мы извлечем из нее красный шар?

7. В саду решили посадить саженцы груш, абрикосов и яблонь, соответственно 5,7 и 3 штуки. Чему равна вероятность выбрать наугад саженец яблони?

8. Выбрано трехзначное число. Найдите вероятность того, что оно оканчивается на 3.

9. Наугад называется натуральное число от 1 до 30. Какова вероятность того, что это число кратно 5?

10. Брошены две игральные кости. Какова вероятность того, что хотя бы на одной кости появятся 3 очка?

Решение вероятностных задач

Вариант 2.

При выполнении заданий 1-5 укажите номер правильного ответа.

1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?

 1) 100         2) 30         3) 5                  4) 120

2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?

1) 3             2) 6           3) 2                  4) 1

3. В денежно-вещевой лотерее на 1000000 билетов разыгрывается 1500 вещевых и 500 денежных выигрышей. Какова вероятность выигрыша?

1) 0,002 2) 0,00012                 3)0,0008                        4) 0,02

4. Какова вероятность, что при одном броске игрального кубика выпадает число очков, равное четному числу?

1)   2) 0,5 3) 4) 0,25

5. Бросают два игральных кубика. Какова вероятность того, что выпадут две нечетные цифры?

1) 0,125 2)   3) 0,5 4) 0,25

При выполнении заданий 5 - 10 укажите только ответы.

6. В магазине с системой самообслуживания на витрине лежат 30 пирожков, из них 9 – с сыром, 3 – с мясом, а остальные – с печенью. Алексей наудачу взял один пирожок. Какова вероятность того, что выбранный им пирожок оказался с печенью?

7. На книжной полке выставлена художественная литература: 3 тома произведений А.С. Пушкина, 5 томов А.П. Чехова и 7 книг по современной поэзии. Какова вероятность того, что наугад взятая книга будет томом А.С. Пушкина?

8. Выбрано пятизначное число. Найдите вероятность того, что оно оканчивается 5.

9. Наугад называется натуральное число от 1 до 20. Какова вероятность того, что это число кратно 4?

10. Брошены две игральные кости. Какова вероятность того, что хотя бы на одной кости появится четное число очков?

 

Источники информации:

1. Ш.А. Алимова, Ю.М. Колягина и др. «Алгебра 9 класс», Москва, Просвещение, 2010 г

2. Ф.Ф. Лысенко, С.Ю. Кулабухов «Математика – 9 класс. Подготовка к ГИА – 2013», Ростов-на-Дону, Легион, 2012г.

3. Ф.Ф. Лысенко «Алгебра – 9 класс. Подготовка к итоговой аттестации – 2009», Ростов-на-Дону, Легион, 2009г.