Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №3

Станица Старощербиновская Щербиновского района Краснодарского края

Задачи на смеси и сплавы

ЕГЭ Задание В13

Подготовила: учитель математики

Категория: высшая

Тихончук Людмила Юрьевна

2013г.

Задачи на смеси и сплавы традиционно являются слабым звеном в подготовке школьников к ЕГЭ, кажутся многом из них довольно сложным. В таких задачах речь идет о растворах некоторого вещества в другом веществе и об изменении концентрации этого вещества после каких-либо манипуляций. При этом водные растворы, смеси или сплавы играют исходные роли и позволяют лишь несколько разнообразить сюжеты задач без изменений математического содержания. Ключевой идеей при решении таких задач является идея отслеживания изменений.

Предлагаю более простой способ решения данного типа задач с применением химической формулы

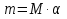, где

m-количество чистого вещества

M-количество всего вещества

d-доля ( процентная, выраженная в десятичной дроби)

Используемая таблица

m

(m=M∙d)

M

d

1

2

3

Задачи с решениями:

1.В 1 кг сплава меди и олова содержится 45% олова. Сколько граммов меди надо добавить к этому сплаву, чтобы процентное содержание олова в новом сплаве стало равным 15%?

Пусть х- количество граммов меди, которое необходимо добавить к сплаву.

Заполним таблицу :

В 1 кг сплава меди и олова содержится 45% олова.

1кг=1000г

m

(m=M∙d)

M

d

1

1000г

0,45(олово)

2

3

Сколько граммов меди надо добавить к этому сплаву

m

(m=M∙d)

M

d

1

1000г

0,45(олово)

2

+хг

0

3

чтобы процентное содержание олова в новом сплаве стало равным 15%?

m

(m=M∙d)

M

d

1

1000г

0,45(олово)

2

+хг

0

3

1000+х

0,15

Заполним второй столбец используя формулу

m

(m=M∙d)

M

d

1

450

1000г

0,45(олово)

2

0

+хг

0

3

(1000+х)∙0,15

1000+х

0,15

Пологая, что 1 действие+2 действие=3 результат, составим и решим линейное уравнение:

450+0=(1000+х)∙0,15

450=150+0,15х

Х=2000г Ответ: 2000

Учитываем, что добавили, долили- это «+», а отлили, испарили- это «-».

2.В лаборатории изготовили 1кг 16% солевого раствора. Через неделю из этого раствора испарилось 200г воды. Определите процентное содержание соли в новом растворе.

m

(m=M∙d)

M

d

1

160

1000г

0,16(соль)

2

0

-200г

0

3

800х

800г

х

160-0=800х

Х=0,2

0,2=20% Ответ:20

3.Морская вода содержит 4% (по массе) соли. Сколько килограммов чистой воды надо выпарить из 30 кг морской воды, чтобы содержание соли в последней составляло 12 %?

m

(m=M∙d)

M

d

1

1,2

30кг

0,04(соль)

2

0

-х

0

3

(30-х)∙0,12

30-х

0,12

1,2-0=(30-х)∙0,12

1,2=3,6-0,12х

Х=20 кг Ответ :20

4.Сколько граммов воды нужно добавить к 700 граммам 12 %-ного уксусного раствора, чтобы получить 7 %-ный ?

m

(m=M∙d)

M

d

1

84

700г

0,12(уксус)

2

0

+х

0

3

(700+х)∙0,07

700+х

0,07

84+0=(700+х)∙0,07

84=49+0,07х

Х=500г Ответ:500

5.Морская вода содержит 6% (по массе) соли. Сколько килограммов чистой воды надо выпарить из 80 кг морской воды, чтобы содержание соли в последней составляло 8 %?

m

(m=M∙d)

M

d

1

4,8

80

0,06(соль)

2

0

-х

0

3

(80-х)∙0,08

80-х

0,08

4,8-0=(80-х)∙0,08

4,8=6,4-0,08х

Х=20кг Ответ: 20

6.Слиток сплава меди и цинка массой 1 кг содержит 42% меди. Сколько граммов цинка надо добавить к этому куску, чтобы полученный сплав содержал 20% меди?

m

(m=M∙d)

M

d

1

420

1000

0,42(медь)

2

0

+х

0

3

(1000+х)∙0,2

1000+х

0,2

420+0=(1000+х)∙0,2

420=200+0,2х

Х=1100г Ответ: 1100

7.В лаборатории изготовили 1кг 24% солевого раствора. Через неделю из этого раствора испарилось 200г воды. Определите процентное содержание соли в новом растворе.

m

(m=M∙d)

M

d

1

240

1000

0,24(соль)

2

0

-200

0

3

800х

800

х

240-0=800х

Х=0,3

0,3=30% Ответ: 30

8.Морская вода содержит 5% (по массе) соли. Сколько килограммов пресной воды надо прибавить к 40 кг морской воды, чтобы содержание соли в последней составляло 2 %?

m

(m=M∙d)

M

d

1

2

40

0,05(соль)

2

0

+х

0

3

(40+х)∙0,02

40+х

0,02

2+0=(40+х)∙0,02

2=0,8+0,02х

Х=60кг Ответ:60

9.В лаборатории изготовили 1кг 12% солевого раствора. Через неделю из этого раствора испарилось 400г воды. Определите процентное содержание соли в новом растворе.

m

(m=M∙d)

M

d

1

120

1000

0,12(соль)

2

0

-400

0

3

600х

600

х

120-0=600х

Х=0,2

0,2=20% Ответ: 20

10.Сколько граммов воды нужно добавить к 500 граммам 16 %-ного уксусного раствора, чтобы получить 10 %-ный ?

m

(m=M∙d)

M

d

1

80

500

0,16(уксус)

2

0

+х

0

3

(500+х)∙0,1

500+х

0,1

80+0=(500+х)∙0,1

80=50+0,1х

Х=300г Ответ: 300

11.Имеется 10 литров 60-процентного раствора соли. Сколько литров воды нужно долить, чтобы получить 40-процентный раствор соли?

m

(m=M∙d)

M

d

1

6

10

0,6 с

2

0

+х

О с

3

4+0,4х

10+х

0,4

6+0=4+0,4х

Х=5 Ответ:5

12.Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы, содержащий 1/12 часть олова, сплавляется с другим куском, содержащим 1/10 часть олова. Полученный сплав содержит 1/11 часть олова. Найдите вес второго куска, если вес первого равен 84 кг.

m

(m=M∙d)

M

d

1

7

84

1/12

2

1/10х

+х

1/10

3

84/11+1/11х

84+х

1/11

7+1/10х=84/11+1/11х

х=70 Ответ:70

13.У хозяйки есть 5 литров сахарного сиропа 50% концентрации. Сколько литров воды необходимо добавить для получения сиропа 20% концентрации?

m

(m=M∙d)

M

d

1

2,5

5

0,5 с

2

0

+х

0

3

1+0,2х

5+х

0,2 с

2,5+0=1+0,2х

Х=7,5 Ответ:7,5

14. Имеется два сплава с разным содержанием меди: в первом содержится 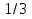,а во втором – 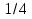меди. Сплавили 3 кг первого и 2 кг второго сплава, какую часть меди содержит новый сплав?

m

(m=M∙d)

M

d

1

1

3

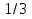
2

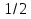
+2

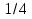
3

5х

5

х

1+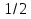=5х

Х=0,3 Ответ:0,3

15. Для консервирования 10 кг баклажан необходимо 0,5 л столового уксуса (10 % раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80 % раствор уксусной кислоты), из которой она готовит уксус, добавляя в нее воду. Сколько миллилитров уксусной эссенции понадобится хозяйке для консервирования 20 кг баклажан?

m

(m=M∙d)

M

d

1

0,4-0,8х

0,5-х

0,8

2

0

+х

0

3

0,05

0,5

0,1

0,4-0,8х+0=0,05

Х=0,4375 – воды

0,5-0,4375=0,0625 л эссенции на 10 кг, на 20 кг – 0,125 л или 125 мл Ответ:125

16. Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы весом 96 кг, содержащий 1/12 часть олова, сплавили с другим куском, содержащим 1/10 часть олова. Сколько килограмм весит второй кусок, если полученный сплав содержит 1/11 часть олова?

m

(m=M∙d)

M

d

1

8

96

1/12

2

1/10х

+х

1/10

3

96/11+1/11х

96+х

1/11

8+1/10х=96/11+1/11х

х=80

Ответ:80

17. Смешали 30 %-ный раствор соляной кислоты с 10 %-ным и получили 600 г 15 %-ного раствора. Сколько граммов первого раствора было взято?

m

(m=M∙d)

M

d

1

0,3х

х

0,3 к

2

60-0,1х

600-х

0,1 к

3

90

600

0,15

0,3х+60-0,1х=90

х=150 Ответ:150

8. В одном литре медицинского этилового спирта содержится 40 мл воды. Долив в него дистиллированной воды, врач получил раствор, содержащий 2/5 части спирта. Найдите объем (в мл) получившегося раствора?

m

(m=M∙d)

M

d

1

960

1000

0,96 с

2

0

+х

0

3

400+0,4х

1000+х

2/5 ( 0,4)

960+0=400+0.4х

Х=1400 мл добавлено

1400+1000=2400мл – всего Ответ:2400

19. Свежая клюква состоит на 99 % из воды. Заготовители собрали 500 кг клюквы и сдали ее на склад. После длительного хранения на складе содержание воды в клюкве уменьшилось до 96 %. Сколько килограммов весит клюква после хранения?

m

(m=M∙d)

M

d

1

5

500

0,01 к

2

0

-х

0

3

20-0,04х

500-х

0,04

5+0=20-0,04х

Х=375кг потеря при хранении

500-375=125кг после хранения Ответ:125

20. Кусок сплава меди и цинка массой в 36 кг содержит 45 % меди. Сколько килограммов меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60 % меди?

m

(m=M∙d)

M

d

1

16,2

36

0,45 м

2

х

+х

1 м

3

21,6+0,6х

36+х

0,6 м

16,2+х=21,6+0,6х

Х=13,5 Ответ:13,5

21. Свежие абрикосы содержат 80 % воды по массе, а курага (сухие абрикосы) – 12 % воды. Сколько понадобится килограммов свежих абрикосов, чтобы получить 10 кг кураги?

m

(m=M∙d)

M

d

1

8+0,8х

10+х

0,8

2

х

-х

1

3

1,2

10

0,12

8+0,8х-х=1,2

Х=34 потеря при хранении

34+10=44кг Ответ:44

22. По рецепту засолки огурцов на каждые 10 л рассола необходимо добавить 1 л столового уксуса (10 % раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80 % раствор уксусной кислоты), из которой она готовит уксус, добавляя в нее воду. Сколько миллилитров уксусной эссенции понадобиться хозяйке для приготовления 5 л рассола?

m

(m=M∙d)

M

d

1

0,8-0,8х

1-х

0,8

2

0

+х

0

3

0,1

1

0,1

0,8-0,8х+0=0,1

Х=0,875 л воды

1-0,875=0,125л эссенции на 10 л

62,5 мл на 5 л Ответ:62,5

23. Кислый маринад для консервирования овощей содержит 24% столового уксуса (10 % раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80 % раствор уксусной кислоты). Сколько процентов уксусной эссенции должно содержаться в аналогичном маринаде?

m

(m=M∙d)

M

d

1

0,192-0,8х

0,24-х

0,8 к

2

0

+х

0

3

0,024

0,24

0,1

0,192-0,8х+0=0,024

Х=0,21 или 21% воды 24%-21%=3% Ответ:3

24. Имеется лом стали двух сортов с содержанием никеля 5 % и 40 %. Сколько нужно взять металла первого из этих сортов, чтобы получить 140 т стали с содержанием 30 % никеля?

m

(m=M∙d)

M

d

1

0,05х

х

0,05

2

56-0,4х

+140-х

0,4

3

42

140

0,3

0,05х+56-0,4х=42

Х=40т Ответ:40

25. Свежесрезанные грибы содержат 90 % воды. После длительного хранения 120 кг грибов на складе содержание воды в них уменьшилось до 84 %. Какой стала масса грибов после хранения?

m

(m=M∙d)

M

d

1

108

120

0,9 в

2

х

-х

1 в

3

100,8-0,84х

120-х

0,84

108-х=100,8-0,84х

Х=45 кг потеря при хранении

120-45=75 кг осталось. Ответ:75

26.Смешали 40%-ый раствор соляной кислоты с 10%-ым и получили 500 мл 28%-го

раствора. Сколько мл 40%-го раствора было взято?

m

(m=M∙d)

M

d

1

0,4х

х

0,4 к

2

50-0,1х

500-х

0,1 к

3

140

500

0,28

0,4х+50-0,1х=140

0,3х=90

Х=300 Ответ:300

27.Хозяйка приготавливает уксус путем добавления воды в 70%-ю уксусную

эссенцию. Сколько мл эссенции нужно взять для приготовления 1,4 л 6%-го уксуса?

m

(m=M∙d)

M

d

1

0

1400-х

0

2

0,7х

+х

0.7

3

84

1400

0,06

0+0,7х=84

0.7х= 84

Х=120 Ответ:120

28.Хозяйка приготавливает уксус путем добавления воды в 70%-ю уксусную

эссенцию. Сколько мл воды нужно добавить на 210 мл эссенции, чтобы получился

раствор 6%-го уксуса?

m

(m=M∙d)

M

d

1

147

210

0,7

2

0

+х

0

3

12,6+0,06х

210+х

0,06

147=12,6+0,06х

Х=2240 Ответ:2240

Список использованной литературы

1.ЕГЭ 2012 Математика .Задача В13.Задачи на составление уравнений. Рабочая тетрадь

Под редакцией А.Л.Семенова и И.В.Ященко М: издательство: МЦНМО 2012г.

2. Тексты КДР 2010-2013 г . Автор составитель: Краснодарский краевой институт дополнительного профессионального педагогического образования.