Методи обчислення дисперсії

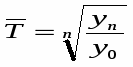
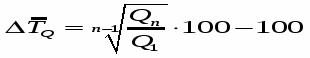
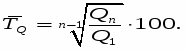
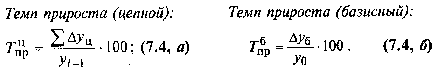
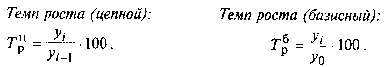
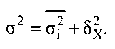
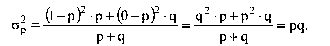
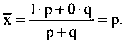
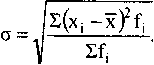
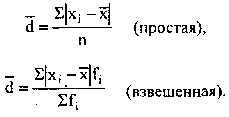План

Методи обчислення дисперсії
Задача №6
Задача №12
Задача №18
Задача №24

1. Методи обчислення дисперсії

Статистична дисперсія (від англ. statistical dispersion) — ступінь відхилення або зміни значень змінній від центрального пункту. Статистична дисперсія розраховується як різниця між значенням середньою квадратів варіюючої ознаки і квадратом середнього значення цієї ознаки. Дисперсія є базовим інструментом для статистичної оцінки варіації розподілу. Якщо значення ознаки розподілу ідентичні, то дисперсія рівна нулю. Дисперсія не може бути негативною величиною.

Умови існування і розвитку окремих одиниць сукупності певною мірою різні, що позначається і на відмінності значень у них узятої нами ознаки. Середня величина відображає ці середні умови.

Середнє лінійне відхилення дає узагальнену характеристику ступеня тієї, що коливається ознаки в сукупності. Проте при його численні доводиться допускати некоректні з погляду математики дії, порушувати закони алгебри, що спонукало математиків і статистиків шукати інший спосіб оцінки варіації для того, щоб мати справу тільки з позитивними величинами. Найпростіший вихід - звести всі відхилення в другий ступінь.

Отримана міра варіації називається дисперсією, а корінь квадратний з дисперсії - середнім квадратичним відхиленням. Ці показники є загальноприйнятими заходами варіації і часто використовуються в статистичних дослідженнях, а також в техніці, біології і інших галузях знань. Дані показники знайшли також своє широке застосування в міжнародній практиці обліку і статистичного аналізу, зокрема в системі національного рахівництва.

Середнє квадратичне відхилення - це узагальнююча характеристика розмірів варіації ознаки в сукупності. Воно виражається в тих же одиницях вимірювання, що і ознака (у метрах, тоннах, рублях, відсотках і т. д.).

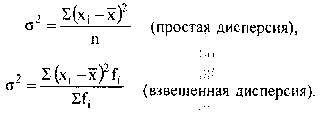
Дисперсія - середній квадрат відхилень індивідуальних значень ознаки від їх середньої величини.

Серед безлічі варіюючих ознак, що вивчаються статистикою, існують ознаки, якими володіють одні одиниці сукупності і не володіють інші. Ці ознаки називаються альтернативними. Прикладом таких ознак є: наявність бракованої продукції, вчений ступінь у викладача вузу, робота по отриманій спеціальності і так далі. Варіація альтернативної ознаки кількісно виявляється в значенні нуля у одиниць, які цією ознакою не володіють, або одиниці у тих, які дану ознаку мають.

Хай р - частка одиниць в сукупності, що володіють даною ознакою (р = m/n); q - частка одиниць, що не володіють даною ознакою, причому р + q = 1. Альтернативну ознаку приймає всього два значення - 0 і 1 з вагами відповідно q і р. Обчислений середнє значення альтернативної ознаки по формулі середньої арифметичної:

Дисперсія альтернативної ознаки визначається по формулі:

Таким чином, дисперсія альтернативної ознаки рівна твору частки на доповнюючи цю частку до одиниці число. Корінь квадратний з цього показника відповідає середньому квадратичному відхиленню альтернативної ознаки.

Показники варіації альтернативних ознак широко використовуються в статистиці, зокрема при проектуванні вибіркового спостереження, обробці даних соціологічних обстежень, статистичному контролі якості продукції, у ряді інших випадків.

Буває необхідно прослідкувати кількісні зміни ознаки по групах, на які розділяється сукупність, а також і між групами. Таке вивчення варіації досягається за допомогою обчислення і аналізу різних видів дисперсії.

Виділяють дисперсію загальну, міжгрупову і внутрішньогрупову. Загальна дисперсія вимірює варіацію ознаки у всій сукупності під впливом всіх чинників, що зумовили цю варіацію.

Існує закон, що зв'язує три види дисперсії. Загальна дисперсія рівна сумі середньої з внутрішньогрупових і міжгруповою дисперсій:

Дане співвідношення називають правилом складання дисперсій. Згідно цьому правилу, загальна дисперсія, що виникає під дією всіх чинників, рівна сумі дисперсії, що з'являється під впливом всіх інших чинників, і дисперсії, що виникає за рахунок группировочного ознаки.

Знаючи будь-які два види дисперсій, можна визначити або перевірити правильність розрахунку третього вигляду.

2. Задача №6

Виробництво хімічних волокон і ниток становили, в млн. грн.:

2003 р.

2004 р.

2005 р.

Штучні волокна і нитки

2,3

1,6

3,5

Синтетичні волокна і нитки

2,7

2,4

4,8

Визначити по кожному волокну:

Базисні та ланцюгові темпи зростання та приросту.
Середньорічні темпи зростання та приросту.

Здійснити аналіз:

Зміни виробництва волокон по відношенню до минулого року.
Зміни виробництва волокон по відношенню до базисного року.

Среднегодовой темп роста выпуска товаров:

Среднегодовой темп прироста выпуска товаров:

Показатели

Год

у_ц

у_б

Т_ц

Т_б

Т_ц

Т_б

2003

-----

2004

-0,7

69,56

-30,43

-0,3

88,89

-11,11

2005

1,9

1,2

218,75

152,17

118,75

52,17

2,4

2,1

200

117,78

100

77,78

Рассчитываем среднегодовые темп роста и темп прироста по формулам

Среднегодовой темп роста

3. Задача № 12

Є такі дані про чисельність населення України і виробництво цукру–піску:

Рік

1994 р.

1995 р.

1996 р.

Чисельність населення на початок року, млн.чол.

52,1

51,7

51,3

Виробництво цукру-піску, млн.т.

3,4

3,9

3,3

Обчисліть:

Середні рівні рядів динаміки;
Середньорічні абсолютні прирости зменшення і середньорічні темпи зростання (зниження). Проаналізуйте обчислені показники.

4. Задача № 18

Слюсарі ремонтного цеху у березні отримали таку заробітню платню:

З/п, грн.

204

212

215

225

240

244

250

260

Число слюсарів