ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА

ФАКУЛЬТЕТ УПРАВЛЕНИЯ

Контрольная работа

По «Экономико-математическим методам»

Фисай А.А.

студента2-го курса

заочной формы обучения

Москва 2009г

Вариант 2.

№1.

Исследовать методом Жордана - Гаусса систему линейных уравнений, в случае совместности системы найти общее решение, некоторое частое небазисное решение, все базисные решения, указав при этом опорные решения:

х₁+х₂-х₃+2х₄=2

-х₁+х₂-3х₃-х₄=1

3х₁-х₂+5х₃+4х₄=3.

Решение:

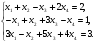
х₁

х₂

х₃

х₄

в_i

1

1

-1

2

2

-1

1

-3

-1

1

3

-1

5

4

3

1

1

-1

2

2

0

2

-4

1

3

0

-4

8

-2

-3

1

0

1

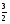
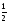
0

1

-2

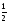
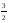
0

0

0

0

3

+II;∙ (-3)+III

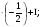∙ 2+III; :2

Получим эквивалентную систему уравнений

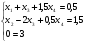
Последнее уравнение системы не имеет решений, исходная система несовместна, т.е. не имеет решений.

№2

Решить графическим методом следующие задачи линейного программирования: min f(x) = -6x₁+9x₂

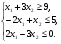
х₁, х₂ ≥0.

Решение.

(*)

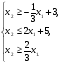х₁, х₂ ≥0.

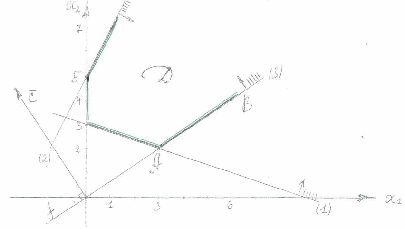
Построим граничные прямые

(1) 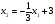х₁ 0 3

х₂ 3 2

(2) 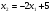х₁ 0 1

х₂ 5 7

(3) 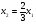х₁ 0 0

х₂ 0 2

Выбираем нужные полуплоскости (смотри (*))

Получим область решений Д.

Построим 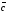=(-6;9); 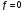- линия уровня, 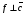. Параллельным переносом линии уровня определяем точки, в которых функция достигает минимума. Это все точки луча АВ прямой (3).

Задача имеет бесконечное множество решений. При этом значение функции ограничено и для любого X* 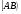составляем величину, равную 0.

Ответ: 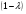(3;2) + 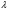(6;4), 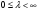; min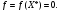

№3.

Решить симплексным методом следующие задачи линейного программирования min f(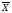) = - 2x₁ - 3x₂

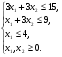
Решение.

f(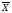) = - 2x₁ - 3x₂ + 0х₃ + 0х₄ +0х₅ 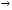min

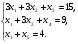
x_j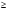0, j =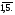

i

А_Б

С_Б

В

-2

-3

0

0

0

А₁

А₂

А₃

А₄

А₅

1

2

3

А₃

А₄

А₅

0

0

0

15

9

4

3

1

1

3

3

0

1

0

0

0

1

0

0

0

1

5

3_min

-

m+1

0

2

3

0

0

0

1

2

3

А₃

А₂

А₅

0

-3

0

6

3

4

2

⅓

1

0

1

0

1

0

0

-1

⅓

0

0

0

1

3_min

9

4

m+1

-9

1

0

0

-1

0

1

2

3

А₁

А₂

А₅

-2

-3

0

3

2

1

1

0

0

0

-

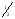
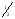
0

m+1

-12

0

0

0

-

-

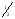
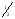
0

Все полученные оценки не положительны. План оптимален.

X* = (х₁ = 3; х₂ = 2)

f min = f (X*) = -2 ∙ 3 – 3 ∙ 2 = -12,

f min = -12.

Ответ: X* = (х₁ = 3; х₂ = 2);

f min = f (X*) = -12.

№4.

Решить следующие транспортные задачи (здесь А - вектор мощностей поставщиков, В – вектор мощностей потребителей, С - матрица транспортных издержек на единицу груза):

А = (300; 350; 160; 200), С = ;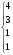

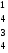
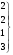В = (400; 400; 200),

Решение

н₁=0 н₂=1 н₃=-1

в_j

a_j

400

400

200

300

₄

300 ₁

₂

350

50 ₃

100 ₄

200 ₂

150

150 ₁

₃

₁

200

200 ₁

₄

₃

u₁ = 0

u₂ = 3

u₃ = 1

u₄ = 1

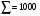
Опорное решение получили по правилу «минимальных издержек». Занятых клеток должно быть m + n – 1 = 4 + 3 – 1 = 6.

Определим потенциалы:

u₁ + н₂ = 1; u₂ + н₁ = 3; u₂ + н₂ = 4; u_{2 +} н₃ = 2;

u₃ + н₁ = 1; u₄ + н₁ = 1.

Пусть u₁ = 0, тогда u₂ = 3; u₁ = 0; u₃ = -1; u₃ = 1; u₄ = 1.

Оценки свободных клеток

Ѕ₁₁=4-(0+0)>0; Ѕ₁₃=2-(0-1)>0; Ѕ₃₂=3-(1+1)>0;

Ѕ₃₃=1-(1-1)>0; Ѕ₄₂=4-(1+1)>0; Ѕ₄₃=3-(1-1)>0.

План оптимален, т.к. все оценки положительны. Получим план перевозок

X* = ;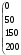

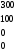
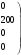минимальная стоимость Z min = Z (X*) = 300∙1 + 50∙3 + 100∙4 + ∙200∙2 + + 150∙1 + 200∙1 =∙1600.

№5.

Для выпуска четырех видов продукции требуются затраты сырья, рабочего времени и оборудования. Исходные данные приведены в таблице:

Тип

ресурса

Нормы затрат ресурсов на единицу продукции

Наличие

ресурсов

1

2

3

4

Сырье

Рабочее время

Оборудование

Прибыль на единицу продукции

3

22

10

30

5

14

14

25

2

18

8

8

4

30

16

16

60

400

128

Сформулировать экономико-математическую модель задачи на максимум прибыли и найти оптимальный план выпуска продукции.

Решение.

Обозначим через х₁, х₂, х₃, х₄ объем выпуска каждого из четырех видов продукции. Модель задачи примет вид: max Z = 30х₁ + 25х₂ + 8х₃ + 16х₄

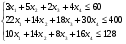
х_j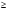0 (j = ).

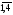Перейдем к задаче в каноническом виде:

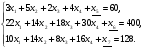
х_j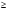0 (j = ).

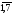i

А_Б

С_Б

В

30

25

8

16

0

0

0

А₁

А₂

А₃

А₄

А₅

А₆

А₇

1

2

3

А₅

А₆

А₇

0

0

0

60

400

128

3

22

10

5

14

14

2

18

8

4

30

16

1

0

0

0

1

0

0

0

1

20

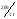
12,8

m+1

0

-30

-25

-8

-16

0

0

0

min

Z (X) = 30х₁ + 25х₂ + 8х₃ + 16х₄ + 0х₅ +0х₆ +0х₇ 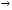max

i

А_Б

С_Б

В

30

25

8

16

0

0

0

А₁

А₂

А₃

А₄

А₅

А₆

А₇

1

2

3

А₅

А₆

А₇

0

0

30

21,6

118,4

12,8

0

0

1

0,8

-16,8

1,4

-0,4

0,4

0,8

-0,8

-5,2

1,6

1

0

0

0

1

0

-0,3

-2,2

0,1

m+1

384

0

17

16

32

0

0

3

Теперь все оценки не отрицательны. План оптимален.

Получили оптимальный план выпуска продукции X* = (12,8; 0; 0; 0). При этом максимальная прибыль составит

max Z = Z(X*) = 30∙12,8 + 25∙0 + 8∙0 + 16∙0 = 384.

Ответ: Следует выпускать только продукцию первого вида в количестве 12,8 ед. Максимальная прибыль составит 384 ден. ед.

14