КАФЕДРА

Экономической кибернетики

имитационное моделирование на основании предварительно установленных зависимостей.

г. Желтые Воды 2004

Содержание

1. Постановка задачи _________________________________ 3

2. Метод решения задачи _________________________________ 5

3. Программное решение _________________________________ 8

4. Руководство пользователя_______________________________ 11

5. Листинг программы _________________________________ 12

Постановка задачи

В современном мире гарантией эффективной работы любого предприятия служит рациональное использование денежных средств и трудового фактора. Так для расчета экономического эффекта работы кассового зала необходимо провести имитационное моделирование на основании предварительно установленных зависимостей.

Допустим, что клиенты в зал прибывают с интервалом, исчисляемым в минутах (см. рис. 1).

t

8⁰⁰

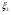
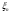
Рис. 1 – «Приход клиентов в зал»

Приход клиентов в зал описывается пуассоновским потоком с интенсивностью r, который определяется следующим образом:

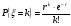(1.1)

где: r – интенсивность потока;

k – время между приходами клиентов.

Параметр k может принимать дискретные значения от нуля до бесконечности. Причем k=0 означает приход сразу двух клиентов.

Предположим, в зале имеется N касс. Математическое ожидание обслуживания клиентов в банке обозначим 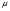. Обслуживание клиентов у касс происходит по экспоненциальному закону распределения случайной величины 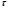( 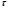- время обслуживания клиентов) с плотностью распределения :

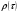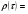
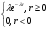(1.2)

Примечание:

Если в зале есть свободные кассы, то клиент становится на обслуживание к ближайшей из них (т.е. к кассе с минимальным номером). Если все кассы заняты – клиент становится в очередь к той кассе, где очередь минимальна. Если очереди одинаковы, то клиент становится в любую из них.

Для решения поставленной задачи необходимо разработать алгоритм имитационного моделирования работы кассового зала за 24-часовый рабочий день. А также определить время простоя касс и количество клиентов в очереди не обслуженных на момент закрытия банка.

1. Метод решения задачи

Имитационное моделирование на ЭВМ процесса функционирования автоматизированной системы управления работой кассового зала позволяет получить численное решение поставленной задачи. Суть рассматриваемого приближенного метода решения состоит в проведении ряда случайных испытаний вероятностной модели исследуемой системы и получении совокупности реализаций случайных процессов изменения состояния.

В результате многократной реализации случайных процессов определяются оценки вероятности тех или иных событий и средние значения случайных величин. Имитационное моделирование связано с необходимостью воспроизведения случайных событий и величин, распределенных по произвольному закону. Существует несколько способов генерации случайных величин и формирования их распределений. Модель системы управления работой кассового зала включает в себя:

• Приход клиентов в зал ;

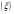• Время обслуживания клиентов у касс .

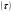По условию поставленной задачи приход клиентов в зал описывается пуассоновским потоком с интенсивностью r. Для лучшего понимания сути распределения Пуассона необходимо знать основные определения:

Интенсивность потока – среднее число событий, которое появляется в единицу времени.

Поток – последовательность событий, которые наступают в случайные моменты времени.

Закон распределения Пуассона выражается формулой (1.1).

Будем моделировать интервал времени между двумя последовательно зашедшими в банк клиентами методом Монте-Карло с датчиком случайных чисел на интервале [0 - 1].

Совокупность 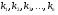независимых случайных событий, образующих полную группу, характеризуется вероятностями появления каждого из событий 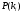, причем 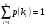. Для моделирования этой совокупности случайных событий используется генератор случайных чисел, равномерно распределенных в интервале [0 - 1]. При делении отрезка [0 - 1] на n частей, численно равных 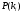, возникновение события устанавливается путем определения нахождения случайного числа Х в пределах интервала при проверке условия 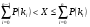, где 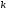изменяется от нуля до n. 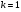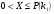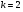При имеем ; при имеем 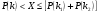и так далее. При подстановке в формулу (1.1) получим:

;

;

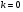
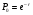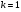
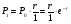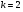
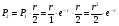и так далее.

Причем 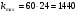(мин.) – максимальное количество ожидания клиентов.

Так как опыт проводится многократно, то, очевидно, что частота попадания случайных чисел на каждый из отрезков, определяющихся их длиной, и соответствует полученным вероятностям

Моделирование времени обслуживания клиентов у касс происходит по экспоненциальному закону распределения, формула которого представлена выше (формула (1.2)).

Время обслуживания клиентов 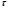, как и любая иная случайная величина, описывается функцией распределения 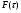, определяемая как вероятность 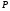случайного события, заключающегося в том, что время обслуживания клиентов 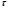меньше некоторого заданного времени :

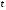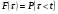
Эта вероятность рассматривается как функция 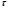во всем диапазоне возможных значений величины 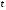. Функция распределения любой случайной величины является неубывающей функцией времени 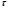. Примерный вид функции 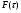дан на рисунке 3.

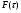
1

Рис. 3 – «Функция распределения экспоненциального закона»

Так как значения 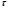не могут быть отрицательными, то 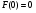. При 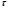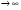величина 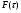стремится к единице. Таким образом, функция распределения времени обслуживания клиентов:

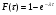(1.3)

где - параметр распределения (среднее время обслуживания клиентов у кассы).

Соответственно плотность распределения:

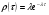(1.4)

Для моделирования времени обслуживания клиента у кассы проинтегрируем функцию распределения :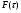

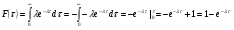
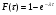(1.5)

От датчика случайных чисел равномерно распределенных на интервале [0 - 1] получаем очередное число Х, которое подставляем в формулу (1.5) и вычисляем :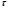

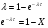
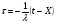(1.6)

Из соотношения (1.6) найдем 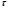соответствующее Х, которое будем принимать за случайное число, обозначающее время обслуживания данной кассой.

2. ПРОГРАММНОЕ РЕШЕНИЕ

Программа имитационного моделирования работы кассового зала написана на языке C с помощью среды разработки Borland C++ 3.1.

kassa

Блок-схема имитационного моделирования работы кассового зала

Ввод кол-ва касс m

Параметр распределения Пуассона

Ввод lambda

мин. и мак. время обслу- живания клиентов у касс

Ввод tau_min и tau_max

Время моделирования работы кассового зала в ч.

Ввод hours

Математическое ожи-дание и средн. кв. от-клонение

Ввод MO и SKO

Создание и обнуление массива и переменных

i : : = 1

Нет

current_time<=minutes

Да

Нет

current_time

Нет

i<=m

Да

Да

Да

Нет

tau[i]

t_free++

tau[i]--

i++

1

3

2

1

3

Нет

enter_time_<=current_time

2

Да

enter++

enter_time_=time_to()

i=1; INDPAS=1

Да

Нет

tau[i]

tau[i]=_tau()

INDPAS=0

i++

Да

i<=m && INDPAS= =1

Нет

Нет

Да

INDPAS= =1

refuse++

Да

INDPAS= =0

serve++

Нет

current_time++

stand=0; i=1

Нет

Да

tau[i]>0

stand++

i++

i

4

Коррек. кол-во обслуженных

Вычислим ср. время простоя

Вычислим ср. % обслуженных

Вычисл. ср. % необслуженных

serve-=stand;

t_free_av=(float)t_free/m; serve_av=(float)serve/enter;

refuse_av=(float)refuse/enter;

4

Вывод результатов

КОНЕЦ

Исходный текст программы состоит из одного файла Kas1.c который содержит реализацию таких функций программы:

– float RND_DIG (void) - Функция возвращающая СЧ в диапазоне [0, 1];

– void massive (void) - Функция выделяющая память под массив времени обслуживания у каждой из касс;

– float _tau(void) - Функция возвращающая время обслуживания у кассы;

– float time_to(void) - Функция определяет время входа следующего клиента. Промежутки между входами распределены по закону Пуассона с параметром lambda;

– void inf (void) - Функция вывода информации пользователю.

РУКОВОДСТВО пользователя

1. Программа имитационного моделирования работы банка расположена по следующему адресу:

A:\Kas1.exe

2. На запрос программы:

«Введите количество касс в кассовом зале ж\\д вокзала:»

Вводим предполагаемое (данное) количество касс обслуживающих клиентов.

3. На запрос программы:

«Введите параметр распределения Пуассона для определения времени между входами пассажиров в зал:»

Вводим lambda – Параметр распределения Пуассона

4. На запрос программы:

«Введите минимальную продолжительность обслуживания у касс»

Вводим tau_min – минимальную продолжительность обслуживания.

4. На запрос программы:

«Введите максимальную продолжительность обслуживания у касс»

Вводим tau_max – максимальную продолжительность обслуживания.

5. На запрос программы:

«Введите время моделирования работы зала(в ч.):»

Вводим hours - время моделирования работы зала.

6. На запрос программы:

«Введите математическое ожидание времени обслуживания у касс:»

Вводим MO - математическое ожидание.

7. На запрос программы:

«Введите среднеквадратическое отклонение времени обслуживания у касс:»

Вводим SKO - среднеквадратическое отклонение.

8. После просмотра результатов, нажмите любую клавишу для завершения работы.

5. Листинг программы

/* Включаемие модули*/

#include // Функции потокового ввода - вывода

#include // Формирование экракна

#include // Математические функции

#include // Функции по работе с динам. памятью

//Прототипы функций

float RND_DIG( void ); // Ф-я генерирует случ. числа

void inf( void); // Ф-я сообщает о назн-ии программы

void massive( void ); // Ф-я выделяющая память под массив

float _tau( void ); // Расчет времени обсл-я клиента у кассы

float time_to ( void ); // Расчет времени входа пассажира в зал

//Объявление переменных

float

tau_min, // Мин. время обсл-я у касс

tau_max, // Макс. время обсл-я у касс

*tau, // Тек. время обсл-я у касс

current_time, // Тек. время

minutes, // Общ. время работы в минутах

lambda, // Пар-р закона распр-я Пуассона

enter_time_, // Время входа очередного пассажира

MO, // Мат. ожид-е времени обсл-я

SKO, // Среднекв. откл-е времени обсл-я у касс

t_free, // Общ. время простоя касс

t_free_av, // Ср. время простоя

serve_av, // Ср. % обслуж-я пассажиров

refuse_av, // Ср. % отказов в обсл-ии

N0=7836, // 1-й множитель для расчета случ. числа

NI=4792, // 2-й множитель для расчета случ. числа

N, // Прозведение N0 и NI

ND; // Средние 4 цифры из числа N

int

m, // Кол-во касс

i, // Тек. номер кассы

enter, // Кол-во вошедших

hours, // Время работы зала в часах

serve, // Кол-во обслуж-х пассажиров

refuse, // Кол-во необслуж-х пассажиров

stand, // Кол-во стоящих в очереди на момент обслуживания

INDPAS; // Флаг обслуживания пассажиров

// Главная функция программы

void main(void)

{

inf(); // cообщение о назначении программы

textcolor( 14 ); //установка цвета и фона

textbackground( 1 );

clrscr(); //очистка экрана

/* Прием данных от пользователя */

printf("\n████████████████████████████████████████████████████████████████████████████████");

for(i=1;i<=21;i++)

printf("█ █");

printf("████████████████████████████████████████████████████████████████████████████████");

gotoxy(10,7);

do

{

printf("\n█\tВведите количество касс в кассовом"

" зале ж\\д вокзала:");

scanf( "%d", &m );

}

while( (m<=0)||(m>=100) );

do

{

printf( "\n█\tВведите параметр распределения Пуассона для"

" определения" );

printf( "\n█\t\tвремени между входами пассажиров в зал:" );

scanf( "%f", &lambda );

}while( lambda<=0 );

clrscr();

//Вывод рамки

printf("\n████████████████████████████████████████████████████████████████████████████████");

for(i=1;i<=21;i++)

printf("█ █");

printf("████████████████████████████████████████████████████████████████████████████████");

gotoxy(5,3);

do

{

printf( "\n█\n█\tВведите минимальную продолжительность обслуживания " );

printf( "\n█\t\t\tу кассами:" );

scanf( "%f", &tau_min );

}while( tau_min<=0 );

do

{

printf( "\n█\tВведите максимальную продолжительность обслуживания " );

printf( "\n█\t\t\tу касс:" );

scanf( "%f", &tau_max );

}while( tau_max<=tau_min );

do

{

printf( "\n█\tВведите время моделирования работы зала(в ч.):" );

scanf( "%d", &hours );

}while( hours<=0 );

do

{

printf("\n█\tВведите математическое ожидание времени обслуживания");

printf( "\n█\t\tу касс:");

scanf( "%f", &MO );

}while( MO<=0 );

do

{

printf( "\n█\tВведите среднеквадратическое отклонение времени ");

printf( "\n█\tобслуживания у касс:");

scanf( "%f", &SKO );

}while( SKO<=0 );

massive(); // создание и обнуление массива

minutes=floor( hours*60 ); // переведем время работы в минуты

enter=0; // никто не входил

serve=0; // никого не обслужили

refuse=0; // никому не отказали

t_free=0; // кассы еще не простаивали

current_time=0; // начало отсчета времени с нуля

enter_time_=time_to(); // когда зайдет следующий

/* Цикл моделирования работы зала

for( current_time=0; current_time<=minutes; current_time++ )

{

/* Коррект-ка времени обсл-я у каждой кассы */

if( current_time )

for( i=1; i<=m ;i++)

if( tau[i] ) //Если касса занята, то уменьшим время обсл-я

tau[i]--; // в ней на 1 мин.

else // Если касса свободна, наращиваем общее время

t_free++; // простоя касс.

if( enter_time_<=current_time )

{

enter++; // Если входит пассажир, отмечаем это

enter_time_=time_to(); // Узнаем, когда зайдет следующий?

i=1; // Вошедший подходит к 1-й кассе

INDPAS=1; // Его еще не обслуживают

do

{

if( tau[i]<=0 ) //Если касса свободна, ставим пассажира на

{ //обсл-е и узнаем, сколько ему стоять у кассы

tau[i]=_tau();

INDPAS=0; //Укажем, что пассажира обслуживают

}

i++; // Подходим к следующей кассе

}while((i<=m) && (INDPAS==1));

if( INDPAS==1 ) // Если клиент не обслужен, отмечаем это

refuse++;

if( INDPAS==0) // Если клиент обслужен, отмечаем это

serve++;

}

}

stand=0; // Пока в очереди никто не стоит

i=1; // Начинаем с первой кассы

do

{

if( tau[i]>0 ) // Если время обсл-я не равно нулю, значит

stand++; // у кассы кто-то стоит

i++; // Смотрим у следующей кассы

}while( i<=m );

serve-=stand; // Корректируем кол-во обслуженных

t_free_av=(float)t_free/m; // Вычислим ср. время простоя

serve_av=(float)serve/enter; // Вычислим ср. % обслуженных

refuse_av=(float)refuse/enter; // Вычислим ср. % необслуженных

textcolor(1); // Установка параметров текста

textbackground(2);

clrscr();

_setcursortype( _NOCURSOR );

/*Вывод полученных результатов

//Вывод рамки

printf("\n████████████████████████████████████████████████████████████████████████████████");

for(i=1;i<=21;i++)

printf("█ █");

printf("████████████████████████████████████████████████████████████████████████████████");

gotoxy(3,3);

printf( "\n█\n█\t╔════════════════════════════════════════════════════════════╗ ");

printf(" \n█\t║ %d железнодорожных касс работало на протяжении: %d часов.",m,hours );

gotoxy(70,6);

printf("║");

printf(" \n█\t║ В зал зашло %d посетителей.", enter );

gotoxy(70,7);

printf("║");

printf(" \n█\t║");

gotoxy(70,8);

printf("║");

printf(" \n█\t║\n█\t║ Было обслужено %d человек(а).", serve);

gotoxy(70,9);

printf("║");

printf(" \n█\n█\t║ Ушли необслуженными %d человек(а).", refuse);

gotoxy(70,10);

printf("║");

printf(" \n█\n█\t║ В очереди осталось стоять %d человек(а). ", stand);

gotoxy(70,11);

printf("║");

printf(" \n█\n█\t║ Средний процент обслуживания пассажиров %.2f%%", serve_av*100);

gotoxy(70,12);

printf("║");

printf(" \n█\n█\t║ Средний процент отказов в обслуживании %.2f%%", refuse_av*100);

gotoxy(70,13);

printf("║");

printf(" \n█\n█\t║ Всего кассы простаивали: %.0fч. %.0f мин. ",floor( t_free/60 ),

t_free-floor( t_free/60 )*60 );

gotoxy(70,14);

printf("║");

printf(" \n█\n█\t║ Среднее время простоя 1 кассы: %.0fч. %.0f мин.",

floor( t_free_av/60 ), t_free_av-floor( t_free_av/60 )*60);

gotoxy(70,15);

printf("║");

gotoxy(70,16);

printf("║");

printf(" \n█\t╚════════════════════════════════════════════════════════════╝ ");

getch();

}

//Функция возвращающая СЧ в диапазоне от 0 до 1

float RND_DIG (void)

{

float

x; //СЧ в диапазоне от 0 до 1

N=(NI*N0);

ND=floor(N/100);

ND=(ND/10000-floor(ND/10000))*10000; // Отбросим первые 2 цифры

N0=NI;

NI=ND;

x=ND/9999;

return x;

}

//Ф-я выделяет память под массив времени обсл-я у каждой из касс

void massive( void )

{

int i;

tau=(float *)malloc( (m+1)*sizeof(float) );

/* Обнуление элементов массива */

for(i=1; i<=m; i++)

tau[i]=0;

}

// Ф-я возвр. время обсл-я у кассы

float _tau( void )

{

float

x, // Случайное число x

y, // Случайное число y

z, // Случайное число z

tau_; // Время обслуживания

// Проверка на четность

//---------------------

if( floor ( ( float )i/2 )==ceil( ( float )i/2 ) )

{

x=RND_DIG(); // Запрос случ. числа от ДСЧ

y=RND_DIG(); // Запрос случ. числа от ДСЧ

if( x>=.0001) // Если х не слишком маленькое, считаем z

z=sqrt( -2*log( x ) )*sin( 2*M_PI*y );

else

{

if( sin( 2*M_PI*y )<=0 )

z=0; // Если оба множителя слишком малы, то z=0

else

z=(float)minutes/2; //Если 2-й множ-ль нормальный, то

} //вел-на z равна половине времени работы зала.

tau_=MO+z*SKO; // Вычислим нормально распределенное время обсл-я

if( tau_<0 ) // Если время отрицательно, оно равно 1 мин.

tau_=1;

}

else

{

x=RND_DIG(); // Запрос случ. величины от ДСЧ

/* Вычислим равномерно распределенное время обсл-я */

//--------------------------------------------------

tau_=floor( tau_min+x*( tau_max-tau_min )+.5);

}

return floor( tau_+.5 ); //Выведем в место запроса

}

// Ф-я определяет время входа след-го клиента. Промежутки

// между входами распределены по закону Пуассона с пар-м lambda

// ============================================================

float time_to( void )

{

int

j; // Пар-р закона распр-я Пуассона

float

x, // Случ. вел-на

tau, // Время до входа

a, // Пар-р закона распр-я

n, // Половина общего времени работы

S; // Пар-р закона распр-я

n=floor( minutes/2+0.5 );

x=RND_DIG(); // Примем случ. число

tau=0;

j=0;

a=exp( (lambda * (-1)) ); // Расчет нач. знач-я пар-ра а

S=0;

do

{

if( S>=x && xПроверка х на пренадл-ть промежутку [S ; S+a)

break;

tau++;

j++;

S+=a;

a*=lambda/j;

}

while( tau<=n );

return current_time+tau; // Возвратим время до входа след-го клиента

}