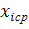
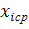
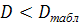
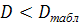
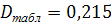
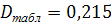
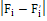
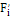
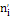
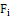
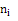
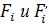
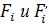
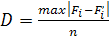
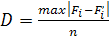
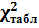
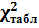
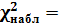
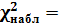
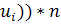
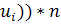
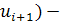
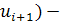
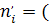
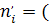
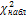
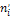
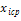
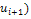
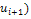
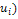
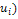
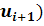
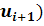
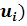
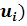
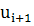
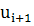
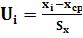
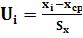
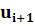
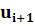
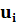
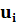
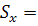
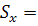
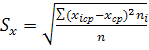
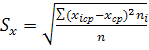
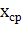
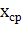
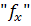
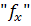
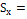
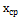
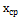
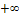
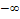
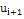
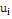
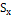
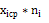
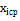
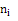
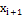
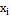
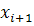
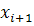
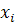
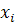
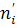
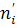
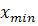
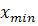
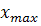
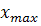
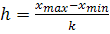
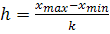
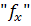
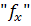
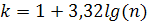
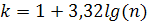
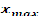
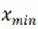
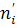
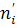
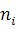
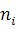
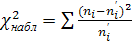
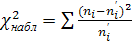5

2

3

1

6

4

8

9

5

7

4

7

8

2

9

10

4

5

3

2

9

7

8

6

5

4

3

5

2

1

2

3

4

1

5

6

7

5

3

10

1. Вычислить критерий хи-квадрат и сделать вывод о нормальности данного распределения.

2. Построить график эмпирического распределения.

Критерий Пирсона

1. Наблюдаемый критерий Пирсона вычисляется по следующей формуле:

критерий пирсон колмогоров распределение частота

,

где - наблюдаемая частота; - теоретическая частота.

Массив данных о значениях случайной величины X, как элементов выборки представим в таблице 1.1 в ячейках В2:К5.

Таблица

A

B

C

D

E

F

G

H

I

J

K

1

2

 

5

2

3

1

6

4

8

9

5

7

3

 

4

7

8

2

9

10

4

5

3

2

4

 

9

7

8

6

5

4

3

5

2

1

5

 

2

3

4

1

5

6

7

5

3

10

6

 

 

 

 

 

 

 

 

 

 

 

7

n=

40

 

k=

6,31884

 

 

 

 

 

 

8

 

10

 

h=

1,42431

 

 

 

 

 

 

9

 

1

 

 

 

 

 

 

 

 

 

2. Разобьем исходные данные по интервалам. Количество интервалов вычислим по формуле , где n – объем выборки.

Объем выборки определим с помощью функции СЧЕТ . Для этого установим курсор в ячейку В7, щелкнем мышкой над кнопкой , которая находится на панели инструментов. Появится окно «Мастер функций – шаг 1 из 2», в котором в категории «Статистические» выбираем функцию СЧЕТ. Затем мышкой выполним команду ОК. В появившемся окне «Аргументы функции» поставим курсор в строку ввода «Значение 1» и мышкой выделим массив В2:К5, щелкнем мышкой ОК. В ячейке В7 появится значение объема данных, число 40.

Введем в ячейку Е7 формулу: =1+3,32*Log(В7),в ячейке Е7 появится число 6,31884.

Далее вычислим шаг интервалов, используя формулу , где - максимальное значение варианты из массива данных; – минимальное значение варианты; k – количество интервалов.

Выделим пустую ячейку В8 и вызовем окно «Мастер функций – шаг 1 из 2», в котором инициируем функцию «МАКС», введем в строку ввода блок ячеек В2:К5. В ячейке В8 появится максимальное значение данных, число 10.Выделим пустую ячейку В9 и вызовем окно «Мастер функций – шаг 1 из 2», в котором инициируем функцию «МИН», введем в строку ввода блок ячеек В2:К5. В ячейке В9 появится максимальное значение данных, число 1.

Теперь введем в ячейку Е8 формулу: =(В8-В9)/Е7. Получим значение шага h=1,42431. Округлим его, получаем h=1,5.

Таким образом, имеем шаг h=1,5, количество интервалов округлим до 7, k=7. Вычислим теоретические частоты по интервалам . Для этого построим новую расчетную таблицу 1.2. Значения частот определяем с использованием функции ЧАСТОТА( ).

Введем в ячейку В11 заголовок для левого конца интервала , в ячейку С11 – заголовок правого конца интервала . Далее вводим значения в столбцы В12:В18 и С12:С18.

Таблица

A

B

C

D

E

F

G

H

I

10

11

12

1

2,5

3

1,75

5,25

59,7417

-1,4232

13

2,5

4

5

3,25

16,25

43,882

-1,4232

-0,8482

14

4

5,5

10

4,75

47,5

21,3891

-0,8482

-0,2731

15

5,5

7

7

6,25

43,75

0,00984

-0,2731

0,30188

16

7

8,5

7

7,75

54,25

16,5473

0,30188

0,8769

17

8,5

10

3

9,25

27,75

27,6792

0,8769

1,45192

18

10

11,5

5

10,75

53,75

102,945

1,45192

19

сумма

40

248,5

272,194

20

=

6,2125

6,80484

21

2,60861

3. 1) Выделим мышкой пустой столбец D12:D18. Щелкнем мышкой над кнопкой функцию ЧАСТОТА. Появится окно «Аргументы и функции». Вводим в строку массив данных блок В2:К5. Затем переводим курсор в строку массив интервалов. Т.е. выделяем столбец В12:В18 и нажимаем последовательно на клавиатуре три кнопки Ctrl+Shift+Enter.

2) Столбец Е12:Е18 заполним средними значениями каждого интервала. В столбце F12:F18 вычислим средние значения для всего массива данных . Для этого в ячейку F12 вводим формулу =D12*E12 и протягиваем мышкой значение этой ячейки до конца таблицы. В ячейке F19 вычисляем сумму, а в ячейке F20 – среднее значение по формуле =F19/D19. =6,2125

3) Вычисляем среднее квадратическое отклонение по формуле

.

Вводим с клавиатуры в ячейку G12 формулу =(E12-59,875)^2*D12 и протягиваем ячейку до ячейки G18. Далее вычисляем в G19 сумму, в ячейке G20 – среднее значение, разделив сумму на 40 и в ячейке G21 извлекаем корень квадратный по формуле =корень(G20). 2,60861.

4. Вычислим безразмерные аргументы для левых концов интервала и для правых концов интервала по формуле .

В ячейку H12 вводим формулу =(В12-6,2125)/ 2,60861 и протягиваем ее до конца столбца, т.е. заполняем нижние значения соответствующими вычислениями. Аналогично вычисляем величины формулой: =(C12-6,2125)/ 2,60861.

Далее вычисляем значения функций Лапласа F( и F( по таблице и результаты помещаем в новую расчетную таблицу 1.3 в ячейки В24:В30 и С24:С30.

Таблица 1.3

A

B

C

D

E

F

22

23

F(

F(

24

-0,5

-0,4222

1,75

3,112

0,00403

25

-0,4222

-0,2968

3,25

5,016

5,1E-05

26

-0,2968

-0,1064

4,75

7,616

0,74625

27

-0,1064

0,1179

6,25

8,972

0,43344

28

0,1179

0,315

7,75

7,884

0,09912

29

0,315

0,4265

9,25

4,46

0,47794

30

0,4265

0,5

10,75

2,94

1,4434

31

сумма

40

3,20423

Вычисляем теоретические частоты по формуле F(F(. Вводим в ячейку E24 формулу =(С24-В24)*60 и протягиваем формулу до конца столбца.

Вычисляем критерий Пирсона Хи-квадрат. В ячейку F24 вводим формулу: =(D12-E24)^2/E24.

В итоге, как видно из таблицы 1.3 получено 3,20423.

Сравним найденное значение с табличным по уровню значимости α=0,05 и степени свободы s=k-2=7-2=5. =11,1

Т.о., наблюдаемый критерий меньше табличного, следовательно, исходные данные соответствуют нормальному закону распределения.

Критерий согласия Колмогорова - Смирнова

Вычислим критерий D по формуле , где – экспериментальные и теоретические накопленные частоты соответственно. Накопленные частоты получаются путем последовательного сложения частот по всем интервалам, начиная с первого. Для удобства вычислений составим расчетную таблицу 2.1.

Таблица 2.1

A

B

C

D

E

F

G

H

I

32

33

3

5

10

7

7

3

5

34

3

8

18

25

32

35

40

35

3,112

5,016

7,616

8,972

7,884

4,46

2,94

36

3,112

8,128

15,744

24,716

32,6

37,06

40

37

0,112

0,128

2,256

0,284

0,6

2,06

 

38

Dmax =

2,256

Максимальное значение абсолютной разности накопленных частот равно 2,256. По формуле делим его на n=40 и получим D=0,0564. Найдем табличное значение критерия с уровнем значимости α=0,05 и степенью свободы n=40. .

Следовательно, исходные данные соответствуют нормальному распределению, т.к. .

Т.о., второй метод подтверждает наличие нормального распределения выборки.

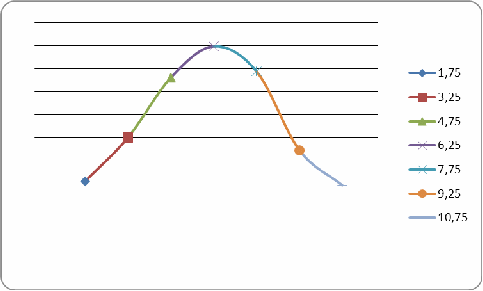
Построение графика распределения частот

Для построения графика распределения частот используем данные таблицы 1.3. В качестве абсциссы берем координаты массив D24:D30. В качестве ординат – блок E24:E30.

1. Выполним команду ВСТАВКА из верхнего меню. Выберем пиктограмму Точечная и в появившемся окне вид плавной кривой с точками.

2. В верхней ленте выбрать команду Выбрать данные. Появится окно Выбор исходных данных. После чего выделяем столбец D24:D30 нажимаем клавишу Ctrl на клавиатуре и, опуская ее, выделяем столбец E24:E30. Щелкнем по команде ОК. Появится изображение графика.

1