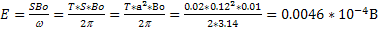
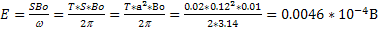
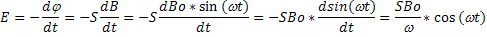
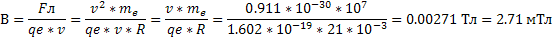
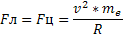
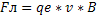
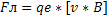
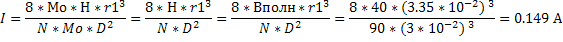
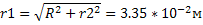
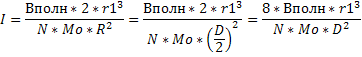
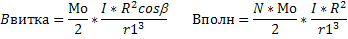
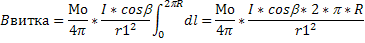
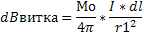
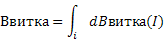
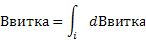
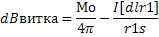
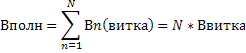
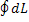
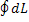
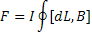
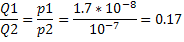
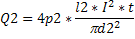
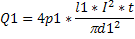
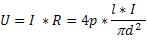
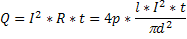
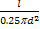
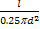
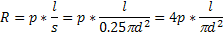
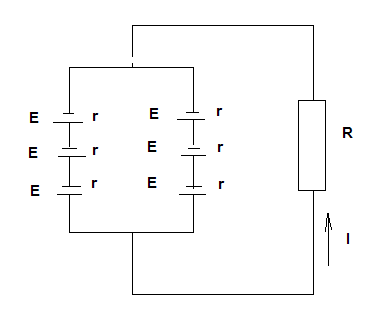
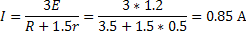
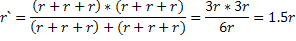
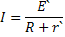
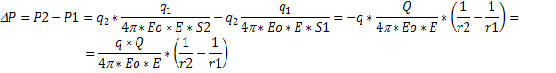
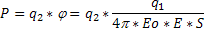
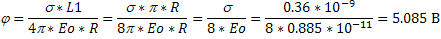
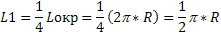
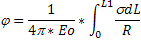
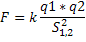
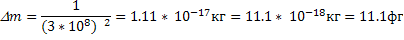
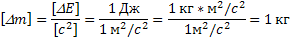
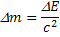
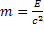
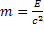
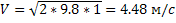
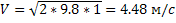
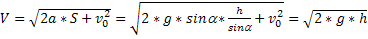
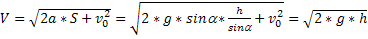
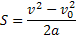
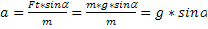
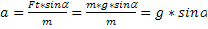
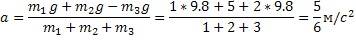
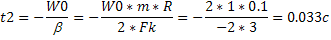
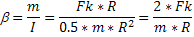
БИЛЕТ № 3

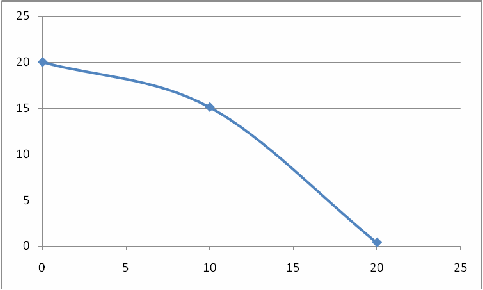
1.Движение материальной точки в поле тяжести земли описывается уравнениями 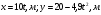. Нарисовать траекторию движения тела .

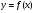РЕШЕНИЕ:

Выразим время через х

T(x)=x/10

Подставим во второе уравнение:

Y(x)=20-4.9*(x/10)²

X 10 20 30 40 0

Y 1.51 0.4 20

2.Диск радиуса 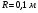вращается относительно оси, проходящей через центр масс, с угловой скоростью 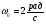. К ободу диска прикладывают касательную тормозящую силу 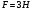. Масса диска 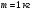. Через какой промежуток времени диск остановится?

РЕШЕНИЕ:

Вычислим угловое ускорение В, создаваемое касательной тормозящей силой Fk. Для чего нам необходимо вычислить момент силы Fk:

М=Fk*R

И момент инерции диска:

I=0.5*m*R²

Тогда выведем ускорение (угловое) :

M=I*

Выразим время до остановки t2:

W2=*t2+W0

3.Определить ускорение тел, связанных нерастяжимой, невесомой нитью, перекинутой через невесомый блок, 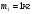, , 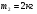, 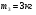внешняя сила 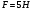. (см.рисунок).

РЕШЕНИЕ:

Рассмотрим силы, действующие на каждое тело, беря за положительное направление – направление движения.

На тело 3:

Т2-F_t3 =m₃a

T2= m₃a+ m₃g= m₃(a+g)

На тело 2:

F_t2 +T1-T2= m₂a

m₂g+T1-T2= m₂a

T1= m₂(a-g)+ m₃(a+g)

На тело 1:

F_t1+F-T1= m₁a

m₃a+F-T1= m₁a

m₁a+F- m₂a+ m₂g- m₃a- m₃g= m₁a

m₁a+ m₂a+ m₃a= m₁a+F+ m₂g+ m₃g

4.

m₃

m₂

m₁

F

F

Тело массой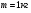 соскальзывает без трения с наклонной плоскости, имеющей высоту 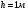. Какую скорость будет иметь тело у подножия наклонной плоскости?

РЕШЕНИЕ:

Так как м₀=0, то на оси ОХ на тело действует лишь проекция силы F_Т на ось ОХ.

m_a=F_T*sin

a=

Путь S пройденный телом до конца наклонной плоскости:

S=h/sin

Зная выражение пути равноускоренного движения:

Выразим V:

так как V₀=0

5.Полная энергия тела возросла на 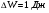. На сколько при этом изменилась его масса?

РЕШЕНИЕ:

Согласно теории относительности полная энергия тела определяется выражением:

E=m*c² (1)

Где m – релятивистская масса тела, с – скорость света в вакууме (с=3*10⁸ м/c)

Из выражения (1) получаем:

(2)

При увеличении полной энергии тела на Е масса тела, согласно (2), возрастает на величину:

Проверим размерность:

Подставим численные значения и произведем вычисления:

6.

+q₃

-q₂

+q₁

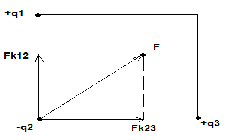
Одинаковые по величине заряды q₁, q₂ и q₃ находятся в трех вершинах квадрата. Как направлена сила, действующая на заряд q₂ со стороны двух других зарядов? Ответ обосновать.

РЕШЕНИЕ:

Из закона Кулона следует, что разноименные заряды притягиваются. Следовательно F_R1,2, действующая со стороны первого заряда на второй заряд, направлена по линии, соединяющей эти два заряда от второго к первому. Аналогично и сила F_R2,3 направлена от второго к третьему. Так как заряды q1=q3 и расстояния Sq1q2=Sq2q3,

то по закону Кулона следует, что F_R1,2 по модулю равна F_R2,3

Используя принцип суперпозиции сил проведем векторное сложение F_R1,2 и F_R2,3

F= F_R1,2 + F_R2,3

Таким образом, сила F будет направлена по диагонали квадрата, как показано на рисунке.

7.Незаряженное металлическое тело М, смотри рисунок, внесли в электрическое поле положительного заряда 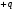, а затем разделили на две части и 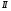. Каким зарядом обладают части тела и 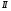после их разделения?

РЕШЕНИЕ:

После внесения незаряженного металлического тела М в электрическое поле положительного заряда q, в зону I согласно закону Кулона начнут притягиваться свободные отрицательно заряженные частицы тела М (электроны), а в зону II – положительно заряженные частицы (условно «дырки»). Таким образом после разделения тела М в его I части скопится отрицательный заряд, равный по модулю положительному заряду, скопившемуся в части II.

8.Электростатическое поле создается равномерно заряженной бесконечной плоскостью. Покажите, что это поле является однородным.

РЕШЕНИЕ:

Пусть поверхностная плотность заряда равна . Очевидно что вектор Е может быть только перпендикулярным заряженной плоскости. Кроме того очевидно, что в симметричных относительно этой плоскости точках вектор Е одинаков по модулю и противоположен по направлению. Такая конфигурация поля подсказывает, что в качестве замкнутой поверхности следует выбрать прямой цилиндр, где предполагается что  больше нуля. Поток сквозь боковую поверхность этого цилиндра равен нулю, и поэтому полный поток через всю поверхность цилиндра будет равным 2*Е*S, где S – площадь каждого торца. Согласно теореме Гаусса

2*Е*S=*S,

где *S – заряд заключенный внутри цилиндра.

Откуда

Е=/2*Ео.

Точнее это выражение следует записать так:

Еn=/2*Eo,

где Еn – проекция вектора Е на нормаль n к заряженной плоскости, причем вектор n направлен от этой плоскости.

Тот факт, что Е не зависит от расстояния до плоскости, означает, что соответствующее электрическое поле является однородным.

9.Из медной проволоки изготовлена четверть окружности радиусом 56 см. По проволоке равномерно распределен заряд с линейной плотностью 0,36 нКл/м. Найдите потенциал в центре окружности.

РЕШЕНИЕ:

Так как заряд линейно распределен по проволоке для нахождения потенциала в центре воспользуемся формулой:

Где  - линейная плотность заряда, dL – элемент проволоки.

10.В электрическом поле, созданном точечным зарядом Q, по силовой линии из точки расположенной на расстоянии r₁ от заряда Q в точку, расположенную на расстоянии r₂, перемещается отрицательный заряд -q. Найдите приращение потенциальной энергии заряда -q на этом перемещении.

РЕШЕНИЕ:

По определению потенциал – это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля. Следовательно потенциальная энергия заряда q₂:

Отсюда

11.Два одинаковых элемента с э.д.с. 1,2 В и внутренним сопротивлением 0,5 Ом соединены параллельно. Полученная батарея замкнута на внешнее сопротивление 3,5 Ом. Найдите силу тока во внешней цепи.

РЕШЕНИЕ:

Согласно закону Ома для всей цепи сила тока во внешней цепи:

Где E` - ЭДС батареи элементов,

r` - внутреннее сопротивление батареи, которое равно:

ЭДС батареи равна сумме ЭДС трех последовательно соединенных элементов:

E`=E+E+E=3E

Следовательно:

12 В электрическую цепь включены последовательно медная и стальная проволоки равной длины и диаметра. Найдите отношение количеств тепла выделяющегося в этих проволоках.

РЕШЕНИЕ:

Рассмотрим проволоку длиной L и диаметром d, изготовленную из материала с удельным сопротивление p. Сопротивление проволоки R можно найти по формуле

Где s= – площадь поперечного сечения проволоки. При силе тока I за время t в проводнике выделяется количество теплоты Q:

При этом, падение напряжения на проволоке равно:

Удельное сопротивление меди:

p1=0.017 мкОм*м=1.7*10^-8Ом*м

удельное сопротивление стали:

p2=10^-7Ом*м

так как проволоки включены последовательно, то силы тока в них одинаковы и за время t в них выделяются количества теплоты Q1 и Q2:

Отсюда:

12.В однородном магнитном поле находится круговой виток с током. Плоскость витка перпендикулярна силовым линиям поля. Докажите, что результирующая сил, действующих со стороны магнитного поля на контур, равна нулю.

РЕШЕНИЕ:

Так как круговой виток с током находится в однородном магнитном поле, на него действует сила Ампера. В соответствии с формулой dF=I[dL,B] результирующая амперова сила, действующая на виток с током определяется:

Где интегрирование проводится по данному контуру с током I. Так как магнитное поле однородно, то вектор В можно вынести из-под интеграла и задача сволится к вычислению векторного интеграла . Этот интеграл представляет замкнутую цепочку элементарных векторов dL, поэтому он равен нулю. Значит и F=0, то есть результирующая амперова сила равна нулю в однородном магнитном поле.

13.По короткой катушке, содержащей 90 витков диаметром 3 см, идет ток. Напряженность магнитного поля, созданного током на оси катушки на расстоянии 3 см от нее равна 40 А/м. Определите силу тока в катушке.

РЕШЕНИЕ:

Считая, что магнитная индукция в точке А есть суперпозиция магнитных индукций, создаваемых каждым витком катушки в отдельности:

Для нахождения В_витка воспользуемся законом Био-Савара-Лапласа.

Где, dBвитка – магнитная индукция поля, создаваемая элементом тока IDL в точке, определяемой радиус-вектором r Выделим на конце элемент dL и от него в точку А проведем радиус-вектор r. Вектор dBвитка направим в соответствие с правилом буравчика.

Согласно принципу суперпозиции:

Где интегрирование ведется по всем элементам dLвитка. Разложим dBвитка на две составляющие dBвитка(II) – параллельную плоскости кольца и dBвитка(I) – перпендикулярную плоскости кольца. Тогда

Заметив, что из соображений симметрии и что векторы dBвитка(I) сонаправленные, заменим векторное интегрирование скалярным:

Где dBвитка(I) =dBвитка*cos и

Поскольку dl перпендикулярен r

Сократим на 2 и заменим cos на R/r1

Выразим отсюда I зная что R=D/2

согласно формуле связывающей магнитную индукцию и напряженность магнитного поля:

В=Мо*Н,

тогда по теореме Пифагора из чертежа:

14.В однородное магнитное поле в направлении перпендикулярном силовым линиям влетает электрон со скоростью 10۰10⁶ м/с и движется по дуге окружности радиусом 2,1 см. Найдите индукцию магнитного поля.

РЕШЕНИЕ:

На электрон, движущийся в однородном магнитном поле будет действовать сила Лоренца, перпендикулярная скорости электрона и следовательно направленная к центру окружности:

Так как угол между v и И равен 90⁰:

Так как сила Fл направлена к центру окружности, и электрон двигается по окружности под действием этой силы, то

Выразим магнитную индукцию:

15. Квадратная рамка со стороной 12 см, изготовленная из медной проволоки, помещена в магнитное поле, магнитная индукция которого меняется по закону В=В₀·Sin(ωt), где В₀=0,01 Тл, ω=2·π/Т и Т=0,02 с. Плоскость рамки перпендикулярна к направлению магнитного поля. Найдите наибольшее значение э.д.с. индукции, возникающей в рамке.

РЕШЕНИЕ:

Площадь квадратной рамки S=a². Изменение магнитного потока d, при перпендикулярности плоскости рамки d=SdB

ЭДС индукции определяется

Е будет максимальна при cos(t)=1

=0.46 мк В