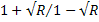
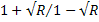
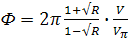
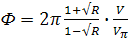
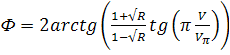
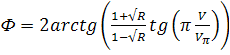
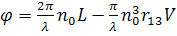
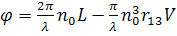
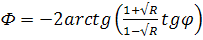
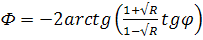
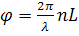
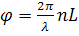
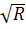
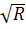
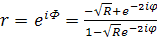
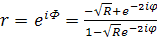
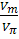
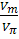
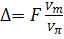
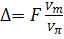
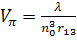
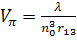
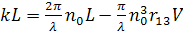
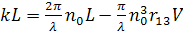
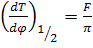
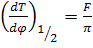
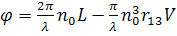
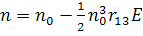
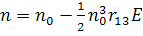
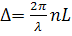
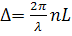
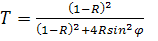
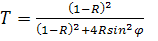
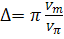
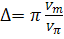
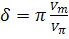
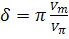
Федеральное агентство по образованию

ФГОУ ВПО "СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ"

Инженерно физическое отделение

Институт инженерной физики и радиоэлектроники

Кафедра экспериментальной и медицинской физики

Реферат:

Электрооптические модуляторы света

Проверил: д. ф. - м. н.А.Н. Втюрин

Выполнил:

студент Н.А. Шпак

Красноярск 2009

Введение

Электрооптическая модуляция позволяет управлять лазерным пучком или контролировать сигнал излучения с высокой скоростью (вплоть до частоты в несколько гигагерц), поскольку при этом не используется механическое перемещение элементов.

Принцип действия основан на изменении эллипсоида показателей преломления под действием внешнего электрического поля. При распространении линейно-поляризованных нормальных мод через пластинку показатель преломления будет зависеть от напряженности поля. Очевидно, что фазовый сдвиг этих нормальных мод при прохождении через кристалл зависит от показателя преломления. После прохождения в кристалле расстояния L волна претерпевает следующий фазовый сдвиг благодаря наложенному электрическому полю:

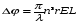₍1)

где λ - длина волны света, n - показатель преломления, r - соответствующий электрооптический коэффициент, а Е - напряженность приложенного электрического поля. Если Е изменяется во времени синусоидально, то фазовая задержка волны следует за изменением приложенного электрического поля и также изменяется синусоидально, если только частота модуляции не слишком высока. Таким образом, электрооптический эффект непосредственно приводит к фазовой модуляции этих нормальных мод. Амплитудную модуляцию можно получить, комбинируя две распространяющиеся нормальные моды и два различных индуцированных электрооптических фазовых сдвига. Обычно для создания фазовой задержки линейно-поляризованного света необходимо иметь всего один поляризатор. Для амплитудной же модуляции требуется дополнительный поляризатор (анализатор), ориентированный под определенным углом для получения соответствующей интерференции. Электрооптическая модуляция световых волн также подразделяется на два основных типа в зависимости от направления приложенного электрического поля. Если электрическое поле параллельно направлению распространения, то модуляция называется продольной. Если же электрическое поле перпендикулярно направлению распространения, то модуляцию называют поперечной. Рассмотрим ниже оба этих случая по отдельности.

Продольная электрооптическая модуляция

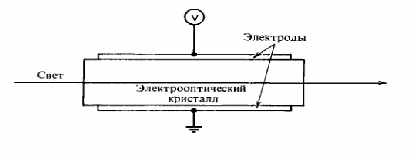
На рис.1 изображена геометрия продольного электрооптического модулятора. Этот модулятор представляет собой тонкую электрооптическую кристаллическую пластинку большой площади.

Вектор модулирующего электрического поля параллелен направлению распространения света всюду, кроме области электродов. В случае линейного электрооптического эффекта изменение показателя преломления, вызванное электрическим полем, пропорционально напряженности электрического поля Е. Вызванное электрическим полем изменение фазы (фазовая задержка) для света, проходящего через кристаллическую пластинку, пропорционально величине EL, которая равна приложенному напряжению V и не зависит от толщины кристаллической пластинки L.

Рис.1. Геометрия типичного продольного электрооптического модулятора.

Величина глубины модуляции пропорциональна приложенному напряжению. Полуволновые напряжения прямо пропорциональны длине волны света и обратно пропорциональны электрооптическому коэффициенту. Для света в видимом диапазоне длин волн эти напряжения имеют величину порядка нескольких киловатт. Увеличение толщины пластинки приводит к увеличению длины взаимодействия, но и к уменьшению напряженности электрического поля. Следовательно, полное увеличение модуляции за счет увеличения толщины пластинки при продольной модуляции отсутствует. Для излучения ИК-диапазона из-за большой длины волны света (скажем, 10,6 мкм) возникает необходимость в приложении высоких напряжений. Продольные модуляторы используются только тогда, когда требуются большие площади устройства и большое поле зрения.

Поперечная электрооптическая модуляция

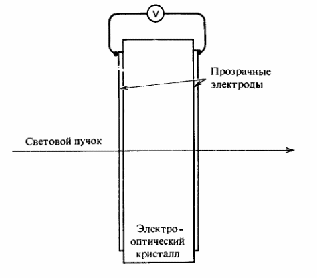
Геометрия поперечного электрооптического модулятора приведена на рис.2. При данной напряженности электрического поля такая структура позволяет обеспечить большую длину взаимодействия. Модулирующее поле является поперечным относительно направления распространения оптического пучка. Ограничиваясь рассмотрением только линейных электрооптических эффектов, можно показать, что изменение показателя преломления, индуцированное электрическим полем, пропорционально напряженности поля Е. Электрически индуцированное изменение фазы (или фазовая задержка) для света, проходящего через кристаллическую пластинку, пропорционально при этом величине EL, или VL/d, где d - расстояние между электродами. Таким образом, изменение фазы пропорционально длине кристалла L. Это преимущество было использовано при создании электрооптических модуляторов лазерных пучков с низкими управляющими напряжениями.

Рис.2. Геометрия типичного поперечного электрооптического модулятора.

Электрооптические модуляторы Фабри-Перо

Выше при рассмотрении электрооптических модуляторов, в частности с поперечной геометрией (рис.2), было показано, что модуляция пропорциональна длине взаимодействия L. Если V_m - амплитуда модулирующего напряжения и на модулятор подано соответствующее смещающее напряжение, то глубину фазовой модуляции можно записать в виде

(2)

а глубина амплитудной модуляции принимает вид:

(3)

Согласно (2) и (3), для осуществления большой глубины модуляции полуволновые напряжения должны быть малы при данном напряжении модуляции, а для этого в случае поперечной схемы модулятора требуются кристаллы большой длины. Так как в оптическом резонаторе свет отражается многократно, эффективная длина взаимодействия светового пучка в электрооптическом кристалле сильно возрастает. Это существенно увеличивает глубину модуляции как в фазовых, так и в амплитудных модуляторах. Рассмотрим теперь эти устройства более подробно.

Амплитудная модуляция

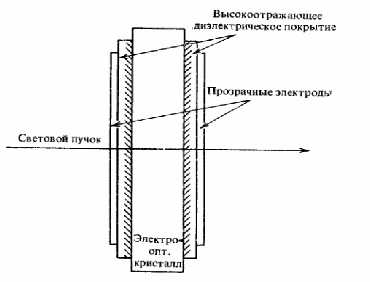
Рассмотрим тонкую пластинку, представляющую собой z-срез кристалла LiNbO₃, помещенную между диэлектрическими зеркалами с большой эффективностью отражения (рис.3). На внешнюю поверхность общей структуры наложены прозрачные электроды. Коэффициент пропускания резонатора Фабри-Перо дается выражением

(4)

где R - коэффициент отражения зеркал, а φ - фазовый сдвиг света при прохождении через среду, определяемый следующим образом:

(5)

здесь L - толщина пластинки. Показатель преломления n при наличии внешнего электрического поля записывается в виде

(6)

Рис.3. Электрооптический модулятор Фабри-Перо.

Подставляя выражение (6) для n в (5), получаем

(7)

где V - приложенное напряжение.

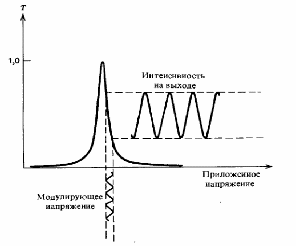
Рис.4. Зависимость коэффициента пропускания электрооптического модулятора Фабри-Перо от приложенного напряжения.

Модулятор смещен в рабочую точку, расположенную на полувысоте максимума пропускания. Небольшое приложенное синусоидальное напряжение приводит к модуляции интенсивности на выходе относительно точки смещения. Если падающий световой пучок является монохроматическим, то интенсивность прошедшего пучка зависит от величины φ, которая, как следует из (7), является электрически перестраиваемой. Кроме того, если резонатор Фабри-Перо смещен таким образом, что коэффициент его пропускания в отсутствие модулирующего напряжения равен 50%, то интенсивность прошедшего излучения будет сильно модулироваться относительно малыми модулирующими напряжениями. Это иллюстрируется на рис.4. Большая глубина модуляции обусловлена резким пиком пропускания, разумеется, при условии, что резонатор имеет высокую добротность. Действительно, в соответствии с выражением (4) наклон кривой пропускания в точке, расположенной на ее полувысоте, запишется в виде

(8)

где F - добротность резонатора. Нетрудно изготовить резонаторы Фабри-Перо с добротностью F = 30. Таким образом, наклон кривой пропускания, определяемый выражением (8), может быть порядка 10. В обычных амплитудных модуляторах этот наклон равен 1. Пусть приложенное напряжение имеет вид V = V_msinω_mt.

Световой пучок, прошедший через модулятор, приобретает фазовый множитель е^-ikL, который содержит фазу, отвечающую нулевому полю (Е = 0), и электрически индуцированное изменение фазы вычисляется по формуле:

(9)

где V - приложенное напряжение. Напряжение, требуемое для изменения фазы на π, называется полуволновым напряжением фазовой модуляции и дается выражением

(10)

Тогда глубину модуляции прошедшего пучка с помощью выражений (8), (9) и (10) можно записать в виде

(11)

Заметим, что по сравнению с выражением (3) здесь при том же напряжении глубина модуляции увеличивается в F/π раз.

Фазовая модуляция

Хотя амплитудно-модулированный свет после прохождения через электрооптический модулятор Фабри-Перо оказывается промодулированным также и по фазе, имеется необходимость в получении светового пучка с чисто фазовой модуляцией.

Рис.5. Работа асимметричного реюнатора Фабри - Перо (эталона Жира-Турнуа) в качестве фазового модулятора.

Идеализированная структура чисто фазового модулятора изображена на рис.5.

Он представляет собой асимметричный резонатор Фабри-Перо, заднее зеркало которого имеет коэффициент отражения 100%. Переднее зеркало имеет частично отражающее диэлектрическое покрытие с R < 1,0. Это так называемый эталон Жира-Турнуа.

Коэффициент отражения полной структуры, очевидно, равен 100%, поскольку свет не может проходить через второе зеркало и полная структура не имеет потерь.

Если в спектральном диапазоне, представляющем интерес, коэффициент отражения зеркала сохраняется равным 100%, то будет отражаться вся электромагнитная энергия. Действительно, коэффициент отражения можно записать в виде

(12)

где мы положили

r₁₂ = - , г₂₃ = 1, а φ дается выражением

(13)

Фазовый сдвиг Ф после отражения определяется выражением (12) и может быть выражен через φ следующим образом:

(14)

В предельном случае, когда коэффициент отражения переднего зеркала равен нулю (R = 0), мы имеем Ф = - 2φ, т.е. фазовый сдвиг совпадает с полным оптическим фазовым сдвигом светового пучка, прошедшего через резонатор в прямом и обратном направлениях. Если коэффициент отражения больше нуля (R>0), то в асимметричном резонаторе Фабри-Перо фазовый сдвиг Ф существенно возрастает из-за многократных отражений (см. рис.5). Для пластинки, представляющей собой z-срез кристалла LiNbO₃, фазовый сдвиг φ при наличии электрического поля дается выражением (7):

(7)

Кроме того, если к электрооптическому кристаллу приложено соответствующее смещающее напряжение, то в отсутствие модулирующего напряжения мы имеем φ = m_π. Таким образом, фазовый сдвиг Ф отраженного пучка можно записать в виде

(15)

Предположим теперь, что модулирующее напряжение мало, так что глубина фазовой модуляции

(16)

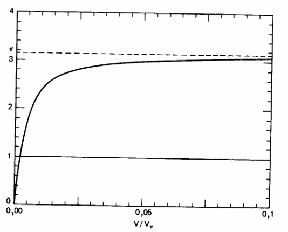
Заметим, что наличие переднего зеркала увеличивает глубину модуляции в раз. Например, при R = 0,9 глубина фазовой модуляции увеличивается в 38 раз. На Рис.6 представлена зависимость Ф от V/V_m. Выражение (16) является линейной аппроксимацией зависимости (15).

Приведенные два примера продемонстрировали, что оптическая обратная связь, создаваемая резонатором Фабри-Перо, значительно увеличивает длину взаимодействия и, следовательно, глубину модуляции при данной величине напряжения. Однако это увеличение возможно лишь для тех оптических частот, которые удовлетворяют условиям резонанса Фабри-Перо. Иными словами, к электрооптическому кристаллу необходимо приложить соответствующее смещающее напряжение.

Рис.6. Зависимость Ф от V при R = 0,95.

Поскольку фазовое смещение зависит от длины волны, на других длинах волн резонатор нельзя сместить в нужную рабочую точку. Следовательно, присутствие оптического резонатора уменьшает полосу пропускания модулятора на оптических частотах.