Физические основы явления выстрела
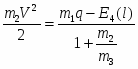
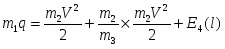
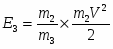
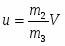
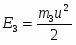
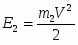
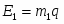
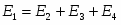
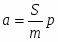
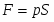
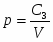
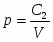
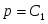
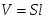
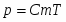
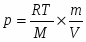
 Физические основы явления выстрела
Физические основы явления выстрела
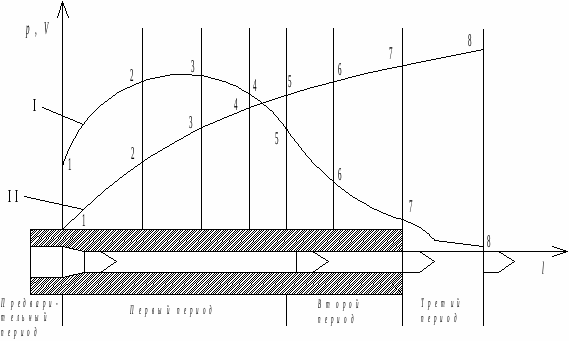
В некотором приближении поведение пороховых газов можно описать с помощью уравнения Менделеева Клапейрона. Это позволяет качественно проанализировать явление выстрела и построить графики зависимости давления газа p скорости пули v от пути l, проходимого ею в канале ствола (см. Рис.).
Рассмотрим, как происходит процесс выстрела. Его длительность можно условно разделить на такие последовательные периоды: предварительный от начала горения порохового заряда до полного врезания оболочки пули в нарезы ствола; первый от начала движения пули по стволу до полного сгорания порохового заряда; второй от момента полного сгорания порохового заряда до момента вылета пули из ствола; третий от момента вылета пули до прекращения возрастания её скорости.
Рассмотрим, как меняется давление порохового газа при выстреле (кривая I на рис.).
Предварительный период. Во время горения заряда образуется пороховой газ. Давление его можно выразить формулой:
(1)
где Т, V и m соответственно температура, объём и масса порохового газа, М его молярная масса, R универсальная газовая постоянная. Поскольку объём газа не меняется, а температура и масс резко увеличиваются, давление газа будет расти по закону:
,
где С постоянная величина. Давление пороховых газов будет возрастать до тех пор, пока пуля не сдвинется с места.
Первый период. Его условно можно разделить на три полпериода. Рассмотрим их поочерёдно.
Масса порохового газа m возрастает быстрее, чем объём V запульного пространства (объём, заключённый между дном пули и дном гильзы). Учитывая, что
(S площадь сечения канала ствола, l путь пули в канале ствола), изменение давления газа в первый подпериод можно представить графически в виде участка 1-2 кривой I.
Скорость возрастания массы порохового газа становится близкой к скорости движения пули, или, что одно и то же, к скорости изменения объёма V. Тогда формула (1) принимает вид
,
где С1 постоянная величина. Графически изменение давления в этот подпериод можно представить в виде участка 3-4 кривой I.
Объём V запульного пространства вследствие быстрого увеличения скорости пули растёт гораздо быстрее массы m притока порохового газа, и изменением массы можно пренебречь. Тогда формула (1) примет вид:
,
где С2 постоянная величина. Изменение давления газа в этот подпериод можно представить в виде участка 5-6 кривой I.
Промежуточные процессы между подпериодами можно приближённо изобразить соответствующими участками 2-3 и 4-5 кривой I.
Второй период. Так как весь пороховой заряд уже сгорел, масса газа не меняется. Тогда формула (1) принимает вид
,
где С3 постоянная величина. Изменение давления можно представить участком 6-7 кривой I.
Третий период. Часть газа вырывается из канала ствола вслед за пулей, при встрече с воздухом образует пламя и ударную волну. Следовательно, масса газа m уменьшается. Так как при этом увеличивается объём газа, то, согласно формуле (1), происходит резкое падение давления газа (участок 7-8 кривой I). Это уменьшение происходит до тех пор, пока давление порохового газа на дно пули не уравновесится сопротивлением воздуха.
График изменения скорости пули в канале ствола (кривая II на рис.) можно построить, если предположить, что сила, действующая на пулю со стороны пороховых газов, много больше силы сопротивления, силы трения и т. д.
В предварительный период скорость пули не меняется. В остальные периоды ускорение пули пропорционально давлению. Действительно, на пулю действует сила:
,
где p давление порохового газа, S площадь сечения канала ствола. Следовательно, если масса пули m, то её ускорение
.
Поскольку давление газа в канале ствола во все периоды много больше атмосферного, ускорение пули будет больше нуля, т. е. Она будет двигаться ускоренно.
В первый подпериод ускорение увеличивается, следовательно, скорость пули будет резко возрастать. Графически это изменение скорости можно представить в виде участка 1-2 кривой II. Во второй подпериод ускорение почти не изменяется, поэтому движение пули будет близким к равноускоренному (участок 3-4 кривой II). В третий подпериод ускорение пули уменьшается, но остаётся положительным, следовательно, прирост скорости пули уменьшается (участок 5-6 кривой II). Во второй и третий периоды происходит дальнейшее уменьшение ускорения, что соответствует уменьшению прироста скорости (участок 7-8 кривой II).
Можно исследовать начальную скорость пули с помощью законов сохранения. Начальной скоростью пули называется та скорость, с которой она покидает канал ствола. Закон сохранения энергии для явления выстрела можно записать так:
. (2)
Здесь Е1 энергия, выделяющаяся при сгорании пороха, Е2 кинетическая энергия пули в момент вылета из канала ствола, Е3 кинетическая энергия стрелкового оружия, Е4 энергия, уносимая выброшенными пороховыми газами, идущая на нагревание ствола, и т. д.
Очевидно,
(3)
(q теплота сгорания пороха, m1 его масса);
(4)
(m2 масса пули, V её скорость в момент вылета из ствола);
(5)
(m3 масса оружия, u скорость отдачи при выстреле), причём, поскольку согласно закону сохранения импульса,
,
выражение (5) можно записать в виде:
. (6)
Энергия Е4 зависит прежде всего от длины ствола l. При малой длине много энергии будет выбрасываться наружу, при слишком большой окажутся значительными потери энергии на нагревание ствола и преодоление сил сопротивления, действующих на пулю в его канале. Следовательно, важно выбрать некоторую оптимальную длину ствола, при которой энергия Е4 будет минимальной.
Учитывая (3)-(6) и приведённые выше рассуждения, выражение (2) можно переписать в виде:
.
Откуда начальная кинетическая энергия пули:
.
С помощью этой формулы легко доказать следующие утверждения:
начальная скорость пули зависит от длины ствола, массы пули, массы порохового заряда и от других факторов;
чем длиннее ствол (до известных пределов), тем дольше действует на пулю пороховой газ и тем больше её начальная скорость;
при постоянных длине ствола и массе порохового заряда начальная скорость пули тем больше, чем меньше её масса.
Можно сказать, что скорость пули зависит и от массы стрелкового оружия.

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ