Цель работы: исследовать АЧХ и ФЧХ последовательного и параллельного колебательного контура, определить резонансную частоту, найти добротность последовательного контура.

Приборы и материалы: колебательный контур, осциллограф, источник питания, генератор, провода, магазин сопротивлений, индуктивностей и конденсаторов.

Теоретическая часть

Колебательным контуром называют электрическую цепь, состоящую из элементов, способных запасать электрическую и магнитную энергию, и в которой могут возбуждаться электрические колебания. Эквивалентная схема простейшего колебательного контура состоит из ёмкости, индуктивности и сопротивления.

Колебательные контуры нашли широчайшее применение в радиоэлектронике в качестве различных частотно- избирательных систем, то есть, систем, у которых амплитуда отклика цепи может резко изменится, когда частота внешнего воздействия достигает некоторых значений, определяемых параметрами цепи. Явление резкого возрастания амплитуды отклика называется амплитудным резонансом.

В теории цепей обычно используется другое определение резонанса. Под резонансом понимают такой режим работы электрической цепи, содержащей ёмкости и индуктивности, при котором реактивные составляющие входных сопротивления и проводимости равны нулю, то есть, отсутствует сдвиг фаз между напряжением и током на входе колебательного контура. Такой резонанс называют фазовым. Частоты, соответствующие фазовому и амплитудному резонансам, как правило, близки и в некоторых случаях могут совпадать.

Простейшей электрической цепью, в которой наблюдается явление резонанса, является одиночный колебательный контур, состоящий из катушки индуктивности и конденсатора, соединённых в замкнутую цепь. В зависимости от способа подключения к колебательному контуру источника энергии различают последовательный (рис.1) и параллельный (рис.2) колебательные контура.

График АЧХ для последовательного контура приведён на рис.3. Из графика видно, что графики АЧХ для C и L пересекаются при резонансной частоте 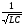 = . Найдём частоты, при которых АЧХ достигает максимума. Они равны

= (1)

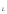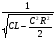= (2)

ω_p

f

1

2

3

4

5

K

• для R,

• для C,

• для L.

рис.3.

Графики ФЧХ выглядят следующим образом

f

-1.5

-1

-0.5

0.5

1

1.5



рис.4

- для R

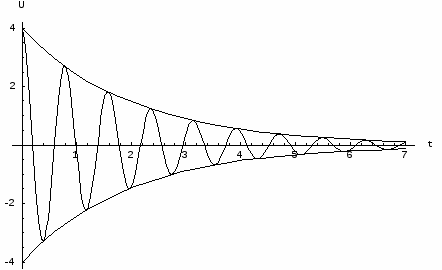
При подаче импульсного напряжения мы получим график затухающих колебаний (рис.5), в аналитическом представлении этот график имеет вид

U(t) = U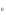ecost (3)

где  - коэффициент затухания.

рис.5.

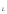Кроме  у системы есть ещё одна важная характеристика Q – добротность, которую можно найти как отношение U или U к U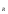 при резонансной частоте. Через параметры системы выражениe для Q можно записать в виде

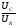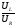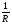
Q = = = 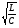(4)

Так же добротность можно выразить через ,т.е.

Q = 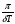(5)

где T – период колебания.

Практическая часть

Задание 1: Исследовать амплитудно-частотные характеристики последовательного колебательного контура. Определить добротность. Построить графики.

1). Для индуктивности (С = 10000 пФ; R = 62 Ом; L=2,6 мГн)

Таблица 1: Зависимость коэффициента усиления от частоты.

f,кГц

2

5

8

10

13

15

18

20

21

23

25

28

32

35

36

39

K

0,2

1,2

2,7

3,9

4,5

5,1

6,3

8,7

9,9

13

16

20

16

10

6,1

2,1

2). Для конденсатора (С = 10000 пФ; R = 62 Ом; L=2,6мГн)

Таблица 2: Зависимость коэффициента усиления от частоты.

f,кГц

10

14

16

20

24

26

27

28

30

35

40

50

60

80

100

K

1,2

1,4

1,6

2,5

4,7

8,4

21,7

16,6

7,8

3,4

1,9

0,7

0,6

0,2

0,1

3).Для сопротивления (С = 10000 пФ; R = 62 Ом; L=2,6 мГн )

Таблица 3: Зависимость коэффициента усиления и разности фаз от частоты

f,кГц

6

8

9

10

12

14

16

19

K

0,03

0,05

0,06

0,09

0,12

0,14

0,15

0,18

,^

66,6

59,4

55,8

54

52,2

45

43,2

36

f,кГц

25

26

27

28

30

33

35

K

0,57

0,91

0,79

0,66

0,52

0,41

0,28

,^

23,4

10,8

16,2

25,2

109,8

118,8

126

График 1. АЧХ для L,С

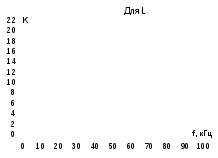
График 2. АЧХ для сопротивления

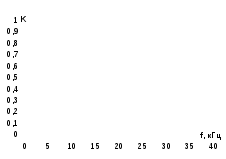
График 3. ФЧХ для сопротивления

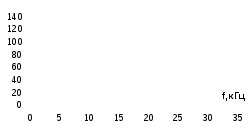
Из графика 1 видно, что резонансная частота f_р, = 26 кГц.

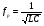
Определение добротности последовательного контура:

(С = 10 000 пФ; R = 62 Ом; L=2,6 мГн).

Добротность рассчитаем двумя способами:

1-ый способ: используя параметры контура:

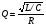
Получаем, что Q = 8,14

2-ой способ: по полученной АЧХ контура:

Q= f₀/f_0,7

Получаем, что Q = 13,73

Задание 2: Исследовать амплитудно-частотную (АЧХ) и фазово-частотную (ФЧХ) характеристики параллельного колебательного контура. Определить период затухания при подаче сигнала с импульсного генератора. Построить графики.

Параллельный контур. (С = 10000 пФ; R = 1 кОм; L=2,6 мГн )

Таблица 4:Зависимость коэффициента усиления и разности фаз от частоты.

f,кГц

1,2

2

3

5

7

10

14

18

K

0,02

0,04

0,07

0,12

0,15

0,20

0,31

0,62

,^

77,4

55,8

54

45

46,8

36

32,4

32,4

f,кГц

23

25

29

30

35

40

50

K

0,95

0,87

0,77

0,64

0,51

0,47

0,33

,^

14,4

21,6

30,6

18

18

18

18

Графики представлены ниже

График 4. АЧХ параллельного контура

График 5. ФЧХ для параллельного контура

По полученным данным можно определить резонансную частоту.

f_p = 23 кГц.

Определение добротности параллельного контура:

(С = 10 000 пФ; R = 1 кОм; L=2,6 мГн).

Снова рассчитаем добротность Q двумя способами:

1-ый способ:

Q=f₀/f_0,7= 1,92

2-ой способ:

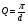= 2,35

Выводы:

1. Был исследован последовательный колебательный контур, получены амплитудно-частотные и фазово-частотные характеристики, определена резонансная частота, равная 26 кГц. Расхождения с теорией лежат в пределах допустимой погрешности. Графики, полученные в ходе работы, совпадают с ожидаемым результатом.

2. Исследован параллельный колебательный контур. Для него также были построены АЧХ и ФЧХ. Определена резонансная частота f_p = 23 кГц.

3. Исследован и зарисован отклик последовательного и параллельного контуров на импульсное воздействие. По полученному графику определен период затухания контура при данных параметрах Т = 18*10^-6 с.

4. По полученным данным определены добротности последовательного и параллельного контура. Различия между значениями добротностей были объяснены выше.

Литература:

1. В.Н. Ушаков. ”Основы радиоэлектроники и радиотехнические устройства”. М., «Высшая школа», 1976.

2. Е.И. Манаев. “Основы радиоэлектроники”. М., «Радио и связь», 1985.

3. П.Н.Урман, М.А. Фаддеев: ”Расчет погрешностей экспериментальных результатов”.