1

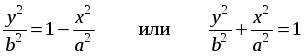
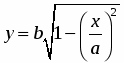
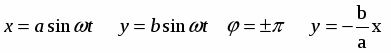
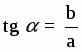
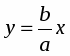
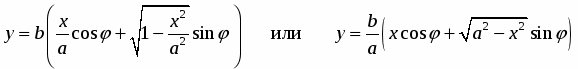
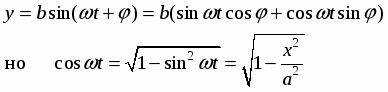
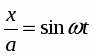
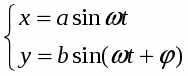
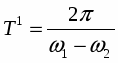
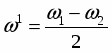
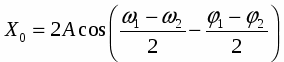
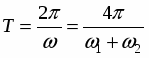
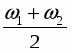
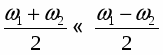
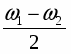
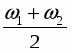
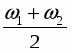
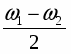
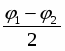
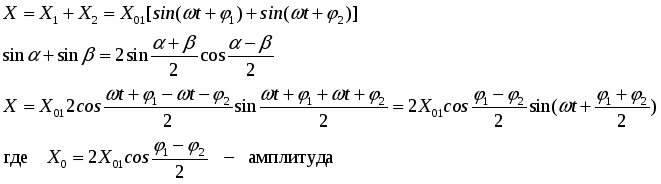
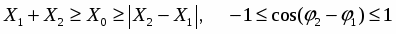
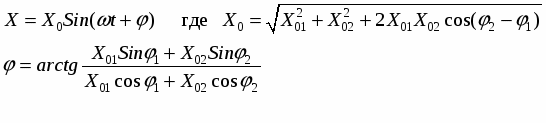
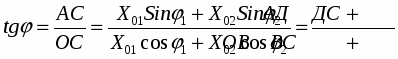
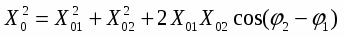
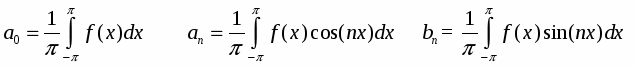
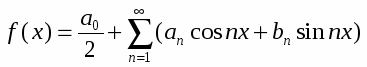
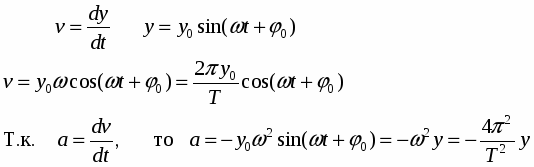
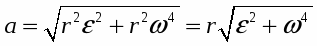
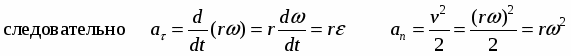
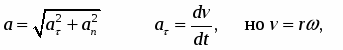
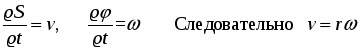
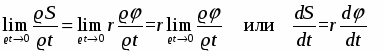
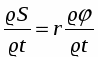
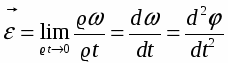
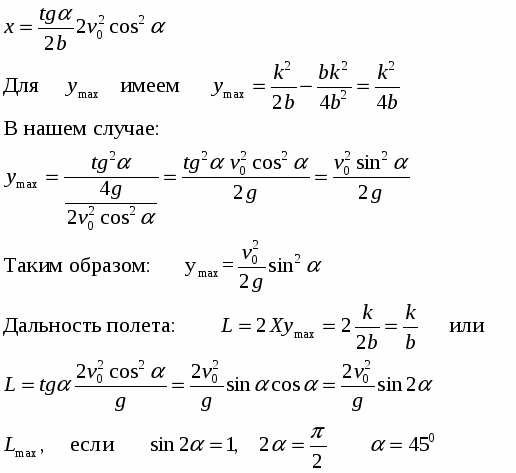
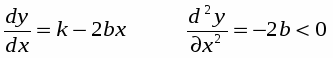
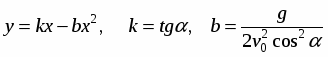
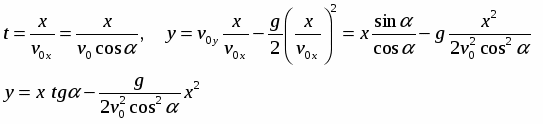
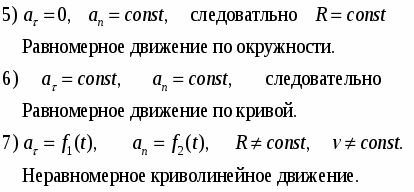
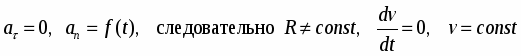
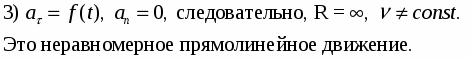
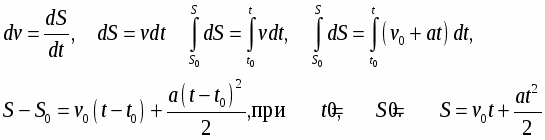
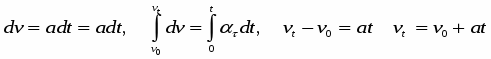
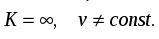
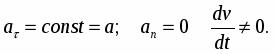
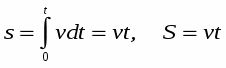
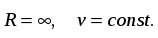
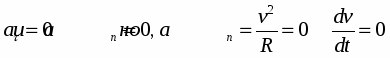
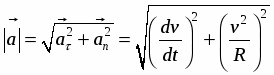
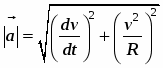
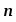
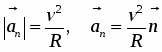
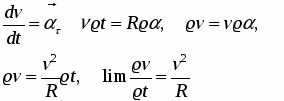
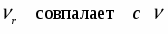
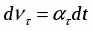
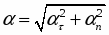
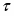
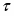
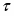
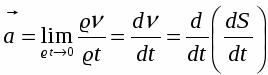
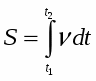
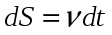
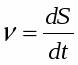
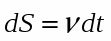
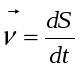
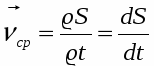
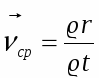
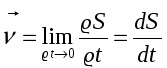
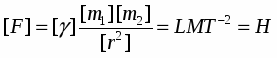
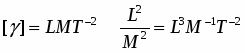
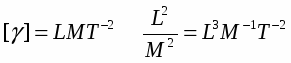
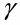
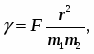
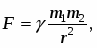
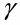
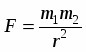
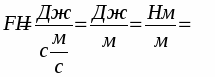
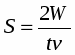
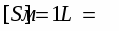
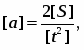
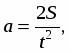
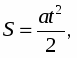
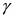
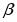
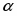
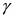
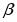
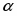
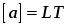ВВЕДЕНИЕ

Предмет физики и его связь со смежными науками.

Физика (природа в переводе с греческого) - одна из основных наук о природе, изучающая общие свойства и законы движения вещества физических полей.

В современном виде физика включает в себя следующие основные разделы:

1) механику;

2) акустику;

3) учение о теплоте;

4) учение об электричестве;

5) оптику;

6) молекулярную физику;

7) атомную физику;

8) физику элементарных частиц, атомного ядра и космических лучей;

9) учение о гравитационном поле.

Изучение курса физики при подготовке инженерных кадров важно 2-х точек зрения:

1. для выработки правильного диалектико-материалистического мировоззрения, т.е. обобщенное представление о мире в целом, т.к. различные физические законы и явления представляют собой прекрасные иллюстрации общих законов и принципов марксистско-ленинской философии.

2. физика является научной основой технического образования. Фундаментальные законы природы, изучаемые физикой - теоретическая база для развития техники. Физика сегодняшнего дня - это техника – это техника завтрашнего дня. Уже современная техника обладает такими огромными возможностями, что далеко превосходит вымыслы Жюль Верна. Открытия законов природы, сделанные учеными физиками, послужили основой технического прогресса человечества. Любая область техники развиваясь, опирается на знание физических законов, энергетика (учение об электричестве), космонавтика (механику), атомная энергия (атомную и ядерную физику).

Технические науки представляют собой как бы разросшиеся ветви на стволе физической науки. Таковы, например, электро- и радиотехника, теплотехника, астрофизика, биофизика и др.

Границы между физикой и другими естественными науками не могут быть установлены резко. Существуют обширные пограничные области:

физическая химия и химическая физика, биофизика, астрофизика, прикладная оптика и др.

Дальнейший прогресс нашего общества невозможен без науки вообще и физики в частности.

Изучение физики мы начинаем с механики.

Гл.1. Физические основы механики

Литература: I. Савельев И.В. Курс общей физики. - М.: Наука, 1989. -Т. I.

2. Сивухин Д.В. Курс •общей Физики. - М.: Наука, 1986. Т.

3. БерклеевскиЙ Курс физики. - М.: Наука, 1975-77. Т. I

4. Фанман Р., Лейтон Р. Файнмановские лекции по физике. • М.: Мир, 1977. Вып. 1-10.

5. Трофимова Т.И. Курс физики. - М.: Высшая школа, 1990.

6. Волькенштейн В.С. Сборник задач по общему курсу физики. - М.: Наука, 1987.

7. Хайкин С.Э. Физические основы механики. - М.: Наука, 1971.

8. Орир Д.К. Физика. - М.: Мир, 1981. Т. 1-2.

1. Механика, ее разделы и абстракции, применяемые при изучении движений

Механика - учение о простейшей форме движения материи, которое состоит в перемещении тел или их частей относительно друг друга. Механика - учение о механическом движении.

Механику обычно делят на 3 части: кинематику, статику, динамику,

В кинематике рассматривается движение тел вне связи с причинами, которые вызывают это движение или изменяют его.

В статике изучаются законы равновесия одного тела или системы тел.

Динамика рассматривает законы движения тел и причины, которые вызывают или изменяют движение.

При анализе сложных процессов, где трудно проследить и выявить основные причинные связи, стараются прежде всего отделить главные закономерности от второстепенных. При этом с целью упрощения рассматривают условную схему явления, пользуясь научными абстракциями. Без применения физических абстракций, отображающих только частично процесс или какую-либо из его сторон, любая, даже простейшая, задача будет разрешимой.

В механике пользуются следующими абстракциями: а) материальная точка; б) абсолютно твердое тело; в) абсолютно упругое тело и др.

Материальная точка - понятие применимое к такому телу, размерами которого можно пренебречь по сравнению с размерами, характеризующими движение этого тела.

Пример. - движение Земли вокруг Солнца. Землю и Солнце можно считать материальными точками, хотя их радиусы соответственно 6х10⁶ м. и 7х10⁸ м. Однако эти расстояния малы по сравнению с расстоянием между центрами этих небесных тел (1,5х10¹¹ м). Однако при изучении вращения Земли вокруг своей оси представление о Земле как о точке неприменимо.

Аналогично можно рассматривать движение океанского лайнера в порту и океане и т.д.

Совокупность нескольких тел, каждое из которых можно считать материальной точкой - называется системой материальных точек (наша Галактика) в некоторых случаях газ, состоящий из молекул.

Абсолютно твердое тело - система материальных частиц, расстояние между которыми не изменяется при произвольных перемещениях этой системы. А.т.т. - тело, которое ни при каких условиях не деформируется. Например, диск, совершающий крутильно-гармонические колебательные движения. Период колебания диска зависит только от массы, его размеров, однородности материала, из которого он изготовлен, распределения масс относительно центра, но не зависит от его упругих свойств. При этом отдельные части диска не изменяют своего положе относительно друг друга.

Абсолютно упругое тело - тело, основными характеристиками которого являются его упругие свойства. А.у.т. - тело, для которого силы однозначно определяют деформации и наоборот.

Правильность выбранной абстракции подтверждается совпадением, определенной точностью результатов теории и опыта.

Физика - наука, устанавливающая закономерные связи посредством наблюдений явлений в природе и посредством лабораторных опытов. Согласие результатов научного анализа с результатами опыта - критерий истинности наших познаний об окружающем мире.

2. Системы единиц измерения физических величин.

Измерить какую-либо физическую величину - это значит сравнить ее с другой однородной физической величиной, принятой за единицу I измерения. Следовательно, для измерения физических величин необходимо выбрать единицы измерения (эталоны). Эталоны можно выбрать произвольно, но они должны удовлетворять следующим требованиям:

а) легко воспроизводиться в любом количестве;

б) должны быть удобны для пользования в практической деятельности.

Выбор единиц, их хранение и воспроизведение определяются методологией, ВНИИ метрологии г. Ленинграда.

Чаще всего выбирают несколько эталонов для некоторых независимых физических величин и принимают их за основные. Эталоны (единицы измерения) всех остальных величин, называемые производными, получают, пользуясь физическими законами. Эталоны - это меры и измерительные приборы, предназначенные для хранения и воспроизведения единиц измерений с наивысшей достижимой при данном состоянии науки и техники точностью и принятые в общегосударственном или международном масштабе.

Совокупность основных и производных единиц образуют системы единиц. Т.к. выбор основных единиц произволен, то может быть построен целый ряд систем единиц СГС, в мех. СГСЭ, в эл. МКС МКГСС и др. В последнее время в качестве предпочтительной принята Международная система единиц СИ - единая система для всех разделов физики.

В этой системе основными единицами измерения являются:

длины L – 1 м

1.650.763,73 излучения оранжевого цвета изотопа криптона 86 в вакууме.

массы M – 1 кг

ед. массы, равная массе междуна-родного прототипа килограмма.

времени T – 1 с

время, равное 9192631770 периодам излучения линии 2 S 1/2 в спектре атома цезия-133.

температура T^o – 1 К

температура, равная 1/273,15 термодинамической температуры затвердевания дистиллированной воды при 101 325 Па.

количество в-ва v – 1 моль

количество вещества, содержащее столько атомов, сколько содержится в 0,012 кг нуклида у С₁₂.

сила тока J – 1А

Сила тока, который, проходя по двум || прямым проводникам  длина и ничтожного сечения, расположенных на расстоянии 1 м в вакууме, вызывает силу 2х10^-7 Н на каждый метр длины.

сила света Jсв I Кд

Кандела. Сила света, испускаемого 1/600000 м² в  к этой поверхности направлении при т-ре затвердевания платаны и при давлении 101 325 Па.

Дополнительные

1 рад – единица плоского угла.

1 ср – стерадиан - единица телесного угла.

1.3. Размерность физических величин.

Размерностью физических величин называется соотношение, на основании которого можно судить об изменении единицы сложной величины вследствие изменения основных единиц.

Так для ускорения ^-2

Это значит, что при увеличении единицы пути в n раз, в n раз увеличится и ускорение. При увеличении в m раз единицы времени, единица ускорения уменьшится в m² раз.

Формулы размерностей единиц сложных величин устанавливают закономерности, связывающие физические величины.

Обозначим размерности так:

[F]- размерность силы; [v] - размерность скорости; [а] - размерность ускорения и т.д.

L=[l] - размерность длины; [m]=M - размерность массы;

[t]=T - размерность времени.

Размерность любой физической величины в механике можно записать

LMT

где ,, - любые целые, дробные, + и - числа, в частности они могут быть равны 0.

Т.к. физические законы не зависят от выбора единиц измерения, входящих в них физических величин, то размерности обеих частей уравнений этих законов должны быть одинаковыми.

Это правило используется для проверки правильности полученного результата, а также для установления размерностей физических величин.

Например, 1) установим размерность силы [F] в СИ

F=ma, [F]=[m][a], [m]=кг=М,

[t]=1c=T, [a]=LT^-2,

[F]=MLT^-2 –формула размерности.

2) При решении задачи по определению силы получено выражение

W - энергия; t - время; v - скорость.

Известно, что сила в СИ измеряется в Ньютонах. Подставив в это выражение размерности входящих величин, мы можем убедиться в правильности полученного результата:

Иногда размерности частей уравнений не совпадают, тогда для устранения этого недостатка в правую часть выражения добавляют коэффициент пропорциональности. Значения К определяют опытным путем, а их размерности получают из основных законов.

Р

Например. Закон всемирного тяготения утверждает, что

но размерность [F] = LMT^-2, не соответствует размерности из этой формулы [F]=L^-2M². Для устранения недостатка введен коэффициент пропорциональности – гравитационная постоянная, численное значение которой определено экспериментально (в СИ = 6,67х10^-11 м/кг*с²), а размерность из закона тяготения: []=L³M^-1T^-2,

Таким образом:

2. Кинематика.

1. Системы отсчета и описание движения.

Механическое движение - процесс изменения положения тела или его частей по отношению к другим телам или друг другу.

Для описания механического движения необходимо указать тело, относительно которого рассматривается движение.

Произвольно выбранное неподвижное тело, по отношению к которому рассматривается движение данного тела, называется телом отсчета.

М(х, у, z)

z

х

у

0

r

Связанная с этим телом произвольная система координат, называется системой отсчета. Чаще всего используют декартову прямоугольную систему.

Положение точки однозначно определяется 3-мя координатами М (х, у, z).

x = f₁(t)

y = f₂(t)

z = f₃(t)

Эти уравнения являются уравнениями движения материальной точки. Совокупность последовательных положений точки М в процессе ее движения, называется траекторией движения точки.

Для определения уравнения траектории необходимо исключить из уравнения время.

С точки зрения кинематики никакого различия между разными системами отсчета нет, они все совершенно равноценны.

Лекция 2.

Величины, характеризующие движение.

Поступательное движение.

Простейшим видом механического движения абсолютно твердого тела является поступательное движение - такое движение, при котором тело перемещается параллельно самому себе. При этом все точки описывают конгруэнтные (одинаковые) траекторий, смещенные друг относительно друга.

Поступательное движение абсолютно твердого тела может быть охарактеризовано движением какой-либо одной его точки, например, центра масс.

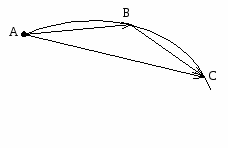
Для характеристики поступательного движения тела (материальной точка) вводится понятие перемещения.

Перемещением называется вектор, соединяющий начальное положение тела с его конечным положением.

A

B

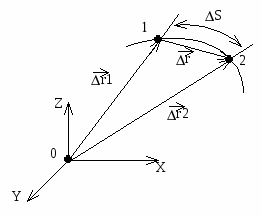
Если положение точки в декартовой системе координат задано радиус-вектором, то перемещение можно определить как разность радиус векторов, характеризующих конечное (2) и начальное (1) положения точки, движущейся в течение промежутка времени t = t₂ - t₁ r = r₂ - r₁

Проекции вектора перемещения на координатные оси 0Х, 0У, 0Z

z_x = x₂ – x₁ = x

z_y = y₂ – y₁ = y

z_z = z₂ – z₁ = z

x, y, z – перемещение точки вдоль соответствующих осей.

В общем случае перемещение не совпадает с траекторией движения. Достаточно малое перемещение, которое с определенной степенью точности можно считать совпадающим с соответствующим участком траектории, называется элементарным перемещением S. Расстояние, пройденное телом при его движении по траектории, равно пути S. Путь - величина скалярная. В частных случаях перемещение и путь могут совпадать.

Мгновенная линейная скорость - физическая величина» равная пределу, к которому стремится отношение элементарного перемещения S за промежутку времени t в течение которого совершается это перемещение, при t 0.

Мгновенная скорость - векторная величина, имеющая тоже направление, что и касательная к траектории, т.к. вектор мгновенной скорости v совпадает с вектором достаточно малого перемещения dS за достаточно малое время dt. Мгновенная скорость численно равна первой производной от перемещения по времени.

Средняя скорость за промежуток времени t = t₂ - t₁ – это физическая величина, равная отношению вектора перемещения z к длительности промежутка времени t.

Средняя скалярная (путевая) скорость - физическая величина, определяемая отношением пути S, пройденного точкой за промежуток времени t к длительности этого промежутка:

Т.к. , то ,

, ,

Величину пройденного точкой пути можно представить графически площадью фигуры ограниченной кривой v = f (t) прямыми t = t₁ и t = t₁ и осью времени на графике скорости.

При движении точки мгновенная скорость может меняться как по величине, так и по направлению. При этом вектор стремится к некоторому пределу, называемому линейным ускорением:

Т.о., ускорение - векторная величина, характеризующая изменение скорости в единицу времени, численно равная первой производной от мгновенной

скорости по времени или второй производной от перемещения по времени.

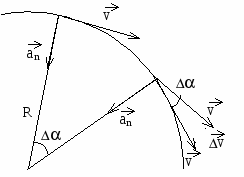
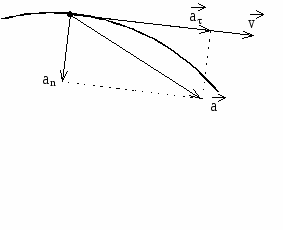
В общем случае ускорение не совпадает по направлению с вектором скорости. Вектор ускорения а может быть представлен в виде 2-х взаимно перпендикулярных векторов: а_n – нормального ускорения, а – тангенциального ускорения. а направлена вдоль касательной к траектории движения.

Полное ускорение а = а_n + а Численное значение полного ускорения

За малый промежуток времени dt тангенциальное ускорение изменяет скорость на величину .

, следовательно, тангенциальное ускорение изменяет только величину скорости

Нормальное ускорение а_n изменяет только направление скорости, численное значение а_{n ,}

где - единичный вектор нормали к траектории движения.

Полное ускорение точки численно можно определить так:

Отметим, что при поступательном движении твердого тела все его точки имеют одинаковые скорости и ускорения и описывают одинаковые траектории, смещенные относительно друг друга.

Классификация движений.

Для классификаций движений воспользуемся формулой для определения полного ускорения

Предположим, что

1)

Следовательно, Это случай равномерного прямолинейного движения.

Но

2) Следовательно

Это случай равномерного движения. В этом случае

При v₀ = 0 v_t = at – скорость равноускоренного движения без начальной скорости.

4)

Криволинейное движение с постоянной скоростью.

Лекция 3.

Движение тела, брошенного под углом к горизонту.

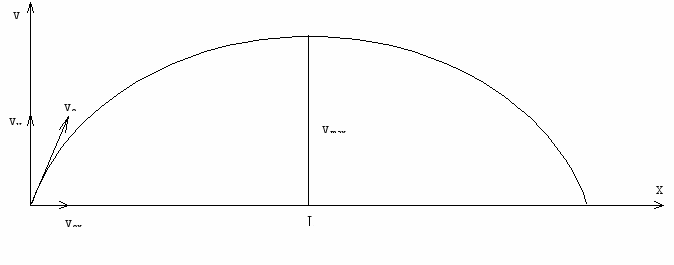
В качестве сложного движения рассмотрим движение точечной массы брошенной под углом  к горизонту со скоростью v₀.

В этом случае точка одновременно движется равномерно со скоростью v_ox вдоль оси Х и равнозамедленно с начальной скоростью v_y вдоль оси У. ( а = g )

Уравнение движения точки имеют вид:

x = v_0xt, где v_0x = v₀ cos α

y = v_0yt – gt²/2, где v_0y = v₀ sin α

Для нахождения уравнения траектории движения необходимо из системы уравнений исключить время:

Полученное выражение представляет собой уравнение параболы:

Для нахождения y_max необходимо найти первую производную указанной функции по Х и приравнять ее к нулю, определить вторую производную и исследовать ее знак. Если вторая производная меньше 0, то функция действительно имеет максимум.

Следовательно, у = y_max при x=k/2b т.е.

Все записанное справедливо, если отсутствует или достаточно мало сопротивление среды, в которой движется материальная точка. Таким образом, наибольшая дальность полета в отсутствии сил сопротивления наблюдается при движении тела под углом в 45° к горизонту.

Вращательное движение.

Другим простейшим видом механического движения является вращательное движение абсолютно твердого тела. При таком движении его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат на одном прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения.

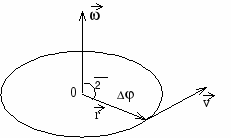
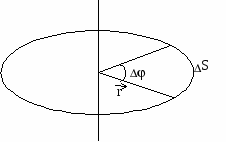
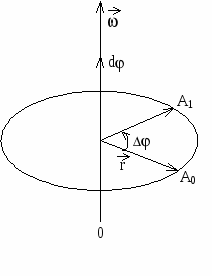
Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением. Угол поворота φ - это угол, считанный между двумя последовательными положениями радиуса вектора r, соединяющего тело или материальную точку с осью вращения.

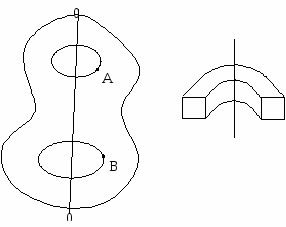
Угловая скорость ω - векторная физическая величина, показывающая, как изменяется угол поворота в единицу времени и численно равная первом производной от угла поворота по времени.

Направление вектора ω совпадает с направлением аксиального вектора Δφ, т.е. такого, который имеет длину численно равную углу Δφ в определенном масштабе, а направление совпадающее с осью вращения и определяемое правилом правого винта.

При равномерном вращении ω = const. Следовательно ω = φ / t.

Равномерное вращение характеризуется периодом вращения Т , т.е. временем, за которое тело делает один полный оборот, круговой частотой ω = 2π / Т, частотой γ = 1/Т

и числом оборотов в единицу времени n.

Угловая скорость может меняться как по величине, так и по направлению. Векторная величина, характеризующая изменение угловой скорости в единицу времени и численно равная второй производной от угла поворота по времени, называется угловым ускорением:

Если положение и радиус окружности, по которой происходит вращение не изменяется со временем, то έ совпадает по направлению с направлением ω в случае ускоренного вращательного движения и противоположна в случае замедленного вращения.

Связь между линейной и угловой скоростью и ускорением.

Отдельные точки вращающегося тела имеют различные линейные скорости v , которые непрерывно изменяют свое направление и зависят от ω и расстояния r соответствующей точке до оси вращения.

Точка, находящаяся на расстоянии r от оси вращения проходит путь ΔS = rΔφ.

Поделим обе части равенства на Δt:

, при Δt 0 получим пределы от левой и правой частей равенства:

Но

Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. Известно, что

Откуда

Из написанных формул видно, что a_τ, a_n и a растут с увеличением расстояния точек до оси вращения. Формула v = ωr устанавливает связь между модулями векторов v, r, и ω, которые перпендикулярны друг к другу.

Т.к. ω | r ,то можно написать v = ω∙r∙sina это ничто иное как модуль векторного произведения. Таким образом

v = [ ω r ]

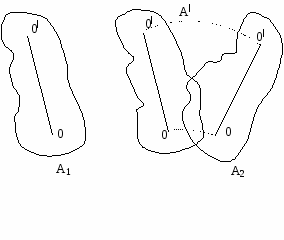
Рассмотренные простейшие виды движения твердого тела важны потому,

что любое движение твердого тела сводится к ним.

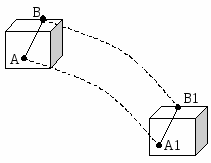
Рассмотрим два последовательных положения тела А₁ и А₂. Из положения А₁ в положение А₂ тело можно перевести следующим образом: вначале А₁ в А¹ поступательно. Затем из положения А¹ в положение А₂ путем поворота на угол φ вокруг произвольной точки 0.

Следует отметить, что в вращательному движению применимы все формулы кинематики материальной точки с заменой в них линейных величин на соответствующие угловые.

Например:

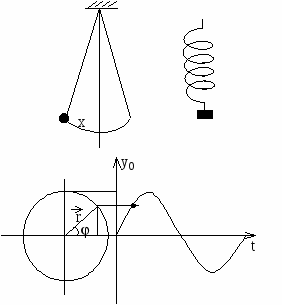
Колебательное движение.

Колебаниями или колебательными движениями являются движения или изменения состояния, обладающие той или иной степенью повторяемости во времени. Колебания весьма разнообразны по своей природе: колебания пружинного маятника, качания маятников, колебания струн, вибрации фундаментов, качка корабля, колебания ветвей деревьев и т.д.

Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени: положение маятника в часах, Т – период, v = 1/T.

При изучении кинематики колебательных движений нас интересуют:

- закон, по которое повторяется движение;

- время, через которое тело (система) снова приходит к тому же самому состоянию;

- наибольшие отклонения, которых достигает движущееся тело и т.д.

Изучив эти характеристика колебательного движения, мы можем определить состояние тела (системы) в любой момент времени.

Все сложные виды колебательных движений можно свести к простейшим гармоническим колебаниям. Гармоническими колебаниями физической величины a называется процесс изменения ее во времени по закону sin или cos.

Например: колебания математического маятника, x = x₀cosωt колебания пружинного маятника.

Аналогично колебательного движения можно получить, если рассмотреть закон изменения проекции точки, движущейся по окружности на линию, лежащую в плоскости движения точки.

Если радиус окружности r, угловая скорость вращения ω , то проекция

y = r sinφ = r sinωt

если было начальное смещение на φ_0,

y = r sin ( ωt + φ₀ )

Аргумент синуса (или cos) наз. фазой. Фаза определяет положение колеблющейся величины в данный момент времени. φ₀ – начальная фаза, которая определяет положение точки в начальный момент времени t = 0

y = y₀ sinφ₀

ω - круговая или циклическая частота, т.е. число полных колебаний, которые совершаются за 2π единиц времени:

ω = 2πv = 2π/Т

где v - частота колебаний, т.е. число полных колебаний за единицу времени;

Т - период колебания - наименьший промежуток времени, по истечении которого повторяются значения всех величин, характеризующих колебательное движение, т.е. время, за которое совершается полное колебание; у – смещение точки - удаление от положения равновесия в данный момент времени; у₀ - амплитуда колебания - (наибольшее значение колеблющейся функции).

Вычислим скорость и ускорение точки, совершающей гармоническое колебание:

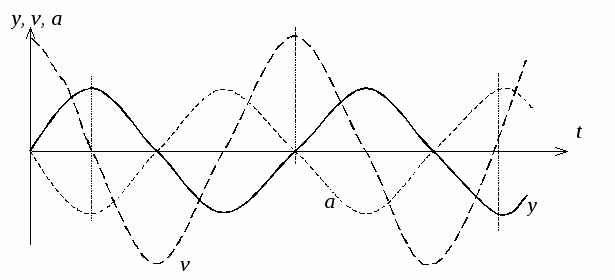
Знак " – " означает, что ускорение направлено в сторону, противоположную смещению. Изменение y, v, a с течением времени можно представить так:

t

y

v

a

0

0

ωy₀

0

T/4

y₀

0

– ω² y₀

T/2

0

– ωy₀

0

3T/4

– y₀

0

ω² y₀

T

0

ωy₀

0

Графически эти зависимости имеют вид:

Из таблицы и графика следует, что скорость имеет максимальные значения, когда точка проходит положения равновесия, а ускорение максимально в крайних положениях.

Сложение колебаний

Из теорий гармонического анализа известно, что любую периодическую функцию f(x), имеющую период 2π, можно представить в виде тригонометрического ряда:

где a₀, a_n, b_n - коэффициенты этого ряда, определяемые по формулам:

Следовательно, любое сложное колебание можно представить как сумму нескольких простых. Чтобы знать, как зависят параметры сложного колебания от соотношения частот, амплитуд, фаз и направлений слагаемых колебаний, рассмотрим наиболее простые случаи сложения гармонических колебаний.

1. Сложение двух колебаний одного направления.

а) сложение 2-х колебаний одинаковой частоты.

ω₁ = ω₂ = ω, Т₁ = Т₂ = Т Уравнения колебаний отличаются только начальной фазой и амплитудой и имеют вид:

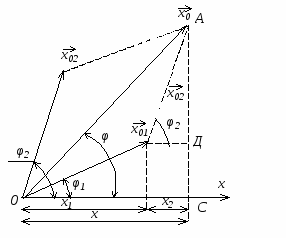
Представим оба колебания в виде векторов амплитуды Х₀₁ и Х₀₂, Сложение векторов выполним графически.

Отложим от точки 0 под углом φ₁ – вектор Х₀₁, под углом φ₂ – вектор Х₀₂. Обе амплитуды вращаются с одинаковой угловой скоростью и против часовой стрелки. Следовательно, угол между амплитудами остается постоянным, равным (φ₂ – φ₁). Вектор Х₀ представляет собой гармоническое колебание, происходящее с той же частотой и амплитудой │Х₀│= │Х₀₁+ Х₀₂│ и начальной фазой φ. Из чертежа

Само результирующее колебание имеет вид:

Важно заметить, что амплитуда результирующего колебания зависит от разности фаз (φ₂ – φ₁) слагаемых колебаний.

Она заключена в пределах:

1. Если разность начальных фаз слагаемых колебаний, равна четному числу π, φ₂ – φ₁ = кπ , то Х₀ = Х₀₁ + Х₀₂, tg φ = tg φ₁, φ = φ₁, к = 0,1,2, …

Колебания однофазные и усиливают друг друга.

Х

Х

Х₁

Х₂

t

2) Если φ₂ – φ₁ = (2к+1)π , то Х₀ = Х₀₁ - Х₀₂ , к = 0,1,2,… следовательно колебания ослабляют друг друга

Х

t

3) Если Х₀₁ = Х₀₂ , ω₁ = ω₂ = ω , φ₂ = φ₁

Уравнение результирующего колебания имеет вид:

– начальная фаза результирующего колебания.

Результирующее колебание гармоническое, отличающееся по фазе от слагаемых колебаний на половину суммы их начальных фаз.

t

x

При φ₁ – φ₂ = 2кπ , (к = 0,1,2,…) Х₀ = 2Х₀₁ – колебания усиливаются.

t

х

При φ₁ – φ₂ = (2к + 1)π , (к = 0,1,2,…) Х₀ = 0 – колебания гасятся.

t

х

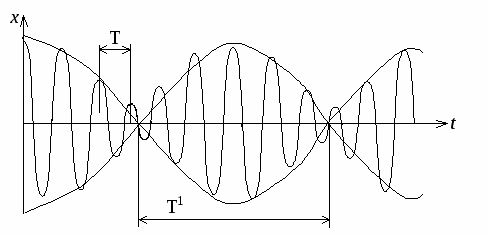
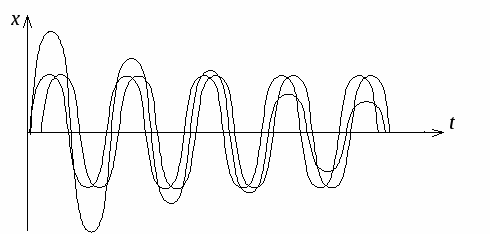
2. Биения.

Особый интерес представляет сложение колебаний одинакового направления с одинаковыми амплитудами, имеющими (близкие) мало отличающиеся частоты.

Результирующее суммарное колебание имеет уравнение:

Полученное выражение представляет собой произведение 2-х гармонических сомножителей с частотами и .

Если ω₁ мало отличается от ω₂ , то частота имеет близкие значения к ω₁ и ω₂ , а частота – будет очень мала, т.е.

Отсюда следует, что результирующее колебание можно рассматривать как гармоническое колебательное движение, происходящее с круговой частотой , периодом и амплитудой

Причем амплитуда не остается постоянной, а медленно изменяется со временем. Частота изменения амплитуды ,

а период амплитуды

Такие колебания называются биениями. Биения - такие колебания, амплитуда которых периодически возрастает и убывает по закону cos. Максимальная амплитуда наблюдается, если фазы слагаемых колебаний совпадают. Ясли эти колебания находятся в противофазе, то они гасят друг друга.

Биения часто встречаются при сложении колебаний и широко используются в радиотехнике.

2. Сложение взаимно перпендикулярных колебаний.

1. Рассмотрим движение точки М₁, участвующей одновременно в 2-х взаимно перпендикулярных колебаниях, частоты которых ω₁ и ω₂ равны (ω₁ = ω₂ = ω), амплитуды соответственно а и в.

Колебательный процесс в этом случае описывается системой уравнений:

где φ – угол сдвига фаз.

Для определения уравнения траектории движения точки из системы уравнений исключим время. Из первого уравнения

Второе уравнение перепишем в виде:

Подставив вместо sin ωt и cos ωt их значения будем иметь уравнение движения

Исследуем некоторые частные случаи.

а) при равенстве частот имеет место еще и равенство фаз, т.е. φ = 0.

Уравнение траектории имеет вид

Уравнение прямой, проходящей через начало координат под углом ά:

y

x

в

- в

а

- а

Смещение от начала координат определяется уравнением

Т.к. уравнение слагаемых колебаний имеет вид

y

x

в

- в

а

- а

Таким образом результирующее движение является гармоническим колебанием.

б) составляющая колебания отличается по фазе на π/2 . Уравнение траектории имеет вид:

отсюда

- эллипс с плоскостями a и b.

a

в

y

x

При равенстве амплитуд траектории представляют собой окружность.

y

x

2) При сложении взаимно перпендикулярных колебаний, частоты которых кратны между собой, например ω₁ : ω₂ = 1/2 , 2/3 и т.д. = m/n ,

где m и n – целые числа, колеблющееся тело описывает сложные кривые (наз. Фигурами Лисажу), форма которых определяется отношением частот складываемых колебаний, их амплитудой и разностью фаз между ними

ω₁ : ω₂ = 2 : 1 ω₁ : ω₂ = 3 : 2

Δφ = 0 Δφ = π / 2 Δφ = 0 Δφ = π / 4