Реле часу
Лабораторна робота
Стислі теоретичні відомості
Трансформатори
Трансформатором називається статичний електромагнітний пристрій, який має дві (або більше) обмотки, які зв`язані між собою індуктивно, і призначений для перетворення первинних у вторинні параметри змінного струму. В загальному випадку вторинні параметри змінного струму можуть відрізнятися від первинних значенням напруги, струму, числом фаз, формою кривої напруги (струму). За системою змінного струму трансформатори поділяють на трифазні рис. 21.1а та однофазні рис. 21.1б.
Рис. 21.1
а
б
За призначенням трансформатори поділяються на силові та спеціальні. Силові трансформатори використовуються в колах автоматики, телемеханіки, зв`язку, апаратури живлення та електропобутових пристроях.
б
Рис. 21.2
а
Спеціальні трансформатори – це перетворювальні, технологічні, вимірні пік та інші.
Аналіз роботи трансформатора проведемо на прикладі однофазного понижувального трансформатора з двома обмотками (рис. 21.3).
Трансформатор складається зі стального осердя зібраного з тонких листів електротехнічної сталі, що ізольовані одне від одного для зменшення магнітних втрат.
I1
ФР2
Ф0
U2
Рис. 21.3
I2
ФР1
U1
На стержнях однофазного трансформатора (рис. 21.3) розміщені дві обмотки 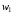 число витків первинної
число витків первинної 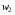 число витків вторинної обмотки які виконані з ізольованого проводу. До первинної обмотки підводиться напруга живлення
число витків вторинної обмотки які виконані з ізольованого проводу. До первинної обмотки підводиться напруга живлення 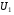 , а з вторинної знімається напруга
, а з вторинної знімається напруга 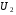 , що підводиться до споживача електричної енергії.
, що підводиться до споживача електричної енергії.
Струм первинної обмотки трансформатора 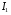 збуджує змінний магнітний потік
збуджує змінний магнітний потік 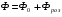 частина якого замикається в осерді
частина якого замикається в осерді 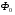 - решту
- решту 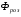 розсіюється поза магнітопроводом
розсіюється поза магнітопроводом 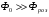
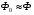 Магнітний потік
Магнітний потік 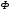 змінюється за синусоїдним законом
змінюється за синусоїдним законом 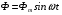 , зчіплений з витками первинної
, зчіплений з витками первинної 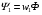 і вторинної
і вторинної 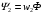 обмоток трансформатора індукує електрорушійні сили
обмоток трансформатора індукує електрорушійні сили 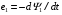 самоіндукції і
самоіндукції і 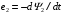 взаємоіндукції.
взаємоіндукції.
Індуковані електрорушійні сили
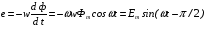 ,
,
де 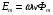 а діюче значення
а діюче значення 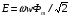 . Індуковані електрорушійні сили самоіндукції
. Індуковані електрорушійні сили самоіндукції 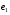 та взаємоіндукції
та взаємоіндукції 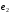 індукції в трансформаторі відстають від магнітного потоку на кут
індукції в трансформаторі відстають від магнітного потоку на кут 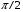 .
.
Струм первинної обмотки трансформатора без навантаження є струмом холостого ходу, намагнічуючим струмом. Нехтуючи впливом насичення, несинусоїдний струм можна замінити еквівалентним синусоїдним.
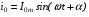
де 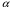 -кут магнітних втрат (кут фазового зсуву між струмом і магнітним потоком), зумовлений втратами потужності в магнітопроводі трансформатора. Значення кута
-кут магнітних втрат (кут фазового зсуву між струмом і магнітним потоком), зумовлений втратами потужності в магнітопроводі трансформатора. Значення кута 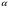 для сучасних електротехнічних сталей, як правило, невелике і складає 4-6 град.
для сучасних електротехнічних сталей, як правило, невелике і складає 4-6 град.
За другим законом Кірхгофа рівняння електричного стану для первинної та вторинної обмоток мають вигляд:
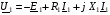 , \
, \ ,
,
де - 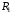
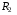 активні та
активні та 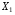
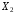 - індуктивні опори первинної та вторинної обмоток (індуктивні опори зумовлені потоками розсіювання). При ненасиченій магнітній системі діючі значення електрорушійних сил, що наводяться в первинній і вторинній обмотках трансформатора, визначаються за формулами:
- індуктивні опори первинної та вторинної обмоток (індуктивні опори зумовлені потоками розсіювання). При ненасиченій магнітній системі діючі значення електрорушійних сил, що наводяться в первинній і вторинній обмотках трансформатора, визначаються за формулами:
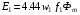 ,
, 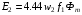 ,
,
де 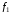 - частота змінного струму,
- частота змінного струму, 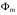 - амплітуда магнітного потоку трансформатора,
- амплітуда магнітного потоку трансформатора, 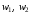 - число витків первинної і вторинної обмоток трансформатора. Відношення електрорушійної сили первинної обмотки трансформатора до електрорушійної сили вторинної обмотки, що дорівнює також відношенню відповідних чисел витків обмоток, називається коефіцієнтом трансформації трансформатора:
- число витків первинної і вторинної обмоток трансформатора. Відношення електрорушійної сили первинної обмотки трансформатора до електрорушійної сили вторинної обмотки, що дорівнює також відношенню відповідних чисел витків обмоток, називається коефіцієнтом трансформації трансформатора: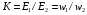 . В електротехніці коефіцієнтом трансформації
. В електротехніці коефіцієнтом трансформації 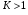 . Якщо
. Якщо 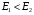 , то трансформатор є підвищувальним, якщо ж
, то трансформатор є підвищувальним, якщо ж 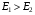 , то понижувальним.
, то понижувальним.
На відміну від режиму холостого ходу, що виникає в процесі експлуатації трансформатора, при дослідженні трансформатора є необхідність проведення досліду холостого ходу. Дослід холостого ходу проводиться для визначення коефіцієнту трансформації 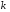 , магнітного потоку
, магнітного потоку 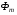 , а також магнітних втрат потужності
, а також магнітних втрат потужності 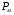 в осерді магнітопроводу трансформатора в номінальному режимі.
в осерді магнітопроводу трансформатора в номінальному режимі.
В досліді холостого ходу до первинної обмотки трансформатора підводиться номінальна напруга 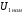 . Вторинна обмотка трансформатора при цьому розімкнена і струм у вторинній обмотці буде рівним нулю (
. Вторинна обмотка трансформатора при цьому розімкнена і струм у вторинній обмотці буде рівним нулю (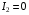 ). В первинній обмотці трансформатора буде протікати струм холостого ходу
). В первинній обмотці трансформатора буде протікати струм холостого ходу 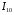 , значення якого невелике і складає в середньому
, значення якого невелике і складає в середньому 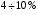 від номінального значення струму в первинній обмотці
від номінального значення струму в первинній обмотці 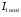 .
.
Скориставшись другим законом Кірхгофа для первинного та вторинного кола трансформатора в режимі холостого ходу, маємо рівняння електричного стану:
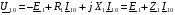 ,
,
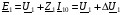 ,
, 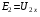 .
.
-E1
Ip
I
RI
XI
U1
Фm
Ia
Рис. 21.4
Враховуючи, що 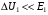 , тобто нехтуючи впливом падіння напруги
, тобто нехтуючи впливом падіння напруги 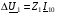 в первинній обмотці, отримаємо наближено
в первинній обмотці, отримаємо наближено 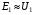 , що дорівнює добутку струму холостого ходу на опір первинної обмотки
, що дорівнює добутку струму холостого ходу на опір первинної обмотки 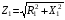 (із-за його невеликого значення у порівнянні з
(із-за його невеликого значення у порівнянні з 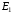 ). Рівнянню електричного стану відповідає векторна діаграма трансформатора для режиму холостого ходу (рис. 21.4).
). Рівнянню електричного стану відповідає векторна діаграма трансформатора для режиму холостого ходу (рис. 21.4).
Коефіцієнт трансформації 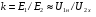 . Одержаний вираз дає змогу визначити магнітний потік та магнітну індукцію, якщо відомо поперечний переріз осердя магнітопроводу
. Одержаний вираз дає змогу визначити магнітний потік та магнітну індукцію, якщо відомо поперечний переріз осердя магнітопроводу 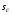 :
: 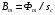 .
.
Потужність яку споживає трансформатор при холостому ході 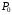 , складається із магнітних втрат
, складається із магнітних втрат 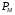 в осерді і електричних втрат
в осерді і електричних втрат 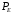 в обмотці в
в обмотці в 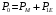 . Оскільки активний опір первинної обмотки
. Оскільки активний опір первинної обмотки 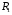 та струм холостого ходу
та струм холостого ходу 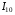 трансформатора, є незначними, електричні втрати невеликими і ними можна знехтувати в порівнянні з магнітними втратами
трансформатора, є незначними, електричні втрати невеликими і ними можна знехтувати в порівнянні з магнітними втратами 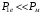 . Тому можна вважати, що потужність, яку споживає трансформатор в досліді холостого ходу і вимірюється ватметром, визначає магнітні втрати, що зумовлені втратами на гістерезис та вихрові струми
. Тому можна вважати, що потужність, яку споживає трансформатор в досліді холостого ходу і вимірюється ватметром, визначає магнітні втрати, що зумовлені втратами на гістерезис та вихрові струми 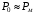 .
.
При навантаженні трансформатора до його вторинної обмотки під’єднується споживач електричної енергії. Струм у вторинній обмотці навантаженого трансформатора за законом Ома визначається виразом 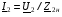 , де
, де 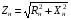 повний опір споживача. За другим законом Кірхгофа для первинної і вторинної обмоток навантаженого трансформатора можна записати наступні рівняння електричної рівноваги:
повний опір споживача. За другим законом Кірхгофа для первинної і вторинної обмоток навантаженого трансформатора можна записати наступні рівняння електричної рівноваги:
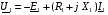 ,
, 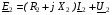 ,
,
де  - струм первинної обмотки трансформатора,
- струм первинної обмотки трансформатора, 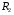 - активний опір вторинної обмотки,
- активний опір вторинної обмотки, 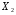 - реактивний опір вторинної обмотки, зумовлений потоками розсіювання.
- реактивний опір вторинної обмотки, зумовлений потоками розсіювання.
Оскільки спад напруги на первинній обмотці трансформатора 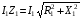 в межах до номінального струму навантаження є невеликим у порівнянні з електрорушійною силою
в межах до номінального струму навантаження є невеликим у порівнянні з електрорушійною силою 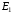 , то можна наближено вважати, що
, то можна наближено вважати, що 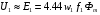 . З цього випливає, що при напрузі
. З цього випливає, що при напрузі 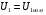 живлення електрорушійну силу
живлення електрорушійну силу 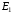 можна вважати сталою
можна вважати сталою 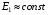 і практично незалежною від навантаження трансформатора. Оскільки електрорушійна сила наводиться результуючим магнітним потоком, то цей потік повинен також залишатися практично сталим в межах від режиму холостого ходу до номінального навантаження трансформатора, тобто
і практично незалежною від навантаження трансформатора. Оскільки електрорушійна сила наводиться результуючим магнітним потоком, то цей потік повинен також залишатися практично сталим в межах від режиму холостого ходу до номінального навантаження трансформатора, тобто 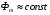 .
.
Дослідження роботи навантаженого трансформатора зручно проводити на основі векторних діаграм, побудованих для приведеного трансформатора, що замінює реальний трансформатор, у якого параметри вторинної обмотки приведені до напруги і числа витків первинної обмотки. Тому приведений трансформатор повинен мати коефіцієнт трансформації рівний одиниці (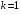 ).
).
В процесі визначення параметрів вторинної обмотки приведеного трансформатора всі параметри його первинної обмотки залишаються незмінними. При заміні реального трансформатора приведені активні, реактивні та повні потужності, а також коефіцієнт потужності вторинної обмотки трансформатора повинні залишатися сталими.
Значення приведеної вторинної електрорушійної сили 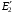 можна знайти з виразу для коефіцієнту трансформації:
можна знайти з виразу для коефіцієнту трансформації: 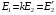 . Аналогічно можна записати вираз для приведеної вторинної напруги трансформатора
. Аналогічно можна записати вираз для приведеної вторинної напруги трансформатора 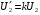 . Значення приведеного вторинного струму можна одержати зі співвідношення, отриманого з умови збереження незмінної потужності вторинної обмотки трансформатора:
. Значення приведеного вторинного струму можна одержати зі співвідношення, отриманого з умови збереження незмінної потужності вторинної обмотки трансформатора: 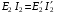 . Враховуючи це, а також
. Враховуючи це, а також 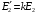 , одержуємо вираз для приведеного вторинного струму:
, одержуємо вираз для приведеного вторинного струму: 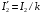 .
.
Приведений активний опір вторинної обмотки трансформатора 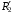 визначають виходячи з умови постійності електричних втрат у вторинній обмотці трансформатора в процесі приведення параметрів
визначають виходячи з умови постійності електричних втрат у вторинній обмотці трансформатора в процесі приведення параметрів 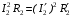 . Враховуючи вираз для струму
. Враховуючи вираз для струму 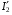 , одержимо вираз для приведеного активного опору вторинної обмотки
, одержимо вираз для приведеного активного опору вторинної обмотки 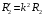 . Аналогічно, враховуючи незмінність реактивної та повної потужності вторинної обмотки трансформатора, можна одержати вирази для приведеного реактивного індуктивного та приведеного повного опорів вторинної обмотки трансформатора:
. Аналогічно, враховуючи незмінність реактивної та повної потужності вторинної обмотки трансформатора, можна одержати вирази для приведеного реактивного індуктивного та приведеного повного опорів вторинної обмотки трансформатора: 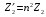 .
. 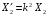
R1
Xр
I1
R22’
X2’
I2’
U1
X0
R0
Рис.21.5
U2’
I10
E1
Zн
E2’
Електрорушійну силу 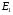 , що дорівнює
, що дорівнює 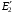 , як і для котушки індуктивності з магнітопроводом, можна замінити векторною сумою активного і реактивного індуктивного падінь напруги у відповідності з рівнянням
, як і для котушки індуктивності з магнітопроводом, можна замінити векторною сумою активного і реактивного індуктивного падінь напруги у відповідності з рівнянням 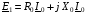 , де
, де 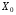 – індуктивний опір, що зумовлений основним потоком трансформатора;
– індуктивний опір, що зумовлений основним потоком трансформатора; 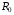 - активний опір, що зумовлений магнітними втратами потужності в магнітопроводі трансформатора, тобто деякий умовний активний опір, на якому виділяється потужність
- активний опір, що зумовлений магнітними втратами потужності в магнітопроводі трансформатора, тобто деякий умовний активний опір, на якому виділяється потужність 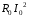 , що дорівнює магнітним втратам потужності в магнітопроводі.
, що дорівнює магнітним втратам потужності в магнітопроводі.
Враховуючи одержані рівняння для 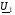 та
та 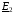 , використовуючи приведені параметри вторинної обмотки трансформатора, запишемо рівняння електричної рівноваги для вторинної обмотки
, використовуючи приведені параметри вторинної обмотки трансформатора, запишемо рівняння електричної рівноваги для вторинної обмотки 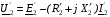 . Беручи до уваги, що
. Беручи до уваги, що 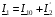 , можна скласти схему заміщення трансформатора, що має вигляд, зображений на рис. 21.5 і побудувати векторну діаграму.
, можна скласти схему заміщення трансформатора, що має вигляд, зображений на рис. 21.5 і побудувати векторну діаграму.
Дослід короткого замикання трансформатора проводиться для визначення електричних втрат потужності в проводах обмоток і параметрів спрощеної схеми заміщення трансформатора. Цей дослід проводиться при короткому замиканні вторинної обмотки трансформатора. При цьому напруга на вторинній обмотці рівна нулю (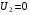 ).
).
Коротке замикання вторинної обмотки трансформатора в процесі експлуатації приводить до того, що при номінальній напрузі, яка підводиться до первинної обмотки, в обмотках трансформатора виникають досить значні струми, які можуть вивести його з ладу.
При проведенні досліду короткого замикання трансформатора, на відміну від небезпечного режиму короткого замикання, що виникає в аварійних умовах, до первинної обмотки трансформатора підводиться така напруга, при якій в його обмотках виникають струми рівні номінальним. Для цього достатньо до первинної обмотки трансформатора підвести понижену напругу 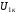 в
в 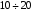 разів меншу (це залежить від типу і потужності трансформатора) у порівнянні з номінальним значенням напруги
разів меншу (це залежить від типу і потужності трансформатора) у порівнянні з номінальним значенням напруги 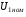 . Оскільки в досліді короткого замикання напруга, що підводиться до первинної обмотки мала
. Оскільки в досліді короткого замикання напруга, що підводиться до первинної обмотки мала 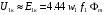 , то магнітний потік трансформатора
, то магнітний потік трансформатора 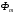 та магнітна індукція
та магнітна індукція 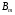 будуть також малими. Це означає, що втрати потужності в магнітопроводі
будуть також малими. Це означає, що втрати потужності в магнітопроводі 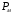 , що пропорційні квадрату магнітної індукції
, що пропорційні квадрату магнітної індукції 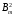 в досліді короткого замикання, мізерно малі і ними можна знехтувати.
в досліді короткого замикання, мізерно малі і ними можна знехтувати.
Таким чином, можна вважати, що в досліді короткого замикання вся потужність 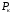 , що споживається трансформатором, йде на нагрівання його обмоток, тобто дорівнює електричним втратам
, що споживається трансформатором, йде на нагрівання його обмоток, тобто дорівнює електричним втратам 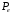 в проводах обмоток:
в проводах обмоток:
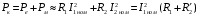 .
.
У вираз для 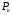 входять
входять 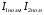 , тобто номінальні значення струмів у первинній та вторинній обмотках трансформатора, оскільки дослід короткого замикання проводиться при номінальному значенні струму. Тому, враховуючи що
, тобто номінальні значення струмів у первинній та вторинній обмотках трансформатора, оскільки дослід короткого замикання проводиться при номінальному значенні струму. Тому, враховуючи що 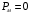 , потужність
, потужність 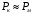 , тобто дорівнює електричним втратам потужності в обмотках трансформатора при номінальному навантаженні.
, тобто дорівнює електричним втратам потужності в обмотках трансформатора при номінальному навантаженні.
Отже, вимірявши напругу, струм та активну потужність в досліді короткого замикання (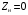 ), можна визначити параметри спрощеної схеми заміщення трансформатора (рис. 21.6)
), можна визначити параметри спрощеної схеми заміщення трансформатора (рис. 21.6)
R
Xр
I1
U
Рис. 21.6
R2’
X2’
U2’
Zн’
I2’
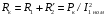 ,
, 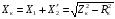 ,
,
де 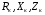 - відповідно активний, реактивний індуктивний та повний опори короткого замикання трансформатора. До навантажувальних характеристик трансформатора відносяться залежності вторинної напруги
- відповідно активний, реактивний індуктивний та повний опори короткого замикання трансформатора. До навантажувальних характеристик трансформатора відносяться залежності вторинної напруги 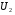 , коефіцієнта потужності
, коефіцієнта потужності 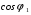 і коефіцієнта корисної дії
і коефіцієнта корисної дії 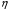 від струму навантаження
від струму навантаження 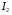 користувача електроенергії при
користувача електроенергії при 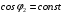 . Залежність напруги на затискачах вторинної обмотки від струму
. Залежність напруги на затискачах вторинної обмотки від струму 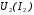 приведена на рис. 1.7 є зовнішньою характеристикою трансформатора.
приведена на рис. 1.7 є зовнішньою характеристикою трансформатора.
Вторинна обмотка трансформатора по відношенню до споживача електроенергії є джерелом, тому напрям струму у вторинній обмотці співпадає з напрямом електрорушійної сили 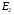 в цій обмотці. На підставі другого закону Кіргофа для вторинного кола трансформатора можна скласти рівняння електричної рівноваги для цього кола. Записавши його відносно напруги вторинної обмотки, одержимо рівняння зовнішньої характеристики трансформатора у векторній формі:
в цій обмотці. На підставі другого закону Кіргофа для вторинного кола трансформатора можна скласти рівняння електричної рівноваги для цього кола. Записавши його відносно напруги вторинної обмотки, одержимо рівняння зовнішньої характеристики трансформатора у векторній формі: 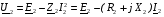 .
.
З отриманого виразу випливає, що зміна струму навантаження трансформатора приводить до зміни напруги на затискачах його вторинної обмотки. Це відбувається не лише за рахунок збільшення падіння напруги на вторинній обмотці, тобто збільшення добутку 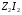 , а також за рахунок зменшення електрорушійної сили
, а також за рахунок зменшення електрорушійної сили 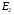 в реальних умовах із-за деякого зменшення магнітного потоку при збільшенні струму навантаження трансформатора.
в реальних умовах із-за деякого зменшення магнітного потоку при збільшенні струму навантаження трансформатора.
cos2<1 (інд.)
I2
Рис.21.7
cos2>1 (ємн.)
cos2=1
U2
cos1
I2
Рис.21.8
U2
cos0
Зовнішні характеристики трансформатора має вигляд показаний на рис. 21.7. З векторної діаграми навантаженого трансформатора можна встановити, що падіння напруги на його вторинній обмотці тим більше, чим більший кут зсуву фаз між електрорушійною силою 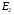 і струмом навантаження
і струмом навантаження 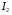 . При активно-індуктивному характері навантаження (
. При активно-індуктивному характері навантаження (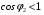 ) зі збільшенням струму
) зі збільшенням струму 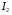 напруга
напруга 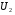 зменшується. При активно-ємнісному характері навантаження (
зменшується. При активно-ємнісному характері навантаження (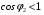 ) зі збільшенням струму
) зі збільшенням струму 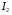 напруга
напруга 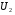 зростає. На рис. 1.8 представлена зовнішня характеристика трансформатора при активно-індуктивному навантаженні. В режимі холостого ходу трансформатора, при відсутності навантаження у вторинному колі, трансформатор споживає активну потужність, що дорівнює потужності холостого ходу
зростає. На рис. 1.8 представлена зовнішня характеристика трансформатора при активно-індуктивному навантаженні. В режимі холостого ходу трансформатора, при відсутності навантаження у вторинному колі, трансформатор споживає активну потужність, що дорівнює потужності холостого ходу
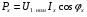 .
.
Оскільки потужність, струм і напруга в режимі холостого ходу не дорівнюють нулю, то не може бути рівним нулю 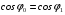 при
при 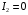 . Таким чином, залежність
. Таким чином, залежність 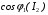 виходить не з початку координат, а з точки з ординатою, що дорівнює
виходить не з початку координат, а з точки з ординатою, що дорівнює 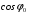 .
.
Зі збільшенням навантаження ця залежність спочатку досить різко зростає, досягає максимального значення при деякому значенні струму 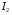 , а потім трохи зменшується при дальшому збільшенні струму навантаження, що можна побачити з векторної діаграми навантаженого трансформатора, оскільки зі збільшенням струму навантаження
, а потім трохи зменшується при дальшому збільшенні струму навантаження, що можна побачити з векторної діаграми навантаженого трансформатора, оскільки зі збільшенням струму навантаження 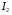 одночасно відбувається збільшення струму первинної обмотки трансформатора
одночасно відбувається збільшення струму первинної обмотки трансформатора  . Оскільки коефіцієнт потужності споживача постійний
. Оскільки коефіцієнт потужності споживача постійний 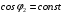 , то разом зі збільшенням вектора струму
, то разом зі збільшенням вектора струму 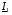 , відбувається його зміщення в сторону вектора
, відбувається його зміщення в сторону вектора 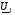 . Кут
. Кут 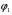 при цьому зменшується, а
при цьому зменшується, а 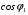 відповідно збільшується.
відповідно збільшується.
Проте, збільшення 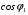 відбувається тільки до певної межі, що дорівнює
відбувається тільки до певної межі, що дорівнює 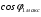 , оскільки подальше збільшення
, оскільки подальше збільшення 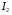 ,
, 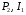 приводить до значного збільшення вектора реактивного падіння напруг на первинній обмотці
приводить до значного збільшення вектора реактивного падіння напруг на первинній обмотці 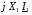 .
. При цьому зростання кута
При цьому зростання кута 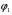 за рахунок збільшення вектора
за рахунок збільшення вектора 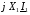 не може бути скомпенсованим зменшенням цього кута за рахунок збільшення струму
не може бути скомпенсованим зменшенням цього кута за рахунок збільшення струму  . Оскільки
. Оскільки 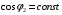 , струм
, струм 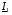 лише на межі може співпадати з лінією вектора струму
лише на межі може співпадати з лінією вектора струму 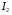 , що займає жорстко фіксоване положення на векторній діаграмі відносно вектора електрорушійної сили
, що займає жорстко фіксоване положення на векторній діаграмі відносно вектора електрорушійної сили 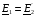 . При дальшому збільшенні струму навантаження відбувається зменшення коефіцієнта потужності
. При дальшому збільшенні струму навантаження відбувається зменшення коефіцієнта потужності 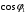 .
.
Дещо інший характер (рис.1.8) має залежність коефіцієнта корисної дії від струму навантаження 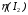 . Коефіцієнт корисної дії трансформатора - відношення корисної потужності до потужності, що споживається ним з мережі:
. Коефіцієнт корисної дії трансформатора - відношення корисної потужності до потужності, що споживається ним з мережі:
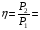
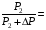
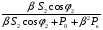
 ,
,
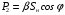 ,
, 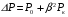 ,
,
де 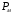 - втрати в магнітопроводі трансформатора (їх знаходять з досліду холостого ходу),
- втрати в магнітопроводі трансформатора (їх знаходять з досліду холостого ходу), 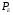 - електричні втрати в обмотках трансформатора (визначають при мінімальному навантаженні з досліду короткого замикання),
- електричні втрати в обмотках трансформатора (визначають при мінімальному навантаженні з досліду короткого замикання), 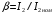 - відношення струму навантаження до його номінального значення,
- відношення струму навантаження до його номінального значення, 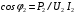 - коефіцієнт потужності споживача електроенергії.
- коефіцієнт потужності споживача електроенергії.
При відсутності навантаження (коли потужність не споживається) коефіцієнт корисної дії буде рівним нулю, тому графік залежності 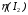 буде виходити з початку координат.
буде виходити з початку координат.
З формули для коефіцієнта корисної дії видно, що при малих значеннях навантаження, коли електричними втратами потужності 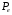 в обмотках трансформатора із-за невеликого значення струму навантаження можна знехтувати і коли втрати потужності в магніторповоді
в обмотках трансформатора із-за невеликого значення струму навантаження можна знехтувати і коли втрати потужності в магніторповоді 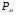 будуть співрозмірні з корисною потужністю
будуть співрозмірні з корисною потужністю 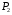 , значення коефіцієнта корисної дії трансформатора зростатиме.
, значення коефіцієнта корисної дії трансформатора зростатиме.
Втрати потужності в магнітопроводі трансформатора не залежать від навантаження, в той час як зі збільшенням навантаження електричні втрати потужності в обмотках трансформатора зростають пропорційно квадрату струму. Аналіз приведеної формули показує, що коефіцієнт корисної дії трансформатора має найбільше значення при рівності електричних втрат потужності в обмотках і втрат потужності в магнітопроводі трансформатора (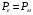 ). При дальшому зростанні навантаження трансформатора втратами в магнітопроводі можна знехтувати із-за їх відносно невеликого значення у порівнянні з досить великими електричними втратами потужності в обмотках трансформатора. Аналіз показує, що при цих умовах коефіцієнт корисної дії трансформатора зі збільшенням струму навантаження понад номінальне буде трохи знижуватися, що видно з рис. 8.
). При дальшому зростанні навантаження трансформатора втратами в магнітопроводі можна знехтувати із-за їх відносно невеликого значення у порівнянні з досить великими електричними втратами потужності в обмотках трансформатора. Аналіз показує, що при цих умовах коефіцієнт корисної дії трансформатора зі збільшенням струму навантаження понад номінальне буде трохи знижуватися, що видно з рис. 8.
Коефіцієнт корисної дії сучасних трансформаторів досить високий. Зі збільшенням номінальної потужності трансформатора коефіцієнт корисної дії росте, причому для потужних трансформаторів він досягає значень порядку 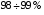

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ