Техническая механика
Задача 1
Дано:
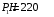 ,
,
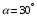 ,
,
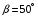 .
.
Найти: 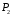 ,
, 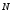 .
.

Рис. 1
Решение:
1. Решим задачу аналитически. Для этого рассмотрим равновесие шара 1. На него действует реакция N опорной поверхности А, перпендикулярная к этой поверхности; сила натяжения Т1 нити и вес Р1 шара 1 (рис. 2).

Рис. 2
Уравнения проекций всех сил, приложенных к шару 1, на оси координат имеют вид:
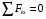 :
: 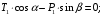 (1)
(1)
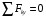 :
: 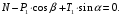 (2)
(2)
Из уравнения (1) находим силу натяжения Т1 нити:
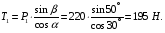
Тогда из уравнения (2) определим реакцию N опорной поверхности:
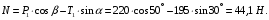
Теперь рассмотрим равновесие шара 2. На него действуют только две силы: сила натяжения Т2 нити и вес Р2 этого шара (рис. 3).

Рис. 3
Поскольку в блоке Д трение отсутствует, получаем
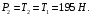
2. Решим задачу графически. Строим силовой треугольник для шара 1. Сумма векторов сил, приложенных к телу, которое находится в равновесии, равна нулю, следовательно, треугольник, составленный из 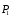 ,
, 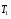 и
и 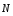 должен быть замкнут (рис. 4).
должен быть замкнут (рис. 4).

Рис. 4
Определим длины сторон силового треугольника по теореме синусов:
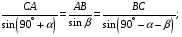
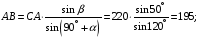
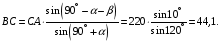
Тогда искомые силы равны:
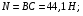
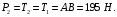
Задача 2
Дано:
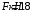 ,
,
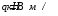 ,
,
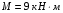 ,
,
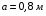 ,
,
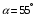 .
.
Найти: 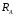 ,
, 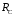 .
.

Рис. 5
Решение
1. Рассмотрим равновесие балки АВ. На неё действует равнодействующая Q распределённой на отрезке ЕК нагрузки интенсивности q, приложенная в середине этого отрезка; составляющие XA и YA реакции неподвижного шарнира А; реакция RС стержня ВС, направленная вдоль этого стержня; нагрузка F, приложенная в точке К под углом 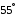 ; пара сил с моментом М (рис. 6).
; пара сил с моментом М (рис. 6).

Рис. 6
2. Равнодействующая распределенной нагрузки равна:
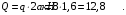
3. Записываем уравнение моментов сил, приложенных к балке АВ, относительно точки А:
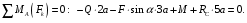 (3)
(3)
4. Уравнения проекций всех сил на оси координат имеют вид:
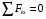 :
: 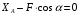 , (4)
, (4)
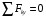 :
: 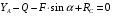 , (5)
, (5)
Из уравнения (3) находим реакцию RС стержня ВС:
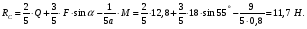
По уравнению (4) вычисляем составляющую XA реакции неподвижного шарнира А:
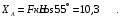
С учетом этого, из уравнения (5) имеем:
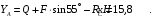
Тогда реакция неподвижного шарнира А равна:
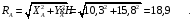
Задача 3
Дано:
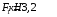 ,
,
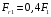 ,
,
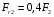 .
.
Найти: 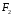 ,
, 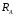 ,
, 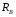 .
.

Рис. 7
Решение
Рассмотрим равновесие вала АВ. Силовая схема приведена на рис. 8.
Уравнения проекций сил на координатные оси имеют вид:
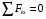 :
: 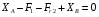 , (6)
, (6)
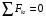 :
: 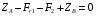 , (7)
, (7)

Рис. 8
Линии действия сил F1, Fr2 XA и XB параллельны оси х, а линия действия силы ZA пересекает ось х, поэтому их моменты относительно этой оси равны нулю.
Аналогично линии действия сил Fr1, Fr2 XA, XB, ZA и ZB пересекают ось у, поэтому их моменты относительно этой оси также равны нулю.
Относительно оси z расположены параллельно линии действия сил ZА, ZB Fr1 и F2, а пересекает ось z линия действия силы XA, поэтому моменты этих сил относительно оси z равны нулю.
Записываем уравнения моментов всех сил системы относительно трёх осей:
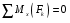 :
: 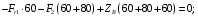 (8)
(8)
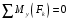 :
: 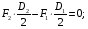 (9)
(9)
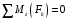 :
: 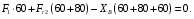 (10)
(10)
Из уравнения (4) получаем, что
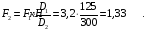
Из уравнения (3) находим вертикальную составляющую реакции в точке В:
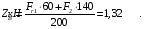
По уравнению (10), с учетом 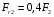 , рассчитываем горизонтальную составляющую реакции в точке В:
, рассчитываем горизонтальную составляющую реакции в точке В:
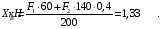
Из уравнения (6) определяем горизонтальную составляющую реакции в точке А:
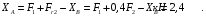
Из уравнения (7) имеем
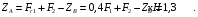
Тогда реакции опор вала в точках А и В соответственно равны:
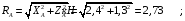
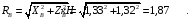
Задача 4
Дано:
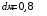 ,
,
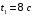 ,
,
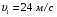 ,
,
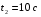 ,
,
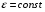 .
.
Найти: 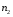 ,
, 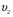 ,
, 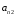 ,
, 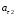 .
.
Решение
1. Поскольку маховик вращается равноускоренно, то точки на ободе маховика вращаются по закону:
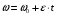 (11)
(11)
По условию задачи маховик в начальный момент находился в покое, следовательно, 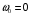 и уравнение (11) можно переписать как
и уравнение (11) можно переписать как
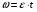 (12)
(12)
2. Определяем угловую скорость вращения точек обода маховика в момент времени 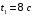 :
:
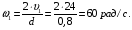
3. Находим угловое ускорение вращения маховика из уравнения (12):
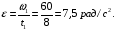
4. Вычисляем угловую скорость вращения точек обода маховика в момент времени 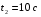 :
:
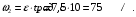
5. Тогда частота вращения маховика в момент времени 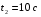 равна:
равна:
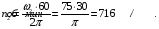
6. По формуле Эйлера находим скорость точек обода маховика в момент времени  :
:
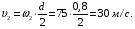
7. Определяем нормальное ускорение точек обода маховика в момент времени  :
:
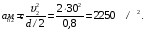
8. Находим касательное ускорение точек обода маховика в момент времени 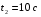 :
:
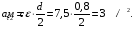
Задача 5
Дано:
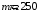 ,
, 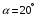 ,
, 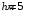 ,
, 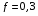 ,
,
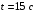 ,
, 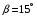 . Найти:
. Найти: 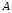 ,
, 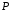 .
.

Рис. 9
Решение
1. Работа силы F определяется по формуле:
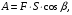 (13)
(13)
где 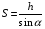 – перемещение груза.
– перемещение груза.
2. По условию задачи груз перемещается с постоянной скоростью, поэтому ускорение груза 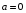 .
.

Рис. 10
3. Выбираем систему координат, направляя ось х вдоль линии движения груза. Записываем уравнения движения груза под действием сил (рис. 10):
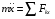 :
: 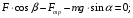 (14)
(14)
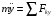 :
: 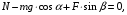 (15)
(15)
где 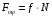 – сила трения скольжения.
– сила трения скольжения.
Выражаем из уравнения (14) реакцию 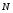 наклонной плоскости
наклонной плоскости
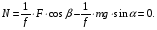
и подставляем в уравнение (15), получаем
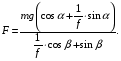
Тогда работа силы F равна
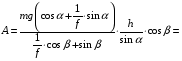
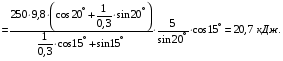
4. Мощность, развиваемая за время перемещения 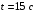 , определяется по формуле:
, определяется по формуле:
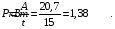

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ