МКОУ ООШ п. Пудожгорский

Урок

по физике

на тему «Великий ученый древнего мира – АРХИМЕД

и его закон»

Обучающегося 7 класса

МКОУ ООШ п. Пудожгорский

Ермолаева Александра

Учитель: Ошутинская Н. Б.

п. Пудожгорский

2010 год

Оглавление:

I. Введение 3

II. ОСНОВНАЯ ЧАСТЬ 4

II.1. Теоретическая часть 4

II.1.1. Об Архимеде 4

II.1.2. Закон Архимеда 8

II.1.3. От чего зависит выталкивающая сила 10

II.1.4. Примеры проявления закона Архимеда в природе 11

II.2. Практическая часть 15

II.2.1. Доказательство существования архимедовой силы 15

II.2.2. Расчет архимедовой силы 15

II.2.3. Условия плавания тел 15

II.2.3.1. Сравнение силы тяжести и архимедовой силы 17

II.2.3.2. Сравнение плотностей жидкости и тела 17

II.2.3.3. Сравнение архимедовой силы, действующей на тело в разных по плотности жидкостях 18

II.2.3.4. Сравнение архимедовой силы у двух тел, разных по плотности и одинаковых по объему 19

II.2.3.5. Сравнение архимедовой силы у двух тел, одинаковых по плотности и разных по объему 19

III. Вывод 20

IV. Список используемых источников и литературы 21

I. Введение

Тема моего реферата «Великий ученый древнего мира – Архимед и его закон».

Цель работы: изучение закона Архимеда, выяснение условий и особенностей плавания тел, проверка их на опытах.

Задачи:

1. Подобрать и изучить литературу по теме.

2. Рассказать об истории открытия закона Архимеда.

3. Доказать существование архимедовой силы.

4. Рассчитать архимедову силу, действующую на предметы.

5. Проверить условия плавания тел на опытах.

II. ОСНОВНАЯ ЧАСТЬ

II.1. Теоретическая часть

II.1.1. Об Архимеде

Архимед родился в греческом городе Сиракузы в 287 году до н. э., где и прожил почти всю свою жизнь, и там же занимался научной деятельностью. Учился сначала у своего отца, астронома и математика Фидия, потом в Александрии, где правители Египта собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку. Здесь, в Александрии, Архимед познакомился с учени­ками Эвклида, с которыми всю жизнь поддержи­вал оживленную переписку. Здесь же он усиленно изучал труды Демокрита, Евдокса и других ученых.

После учебы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца, придворного астронома.

В теоретическом отношении труд этого великого ученого был ослепляюще многогранным. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики. Он был также изобретательным инженером, который использовал свой талант для решения ряда практических проблем.

Архимед – автор ряда необыкновенно глубоких и оригинальных работ по математике.

До нас дошло тринадцать трактатов Архимеда. В самом знаменитом из них - "О шаре и цилиндре" (в двух книгах) Архимед устанавливает, что площадь поверхности шара в 4 раза больше площади наибольшего его сечения. Работы Архимеда состоят из расчетов площадей фигур, ограниченных кривыми, и объемов тел, ограниченных произвольными плоскостями — поэ­тому Архимед может по справедливости считаться отцом интегрального исчисления, возникшего на два тысячелетия позже.

Говорят, будто важней­шим своим открытием Архимед считал доказа­тельство, что объем шара и описанного вокруг не­го цилиндра относятся между собой как 2:3. Архимед просил своих друзей поместить это до­казательство на его могильной плите.

Архимед пы­тался также решить проблему квадратуры круга и до­стиг в этом выдающихся результатов, объединив их в труд «Об измерении круга»:

1. Площадь круга равна площади прямоугольно­го треугольника с катетами, равными длине и радиусу окружности (πr²).

2. Площадь круга так относится к площади опи­санного вокруг него квадрата, как 11:14.

3. Отношение длины окружности к диаметру больше и меньше .

Архимед впервые вычислил число «пи» — отношение длины окружности к диаметру — и доказал, что оно одинаково для любого круга.

Архимед нашел также сумму бес­конечной геометрической прогрессии со знаменателем . В математике это был первый пример бесконеч­ного ряда.

При исследовании одной задачи, сводящейся к кубическому уравнению, Архимед выяснил роль характеристики, которая позже получила название дискриминанта.

Архимеду принадлежит формула для определения площади треугольника через три его стороны (неправильно именуемая формулой Герона).

Большую роль в развитии мате­матики сыграло его сочинение «Псаммит» - «О числе песчинок», в котором он показывает, как с по­мощью существовавшей системы счисления можно выражать сколь угодно большие числа. В качестве повода для своих рассуждений он использует задачу о подсчете коли­чества песчинок внутри видимой Все­ленной. Тем самым было опроверг­нуто существовавшее тогда мнение о наличии таинственных «самых больших чисел». Мы до сих пор пользуемся придуманной Архимедом системой наименования целых чисел.

Перечисленные научные находки — это только небольшая часть творчества Архимеда. Его усердно переводили и комментировали арабы, а по­том западноевропейские ученые.

В физике Архимед ввел понятие центра тяжести, установил научные принципы статики и гидростатики, дал образцы применения математических методов в физических исследованиях. Основные положения статики сформулированы в сочинении "О равновесии плоских фигур". Архимед рассматривает сложение параллельных сил, определяет понятие центра тяжести для различных фигур, дает вывод закона рычага. Знаменитый закон гидростатики, вошедший в науку с его именем (закон Архимеда), сформулирован в трактате "О плавающих телах".

Ему при­писывают известное выражение: „дайте мне точку опоры, и я сдвину землю". По-видимому, оно было высказано в связи со спуском корабля «Сиракосия» на воду. Рабочие были не в силах сдвинуть с места этот корабль. Им помог Архимед, создавший систе­му блоков (полиспаст), при помощи которой один человек, сам царь, совершил эту работу.

Любопытен отзыв Цицерона, великого оратора древности, увидевшего «архимедову сферу» — модель, механический прибор, на котором можно было наблюдать движения планет, фазы Луны, солнечные и лунные затмения: «Этот сицилиец обладал гением, которого, казалось бы, человеческая природа не может достигнуть».

Плутарх восславил Архимеда за его участие в за­щите родного города Сиракуз от римлян. Именно при осаде Си­ракуз, богатого торгового города на острове Сицилия, с осо­бой силой проявился инженерный гений Архимеда.

Воины римского консула Марцелла были надолго задержаны у стен го­рода невиданными машинами: мощ­ные катапульты прицельно стреляли каменными глыбами, в бойницах бы­ли установлены метательные маши­ны, выбрасывающие грады ядер, бе­реговые краны поворачивались за пределы стен и забрасывали кораб­ли противника каменными и свин­цовыми глыбами, крючья подхваты­вали корабли и бросали их вниз с большой высоты, системы вогну­тых зеркал поджигали флотилию. В «Ис­тории Марцелла»

Плутарх описыва­ет ужас, царивший в рядах римских воинов: «Как только они замечали, что из-за крепостной стены показы­вается веревка или бревно, они кричали: “Вот, вот оно!”– и, думая, что Архимед хочет направить на них какую-нибудь машину, ударялись в бегство». Плутарх утверждал, что Архимед "один был душой обороны, приводил все в движение и управлял защитой".

Несколько месяцев длилась осада Сиракуз, и лишь благодаря предателям, открывшим ворота, римляне, наконец, смогли ворваться в город. “Немало примеров гнусной злобы и гнусной алчности можно было бы припомнить, – но самый знаменитый между ними – убийство Архимеда. Среди дикого смятения, под крики и топот озверевших солдат, Архимед спокойно размышлял, рассматривая начерченные на песке фигуры, и какой-то грабитель заколол его мечом, даже не подозревая, кто это”.

Последние его слова, обращенные к своему убийце, содержа­ли просьбу не уничтожать чертеж, над ко­торым он размышлял.

Сто лет спустя Цицерон, посетивший Сицилию, на­шел могилу Архимеда по шару, вписанному в ци­линдр, изображенному на могильном камне.

Архимед был человеком, страстно увлеченным механикой. Он проверил и создал теорию пяти механизмов, известных в его время и именуемых «простые механизмы». Это — рычаг, клин, блок, бесконечный винт и лебедка. Именно Архимеду часто приписывают изобретение бесконечного винта, но возможно, что он лишь усовершенствовал гидравлический винт, который служил египтянам при осушении болот и был применен при осушении залитых Нилом земель. Впоследствии эти механизмы широко применялись в разных странах мира.

И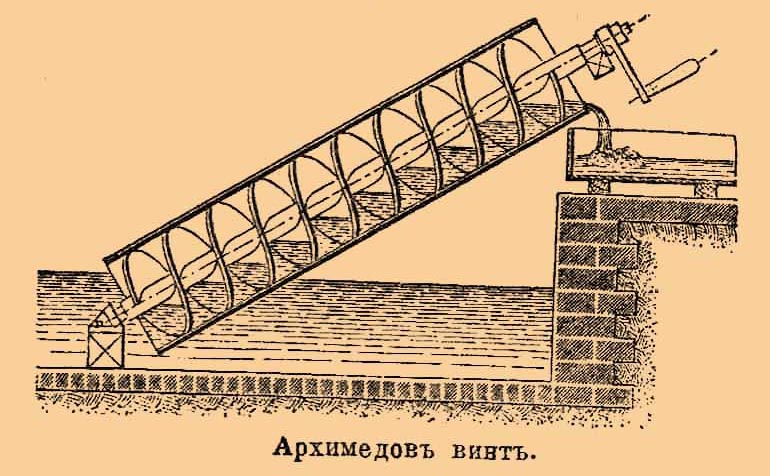нтересно, что усовершенствованный вариант водоподъемной машины так называемый «архимедов винт», который явился прообразом корабельных, а также воздушных винтов, можно было встретить в начале XX века в монастыре, находившемся на Валааме. Сегодня же архимедов винт используется, к примеру, в обыкновенной мясорубке.

Изобретение бесконечного винта привело его к другому важному изобретению, пусть даже оно и стало обычным, — к изобретению болта, сконструированного из винта и гайки.

Любопытно, что, завоевав Сиракузы, римляне так и не стали обладателями трудов Архимеда. Только через много веков они были обнаружены европейскими учеными.

Архимед оставил многочисленных учеников. На новый путь, открытый им, устремилось целое поколение последователей, энтузиастов, которые горели желанием, как и учитель, доказать свои знания конкретными завоеваниями.

II.1.2. Закон Архимеда

По преданию, царь Гиерон поручил Архимеду проверить, из чистого ли золота сделана его корона или же ювелир присвоил часть золота, сплавив его с серебром. Размышляя над этой задачей, Архимед как-то зашел в баню и там, погрузившись в ванну, заметил, что количество воды, переливающейся через край, равно количеству воды, вытесненной его телом. Это наблюдение подсказало Архимеду решение задачи о короне, и он, не медля ни секунды, выскочил из ванны и, как был нагой, бросился домой, крича во весь голос о своем открытии: «Эврика! Эврика!» (греч. «Нашел! Нашел!»)».

Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменится.

Чтобы понять природу силы, действующей со стороны жидкости на погруженное тело, достаточно рассмотреть простой пример (рис. 1).

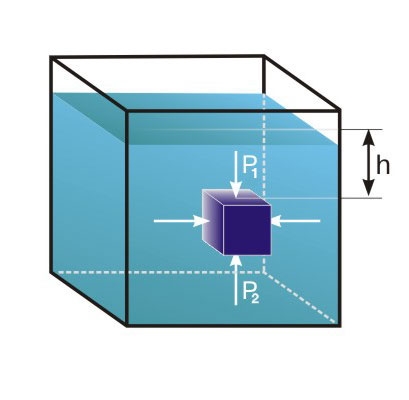
Рис. 1.

Кубик погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля.

Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и нижнюю грани. Так как давление на глубине больше, чем у поверхности жидкости и , а, то >. Так как силы F₂ и F₁ направлены в противоположные стороны, то их равнодействующая равна разности F₂ – F₁ и направлена в сторону большей силы, то есть вверх. Эта равнодействующая и является архимедовой силой, то есть силой, выталкивающей тело из жидкости.

Закон Архимеда (фрагмент из книги Ефима Ефимовского “След колесницы”)

Жил в Сиракузах мудрец Архимед.
Был другом царя Гиерона.
Какой для царя самый важный предмет?
Вы все догадались: корона!
Захотелось Гиерону сделать новую корону.
Золота отмерил строго,
Взял не мало и не много, -
Сколько нужно, в самый раз,
Ювелиру дал заказ.
Через месяц Гиерону ювелир принес корону,
И царю узнать охота: честно ль сделана работа?
- Вот корона, Архимед, золотая или нет?
И задумался ученый:
Как узнать состав короны?
И однажды, в ванне моясь,
Погрузился он по пояс.
На пол вылилась вода: догадался он тогда,
И помчался к Гиерону не обут и не одет...
- Эврика! Раскрыл секрет!
Пусть весы сюда несут и с собой большой сосуд.
На весы кладем корону и теперь, такой же ровно,
Ищем слиток золотой.
Мы теперь корону нашу опускаем в эту чашу.
Гиерон! Смотри сюда -
В чаше поднялась вода!
Ставлю черточку по краю,
А корону вынимаю.
В воду золото опустим.
В воду золото допустим...
Поднялась опять вода. Метку ставлю я.
Куда?
Ну, конечно же, по краю.
- Ничего не понимаю.
Лишь две черточки я вижу.
Эта выше, эта - ниже.
- Но какой же вывод главный?
Равный вес. Объем - не равный!
Понимаешь, Гиерон, я сейчас открыл закон.
Тот закон совсем простой:
Тело вытеснит...
- Постой!
Говоришь: объем неравный?
Мастер мой мошенник явный!
За фальшивую корону он ответит по закону!
А ты за разгадку получишь дары.

Два обстоятельства важны в этой легенде.

1. Архимед нашел способ измерить объем твердого тела сложной формы.
2. Он сопоставил веса различных веществ не друг с другом, а с весом воды, т.е. впервые обратил внимание на свойство физических тел, которое мы называем плотностью, открыл гидростатический способ взвешивания.

ВЫВОД. Закон Архимеда формулируется таким образом: тело, находящееся в жидкости (или газе), теряет в своем весе столько, сколько весит жидкость (или газ) в объеме, вытесненном телом.

II.1.3. От чего зависит выталкивающая сила

Поведение тела, находящегося в жидкости, зависит от соотношения между модулями силы тяжести F_т и архимедовой силы F_A, которые действуют на это тело. Возможны следующие три случая:

1. F_т > F_A – тело тонет;

2. F_т = F_A – тело плавает в жидкости;

3. F_т < F_A – тело всплывает до тех пор, пока не начнет плавать на поверхности жидкости.

Также поведение тела, находящегося в жидкости, зависит от соотношения плотностей тела и жидкости. Следовательно, для определения поведения тела в жидкости, можно сравнить плотности тела и жидкости. В данном случае возможны также три ситуации:

1. ρ_тела > ρ_{жидкости} – тело тонет

2. ρ_тела = ρ_{жидкости} – тело плавает

3. ρ_тела < ρ_{жидкости} – тело всплывает.

Приведем примеры.

Плотность железа – 7800 кг/м³, плотность воды – 1000 кг/м³. Значит, кусок железа будет тонуть в воде. Плотность льда – 900 кг/м³, плотность воды – 1000 кг/м³, поэтому лед в воде не тонет, а если его бросить в воду, то он начнет всплывать, и будет плавать на поверхности.

II.1.4. Примеры проявления закона Архимеда в природе

         Открытие основного закона гидростатики – одно из крупнейших завоеваний античной науки. Чтобы оценить значение открытия, рассмотрим примеры проявления и использования этого закона в природе, широко известного как закон Архимеда.

        Воды южных морей имеют более высокую соленость и плотность, чем воды арктического бассейна. Поэтому в Арктике нередки случаи, когда воды теплых течений опускаются под холодные воды северных широт. Например, в районе севернее Шпицбергена теплое южное течение опускается под холодные воды Ледовитого океана. Подобным же образом теплое течение Жаннетты, выходя из Берингова пролива, проходит под водами Арктики и выходит на поверхность лишь у берегов Северной Америки. Различная соленость вод имеет большое значение для возникновения течений и в южных широтах. В Мраморном море вода более соленая и быстрее испаряется, чем в Черном. Поэтому через Босфор в придонных слоях вода протекает из Мраморного моря в Черное, в поверхностных же слоях имеет место противоположное течение.

        Подземные реки могут иметь выход не только на земную поверхность, но и на дно моря. Будучи более легкими, воды этих рек в неглубоком море могут подниматься до его поверхности, практически не смешиваясь с соленой водой. Подобные выходы пресных вод в открытом море имеются вблизи Марокканского побережья Атлантического океана (у Агадира) и в Коринфском заливе Ионического моря – вблизи Коринфа.

        Поскольку средняя плотность тела рыб близка к плотности воды, их вес вблизи основных горизонтов жизнедеятельности достаточно хорошо уравновешивается выталкивающей силой по закону Архимеда. Благодаря ритмичной работе мышц рыба может отталкиваться от воды и таким образом перемещаться. При этом по ее телу в направлении от головы к хвосту с возрастающей амплитудой пробегает плоская или винтообразная упругая волна. Скорость распространения этой волны превышает быстроту перемещения рыбы. За счет ритмичного отталкивания от воды при распространении по телу упругой волны и осуществляется плавание рыб. К помощи плавников рыбы прибегают только для поддержания равновесия и при медленных перемещениях.

        Такие обитатели морей, как осьминог, каракатица, моллюск сальпа, при перемещении используют принцип реактивного движения – они втягивают воду в специальные мускулистые мешки своего тела, а затем выталкивают ее наружу. Благодаря этому животные получают возможность перемещаться в направлении, противоположном выбрасываемой струе. А веслоногие, например черепахи, плавают, отталкиваясь от воды ногами.

        Мелкие рыбы обычно движутся стаями. К этому их принуждает то обстоятельство, что при увеличении скорости движения близко расположенных тел по закону Бернулли понижается давление в пространстве между ними. Давление между каждыми двумя соседними рыбами в рыбьем косяке будет меньше, чем в среде, не возмущенной движением рыбьей стаи. В этом случае рыбы будут испытывать небольшую прижимающую их друг к другу силу и двигаться вместе. Если бы рыбы в косяке не подчинялись действию гидродинамических сил, они затрачивали бы больше энергии для своего перемещения.

        В Средиземном море, у берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.

        Живущий в тропических морях моллюск наутилус может быстро всплывать и вновь опускаться на дно. Моллюск этот живет в закрученной спиралью раковине. Когда ему нужно подняться или опуститься, он изменяет объем внутренних полостей в своем организме.

        У широко распространенного в Европе водяного паука, обитающего в стоячих или слабо проточных водах, поверхность брюшка не смачивается водой. Уходя в глубину, он уносит с собой приставшую к брюшку воздушную оболочку, которая придает ему запас плавучести и помогает возвращению на поверхность.

        Произрастающий в дельте Волги вблизи Астрахани чилим (водяной орех) после цветения дает под водой тяжелые плоды. Эти плоды настолько тяжелы, что вполне могут увлечь на дно все растение. Однако в это время у чилима, растущего в глубокой воде, на черешках листьев возникают вздутия, придающие ему необходимую подъемную силу, и он не тонет.

        Известно, что наибольшие по размерам животные нашей планеты живут в воде. Закон Архимеда способствует тому, чтобы они не были раздавлены весом своего тела. В наше время самым крупным животным является кит, длина его может достигать 30 м. В мезозое крупнейшими были динозавры и среди них атлантозавр, длина тела которого составляла около 60 м.

        Так как тела обитателей морей и рек содержат в своем составе много воды, давление в организме этих животных и в окружающей среде легко выравнивается. У рыб с плавательным пузырем такое уравнивание происходит лишь в сферах их постоянной жизнедеятельности. При быстром подъеме из области больших глубин на поверхность водоема плавательный пузырь рыб под действием высокого внутреннего давления выдавливается наружу, что приводит к их гибели.

        В Мертвом море за счет большого количества растворенных солей (более 27% по весу) плотность воды достигает 1,16 г/см³. Купаясь в этом море, человек очень мало погружается в воду, находясь как бы на поверхности, поскольку средняя плотность тела человека меньше плотности воды. В нашей стране еще более высокая плотность воды наблюдается в заливе Кара-Богаз-Гол на Каспии и в озере Эльтон.

        Для жизни под водой человек совершенно не приспособлен. На глубине 20 м под действием внешнего давления у него могут лопнуть барабанные перепонки. Опуститься же на глубину более 70 м без специального костюма человеку совершенно невозможно. (Правда, натренированные пловцы на очень короткое время опускаются под воду на глубину до 51 м).

        В человеческом организме в полости живота давление немного превышает атмосферное, в полости груди, наоборот, меньше атмосферного. Если человек, находясь неглубоко под водой, попытается дышать через узкую трубочку (тростинку или соломинку), то он может непродолжительное время это делать только при толщине находящегося над ним слоя воды менее 1 м. Дополнительное давление на человеческий организм столба воды в 1 м и более быстро приводит к полному прекращению дыхания и кровообращения. При этом кровь переполняет сердце, а брюшная полость и ноги почти совершенно обескровливаются. В процессе же ныряния жизнедеятельность человека существенным образом не нарушается, поскольку в этом случае он набирает в легкие дополнительное количество воздуха, которое помогает ему уравновешивать давление воды на его организм.

        Известный русский адмирал М.П. Лазарев неоднократно показывал матросам во время плаваний следующий любопытный опыт с бутылкой. С помощью свинцового груза порожнюю закупоренную бутылку матросы опускали под воду на глубину до 430 м. После ее подъема на палубу они с удивлением убеждались, что бутылка заполнена глубинной водой и плотно закрыта пробкой, причем верх и низ пробки поменялись местами. Это происходило за счет давления воды, которое, в соответствии с законами гидродинамики, на глубине 430 м имеет вполне достаточную для этого величину. Опыт Лазарева представляет собой яркую демонстрацию действия давления воды на больших глубинах. Это позволяет лучше понять действие давления воды и на человеческий организм.

        Многим, наверное, не раз приходилось наблюдать ледоход на реках. Еще более грандиозное зрелище представляют собой айсберги – «плавучие ледяные горы» больших размеров. Айсберги – это массы материкового льда, оторвавшиеся от ледника или ледового барьера и плавающие в полярных морях и прилегающих к ним акваториях.

        Средняя высота надводной части айсберга нередко достигает 50...70 м, максимальное ее значение приближается к 450 м. Наибольшая длина подводной части может доходить до 130 км. Объем надводной части айсберга составляет небольшую часть его полного объема.

        Перемещаясь в более теплые воды, айсберг оплавляется снизу, в результате чего центр тяжести его перемещается выше центра, к которому приложено выталкивающее действие воды. Такой айсберг теряет равновесие и с шумом переворачивается.

        При спокойном море и отсутствии ветра айсберг с подтаявшей нижней частью начинает раскачиваться, что является признаком предстоящего переворачивания. Когда айсберг находится в состоянии неустойчивого равновесия, даже работа машин находящегося поблизости корабля может дать толчок к переворачиванию.

        Таяние айсбергов на южной границе северных морей вызывает некоторое понижение солености воды. В этом же районе в процессе таяния айсберги сбрасывают на дно морей захваченные ими части морен, а иногда и довольно крупные куски скал.

        В средней полосе Советского Союза имеются следы подобной деятельности айсбергов, относящиеся к периоду, когда территория нашей страны была дном моря. Аналогично происходит вынос окатанной гальки на дно арктического бассейна. Примерзая ко льду у берегов, галька вместе с льдинами уносится впоследствии в океан и опускается на его дно после таяния льда.

        В некоторых реках при быстром течении за счет интенсивного перемешивания воды происходит переохлаждение отдельных участков дна. При этом переохлажденный участок дна покрывается льдом внутриводного и отчасти поверхностного происхождения. Иногда донный лед занимает значительную часть сечения реки. Тогда река выходит из берегов, и становится возможным наводнение.

        Так как подъемная сила льда пропорциональна его объему, а сила сцепления с ложем реки пропорциональна поверхности, то при отложении достаточно большого количества льда на дне он может преодолеть сцепление с ложем и всплыть на поверхность. Поднявшаяся на поверхность губчатая масса донного льда обычно содержит различные включения: камни, песок, а иногда и затонувшие якоря вместе с якорными цепями. Донный лед может возникать не только на реках, но и в неглубоких местах морей и озер (вблизи берегов), где переохлаждение достигает дна водоема. В этом случае всплывающий лед поднимает на поверхность придонные водоросли.

        Искусно используют закон Архимеда подводники. Если подводная лодка плывет между слоями воды с разной температурой, ее балласт подбирают таким образом, чтобы обеспечить небольшую перегрузку для теплого слоя и недогрузку для холодного. В этом случае лодка лежит на холодном слое, не нуждаясь в специальных мерах для поддержания равновесия. Для батискафа с небольшой отрицательной плавучестью слой более плотной воды может играть роль уравновешивающего «жидкого грунта».

        При переходе подводной лодки из морских глубин в устье реки, подводники тщательно следят за расстоянием между лодкой и дном, так как в пресной воде выталкивающая сила Архимеда меньше, чем в морской, и при недосмотре со стороны экипажа лодка может сесть на илистый грунт речного устья.

        Очень большое значение закон Архимеда имеет в технике бурения. Буровая колонна для бурения глубоких скважин уже на глубине 5 км в воздухе имела бы вес 226 тонн. Однако в промывочной жидкости плотностью 2 г/см³ в соответствии с законом Архимеда вес буровой колонны будет сильно уменьшен. Алюминиевые трубы «теряют» в весе в этих условиях до 50%. Подбором промывочной жидкости можно намного уменьшить вес буровой колонны. Это в огромной степени способствует успеху бурения.

        Используя законы гидростатики, человек все полнее познает условия жизни в водной среде и все больше подчиняет водную стихию своей власти.

II.2. Практическая часть

II.2.1. Доказательство существования архимедовой силы

Проведем эксперимент: возьмем цилиндр, подвешенный к динамометру, измерим вес этого цилиндра. Погрузим его в сосуд с водой. Снова взвесим. Мы заметили, что вес цилиндра стал меньше.

Повторим эксперимент с другим телом – связкой ключей. Вес связки, погруженной в воду, опять стал меньше.

Вывод: на всякое тело, погруженное в жидкость, действует выталкивающая сила, называемая архимедовой силой.

II.2.2. Расчет архимедовой силы

Рассчитаем выталкивающую силу.

Для этого измерим вес тела в воздухе, затем измерим вес этого же тела, но полностью погруженного в воду. Разность этих сил и будет значением архимедовой силы.

F_А = P в возд. – P в воде.

Иначе, архимедову силу можно вычислить, зная плотность жидкости и объем тела, погруженного в эту жидкость, по формуле:

F_А = g ρ_жV_т

II.2.3. Условия плавания тел

I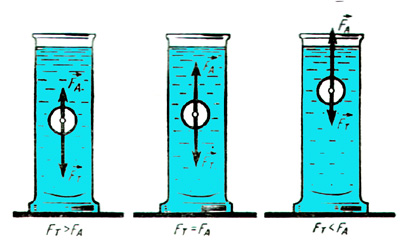I.2.3.1. Сравнение силы тяжести и архимедовой силы

Проведем эксперимент.

Возьмем тело – пузырек с некоторым количеством песка. Определим силу тяжести и архимедову силу, действующую на это тело. Сравним их. Мы видим, что, если:

F_т > F_A – тело тонет;

F_т = F_A – тело плавает в жидкости;

F_т < F_A – тело всплывает

Вывод: поведение тела, находящегося в жидкости, зависит от соотношения между модулями силы тяжести F_т и архимедовой силы F_A, которые действуют на это тело.

II.2.3.2. Сравнение плотностей жидкости и тела

Проведем еще один эксперимент. Возьмем тела, плотности которых меньше или больше плотности воды. Погрузим их в воду. Мы увидим, что «тела, которые тяжелее жидкости, будучи опущены в неё, погружаются всё глубже, пока не достигают дна, и, пребывая в жидкости, теряют в своём весе столько, сколько весит жидкость, взятая в объёме тел», – как говорил Архимед.

Вывод: поведение тела, находящегося в жидкости, зависит от соотношения плотностей тела и жидкости.

Это свойство не раз встречалось в произведениях русских и советских писателей и поэтов.

Н.А. Некрасов. “Дедушка Мазай и зайцы”

…Мимо бревно суковатое плыло,
Сидя, и стоя, и лежа пластом,
Зайцев с десяток спасалось на нем.
“Взял бы я вас — да потопите лодку!”
Жаль их, однако, да жаль и находку —
Я зацепился багром за сучок
И за собою бревно поволок…

II.2.3.3. Сравнение архимедовой силы, действующей на тело в разных по плотности жидкостях

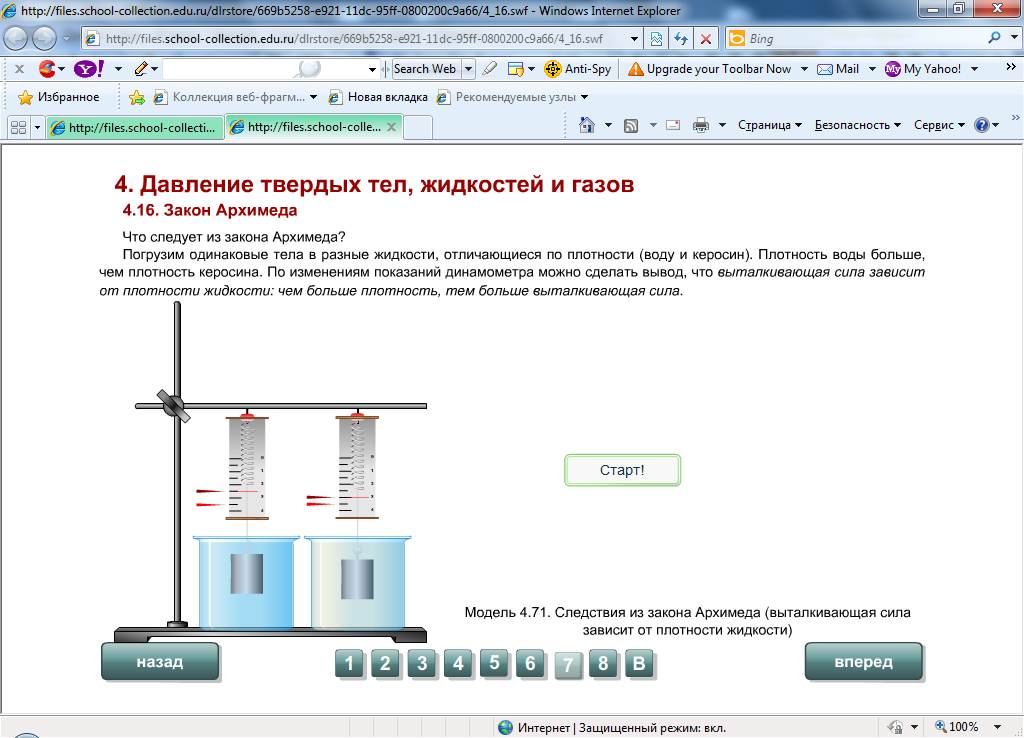
Проведем эксперимент: возьмем две жидкости, различных по плотности: шампунь и пресную воду, и кусок пластилина. Определим выталкивающую силу, действующую на пластилин со стороны каждой из жидкостей. Мы увидим, что архимедова сила оказалась разной: у жидкости с большей плотностью (шампуня) она больше, чем у жидкости с меньшей плотностью (пресной воды).

Вывод: архимедова сила зависит от плотности жидкости.

II.2.3.4. Сравнение архимедовой силы у двух тел, разных по плотности и одинаковых по объему

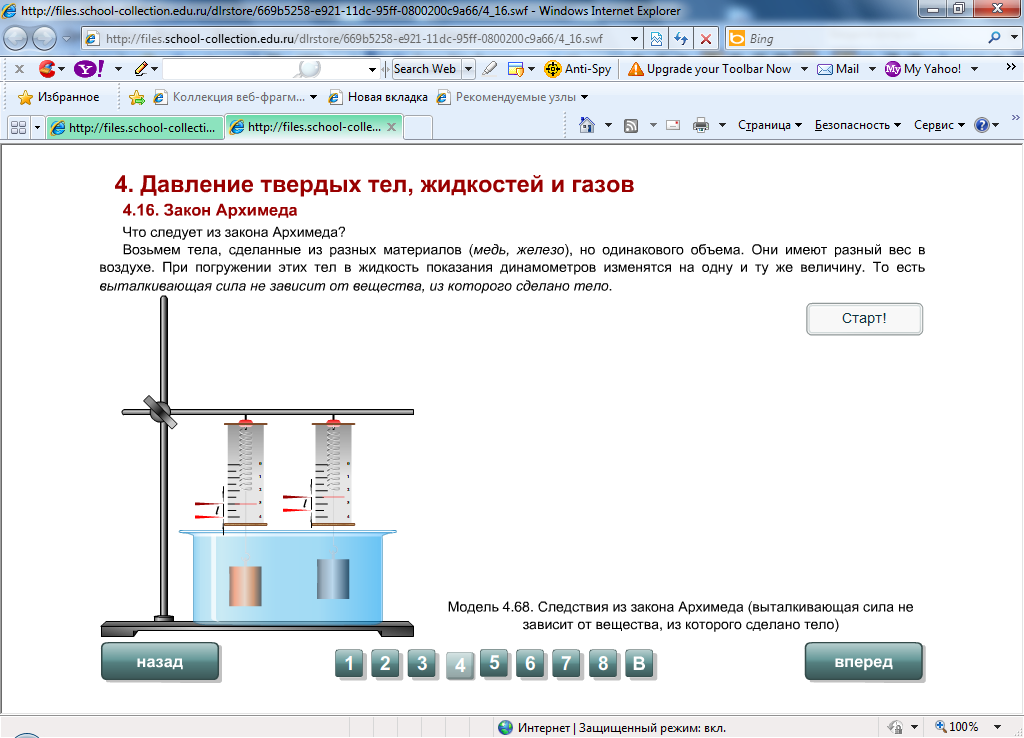
Проведем следующий эксперимент: возьмем два тела равного объема (цилиндры), но разной плотности. Определим выталкивающую силу, действующую на каждый цилиндр, полностью погруженный в воду. Архимедова сила оказалась одинаковой.

Вывод: архимедова сила не зависит от плотности тел.

II.2.3.5. Сравнение архимедовой силы у двух тел, одинаковых по плотности и разных по объему

П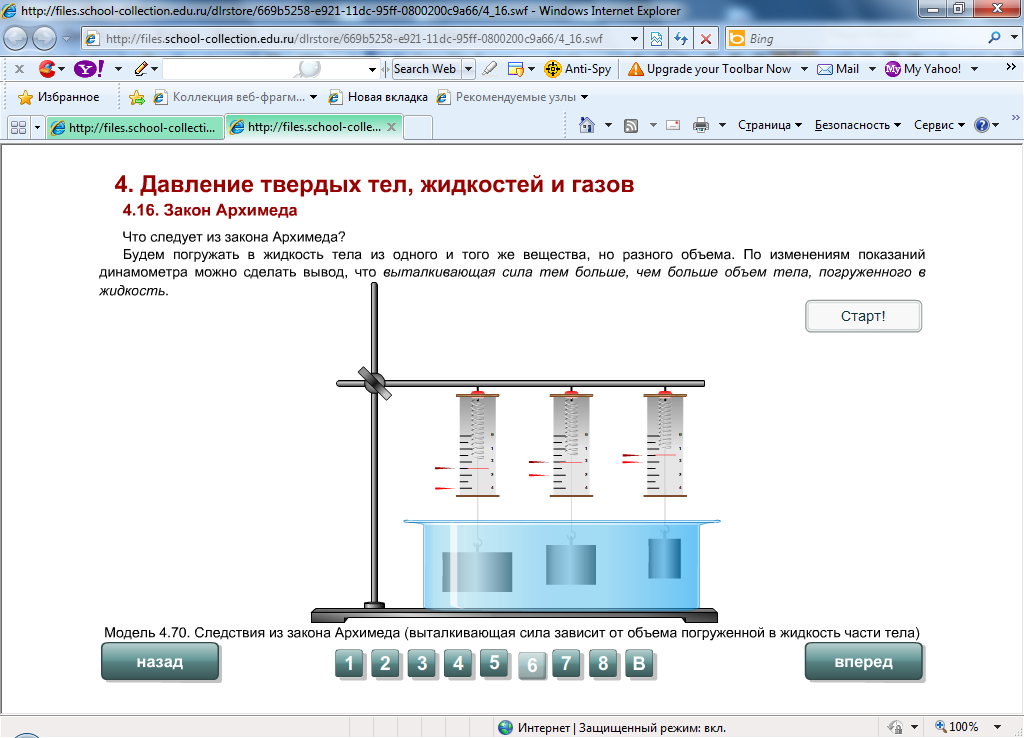роведем эксперимент: возьмем два тела одинаковой плотности (куски пластилина), но разного объема. Определим выталкивающую силу, действующую на каждый кусок пластилина, полностью погруженный в воду. Архимедова сила оказалась разной.

Вывод: архимедова сила зависит от объема тел.

III. Вывод

В своей работе я доказал существование и рассмотрел причины возникновения архимедовой силы (F_А) и показал, что она зависит от плотности жидкости и объема тела, погруженного в жидкость, и не зависит от плотности и формы тела, а также проверил условия и особенности плавания тел, то есть условия, при которых тело может плавать, тонуть или всплывать на поверхность жидкости.

На использовании действия архимедовой силы основано воздухоплавание (в газах) – полеты дирижаблей, аэростатов и т. п.; в воде – плавание судов и различных тел.

Я считаю, что если бы Архимед трагически не погиб, то он мог бы придумать и изобрести много новых механизмов и приспособлений и открыть новые законы.

Дмитрий Кедрин

Архимед (1941)

Нет, не всегда смешон и узок

Мудрец, глухой к делам земли:

Уже на рейде в Сиракузах

Стояли римлян корабли.

Над математиком курчавым

Солдат занес короткий нож,

А он на отмели песчаной

Окружность вписывал в чертеж.

Ах, если б смерть — лихую гостью —

Мне так же встретить повезло,

Как Архимед, чертивший тростью

В минуту гибели — число!

IV. Список используемых источников и литературы

1. Смышляев В.К. О математике и математиках. – Йошкар-Ола: Наука, 1977

2. Физика: Учеб. для 7 кл. общеобразоват. учреждений / С. В. Громов, Н. А. Родина. – М.: Просвещение, 2001.

3. Физика. 7 кл.: учеб. для общеобразоват. учреждений / А. В. Перышкин. – 11-е изд., стереотип. – М.: Дрофа, 2007.

4. Тихомирова С. А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002

5. Я познаю мир: Дет. энцикл.: Физика / Сост., худож. А. А. Леонович; Под общ. Ред. О. Г. Хинн. – М.: ТКО «АСТ», 1997.

6. Книга для чтения по физике: Учеб. пособие для учащихся 6-7 кл. сред. шк. / Сост. И. Г. Кириллова. – М.: Просвещение, 1986.

7. http://www.world-art.ru/lyric/lyric.php?id=13553

8. http://kref.ru/infoshpargalkipomatematike/129979/12.html

9. http://festival.1september.ru/articles/312841/

10. http://www.licey-reutov.ru/dlrstore/f053763a-767b-70d5-dcc7-716911ed31ad/0012076G.htm

11. http://homefizika.narod.ru/zakon_arhimeda/zakon_arkhimeda.htm

12. http://class-fizika.narod.ru/kit.htm

13. http://class-fizika.narod.ru/7_archim.htm

14. http://files.school-collection.edu.ru/dlrstore/669b5259-e921-11dc-95ff-0800200c9a66/4_17.swf

15. http://homefizika.narod.ru/zakon_arhimeda/plavanie_tel.htm – активная задача на плавание тел

16. http://homefizika.narod.ru/zakon_arhimeda/zadachi.htm – задачи по теме закон Архимеда

17. http://files.school-collection.edu.ru/dlrstore/669b525a-e921-11dc-95ff-0800200c9a66/4_18.swf – условия плавания тел с интерактивными примерами

18. http://files.school-collection.edu.ru/dlrstore/669b5258-e921-11dc-95ff-0800200c9a66/4_16.swf – закон Архимеда с интерактивными примерами

21