Рыбаков А.Б.

Заметки о механике автомобиля

0. Начнем с цитаты из одной замечательной книги, написанной более века назад.

«Когда система состоит из большого числа частей, то полное изучение её движения может оказаться очень сложным и даже невыполнимым. В таких случаях полезно, ранее подробного исследования движения частей системы, получить некоторое понятие об общем движении всей системы в совокупности» [1].

Именно этим мы и будем заниматься – принципиальными моментами механики «самодвижущихся экипажей» (как сказали бы в старину). Т.е. теми моментами, которые не связаны с конкретным устройством двигателя, трансмиссии и прочих вещей, милых сердцу каждого автомобилиста. Именно принципиальные моменты являются общими для «самодвижущихся экипажей» разных типов – автомобилей, локомотивов, тракторов, велосипедов и т.д. Лишь для удобства мы везде будем говорить именно об автомобиле.

Я не хочу здесь (как это делается в учебниках) сразу привести ответы на все вопросы (которые у читателя еще и не возникли). Я хочу, чтобы читатель прошел тот же путь, что и автор.

1.

Сначала надо заинтриговать читателя.

Недавно в одном из наших профессиональных журналов появилась статья о динамике автомобиля. Между делом, как о чем-то всем хорошо известном, в статье утверждалось, что если автомобиль проехал путь S, то «сила тяги» F_Т совершила работу A = F_ТS, и соответственно для мощности двигателя мы имеем известное соотношение: N = F_ТV.

В этом месте прошу читателя остановиться. Не читайте дальше! Проверьте себя. В этих (совершенно элементарных!) рассуждениях допущена грубая ошибка. Видите ли вы её?

2.

Разве можно что-то вычислять для некой силы, зная только её название, не выявив её конкретную природу и её свойства?

Что же это за «сила тяги»?

Читатель, возможно, помнит, что внутренние силы не могут привести систему в движение (к этой мысли мы еще вернемся). Значит, мы должны найти на эту роль внешнюю силу.

Автор знаменитейших «опорных конспектов» (забыл его фамилию) прикладывал «силу тяги» к мотору!! Поскольку у нас здесь не вечер юмора, оставим это без комментариев.

Если ваш автомобиль сломался и кто-то тянет вас на буксире, то сила тяги в этом случае – сила натяжения троса. И для работы этой силы справедлива приведенная выше формула.

Но нас-то интересует обычный режим движения.

И никакую другую силу, кроме силы трения шин ведущих колес о дорогу, на роль «силы тяги» не подобрать. На языке автомобилистов это «сила сцепления с дорогой». Заметим, что в нормальном режиме движения шина относительно дороги не проскальзывает, т.е. эта сила – сила трения покоя!

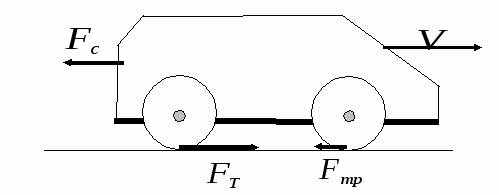
На рисунке показаны горизонтальные внешние силы, действующие на движущийся автомобиль с задними ведущими колесами. При равномерном движении сила тяги уравновешивает силу трения покоя между ведомыми колесами и дорогой и силу сопротивления воздуха :

(1)

а при движении с ускорением а

(2)

Только теперь, когда мы выяснили физическую природу «силы тяги», мы можем вернуться к вопросу о том, какую работу она совершает.

А никакой работы она не совершает!

«Что за чепуха? – скажет читатель. – Сила есть, перемещение есть, а работы нету?!».

Именно так! И дело в том, что есть перемещение автомобиля, но нет перемещения той точки тела, в которой приложена сила. Ведь те точки шины, которые в данный момент соприкасаются с дорогой, относительно дороги не перемещаются, и, соответственно, никакой работы сила трения не совершает!

3.

Где мы можем столкнуться с этим фактом, что называется, «лоб в лоб»?

В базовом школьном курсе разговоров о динамике вращательного движения избегают. Но в профильном курсе хоть какое-то представление об этой теме дать необходимо. Полезнейшая задача в этой теме – задача о скатывании (без проскальзывания) цилиндра с наклонной плоскости. И решая её с помощью закона сохранения энергии, учителю придется объяснить ученикам, какова работа сил трения цилиндра о плоскость. (Очень рекомендую коллегам решить эту задачу тремя разными способами).

Знаю, сколь тяжело человеку, впервые столкнувшимся с мыслью о том, что «сила тяги» работы не совершает, примириться с ней. Помню возмущение аудитории на моем докладе на городском учительском семинаре. Помню жаркие споры с коллегами в Физико-Техническом институте.

Но мне нечего добавить к доводам, приведенным выше.

Конечно, об этом можно прочесть в любом хорошем, серьезном учебнике механики, см., например, [2].

Является ли описанное выше свойство силы тяги чем-то специфическим только для колесных «самодвижущихся экипажей»? Конечно, нет. Возьмем «систему» попроще. Какое-нибудь «шагающее самодвижущееся устройство».

Подумаем о том, какая сила приводит в движение человека. Конечно, сила трения наших подошв о дорогу. Наши подошвы относительно дороги, конечно, не проскальзывают. И здесь-то, надеюсь, любому ясно, что эта сила работы не совершает. (Здесь было бы очень интересно отвлечься от основной линии наших рассуждений и подумать о том, на что же мы тратим энергию при ходьбе. По-видимому, на изменение конфигурации тела и на неизбежный подъем центра тяжести. Посмотрите на движение спортсменов, занимающихся ходьбой на длинные дистанции – их странная походка ориентирована как раз на то, чтобы уменьшить расход энергии на подъем центра тяжести).

4.

Но, примирившись с нашей главной мыслью, мы сразу же сталкиваемся со «страшным» вопросом: если сила тяги работы не совершает, то

какая же сила ускоряет автомобиль?!

Почему он «страшный»? Потому что все мы помним «теорему о кинетической энергии»: изменение кинетической энергии К материальной точки равно работе силы, действующей на точку:

(3)

А сила, которую мы считали «силой тяги», как мы выяснили, работы не совершает. Этот вывод с «теоремой о кинетической энергии» согласовать не удастся. Значит, в наших рассуждениях что-то не так – мы в тупике!

Нет, я не прав – ситуация еще хуже! Ведь сила сопротивления воздуха, конечно же, совершает отрицательную работу при движении автомобиля. Мы падаем в бездну!

Снова прошу читателя остановиться и попытаться разрешить противоречие, с которым мы столкнулись, самостоятельно.

5.

Много лет назад я уже писал об этой проблеме, см.[3], но, представляется, что сейчас мне удастся высказаться точнее, чем тогда.

Приглядимся к условию теоремы о кинетической энергии. Для какого объекта она сформулирована? Для материальной точки.

Так вот где зарыта собака!

Приступаем к раскопкам.

Все школьные учебники вводят понятие материальной точки в теме «Кинематика» и в дальнейшем его уже не уточняют. Мне уже приходилось писать [4], что как раз в кинематике-то первое слово в этом составном термине совершенно излишне. Материальность объекта не играет никакой роли в кинематике. Ведь масса, импульс, энергия там остаются за рамками наших рассуждений. А с другой стороны, ничто нам не мешает описывать движение нематериальных объектов (например, тени на земле от летящего самолета).

В динамике же материальность объекта, конечно, принципиальна, но теперь возможность применить эту модель к реальной системе не определяется одним только соотношением размеров.

А что в литературе?

Выбираю самый авторитетный источник из доступных мне на расстоянии вытянутой руки – давний советский пятитомный «Физический энциклопедический словарь». Цитирую: «Практически каждое тело можно рассматривать как материальную точку в случаях, когда расстояния проходимые точками тела, очень велики по сравнению с его размерами» [5, т.3, стр. 154]. Странная какая-то формулировка – слово «практически» размывает смысл утверждения. Но по сути дела ничего нового для нас в ней нет.

Мне кажется, что согласиться с таким утверждением невозможно. Можно или нельзя рассматривать какое-то тело как материальную точку (тем более, в динамике!) зависит от того, на какие конкретно вопросы мы хотим получить ответы.

И здесь-то намечается выход из нашего тупика: если мы пришли к неразрешимому противоречию в рамках модели материальной точки – значит, надо отказаться от этой модели. Надо перейти к более сложной модели автомобиля (человека, собаки…). Вот важнейший вывод из наших рассуждений.

Напомним, какие модели реальных тел рассматриваются в механике (каждая последующая сложнее предыдущей):

- материальная точка,

- твердое тело (система материальных точек, расстояния между которыми не меняются),

- система взаимодействующих материальных точек.

Вот и будем говорить об автомобиле, как о системе взаимодействующих материальных точек.

6.

Итак, пусть автомобиль движется с ускорением. Поставим два четких вопроса, на которые мы должны ответить.

Во-первых, какая сила меняет импульс автомобиля?

И, во-вторых, работа какой силы меняет кинетическую энергию автомобиля?

Ответы на эти вопросы, как мы сейчас увидим, будут коренным образом различаться.

Напомним рассуждения, ведущие к установлению закона изменения полного импульса системы материальных точек (всем они, по-видимому, хорошо известны).

На любую точку системы действуют силы со стороны всех других точек системы (назовем эти силы внутренними) и силы внешние. Пусть – внешняя сила, действующая на i-ю точку, а – сила, с которой k-ая точка системы действует на i-ю.

Для каждой из n точек системы записывается второй закон Ньютона в импульсной форме:

(4)

(штрих над знаком суммы означает, что в сумме по k отсутствует член с k=i). Потом все эти уравнения почленно суммируются. При этом все внутренние силы взаимно уничтожаются вследствие 3-го закона Ньютона. И мы получаем, что изменение полного импульса системы совершают только внешние силы:

(5)

где – сумма внешних сил, действующих на все точки системы (говорить о равнодействующей здесь неуместно):

(6)

Именно этот закон (5) мы имеем в виду, когда говорим о том, что Мюнхгаузен не мог вытащить себя за волосы из болота, или когда ищем именно внешнюю силу, чтобы объяснить ускорение автомобиля (и эту силу мы уже знаем).

7.

Теперь проведем аналогичные рассуждения для работ всех сил, действующих на каждую точку системы.

Для каждой точки системы запишем теорему о кинетической энергии. Над i-ой точкой совершают работу все силы со стороны других точек системы и внешняя сила

(7)

Опять почленно просуммируем все n уравнений. Но теперь никакого взаимного уничтожения членов не произойдет. Поясним это подробнее. Пусть, например, между i-ой и k-ой точками действуют силы отталкивания. Под действием этих сил точки будут удаляться друг от друга. При этом обе силы совершают положительную работу! И при почленном суммировании уравнений работы всех внутренних сил просто сложатся.

Таким образом мы придем к выводу, что изменение полной кинетической энергии системы складывается из работ всех внешних и внутренних(!) сил:

. (8)

Этот вывод разрешает сформулированное выше противоречие. Теперь мы видим что ничего «плохого» в равенстве нулю работы силы тяги нет. При равномерном движении положительная работа внутренних сил компенсирует отрицательную работу сил сопротивления движению. При ускоренном движении часть работы внутренних сил идет на увеличение кинетической энергии автомобиля.

8.

Что можно сказать о силах сопротивления движению?

Заметим, что горизонтальная сила трения ведомых колес о дорогу работы тоже не совершает (по тем же причинам, что указаны выше для силы тяги).

На приведенном выше рисунке мы опустили вертикальные внешние силы, действующие на автомобиль. Это сила тяжести и четыре силы нормальной реакции дороги . ( – равнодействующая всех сил взаимодействия колеса с дорогой в области контакта). Для покоящегося автомобиля силы реакции проходят через оси колес, но при движении автомобиля они смещены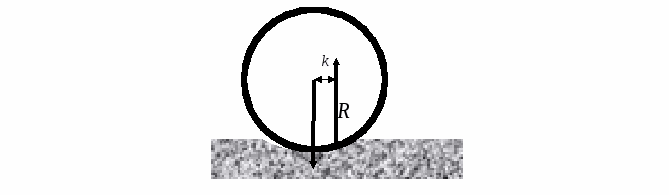

вперед (см.рис.). Моменты этих сил и препятствует вращению колес (т.е. и движению автомобиля в целом). В «Физическом энциклопедическом словаре» и некоторых курсах теоретической механики плечо силы нормальной реакции относительно оси колеса k называют «коэффициентом трения качения» [5, т.5, стр.198; 6, стр.94] (этот коэффициент имеет размерность длины!). В технической литературе поступают иначе. Но обсуждение трения качения не является здесь нашей целью.

Дальнейшее продвижение в анализе движения автомобиля должно быть связано с применением законов динамики вращательного движения и с учетом конкретных технических характеристик двигателя, трансмиссии и т.д.

Литература

1. Кирпичев В.Л. Беседы о механике. М.-Л.: ГИТТЛ, 1950 (4-е изд.). С.155

2. Сивухин Д.В. Общий курс физики. т.1. Механика. М.: Наука, 1989 (3-е изд.). С.271.

3. Рыбаков А.Б. Мы едем, едем, едем…// Физика (ПС), 1996.

4. Рыбаков А.Б. Заметки об изучении кинематики. // Физика (ПС), 2009, №11.

5. Физический энциклопедический словарь. т.1-5. М.: Советская энциклопедия, 1966.

6. Тарг С.М. Краткий курс теоретической механики. М.: Физматлит, 1961.