Описанная окружность.

О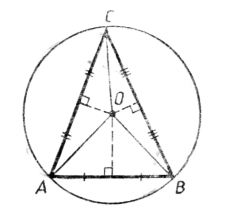пределение: Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в окружность.

Теорема. Около любого треугольника можно описать окружность и притом только одну.

В отличие от треугольника около четырехугольника не всегда можно описать окружность. Например: ромб.

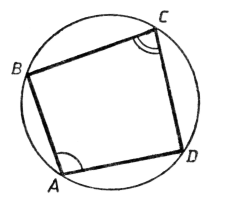
Теорема. В любом вписанном четырехугольнике сумма противоположных углов равна 180⁰.

Если сумма противоположных углов четырехугольника равна 180⁰, то около него можно описать окружность.

Для того чтобы четырехугольник АВСD был вписанным, необходимо и достаточно, выполнения любого из следующих условий:

• ABCD выпуклый четырехугольник и ∟ABD=∟ACD;

• Сумма двух противоположных углов четырехугольника равна 180⁰.

Центр окружности равноудален от каждой из его вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров к сторонам многоугольника, а радиус равен расстоянию от центра до вершин.

Для треугольника: Для правильного многоугольника:

Вписанная окружность.

О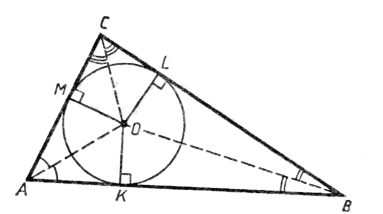пределение: Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

Не во всякий четырехугольник можно вписать окружность. Например: прямоугольник, не являющийся квадратом.

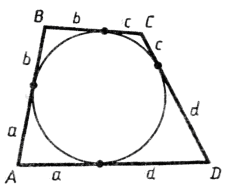
Теорема. В любом описанном четырехугольнике суммы длин противоположных сторон равны.

Если суммы длин противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Для того чтобы выпуклый четырехугольник ABCD являлся описанным, необходимо и достаточно, чтобы выполнялось условие AB+DC=BC+AD (суммы длин противоположных сторон равны).

Центр окружности равноудален от сторон многоугольника, значит, совпадает с точкой пересечения биссектрис углов многоугольника (свойство биссектрисы угла). Радиус равен расстоянию от центра окружности до сторон многоугольника.

Для треугольника: Для правильного

многоугольника: