Урок 4

Тема урока: «Объем и площадь поверхности конических тел»

Тип учебного занятия: изучение и первичное закрепление новых знаний и способов действий в ходе практической работы.

Цели урока:

• Создавать содержательные и организационные условия для восприятия, осмысления и первичного закрепления учащимися понятия «коническое тело». Вывести формулу для вычисления объема конических тел.

• Организовать деятельность учащихся по применению формул площади поверхности и объема конических тел при решении практических задач.

• Содействовать развитию у учащихся умения формулировать проблему, предлагать пути ее решения.

• Воспитывать аккуратность и точность при выполнении практической работы, содействовать у учащихся умения общаться, отстаивать свое мнение и выслушивать мнения товарища.

Оснащение урока:

1. Таблицы «Конические тела», «Объемы конических тел».

2. Учебник по геометрии под редакцией Л.С. Атанасян

3. Модели тел и их развертки

4. Карточки – задания.

Ход урока:

1. Организация занятия.

Проверка готовности учащихся к занятию, постановка целей и задачи урока. Тема урока записывается в тетради и на доске.

II. Повторение ранее изученного материала

1. Проверка домашнего задания

2. Самостоятельная работа по теме «Объем цилиндрического тела»

III. Изучение нового материала

Работа с моделями (параллелепипед, призма, конус, пирамида, цилиндрическая пирамида), (развертки цилиндрических и конических тел)

1. – показать цилиндрические тела

– что общего между всеми цилиндрическими телами?

– как найти площадь поверхности цилиндрических тел?

– какая формула позволяет найти объем цилиндрического тела?

2. – покажите конические тела

- что общего между всеми коническими телами?

- найдите развертку пирамиды и конуса

- как найти площадь поверхности пирамиды?

- как найти площадь поверхности конуса?

Практическая работа:

1) Найдите площадь поверхности пирамиды.

Выполните необходимые измерения и найти площадь поверхности пирамиды.

Sпир = Sосн + Sбок Sбок = Росн h, h – апофема

2) Объем пирамиды.

1. Наглядность: возьмем треугольную призму и пирамиду одинакового основания и высоты. Во сколько раз объем пирамиды будет меньше объема призмы?

Подтверждаем версию, налив воду в модель пирамиды и переливаем ее в модель призмы

значит Vпир = 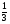Vпризмы Vпир = 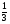Sосн · H

Теорема (стр. 151 п.69 Атанасян)

2. Объем конуса

по выводу формулы объема пирамиды, как объема конического тела даем версию, что Vк = 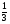Vцил (если Нц=Нк и Sосн.ц. = Sосн.кон.)

теорема (стр.153 п.70)

V = 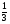Sосн.· H

3) Продолжение практической работы:

Вычислите объем модели конуса, выполнив соответствующие измерения (идет работа в парах)

Vк =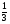Sосн*H

- какую формулу применяем для вычисления площади основания?

Sосн = рR²

R – радиус, измеряем диаметр Д,

Тогда Sосн =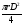

- каким образом можно узнать высоту конуса?

(измеряем L; R и применяем теорему Пифагора)

H =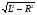

L

H

R

4. Выводы:

- что называют коническим телом?

- какие фигуры можно отнести к коническим телам?

- какие формулы можно применить, чтобы найти Sп.конич.тел, Vкон. тела

IV Домашние задание: № 685, 704 стр.155 Атанасян

V. Итог урока:

• Общая характеристика работы группы;

• Оценки за практическую работу и самостоятельную работу

VI. Рефлексия. Самооценка работы учащихся, выявление пробелов в знаниях и методы их исправления. Вывод учащихся о необходимости изучения данного материала в практической деятельности.

Общая оценка урока учащимися.

Учащиеся ставят «+» в какой-то отдел листа рефлексии

Понял, уроком доволен

Не совсем понял

Ничего не понял

И не хочу понимать!

Приложение к уроку:

Вариант-1

«Объем цилиндрических тел»

По какой формуле можно вычислить объем?

A

B

C

D

1

Поршневого кольца

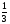πR²H

a∙b∙c

πR²H

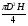
2

Кузова трактора

Т-16М

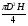
πD²H

a∙b∙c

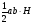
3

Камеру сжатия пускового двигателя

a∙b∙c

a²∙h

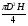
2πR∙H

4

Круговой цилиндр

S_осн.H

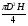
πR²∙H

abc

5

Треугольную призму

πR²H

a∙b∙c

S_осн.H

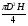
6

Прямоугольный параллелепипед

abc

S_осн.H

a²

πR²H

(проверка заданий по ответам)

Ответы:

1. – C,D

2. – C

3. – C

4. – B,C

5. – C

6. – A,B

По какой формуле можно вычислить

Ответы

Объем конического роликоподшипника

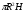
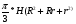
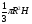
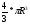
Объем толкателя

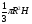
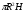
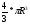
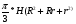
Объем подшипника

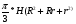
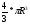
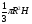
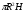
Объем поршневого пальца

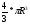
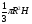
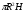
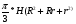
1

2

3

4