Конспект урока по Геометрии "Площадь" 8 класс
Класс: 8.
Тема: «Площадь».
Тип урока: урок повторения и закрепления изученного материала.
Цели:
Общеобразовательные:
1. Систематизировать знаний учащихся.
2. Повторить и еще раз закрепить полученные ранее знания и умения по темам: «Треугольники», «Площадь», «Средняя линия треугольника».
Развивающие:
1. Формирование следующих качеств знаний учащихся: самостоятельность, глубина, осознанность, гибкость и устойчивость мышления.
2. Формирование мыслительных операций (анализ и синтез, сравнение, аналогия, классификация и т.д.).
Воспитательные:
1. Формирование интереса к познанию.
2. Формирование учебных умений по планированию, прогнозированию и моделированию результатов своей деятельности.
3. Выявление широких возможностей более всестороннего воспитания учащихся на уроках математики.
Технология: конструирование мысленных моделей задач; рассмотрение схематических конструкций изучаемых объектов и выполнение над ними ряда мыслительных операций (анализ и синтез, сравнение, аналогия, классификация, абстрагирование, абстракция и т.д.).
Задачи:
1. Ответе на следующие вопросы:
Из каких фигур состоят персонажи на рисунке 16?
Какие виды треугольников вы видите на рисунке 16?
Покажите равнобедренные, равносторонние и разносторонние треугольники.
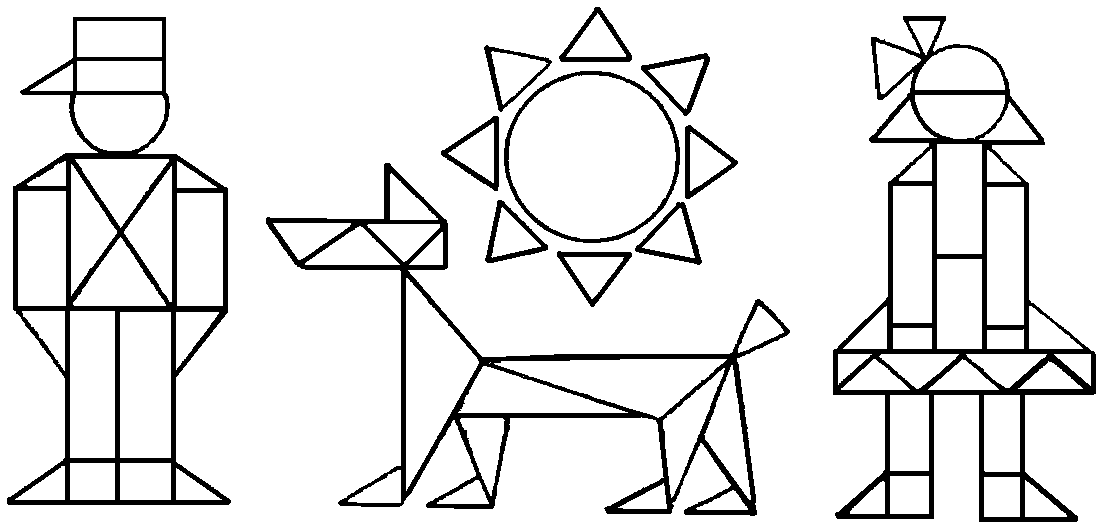
Рис. 16.
(Это задание позволяет определить, на сколько хорошо учащиеся умеют анализировать, сравнивать и наблюдать. Данная задача позволяет формировать у учащихся глубину и устойчивость мышления.)
2. Какую часть площадь заштрихованной фигуры составляет от площади треугольника (рис. 17)?

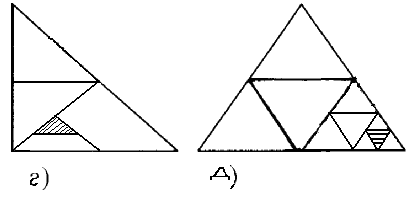
Рис.17.
Решение: Обратим внимание на то, что средняя линия треугольника отсекает от его площади четвертую часть. Тогда если площадь всего треугольника в каждом случае равна S, то площадь заштрихованной фигуры будет равна соответственно  ,
,  ,
, 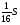 ,
, 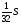 ,
,  .
.
(Это задание позволяет определить на сколько осознано учащиеся владеют такими мыслительными операциями, как анализ и синтез, на сколько хорошо они могут воспользоваться аналогией, сравнением треугольников. Данная задача позволяет формировать у учащихся самостоятельность и глубину мышления.
Следующая задача позволяет проверить на сколько осознано учащиеся решают задания и развивает умение анализировать и обобщать.)
3. В прямоугольнике проведена диагональ (рис.18), в одном из получившихся треугольников проведена медиана. Найдите соотношение между площадями фигур I. II. III.
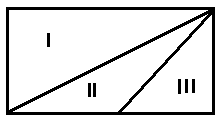
Рис. 18.
Решение: SI:SII:SIII=2:1:1. Пусть площадь прямоугольника равна S, тогда SI=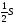 =SII+SIII, SII=SIII=
=SII+SIII, SII=SIII=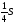 , так как основания и высоты треугольников равны.
, так как основания и высоты треугольников равны.
4 В треугольнике проведена средняя линия. Из середин боковых сторон на основание опущены высоты (рис. 19). Что больше: площадь прямоугольника или сумма площадей заштрихованных треугольников?
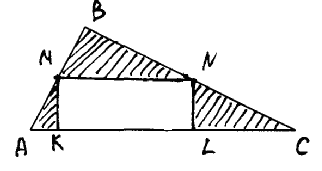
Рис. 19
Решение: Они равны.
Способ первый: Пусть MN – средняя линия треугольника ABC, MK AC, NL
AC, NL AC.
AC.
Проведем отрезок NP||AB (P AC) (рис. 20). Тогда сумма площадей заштрихованных треугольников равна сумме площадей треугольников MBN и PNC.
AC) (рис. 20). Тогда сумма площадей заштрихованных треугольников равна сумме площадей треугольников MBN и PNC.
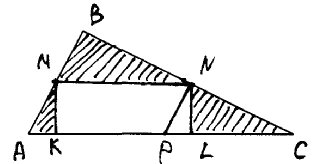
Рис. 20
Площадь каждого из этих треугольников составляет четвертую часть от площади ΔABC. 
 SΔMBN+
SΔMBN+ SΔPNC=
SΔPNC=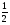 SΔABC
SΔABC
Способ второй: Пусть MN – средняя линия треугольника ABC, MK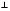 AC, NL
AC, NL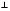 AC.
AC.
Проведем отрезок NP||AB (P AC) (рис.21), также средняя линия треугольника. Проведем третью среднюю линию. Тогда прямоугольник разобьется на три треугольника, каждый из которых равновелик заштрихованному треугольнику
AC) (рис.21), также средняя линия треугольника. Проведем третью среднюю линию. Тогда прямоугольник разобьется на три треугольника, каждый из которых равновелик заштрихованному треугольнику
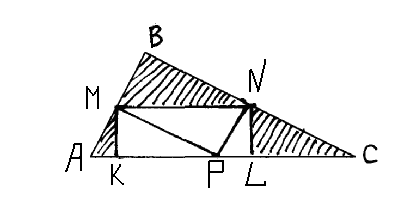
Рис. 21.
(Данная задача имеет несколько способов решения, и отыскание других способов решения способствует развитию глубины и гибкости мышления учащихся.)
5. Площади треугольников, образованных отрезками диагоналей трапеции и ее основаниями, равны S и Q. Найдите площадь трапеции. (Рис.22)
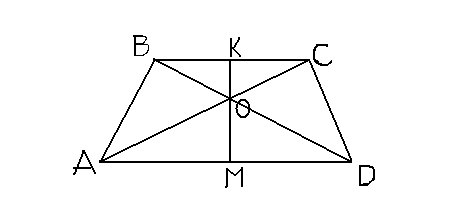
Рис. 22.
Решение:
SΔBOC=S, SΔAOD=Q. KM – высота трапеции. OK высота ΔBOC, OM – ΔAOD.
Обозначим: DC=a, AD=b, OK=ha, OM=hb, тогда KM=ha + hb.
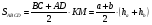
Треугольники ΔBOC и ΔAOD будут подобными (по 3 углам), тогда имеем
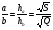 (*)
(*)
Так как 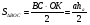 , то
, то 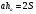 .
.
Так как 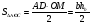 , то
, то 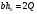 .
.
Из пропорции (*), следует 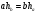 .
.
Получим 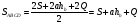
Из (*) получаем 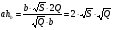 ,
,
Окончательно 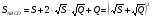 .
.
Ответ: 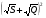 .
.
(Данная задача позволяет понять, на сколько осознано ученик ее решает, т.е. понимает что дано и как это использовать.)
Выводы:
Данный урок позволил определить, на сколько осознано учащиеся умеют анализировать, сравнивать и обобщать при конструирование мыслительных моделей задач. А также сформировать у учащихся самостоятельность и глубину ума при выполнение ряда мыслительных операций.

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ