Конспект урока по Геометрии "СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА" 8 класс
ПЛАН УРОКА:
«ВОСХОЖДЕНИЕ НА МАТЕМАТИЧЕСКИЙ ОЛИМП».
ТЕМА УРОКА:
«СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА».
ГЕОМЕТРИЯ
8 КЛАСС
УЧИТЕЛЬ: Обухова Ольга Викторовна
МБОУ СОШ № 26
г. Мытищи
Московской области
Цель урока: обобщить знания по темам: «площади», «теорема Пифагора», «соотношения между сторонами и углами прямоугольного треугольника», подготовиться к контрольной работе.
Оборудование к уроку: мультимедийный проектор «BENQ», notebook или компьютер, кодоскоп «Лектор – 2000» или сканер, экран или белая доска, учебник «Геометрия 7 – 9» под редакцией Л.С. Атанасяна, раздаточный материал, дипломы для награждения учащихся по итогам работы, «медали».
ПЛАН УРОКА
Организационный момент:
Учащиеся в тетрадях записывают число и тему урока, слушают вступительное слово, которое сопровождается показом слайда.
Сегодня мы проведём урок, который покажет: покорится ли нам математический Олимп, достойны ли мы стать слушателями Академии великого древнегреческого философа. (Презентация «Теоретическая разминка», слайд № 1)
Этот учёный основал в Афинах собственную школу – Академию; ввёл математику в число предметов преподавания, основал логический метод рассуждения от противного; уделял большое внимание геометрическим задачам на построение с помощью циркуля и линейки.
С перечисленными достижениями великого учёного мы уже знакомы. Теперь нам предстоит назвать имя этого учёного.
Теоретический опрос:
Для начала проведём теоретическую разминку (разминка сопровождается показом сменяющихся слайдов, у учащихся на столах лежат готовые формы «Олимпа» для расшифровки криптограммы).
Нам предстоит расшифровать высказывание, которое написал на воротах своей Академии этот учёный, а также узнать его имя. (Презентация «Теоретическая разминка», слайд №2)
Ключ к разгадыванию: (Презентация «Теоретическая разминка», слайды №3 - 18)
12
27
15
21
12
Отношение противолежащего катета к гипотенузе.
11
20
27
28
15
24
18
18
17
12
27
15
21
12
Отношение прилежащего катета к гипотенузе.

«
11
21
12
22
13
«
12
23
14
24
15
25
16
26
17
14
27
22
22
17
22
,
,
18
22
17
15
25
28
15
24
25
22
19
25
17
29
25
22
20
27
23
»
.
11
30
24
22
17
15
.
»
.
.
Отношение противолежащего катета к прилежащему.
22
24
15
19
25
15
12
Многоугольник, площадь которого вычисляется по формуле S = ½ (a ha)
22
20
25
21
19
17
30
13
15
27
18
22
17
9
14
25
12
22
16
17
Выражение sin2α + cos2α = 1
Старинная мера длины, равная примерно 25 мм. Этой единицей измерил рост своей героини Ганс Христиан Андерсен.
14
23
8
29
Древнегреческий учёный, который погрузившись в ванну воскликнул: «Эврика!» и открыл известный в физике закон.
24
20
26
27
29
25
14
ОТВЕТЫ:
12
27
15
21
12
с
и
н
у
с
11
20
27
28
15
24
18
п
р
и
з
н
а
к
18
17
12
27
15
21
12
к
о
с
и
н
у
с
22
24
15
19
25
15
12
т
а
н
г
е
н
с
22
20
25
21
19
17
30
13
15
27
18
т
р
е
у
г
о
л
ь
н
и
к
22
17
9
14
25
12
22
16
17
т
о
ж
д
е
с
т
в
о
24
20
26
27
29
25
14
А
р
х
и
м
е
д
14
23
8
29
д
ю
й
м
(Презентация «Теоретическая разминка», слайд №19)

«
11
21
12
22
13
«
п
у
с
т
ь
12
23
14
24
15
25
с
ю
д
а
н
е
16
26
17
14
27
22
22
17
22
,
в
х
о
д
и
т
т
о
т
,
18
22
17
15
25
28
15
24
25
22
к
т
о
н
е
з
н
а
е
т
19
25
17
29
25
22
20
27
23
»
.
11
30
24
22
17
15
.
г
е
о
м
е
т
р
и
ю
»
.
П
л
а
т
о
н
.
Вступительный экзамен в Академию сдан, но вас ждут и другие испытания.
Проверка домашнего задания:
Ученики Платона решили выяснить: выполняете ли Вы домашнее задание? На дом были заданы задачи № 599 и № 602. Давайте проверим решение задач при помощи кодоскопа (сканера и проектора).
Задачу № 599 было поручено решить ф.и. ученика (ученик объясняет решение задачи, спроектированной на экран).
Спросить после объяснения: были ли другие решения этой задачи, может быть, у кого-нибудь получился другой ответ? При необходимости остановиться на спорных моментах ещё раз.
Задачу № 602 на плёнке было поручено решить ф.и. ученика (ученик только представляет решение задачи, но при наличии времени тоже может объяснить решение).
Выяснить у учащихся: были ли другие решения этой задачи, может быть, у кого-нибудь получился другой ответ? При необходимости остановиться на спорных моментах ещё раз.
Вы доказали, что являетесь прилежными учениками и выполняете домашнее задание самостоятельно, а не «сдуваете» его из ГДЗ. Но вас ждёт очередная проверка. Последователи Платона подготовили блиц – опрос.
Блиц – опрос:
(Работа по готовым чертежам). На оборотной стороне доски начерчены чертежи, на которые нанесены имеющиеся данные для решения каждой задачи. У учащихся на столах тоже лежат листы с готовыми чертежами.
№ 1
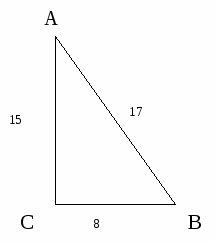
Дан прямоугольный треугольник АВС. Из вариантов ответов на следующие вопросы выберите правильные.
1. Чему равен cos A?
Ответ: а) cos A = 8/15; б) cos A = 8/17;
в) cos A = 17/15; г) cos A = 15/17.
2. Чему равен sin B?
Ответ: а) sin B = 8/15; б) sin B = 8/17;
в) sin B = 17/15; г) sin B = 15/17.
А
s
 in B = 17/15Чему Равен tg B?
in B = 17/15Чему Равен tg B?
О твет: а) tg B = 8/15; б) tg B = 8/17; в) tg B = 17/15; г) tg B = 15/17.
твет: а) tg B = 8/15; б) tg B = 8/17; в) tg B = 17/15; г) tg B = 15/17.
Правильные ответы:
г) cos A = 15/17
г) sin B = 15/17
Правильного ответа нет; tg B = 15/8.
№ 2.
2.
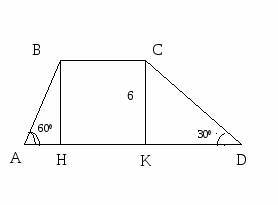
Углы при основании трапеции равны 60° и 30°, высота трапеции равна 6 см. Найдите боковые стороны трапеции.
Решение: в Δ АВС ![]()
![]() ,
, ![]() ,
,
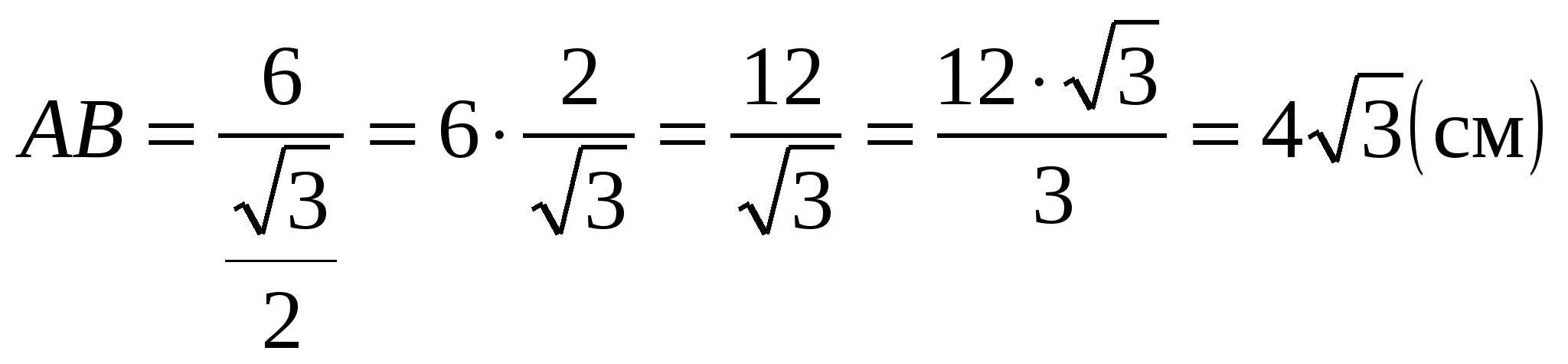
в Δ CKD ![]() , катет СК лежит против
, катет СК лежит против ![]() , следовательно
, следовательно ![]()
№ 3.
3.
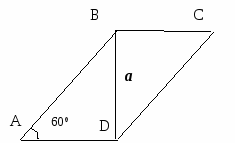
Диагональ параллелограмма равна а и перпендикулярна его стороне. Найдите стороны параллелограмма, если один из углов параллелограмма равен 60°.
Решение: в Δ ABD ![]() ,
, ![]()
![]() , следовательно
, следовательно ![]() .
.
![]() , следовательно
, следовательно 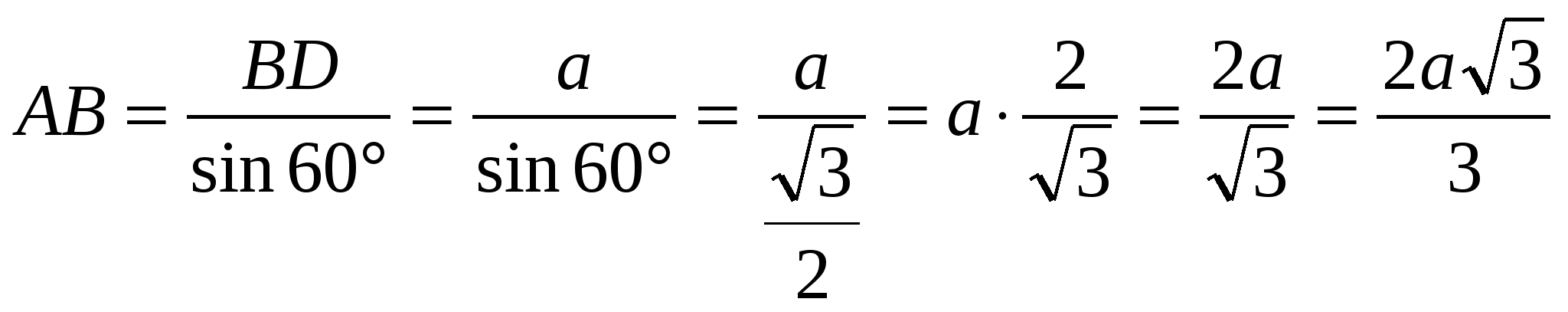
Вы успешно прошли и это испытание. Мы поднялись ещё на одну ступеньку математического Олимпа. За решение этих задач Боги – математики послали вам «медали». Вручить медали тем, кто наиболее активно участвовал в решении задач блиц – опроса.
Решение задачи в тетрадях:
Но ученики Платона считают, что недостаточно проверили Ваши знания по геометрии и вызывают Вас на очередной поединок. Они приготовили задачу № 601 из учебника и дополнили её вопросами. Кто же сразится за звание лучшего геометра школы № 26?
(чертёж к задаче мною заготовлен на доске заранее, данные задачи из учебника записаны, а дополнительные вопросы в данные задачи дописывает отвечающий.)
Задача № 601.
Д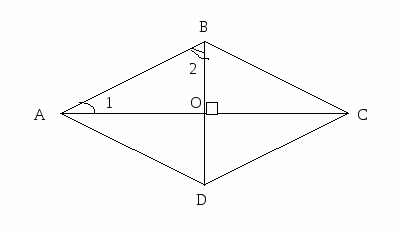 ано: ABCD – ромб,
ано: ABCD – ромб, ![]() ,
, ![]() .
.
Найти: ![]()
Решение: ![]()
В Δ АОВ ![]()
![]()
![]() , следовательно
, следовательно ![]() .
.
![]() .
.
Так как АС и BD биссектрисы углов ромба, то
![]()
![]() ,
, ![]() .
.
Так как диагонали ромба взаимно-перпендикулярны, то
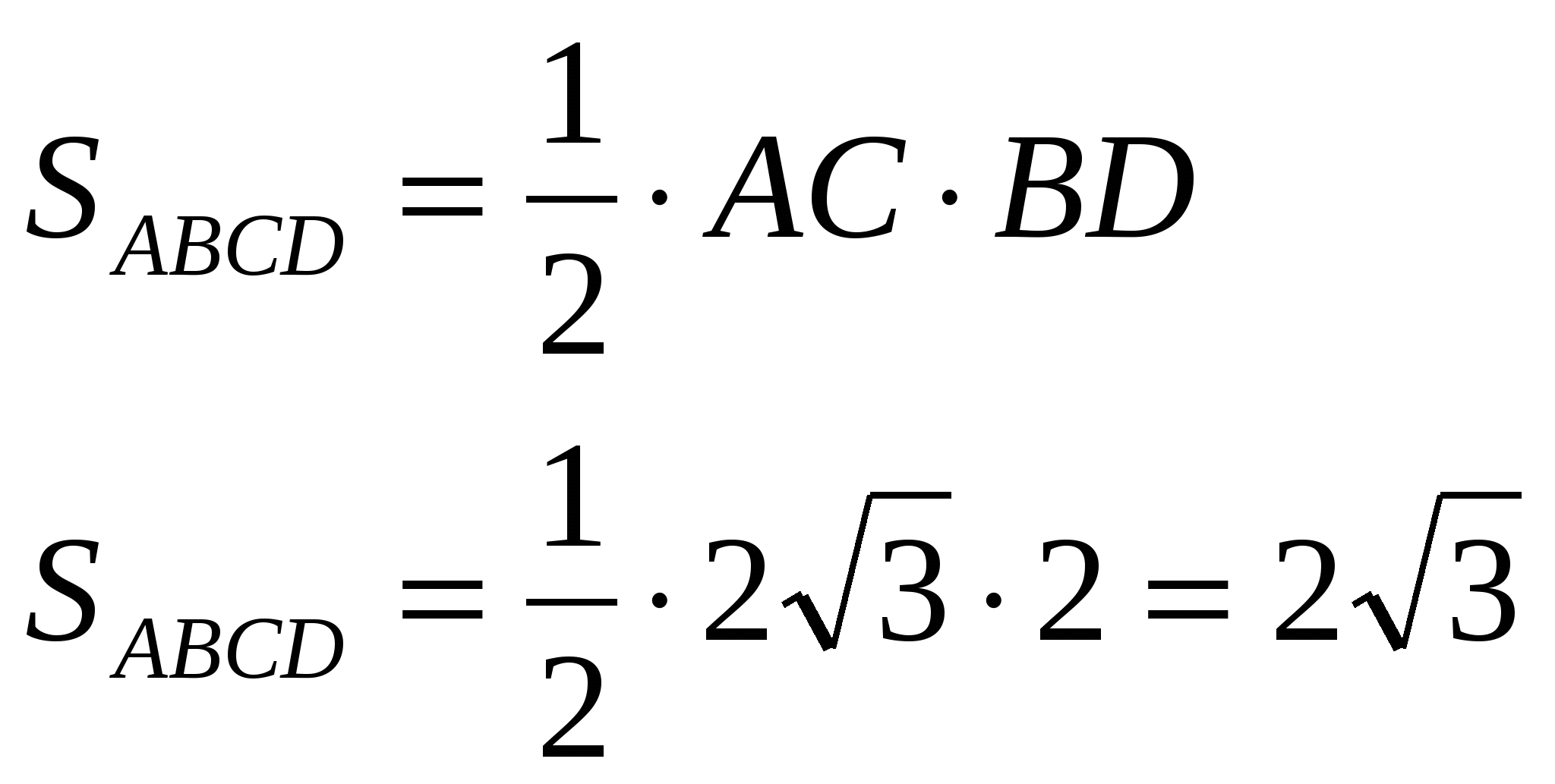
Из Δ АОВ по теореме Пифагора находим АВ:
![]()
или ![]() , тогда
, тогда 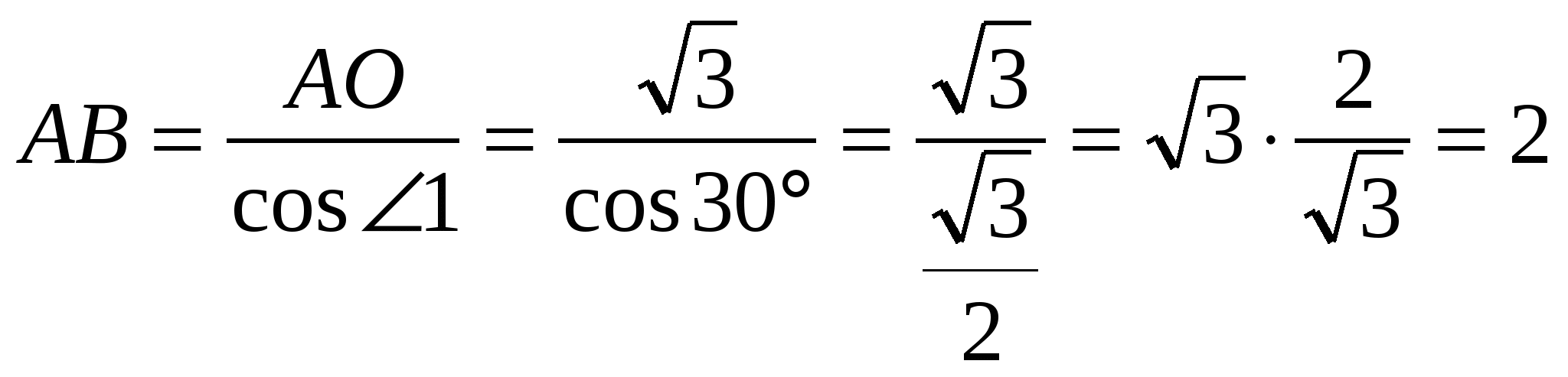
Ответ: 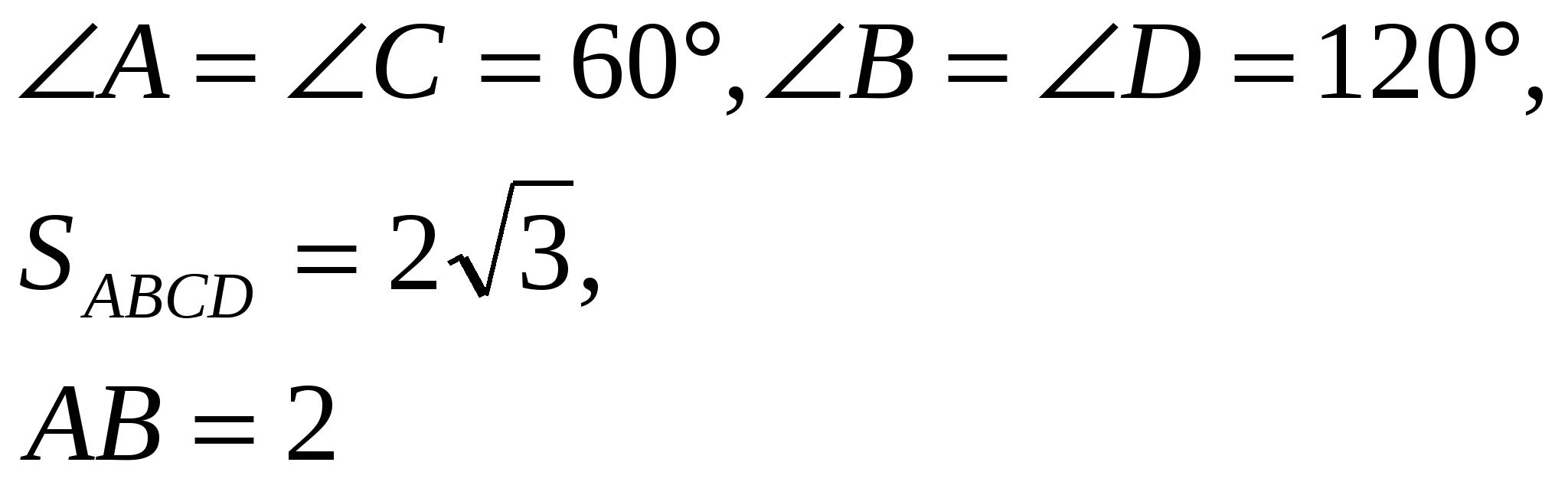
По окончании решения задачи вручить «медаль» лучшему геометру школы № 26. Если будут помощники при решении этой задачи, то вручить медали и им, объяснив, что команда 8 класса сплочённая, и товарищей своих они всегда поддерживают.
Осталось подняться на самую верхнюю ступеньку Олимпа. Вам предстоит пройти заключительное испытание.
Кросснамбер:
Лучшие ученики Платона подготовили для вас кросснамбер «Прямоугольный треугольник». (Презентация «Кросснамбер. Прямоугольный треугольник», слайд № 1).
(Кросснамбер – один из видов числовых ребусов. В переводе с английского языка слово «кросснамбер» означает «кресточислица». В каждую клетку кресточислицы вписывается по одной цифре от 0 до 9. А для того, чтобы не было путаницы, номера заданий обозначают буквами.) (Презентация «Кросснамбер. Прямоугольный треугольник», слайд № 2).
Учащиеся получают листы с текстом кросснамбера, в которых решают предложенные задачи. (Презентация «Кросснамбер. Прямоугольный треугольник», слайд № 3). Затем в таблицу вписывают ответы к задачам и заполняют поле кросснамбера.
1 ВАРИАНТ
По горизонтали:
б) Чему равен квадрат катета прямоугольного треугольника с гипотенузой, равной 13 см и другим катетом, равным 5 см.
г) В прямоугольном треугольнике катет равен 4 см, а косинус прилежащего угла равен 0,4. Чему равна гипотенуза?
д) Тангенс какого угла равен 1?
е) Чему равна площадь треугольника с катетами, равными 38 см и 9 см?
По вертикали:
а) В прямоугольном треугольнике гипотенуза равна 20 см, а синус одного из острых углов равен 0,7. Чему равен катет, противолежащий данному острому углу?
б) наименьшее простое трёхзначное число.
в) число (б) по горизонтали, записанное от конца к началу.
ж) Чему равна половина площади квадрата со стороной, равной 12 см?
2 ВАРИАНТ
По горизонтали:
б) Чему равен квадрат катета прямоугольного треугольника с гипотенузой, равной 15 см и другим катетом, равным 9 см.
г) В прямоугольном треугольнике катет равен 8 см, а косинус прилежащего угла равен 0,8. Чему равна гипотенуза?
д) Синус и косинус какого угла равны?
е) Чему равна площадь треугольника с катетами, равными 19 см и 18 см?
По вертикали:
а) В прямоугольном треугольнике гипотенуза равна 40 см, а синус одного из острых углов равен 0,35. Чему равен катет, противолежащий данному острому углу?
б) наименьшее простое трёхзначное число.
в) число (б) по горизонтали, записанное от конца к началу.
ж) 122:2
а
б
в
г
д
е
ж
Работа над кросснамбером и последующая его проверка осуществляются показом слайдов. (Презентация «Кросснамбер. Прямоугольный треугольник», слайды № 4 и 5).
Проверка кросснамбера осуществляется учащимися. Соседи по парте меняются листами и проверяют задания друг у друга. Затем по предложенным критериям оценивания работы выставляют оценку за разгаданный кросснамбер, подписывая фамилию проверяющего.
По горизонтали:
б) 144
г) 10
д) 45
е) 171
По вертикали:
б) 14
г) 101
д) 441
е) 72
а
1
б
1
4
в
4
г
1
0
д
4
5
е
1
ж
7
1
2
Ну вот и завершилось последнее испытание. Лучшие ученики Платона по достоинству оценили учащихся 8 класса школы № 26 и вручают Вам Дипломы.
Каждый проверяющий выписывает за выполненную работу «Диплом слушателя Академии Платона». Каждому диплому присвоена I, II, или III степени.
Оценка «5»
Диплом I степени
Оценка «4»
Диплом II степени
Оценка «3»
Диплом III степени
ДИПЛОМ
____ СТЕПЕНИ
ВРУЧАЕТСЯ ________________________
СЛУШАТЕЛЮ АКАДЕМИИ ПЛАТОНА.
ЭТОТ ДИПЛОМ ДАЁТ ПРАВО НА ДАЛЬНЕЙШЕЕ ИЗУЧЕНИЕ МАТЕМАТИЧЕСКОЙ НАУКИ.
УЧЕНИКИ ПЛАТОНА:
ОБУХОВА О.В.
В диплом можно вписать фамилии коллег, присутствовавших на уроке.
Домашнее задание:
§ 4, п.п.66 – 67, вопросы 15 – 18 к главе VII, задача № 603.
Подготовиться к контрольной работе.
Задачи домашнего задания:
Задача № 599.
Д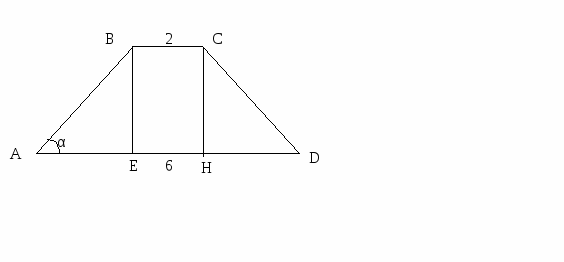 ано: ABCD – трапеция, AB=CD,
ано: ABCD – трапеция, AB=CD,
BC=2 см, AD=6 см, ![]() .
.
Найти: ![]()
![]() .
.
Решение: ![]() .
.
В Δ ΑΒΕ ![]() . В Δ CDH
. В Δ CDH ![]() . Δ ΑΒΕ=Δ CDH по гипотенузе и острому углу:
. Δ ΑΒΕ=Δ CDH по гипотенузе и острому углу:
АВ=CD, ![]() (так как трапеция ABCD – равнобедренная).
(так как трапеция ABCD – равнобедренная).
Значит ![]() . Четырёхугольник
. Четырёхугольник ![]() - прямоугольник, так как
- прямоугольник, так как ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() . Тогда
. Тогда ![]() и
и ![]() .
. ![]() , тогда
, тогда ![]() .
.
![]() .
.
Ответ: ![]()
Задача № 602.
Дано: ABCD 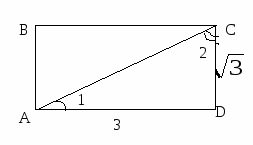 прямоугольник.
прямоугольник.
![]() .
.
Найти: ![]() и
и ![]() .
.
Решение: так как ABCD прямоугольник, то ![]() . Следовательно, Δ АCD – прямоугольный.
. Следовательно, Δ АCD – прямоугольный.
Пусть ![]() а
а ![]() . Тогда
. Тогда ![]() , то есть
, то есть ![]() . Но
. Но ![]() , тогда
, тогда ![]() .
.
Ответ: ![]() .
.

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ