Рабочая прграмма по геометрии 7 класс
Рабочая программа по алгебре
8 класс
Учебник для 8 класса общеобразовательных учреждений. / Под ред. Ш.А. Алимова, Ю.М. Колягина, Ю.В. Сидорова и др. //Москва «Просвещение», 2011
Программа составлена на основе программы для общеобразовательных учреждений 7-9 класс, составитель Бурмистрова;
Автор: Сторожко Татьяна Васильевна,
учитель математики МОУ «Неверовская СОШ»
1. Пояснительная записка.
Программа составлена на основе программы для общеобразовательных учреждений 7-9 класс, составитель Бурмистрова;использованием учебника «Алгебра». Учебник для 8 класса общеобразовательных учреждений. / Под ред. Ш.А. Алимова, Ю.М. Колягина, Ю.В. Сидорова и др. //Москва «Просвещение», 2011
Целью изучения курса алгебры 8класса является развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов, усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников.
Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теории обобщений и дедуктивных заключений.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
Интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
Воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека
2. Описание курса.
Общеучебные цели:
- создание условий для формирования умения логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки;
- создание условий для формирования умения ясно, точно и грамотно выражать свои мысли в устной и письменной речи;
- формирование умения использовать различные языки математики: словесный, символический, графический;
- формирование умения свободно переходить с языка на язык для иллюстрации, интерпретации, аргументации и доказательства;
- создание условий для плодотворного участия в работе в группе; формирования умения самостоятельно и мотивированно организовывать свою деятельность;
- формирование умения применять приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств тел при решении практических задач, используя при необходимости справочники и вычислительные устройства;
- создание условий для интегрирования в личный опыт новой, в том числе самостоятельно полученной, информации.
Общепредметные цели:
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни: для изучения школьных естественнонаучных дисциплин на базовом уровне; получения образования в областях, не требующих углубленной математической подготовки;
- развитие логического мышления, алгоритмической культуры, пространственного воображения; критичности мышления на уровне, необходимом для обучения в высшей школе, в будущей профессиональной деятельности;
- воспитание средствами математической культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для общественного прогресса.
3. Место курса в учебной плане.
Рабочая программа полностью соответствует требованиям федерального компонента государственного стандарта общего образования и ГОС (национально-региональному компоненту).
Согласно Федеральному базисному учебному плану рабочая программа рассчитана на реализацию в течение 34 учебных недель в объеме 102 часов, в неделю – 3 часа.
4. Личностные результаты.
Личностными результатами обучающихся являются: готовность ученика целенаправленно использовать знания в учении и в повседневной жизни для исследования математической сущности предмета (явления, события, факта); способность характеризовать собственные знания по предмету, формулировать вопросы, устанавливать, какие из предложенных математических задач могут быть им успешно решены; познавательный интерес к математической науке.
Метапредметными результатами обучающихся являются: способность анализировать учебную ситуацию с точки зрения математических характеристик, устанавливать количественные и пространственные отношения объектов окружающего мира, строить алгоритм поиска, анализа и классификации необходимой информации, определять логику решения практической и учебной задачи; умение моделировать — решать учебные задачи с помощью знаков (символов), планировать, контролировать и корректировать ход решения учебной задачи. Использование разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Предметными результатами являются овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
Создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
5. Планируемые результаты.
Должны знать/понимать:
- значение математической науки для решения задач, возникающих в теории и практике;
- значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки; историю развития понятия числа;
- универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности.
Должны уметь:
- выполнять арифметические действия, сочетая устные и письменные приемы; находить значение корня натуральной степени, используя при необходимости вычислительные устройства, пользоваться оценкой и прикидкой при практических расчетах;
- составлять буквенные выражения и формулы по условию задачи; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одно выражение через другие;
- выполнять основные действия со степенями, с многочленами и алгебраическими дробями; выполнять разложение многочлена на множители, выполнять тождественные преобразования рациональных выражений;
- применять свойства арифметического квадратного корня для вычисления значений и преобразования выражений, содержащих квадратные корни;
- решать линейные, квадратные и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений;
- решать линейные и квадратные неравенства с одной переменной и их системы;
- решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
- изображать числа точками на координатной прямой;
- определять координаты точки плоскости, строить точки с заданными координатами, изображать множество решений линейного неравенства;
- находить значения функции, заданной формулой, таблицей, графиком, по ее аргументу, находить значение аргумента по значению функции, заданной графиком или таблицей;
- определять свойства функции по ее графику, применять графическое представление при решении уравнений, систем, неравенств;
- описывать свойства изученных функций, строить их графики.
Владеть компетенциями: познавательной, коммуникативной, информационной, рефлексивной.
Решать следующие жизненно – практические задачи:
- самостоятельно приобретать и применять знания в различных ситуациях.
- аргументировать и отстаивать свою точку зрения;
- уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов;
- пользовать предметным указателем энциклопедий и справочников для нахождения информации;
- самостоятельно действовать в ситуациях неопределенности при решении актуальных для них проблем.
7. Материально- техническое обеспечение.
Учебники
«Алгебра». Учебник для 8 класса общеобразовательных учреждений. / Под ред. Ш.А. Алимова, Ю.М. Колягина, Ю.В. Сидорова и др. //Москва «Просвещение», 2011
Учебные пособия для учителя
«Поурочные разработки по алгебре» к учебнику Ю.Н. Макарычева, Ш.А. Алимова 7 класс, составители А.Н. Рурукин, Москва, «Вако», 2010.
«Поурочные планы» алгебра 7 по учебникам Ш.А. Алимова, составитель Е.Г. Лебедева, Волгоград, «Учитель», 2003
Примерные программы основного общего образования, математике, 2-е издание, Москва, «Просвещение», 2009
Инструментарий мониторинга результатов
«Алгебра, КИМ», 8 класс, Л.Ю. Бабошкина, Москва, «Вако», 2011
«Карточки-задания», алгебра 8 класс, А.А.Таланова, Н.С.Антонова, Москва, «Владос»
«Математика 8 класс», самостоятельные и контрольные работы, А.П.Ершова, В.В. Голобородько, Москва, «Илекса», 2001
9. Основные виды контроля.
Текущий (математический диктант, тест, самостоятельная работа)
Промежуточный (тест, самостоятельная работа, практическая работа);
Итоговый (контрольная работа).
Критерии оценивания работы:
6-7 заданий базового уровня – «3»,
8-10 заданий – «4»,
11-12 заданий – «5».
Предложенные рекомендации условны, так как не стоит забывать о психологической особенности каждого ученика.
Тест за первую четверть (8 кл)
Вариант 1
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Сколько целых чисел удовлетворяют неравенству -8 < x < 4?
1) 12 2) 10 3) 9 4) 11
A2. Решите уравнение:(х + 3) · (х + 4) = 0
1) – 3 и – 4 2) 3 и 4 3) – 3 и 4 4) другой ответ
A3. Выберите верное утверждение.
1) Если а > 5, в > 7, то а + в > 10;
2) если а < 7, в < 3, то а в < 21;
3) если а > 4, в > 6, то а в > 25;
4) если -12 < а < 10, то -10 < 2 а < 12;
А 4. Куплены 8 тетрадей и 4 блокнота. Цена тетради не превосходит 5руб., а блокнота — не превосходит 10 руб. Оцените стоимость S (руб.) покупки.
1) S < 80; 2) S > 80; 3) S ![]() 80; 4) S
80; 4) S ![]() 80.
80.
А5. Какие из чисел -0,5, -1, 1 и 0,5 являются решением неравенства -3х – 4 > х – 1?
1) 0,5; 1 2) -1; 3) 1 4) -0,5; 1; 0,5.
А 6. Округлите до сотых 0,64859.
1) 0,65; 2) 0,6; 3) 0,64; 4) 0,649.
А 7. Решите систему неравенств ![]()
1) x<-13; 2) -13x<-2; 3) -14
Часть В.
К каждому заданию этой части записать краткий ответ.
B1. Найдите наименьшее целое число n, удовлетворяющее двойному неравенству — 4 < n < 4.
B2. Запишите в стандартном виде число 0,000254.
B3. При каких значениях х функция у = 0,5х – 3 принимает положительные значения?
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С1. Решите уравнение |![]() | =
| = ![]() .
.
С2. Решите неравенство |2х - 7| < 3.
Тест за первую четверть (8 кл)
Вариант 2
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Сколько целых чисел удовлетворяют неравенству -11 < x < 2?
1) 11 2) 12 3) 10 4) 9
A2. Решите уравнение: (х + 2) · (- х + 5) = 0
1) – 2 и – 5 2) 2 и - 5 3) – 2 и 5 4) другой ответ
A3. Выберите верное утверждение.
1) Если а > 4, в > 6, то а + в > 9;
2) если а < 4, в < 5, то а в < 20;
3) если а > 5, в > 7, то а в< 36;
4) если -10 < а< 12, то -8 < 2 а < 14.
А 4. Стороны треугольника не превосходят соответственно 0,7м; 1,2м; 1,8м. Оцените периметр
Р (м) данного треугольника.
1) Р< 3,7 2) Р >3,7 3) Р ![]() 3,7 4)
3,7 4)![]() Р
Р ![]() 3,7
3,7
А5. Какие из чисел -2,5, -1, 1 и 2,5 являются решением неравенства -2х + 3 < 3х - 4 ?
1) -1; 1 2) 1; 2,5 3) 2,5 г4 -2,5.
А 6. Округлите до сотых 0,53748.
1) 0,5; 2) 0,54; 3) 0,53; 4) 0,537.
А7. Решите систему неравенств 
1) x>-2; 2) -2<x3; 3) x≥ -3; 4) не имеет решения.
Часть В.
К каждому заданию этой части записать краткий ответ.
B1. Найдите наибольшее целое число n, удовлетворяющее двойному неравенству - 4 < n < 4.
B2. Запишите в стандартном виде число 254345.
B3. При каких значениях х функция у = 0,5х – 4 принимает отрицательные значения?
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1. Решите уравнение |![]() | =
| = ![]() .
.
С 2. Решите неравенство |1 + 5х | < 4.
Тест за вторую четверть (8 кл)
Вариант 1
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Вычислите ![]() .
.
1) 7; 2) ![]() ; 3) 5; 4)
; 3) 5; 4) ![]() .
.
А 2. Вычислите ![]() .
.
1) 7; 2) ![]() ; 3)
; 3) ![]() ; 4) 4.
; 4) 4.
A3. Внесите множитель под знак корня ![]() .
.
1) ![]()
![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; 4)
; 4)![]() .
.
А 4.Вынесите множитель из-под знака корня 0,2 ![]() .
.
1) 0,1![]() ; 2)
; 2) ![]() ; 3) 0,5
; 3) 0,5![]() ; 4)
; 4)![]() .
.
А5. Исключить иррациональность из знаменателя ![]() .
.
1) ![]() ; 2)
; 2) ![]() ; 3) 4 (
; 3) 4 (![]() ); 4) 4.
); 4) 4.
А 6. Найдите значение выражения ![]() при х = 5.
при х = 5.
1) 4; 2) 16; 3)![]() ; 4) 10.
; 4) 10.
А 7. Упростите выражение ![]() , а>0, в> 0.
, а>0, в> 0.
1)![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
Часть В.
К каждому заданию этой части записать краткий ответ.
B1. Какое число меньше ![]() или
или ![]() ?
?
B2. Упростите выражение:![]() при
при ![]() .
.
B3. Выполнить действия: ![]() .
.
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1. Сократите дробь: ![]() .
.
С 2. Извлечь квадратный корень из выражения: ![]() .
.
Тест за вторую четверть(8 кл)
Вариант 2
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Вычислите ![]() .
.
1) 2; 2)6; 3) 4; 4)![]() .
.
А 2. Вычислите ![]() .
.
1) 2; 2)6; 3) 4; 4)![]() .
.
A3. Внесите множитель под знак корня ![]() .
.
1) ![]()
![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; 4)
; 4)![]() .
.
А4.Вынесите множитель из-под знака корня ![]()
![]() .
.
1) 3![]() ; 2) 9
; 2) 9![]() ; 3) 3
; 3) 3![]() ; 4)
; 4)![]() .
.
А 5. Исключить иррациональность из знаменателя ![]() .
.
1) ![]() ; 2)
; 2) ![]() ; 3) 3 (
; 3) 3 (![]() ); 4) 3.
); 4) 3.
А 6. Найдите значение выражения ![]() при х = - 5.
при х = - 5.
1) 4; 2) 6; 3) ![]() ; 4) 36.
; 4) 36.
А 7. Упростите выражение ![]() , а>0, в> 0.
, а>0, в> 0.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
Часть В.
К каждому заданию этой части записать краткий ответ.
B1. Какое число больше 7![]() или
или ![]() ?
?
B2. Упростите выражение:![]() при
при ![]() .
.
B3. Выполнить действия: ![]() .
.
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1. Сократите дробь: ![]() .
.
С 2. Извлечь квадратный корень из выражения: ![]() .
.
Тест за третью четверть(8 кл)
Вариант 1
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Дискриминант уравнения 5х2 -3х+2 = 0 равен
1)19; 2)-1; 3) 49; 4)-31.
А 2. При каком условии полное квадратное уравнение не имеет корней.
1) D=0 2) D>0 3) D<0
A3. Среди чисел 2; 3; -3; -4 найдите корень уравнения х![]() - х-12=0.
- х-12=0.
1) -3; 2) 3; 3) 2; 4) -4.
А 4.Сумма корней уравнения ![]() равна
равна
1) 3; 2) -3; 3) 7; 4) -7.
А5. Произведение корней уравнения ![]() равно
равно
1) 5; 2) -5; 3) 25; 4) -25.
А 6. Решите уравнение 0,5у2 = 8
1) 2;-2; 2) 2; 3) 4;-4; 4) 4;
А 7. Найдите b в уравнении x2+bx-12=0,если оно имеет корень 4.
1) 1; 2) -1; 3) 7; 4) -7.
Часть В
К каждому заданию этой части записать краткий ответ.
B1. Найдите разность большого и меньшего корней уравнения х2+5х-24=0.
B2. Одно число меньше другого на 4, а их произведение равно 221. Найдите эти числа.
B3. Разложите на множители х2 – 10х+9.
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1.Решите систему уравнений 
С 2. Сократите дробь ![]() .
.
Тест за третью четверть(8 кл)
Вариант 2
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Дискриминант уравнения 7х2 +6х+1 = 0 равен
1)32; 2)2; 3) -64; 4) 8.
А 2. При каком условии полное квадратное уравнение имеет единственный корень.
1) D=0; 2) D>0; 3)D<0.
A3. Среди чисел -3; 3; -4; 1 найдите корень уравнения х![]() +5х+6=0.
+5х+6=0.
1) 3; 2) -3; 3) -4; 4) 1.
А 4. Сумма корней уравнения ![]() равна
равна
1) 3; 2) -3; 3) 8; 4) -8.
А 5. Произведение корней уравнения ![]() равно
равно
1) 3; 2) -3; 3) 9; 4) -9.
А 6. Решите уравнение ![]() а2=100
а2=100
1) 5; 2) 20; 3) 5;-5 4) 20; -20
А 7. Найдите с в уравнении 2x![]() +8x+c=0, если оно имеет корень 5.
+8x+c=0, если оно имеет корень 5.
1) 90; 2) -90; 3) 45; 4) -45.
Часть В.
К каждому заданию этой части записать краткий ответ.
B1. Найдите разность большего и меньшего корней уравнения х2-9х+14=0.
B2. Длина прямоугольника больше его ширины на 6 см. Найдите стороны прямоугольника, если площадь равна 112см2.
B3. Разложите на множители х2 +10х+9.
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1. Решите систему уравнений 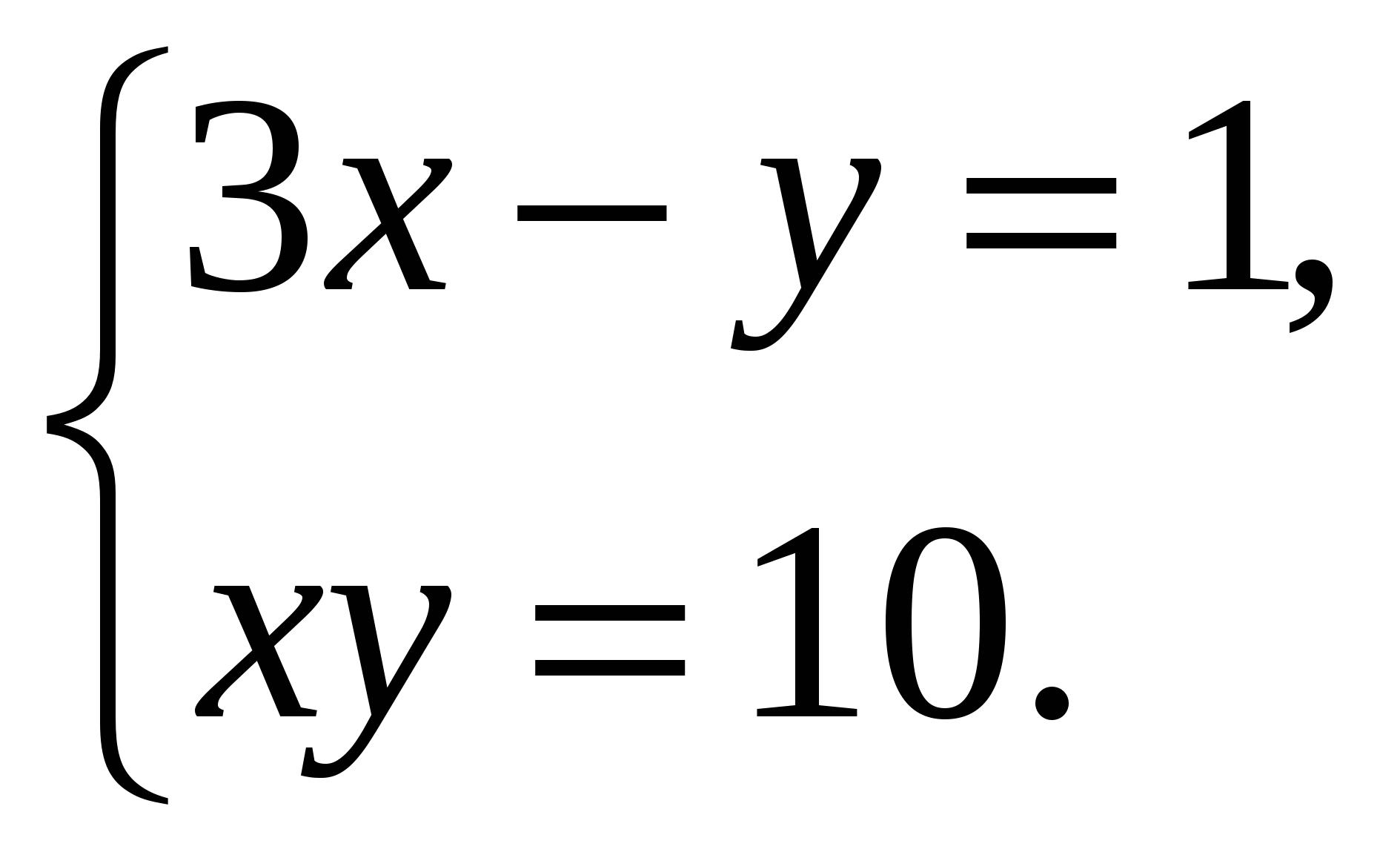
С 2. Сократите дробь ![]() .
.
Итоговый тест (8 кл)
Вариант 1
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
А1. Какая из функций является квадратичной?
1) у = х+2х2 – 3; 2) у = х2 – х3; 3) у = 5х – 1; 4) у = ![]() - х2.
- х2.
A2. Найдите нули функции у = 3х2 – 5х + 2.
1) -1 и 0; 2) 1 и ![]() ; 3) -1 и
; 3) -1 и ![]() ; 4)3 и 2.
; 4)3 и 2.
А 3. Координаты вершины параболы, заданной уравнением у = - х2 +6х, равны
1) (6;0) 2) (-3;-9) 3) (3;9) 4) (0;0)
A4. Найдите наименьшее значение функции у = х2 – 4х + 5.
1) 1; 2)-1; 3) 5; 4) – 4.
![]()
А5. Какое неравенство не является квадратным?
1) х2 + х![]() 0; 2) 3х2 – 5х + 2 < 0; 3) х2 – х3
0; 2) 3х2 – 5х + 2 < 0; 3) х2 – х3 ![]() 0; 4) х2 – 13х + 40 > 0.
0; 4) х2 – 13х + 40 > 0.
А 6. Какое из чисел не является решением неравенства 3х2 – х - 2 < 0?
1) 0,2; 2) 0; 3)-0,5; 4) -1.
А 7. Найдите решения неравенства 3х –х2 <0
1) х >3 2) х<0; х>3 3) х<0 4) 0<х<3
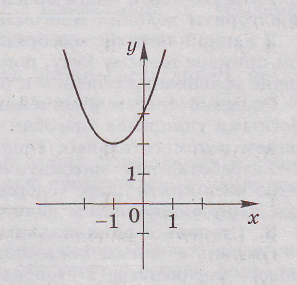
К каждому заданию этой части записать краткий ответ.
В1. На каком промежутке функция, график которой
изображён на рисунке, убывает?
B2. Принадлежит ли графику функции у = х2 – 13х + 40
точка А (4;4)?
B3. При каких значениях х значения функции
у = х2 - 4 отрицательны?
Часть С.
Решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1. Построить график функции у = х2 – 4х + 3.
С 2. Решить неравенство х2 – 4х + 3![]() 0.
0.
Итоговый тест (8 кл)
Вариант 2
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
А1. Какая из функций не является квадратичной?
1) у = х + 2х2; 2) у = х2 – х - 5; 3) у = х2 – 1; 4) у = ![]() - х2.
- х2.
A2. Найдите нули функции у = -3х2 – 5х - 2.
1) -1 и - ![]() ; 2) 1 и
; 2) 1 и ![]() ; 3) 1 и 0; 4) -3 и -2.
; 3) 1 и 0; 4) -3 и -2.
А 3. Координаты вершины параболы, заданной уравнением у = - х2 - 4х +1, равны
1) (-2;5) 2) (2;-3) 3) (4;1) 4) (0;1)
A4. Найдите наибольшее значение функции у = -х2 + 4х - 5.
1) 1; 2)-5; 3) -1; 4) 4.
А 5. Какое неравенство является квадратным?
1) х2 + ![]()
![]() 0; 2) 3х2 – 5
0; 2) 3х2 – 5![]() + 2 < 0; 3) х2 – х3
+ 2 < 0; 3) х2 – х3 ![]() 0; 4) х2 – 13х + 40 > 0.
0; 4) х2 – 13х + 40 > 0.
А 6. Какое из чисел является решением неравенства -3х2 – х + 2 > 0?
1) 2; 2) 0; 3)25; 4) -1.
А 7. Найдите решения неравенства ![]()
1) 0<х<4 2) -4<х<0 3) х>0 4) х<-4;х>0.
Часть В.
К каждому заданию этой части записать краткий ответ.
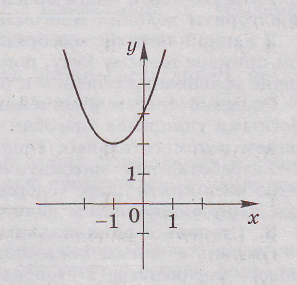
В1. На каком промежутке функция, график которой
изображён на рисунке, возрастает?
B2. Принадлежит ли графику функции
у = х2 – 11х + 24 точка А (2;6)?
B3. При каких значениях х значения функции
у = -х2 + 4 положительны?
Часть С.
Решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1. Построить график функции у = х2 – 6х + 5.
С 2. Решить неравенство х2 – 6х + 5![]() 0.
0.
Итоговый тест (8 кл)
Вариант 3
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Вычислите: ![]()
а) -47; б) 19; в) -767; г) 91.
А 2. При каком условии полное квадратное уравнение имеет два различных корня.
1) D=0 2) D>0 3) D<0
A3. Какое из чисел не входит в область определения выражения ![]() ?
?
а) 2; б) 0; в) -4; г) -2.
А 4. Найдите значение выражения: ![]()
а) 30; б) 40; в) 120; г) ![]()
А5. Произведение корней уравнения ![]() равно
равно
1) 5; 2) -5; 3) 25; 4) -25.
А 6. Решите уравнение 0,5у2 = 8
1) 2;-2; 2) 2; 3) 4;-4; 4) 4;
А 7. Найдите b в уравнении x2+bx-12=0,если оно имеет корень 4.
1) 1; 2) -1; 3) 7; 4) -7.
Часть В
К каждому заданию этой части записать краткий ответ.
B1. Найдите сумму большего и меньшего корней уравнения х2+5х-24=0.
B2. Одно число меньше другого на 4, а их произведение равно 221. Найдите эти числа.
B3. Разложите на множители х2 – 6х+9.
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1.Решите систему уравнений 
С 2. Решите уравнение
![]()
![]()
![]() =
=![]()
Итоговый тест (8 кл)
Вариант 4
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Найдите значение выражения: ![]()
а) ![]() ; б) 6,5; в)
; б) 6,5; в) ![]() ; г) 5,2.
; г) 5,2.
А 2. При каком условии полное квадратное уравнение не имеет корней.
1) D=0 2) D>0 3) D<0
A3. Какое из чисел не входит в область определения выражения ![]() ?
?
а) -6; б) 0; в) 4; г)8.
А 4. Найдите значение выражения: ![]()
а) 30; б) 40; в) 120; г) ![]()
А5. Произведение корней уравнения ![]() равно
равно
1) 5; 2) -5; 3) 25; 4) -25.
А 6. Решите уравнение 0,5у2 = 8
1) 2;-2; 2) 2; 3) 4;-4; 4) 4;
А 7. Найдите b в уравнении x2+bx-12=0,если оно имеет корень 4.
1) 1; 2) -1; 3) 7; 4) -7.
Часть В
К каждому заданию этой части записать краткий ответ.
B1. Найдите сумму большего и меньшего корней уравнения х2+5х-24=0.
B2. Одно число меньше другого на 4, а их произведение равно 221. Найдите эти числа.
B3. Разложите на множители х2 – 8х+16.
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1.Решите систему уравнений 
С 2. Решите уравнение ![]()
![]()
№ урока
Дата
Содержание урока
Кол-во часов
Прим.
Глава 1.Неравенства
19
раскрывают скобки; решают уравнения с одним неизвестным сводящиеся к линейным; записывают числа в стандартном виде; приводят подобные члены, выполняют действия с одночленами и многочленами; раскладывают многочлены на множители; выполняют совместные действия над алгебраическими дробями; решают системы двух уравнений с двумя неизвестными.
1,2
Положительные и отрицательные числа
2
3
Числовые неравенства
1
4,5
Основные свойства числовых неравенств
2
6
Сложение и умножение неравенств
1
7
Строгие и нестрогие неравенства
1
8
Неравенства с одним неизвестным
1
9-11
Решение неравенств
3
12
Системы неравенств с одним неизвестным. Числовые промежутки
1
13-15
Решение систем неравенств
3
16,17
Модуль числа. Уравнения и неравенства, содержащие модуль.
2
18
Обобщающий урок.
1
19
Контрольная работа по теме «Неравенства»
1
Глава 2. Приближенные вычисления
14
20,21
Работа над ошибками. Приближенные значения величин. Погрешность приближения.
2
Находят абсолютную погрешность приближения; находят приближенное значение с недостатком и с избытком; дают оценку абсолютной погрешности; округляют числа; находить относительную погрешность; записывают числа в стандартном виде; выполняют задания с применением правил сложения, вычитания, умножения и деления приближенных значений
22,23
Оценка погрешности
2
24
Округление чисел
1
25,26
Относительная погрешность
2
27,28
Простейшие вычисления на микрокалькуляторе
2
29,30
Стандартный вид числа. Проверочная работа.
2
31
Вычисления на микрокалькуляторе степени числа, обратного данному
1
32
Последовательное выполнение операций на микрокалькуляторе
1
33
Вычисления на микрокалькуляторе с использованием ячейки памяти
1
Глава 3. Квадратные корни
14
Вычисляют арифметический квадратный корень из чисел; записывают обыкновенные дроби в виде конечной или бесконечной периодической десятичной дроби; записывают бесконечные периодические десятичные дроби в виде обыкновенных; применяют теоремы о корне из степени, произведения, дроби при выполнении вычислений;
34,35
Арифметический квадратный корень.
2
36,37
Действительные числа
2
38-40
Квадратный корень из степени
3
41,42
Квадратный корень из произведения
2
43,44
Квадратный корень из дроби
2
45
Обобщающий урок
1
46
Контрольная работа по теме «Квадратные корни»
1
47
Работа над ошибками
1
Глава 4. Квадратные уравнения
23
Находят квадратные уравнения; решают неполные квадратные уравнения; выделяют полный квадрат; решают квадратные уравнения методом выделения полного квадрата; решают квадратные уравнения с помощью формулы корней квадратного уравнения общего вида; решают приведенные квадратные уравнения с использованием формулы корней и теоремы обратной теореме Виета;
48,49
Квадратное уравнение и его корни
2
50
Неполные квадратные уравнения
1
51
Метод вычисления полного квадрата
1
52- 55
Решение квадратных уравнений
4
56,57
Приведенное квадратное уравнение. Теорема Виета. Проверочная работа.
2
58-60
Уравнения, сводящиеся к квадратным
3
61-64
Решение задач с помощью квадратных уравнений
4
65-67
Решение простейших систем, содержащих уравнение второй степени
3
68
Обобщающий урок
1
69
Контрольная работа по теме
« Квадратные уравнения»
1
70
Работа над ошибками
1
Глава 5. Квадратичная функция
16
71
Определение квадратичной функции
1
распознают квадратичную функцию;
Находят нули функции; строят графики квадратичной функции; описывают свойства квадратичной функции;
72
Функция у =х 2
1
73-75
Функция у = ах 2
3
76-78
Функция у = ах 2 + bх + с
3
79-83
Построение графика квадратичной функции
5
84
Обобщающий урок
1
85
Контрольная работа по теме
« Квадратичная функция»
1
86
Работа над ошибками
1
Глава 6. Квадратные неравенства
12
Решают квадратное неравенство путем перехода к системе неравенств; решают неравенство с помощью графика; решают неравенства методом интервалов; исследуют квадратичную функцию.
87-88
Квадратное неравенство и его решение
2
89-93
Решение квадратного неравенства с помощью графика квадратичной функции
5
94,95
Метод интервалов
2
96
Исследование квадратного трехчлена
1
97
Обобщающий урок
1
98
Контрольная работа по теме
« Квадратные неравенства»
1
99,100
Повторение изученного материала за год
2
101
Итоговая контрольная работа
1
102
Итоговый зачет
1

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ