Чудаева Е.В., МОУ «Инсарская СОШ №1», г. Инсар, Республика Мордовия

РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ

(по материалам ЕГЭ)

Задача №1. Вычислите объём правильной треугольной пирамиды, если радиус описанной вокруг основания окружности равен , а высота пирамиды равна 4.

Задача №2. Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен , а боковые ребра пирамиды равны 6.

Задача №3. Вычислите площадь боковой поверхности правильной треугольной пирамиды, если радиус описанной около основания окружности равен , а высота пирамиды равны 1.

Задача №4. Вычислите объём правильной треугольной пирамиды, сторона основания которой равна 6, а апофема пирамиды равна .

Задача №5. Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен 2, а высота правильной пирамиды равна .

Задача №6. Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если её ребра равны 5, а радиус окружности, описанной вокруг основания равен 3.

Задача №7. В правильной четырехугольной пирамиде площадь боковой поверхности равна 16, а площадь основания 4. Найдите высоту пирамиды.

Задача №8. Вычислите объём правильной шестиугольной пирамиды, если сторона основания равна 4, а боковые ребра пирамиды равны 5.

Задача №9. В правильной шестиугольной пирамиде сторона основания равна 2, а боковое ребро равно 2. Найдите объём пирамиды.

Задача № 10. Около правильной треугольной призмы описан цилиндр. Высота цилиндра равна 5, а радиус его основания R удовлетворяет уравнению R² + R – 6 = 0. Найдите объём призмы.

Задача №11. Около правильной треугольной призмы описан цилиндр. Расстояние между осью цилиндра и стороной основания призмы равно . Высота цилиндра равна трем его радиусам. Найдите объём призмы.

Задача №12. Около правильной треугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 16 . Найдите объём призмы, если сторона её основания равна 5.

Задача №13. Около правильной четырехугольной призмы описан цилиндр, площадь боковой поверхности которого равна 20. Найдите площадь боковой поверхности призмы.

Задача №14. В правильную четырехугольную призму вписан цилиндр. Объем цилиндра равен 16 , а радиус окружности, описанной вокруг основания призмы, равен . Найдите диагональ призмы.

Задача №15. В правильную шестиугольную призму вписан цилиндр. Найдите высоту призмы, если её площадь равна 54 , а радиус цилиндра равен 3.

Задача № 16. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 16 , высота цилиндра равна 4. Найдите объём призмы.

Задача №17. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 10 . Найдите объём цилиндра, вписанного в эту же призму.

РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ

(по материалам ЕГЭ)

Задача №1. Вычислите объём правильной треугольной пирамиды, если радиус описанной вокруг основания окружности равен , а высота пирамиды равна 4.

Р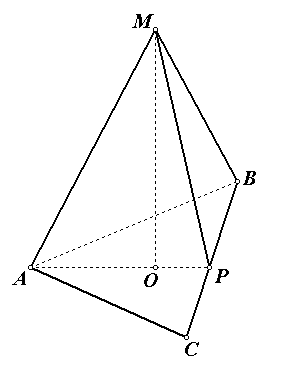ешение.

.

1) найдем сторону основания правильной пирамиды по формуле , .

2) найдем площадь основания, как площадь правильного треугольника , .

3) вычислим объём пирамиды

.

Ответ. 9

Задача №2. Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен , а боковые ребра пирамиды равны 6.

Решение.

1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда .

2) найдем сторону основания правильной пирамиды по формуле , .

3) найдем площадь основания, как площадь правильного треугольника , .

4) из прямоугольного треугольника по теореме Пифагора находим высоту пирамиды: , .

5) вычислим объём пирамиды

.

Ответ. 18.

Задача №3. Вычислите площадь боковой поверхности правильной треугольной пирамиды, если радиус описанной около основания окружности равен , а высота пирамиды равны 1.

Р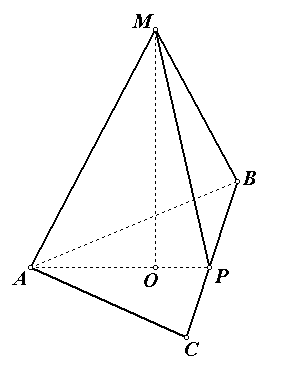ешение.

1) найдем сторону основания правильной пирамиды по формуле , .

2) найдем периметр основания Р = 3·а,

Р = 9.

3) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда .

4) из прямоугольного треугольника МОР по теореме Пифагора находим апофему МР: ,

МР =

5) вычислим площадь боковой поверхности правильной пирамиды:

,.

Ответ. .

Задача №4. Вычислите объём правильной треугольной пирамиды, сторона основания которой равна 6, а апофема пирамиды равна .

Решение. ,

1) найдем радиус описанной около основания и вписанной в основание окружностей: , то есть .

2) найдем площадь основания, как площадь правильного треугольника , .

3) из прямоугольного треугольника МОР по теореме Пифагора находим высоту: , МО = .

4) вычислим объём правильной пирамиды: = .

Ответ. 18.

Задача №5. Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен 2, а высота правильной пирамиды равна .

Решение.

1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда .

2) найдем сторону основания правильной пирамиды по формуле , .

3) найдем площадь основания, как площадь правильного треугольника , .

4) вычислим объём правильной пирамиды: = .

Ответ. 36.

Задача №6. Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если её ребра равны 5, а радиус окружности, описанной вокруг основания равен 3.

Р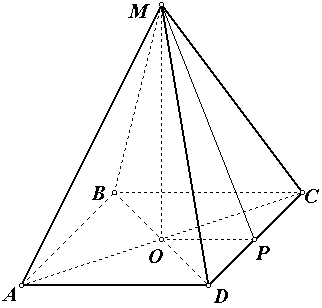ешение.

1) найдем сторону основания по формуле , т.е. .

2) найдем периметр основания: Р = 4а,

Р = 24.

3) из прямоугольного треугольника МDР по теореме Пифагора находим апофему МР: ,DP =

тогда: МР = .

4) вычислим площадь боковой поверхности пирамиды: = .

Ответ. 48.

Задача №7. В правильной четырехугольной пирамиде площадь боковой поверхности равна 16, а площадь основания 4. Найдите высоту пирамиды.

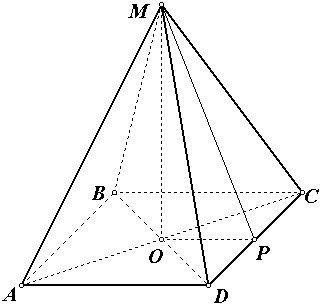
Решение.

1) найдем сторону основания: так как в основании пирамиды квадрат с площадью равной 4, то сторона квадрата равна 2, а его периметр 8.

2) по условию = 16 т.е.

.

3) из прямоугольного треугольника МОР по теореме Пифагора находим высоту: , учитывая, что ОР = = 1, получаем: МО = .

Ответ. .

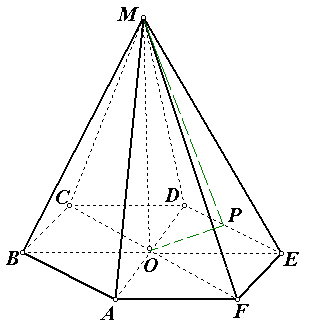
Задача №8. Вычислите объём правильной шестиугольной пирамиды, если сторона основания равна 4, а боковые ребра пирамиды равны 5.

Решение.

1) сторона основания правильного шестиугольника равна радиусу описанной около него окружности т.е. ,

2) площадь правильного шестиугольника найдем по формуле или = 24.

3) из прямоугольного треугольника МОВ найдем высоту МО: .

4) вычисляем объём пирамиды: =.

Ответ. 24.

Задача №9. В правильной шестиугольной пирамиде сторона основания равна 2, а боковое ребро равно 2. Найдите объём пирамиды.

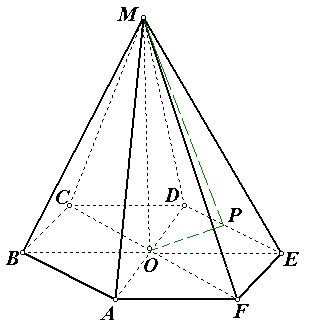
Решение.

1) найдем площадь правильного шестиугольника по формуле или = 12.

2) из прямоугольного треугольника МОВ найдем высоту МО, учитывая, что в правильном шестиугольнике : .

3) вычисляем объём пирамиды: =.

Ответ: 24.

Задача № 10. Около правильной треугольной призмы описан цилиндр. Высота цилиндра равна 5, а радиус его основания R удовлетворяет уравнению R² + R – 6 = 0. Найдите объём призмы.

Р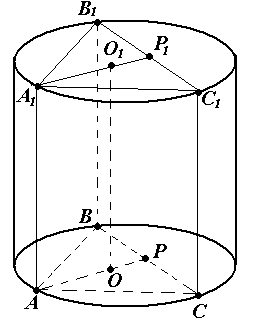ешение.V = S · H

1) так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, Н = 5.

2) по условию R удовлетворяет уравнению R² + R – 6 = 0, решая которое находим

R₁ = - 3, R₂ = 2, так как радиус величина положительная то -3 не удовлетворяет условию задачи.

3) найдем сторону вписанного правильного треугольника по формуле , .

4) найдем площадь основания правильной призмы, как площадь правильного треугольника: =
5) вычислим объём призмы: V = S · H = .

Ответ. 15.

Задача №11. Около правильной треугольной призмы описан цилиндр. Расстояние между осью цилиндра и стороной основания призмы равно . Высота цилиндра равна трем его радиусам. Найдите объём призмы.

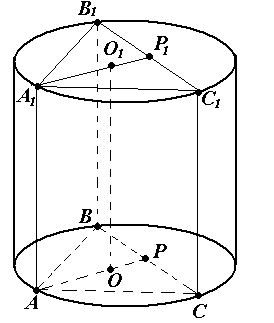
Решение. V = S · H

1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, по условию Н =3R..

2) Расстояние между осью цилиндра и стороной основания призмы равно радиусу вписанной в треугольник АВС окружности, т.е. , и по условию равно .

3) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда .

4) найдем сторону вписанного правильного треугольника по формуле , .

5) найдем площадь основания правильной призмы, как площадь правильного треугольника: =

6) вычислим объём призмы: V = S · H =S·3·R = 162.

Ответ. 162.

Задача №12. Около правильной треугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 16 . Найдите объём призмы, если сторона её основания равна 5.

Решение. V = S · H

1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра.

2) Найдем площадь основания правильной призмы, как площадь правильного треугольника: =.

3) Сторона вписанного правильного треугольника находится по формуле , тогда .

4) По условию площадь боковой поверхности цилиндра равна 16· т.е., откуда Н = = .

5) Вычислим объём призмы: V = S · H =·= 30.

Ответ. 30.

Задача №13. Около правильной четырехугольной призмы описан цилиндр, площадь боковой поверхности которого равна 20. Найдите площадь боковой поверхности призмы.

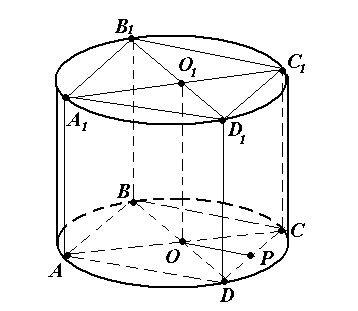Решение.

1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра.

2) По условию площадь боковой поверхности цилиндра равна 20, т.е. , .

3) так как призма правильная, то в её основании лежит квадрат, со стороной , тогда периметр основания равен .

4) вычислим площадь боковой поверхности призмы = .

Ответ. .

Задача №14. В правильную четырехугольную призму вписан цилиндр. Объем цилиндра равен 16 , а радиус окружности, описанной вокруг основания призмы, равен . Найдите диагональ призмы.

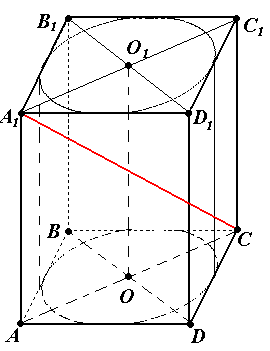
Решение. 1) Так как цилиндр вписан в призму, то высота призмы равна высоте цилиндра, а основание цилиндра вписано в основание призмы.

2) Так как радиус окружности, описанной вокруг основания призмы, равен =, то сторона квадрата равна

а радиус цилиндра равен, радиусу вписанной в квадрат окружности и равен:

3) По условию объём цилиндра равен 16, т.е. , = 4.

4) Из прямоугольного треугольника АСА₁ находим диагональ А₁С :

А₁С =.

Ответ. 8.

З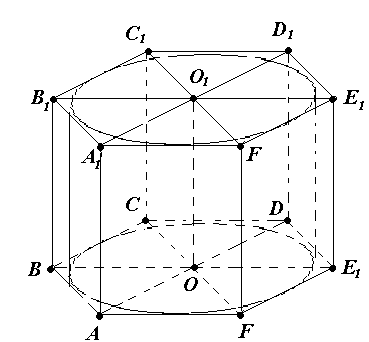адача №15. В правильную шестиугольную призму вписан цилиндр. Найдите высоту призмы, если её площадь равна 54 , а радиус цилиндра равен 3.
Решение.

1) Так как цилиндр вписан в призму, то высота призмы равна высоте цилиндра, а основание цилиндра вписано в основание призмы.

2) по условию радиус цилиндра равен 3, тогда , .

3) сторона правильного шестиугольника равна радиусу описанной около него окружности, т.е. .

4) по условию площадь призмы равна 54 , т.е.

P_осн.·Н + 2 S_осн=54.

5) найдем периметр основания и его площадь: Р = 6·а = 6 ·2=12.

S_осн = .

6) подставим полученные значения в формулу P_осн.·Н + 2 S_осн=54 и получим Н = (54 – 36 ): 12 =1,5.

Ответ. 1,5.

Задача № 16. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 16 , высота цилиндра равна 4. Найдите объём призмы.

Р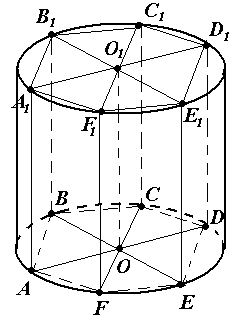ешение. V = S · H

1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, т.е. Н = 4.

2) по условию , т.е.

,R = 2.

3) так как сторона правильного шестиугольника равна радиусу описанной около него окружности, то а = 2.

4) Найдем площадь основания призмы по формуле:=6.

5) вычислим объём призмы: .

Ответ. 24.

Задача №17. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 10 . Найдите объём цилиндра, вписанного в эту же призму.

Решение. V = S · H

1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра.

2) по условию , т.е.

.

3) так как сторона правильного шестиугольника равна радиусу описанной около него окружности, то R = а.

4) выразим радиус основания вписанного цилиндра через радиус описанного цилиндра: .

5) запишем формулу вычисления объёма вписанного в призму цилиндра: V = S · H, т.е.:

V = =·.

Ответ. 7,5.