Урок для 10 класса по теме: "Функция y=sin x ее свойства и график"
М![]() униципальное бюджетное общеобразовательное учреждение
униципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 47 с углубленным изучением отдельных предметов
городского округа Тольятти
Урок алгебры и начала анализа
Учитель математики МБУ СОШ № 47 Автозаводского района г.о. Тольятти
Дьячкова Светлана Николаевна
Класс: 10 «А»
Тип урока: объяснение нового материала.
Модель урока: интегрированный с информатикой и ИКТ
Технология: личностно-ориентированная с применением ИКТ технологий.
Тема: Функция y=sin x ее свойства и график.
Цель урока: изучить построение графика функции y=sinx, рассмотреть построение графиков тригонометрических функций, задаваемых формулами вида y=sinx+n, y=Аsinx , y=sin(x-m ), y=sinkx с помощью программы Microsoft Office Excel.
Задачи урока:
Обучающая: познакомить с основными свойствами функции y=sin x, отработать алгоритм работы с таблицей и диаграммой в программе Microsoft Office Excel при построении тригонометрической функции, повторить основные свойства изученных функций.
Развивающая: уметь соотносить изучаемые функции с конкретной и жизненной ситуацией, развивать наглядно-образное и наглядно – действенное мышление, уметь работать по инструкции.
Воспитательная: ориентировать на профессиональный выбор, профессию.
Оборудование: компьютерный класс, проектор, операционная система Windows, пакет Microsoft Office.
Ход урока.
Организационно-мотивационный момент-7 минут
Приветствие. Сообщение цели урока. Инструктаж по технике безопасности при работе с компьютером.
Цель этапа: постановка задачи и мотивация на дальнейшую деятельность обучающихся на уроке.
1.1. Слово учителя математики:
-Здравствуйте ребята, сегодня мы повторим все известные вам функции и изучим новую функцию y=sin x, построим график ее с помощью программы Microsoft Office Excel. Но для начала вспомним правила работы за компьютером в школе (проведение инструктажа по технике безопасности).
1.2. Стартовая презентация учителя математики в программе Microsoft Office PowerPoint и постановка проблемных вопросов для обучающихся:
Какие кривые существуют вокруг нас?
Какая кривая называется линией жизни. Какие свойства у линии жизни?
Гармоническое колебание линии жизни.
Расчет биоритмов человека с помощью ИКТ технологий.
Цель: повторить основные свойства изученных функций, обобщить знания ребят по теме «Функция» и ввести в новую тему урока, развивать умение соотносить изучаемые функции с конкретной и жизненной ситуацией.
Беседа сопровождается наглядным материалом презентации. На экране всевозможные фотографии из жизни «Кривые вокруг нас», ученик должен увидеть на график какой функцию похоже изображение вспомнить ее свойства, перечислить и ответить на вопрос:
-Какие кривые существуют вокруг нас?






В конце показа приходим к функции y=sin x, мы видим на фото хребет гор и кардиограмму сердца больного с учащенным биением ритма. И задаем вопрос, какую функцию вы видите здесь- «Линия жизни», и мы переходим к следующему этапу изучение новой темы, а, именно, задаем новый вопрос: Какая кривая называется линией жизни. Какие свойства у линии жизни?
Объяснение нового материал-10 минут.
Цель: познакомить с основными свойствами функции y=sin x, отработать алгоритм работы с таблицей и диаграммой в программе Microsoft Office Excel при построении тригонометрической функции.
Слово учителя математики. Практическая работа обучающихся.
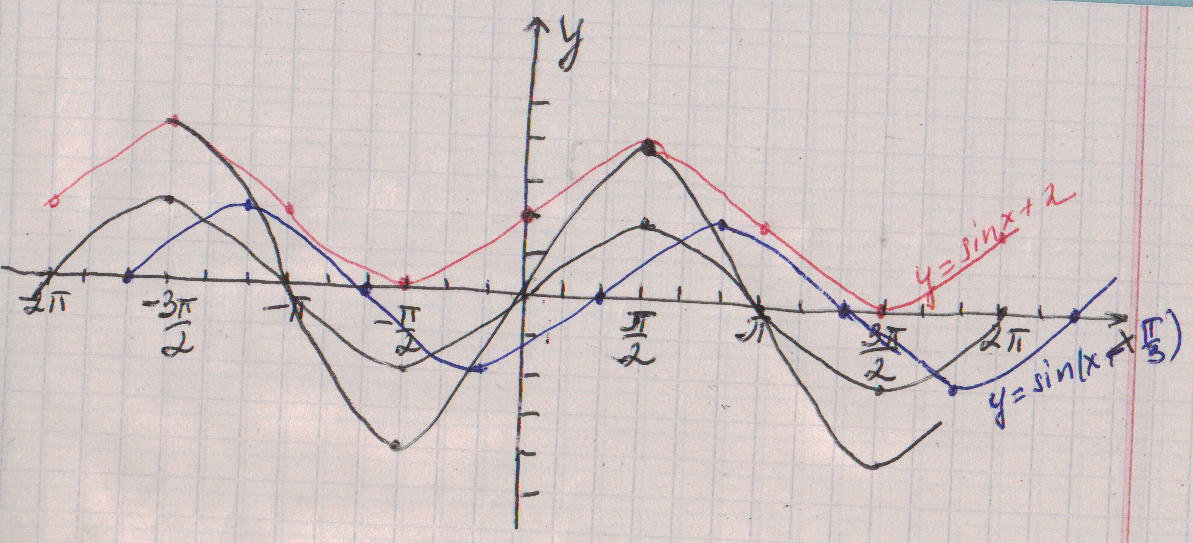
Кривая линия жизни очень похожа на график функции у=sin x. Определение: числовая функция, заданная формулой у=sin x, называется синусом. График такой функции является синусойда. Используя единичную окружность и таблицу значений синуса, построим в тетради график данной функции.
-Но для начала подумаем, а какова будет область определения данной функции?
-Область значений?
-Установите четность, нечетность функции?
В тетради постройте систему координат. Учитывая, что область определения синуса промежуток от -1 до 1, ось y разместим на 10 клетках. Ось х растянем на ширину тетрадного листа. За единичный отрезок по оси х возьмем 1 см. Учитывая, что p»3,14, и округляя это число до целых, на оси х за p возьмем 6 клеток. Отметим узловые точки и табличные значения синуса. Выполним преобразование симметрии относительно прямой x=p/2, относительно точки (p, 0). Соединим полученные точки и продолжим график с учетом периодичности функции, учитывая что sin (x+2пn)=sin x.

Оперирование полученными знаниями в новой ситуации-13 минут.
Цель этапа: рассмотреть построение графиков тригонометрических функций, задаваемых формулами вида y=sinx+n, y=Аsinx , y=sin(x-m ), y=sinkx с помощью программы Microsoft Office Excel, формировать умение действовать по инструкции.
3.1.Слово учителя математики. Актуализация ранее полученных знаний по теме «Движение функции».
А теперь ответим на вопрос: «Гармоническое колебание линии жизни».
Учитель: Сколько и какие существуют преобразования графика функции y=f(x)?
y=f(x)+b, b–число. Параллельный перенос графика вдоль оси ординат на вектор
(0;b). Если b>0 – перенос вверх, b<0 – перенос вниз.y=kf(x). Расширение графика вдоль оси ординат в. Если |k|<1, то растяжение с коэффициентом k называют сжатием в
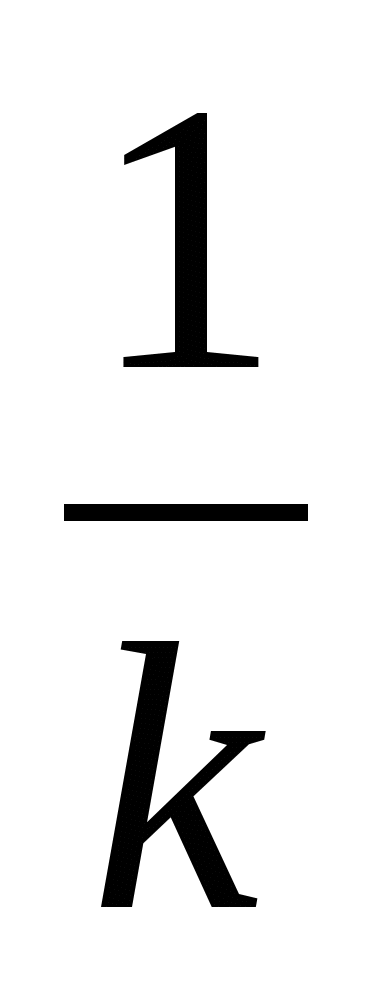 раз.
раз. y=f(x–a). Параллельный перенос графика вдоль оси ординат на вектор
(a;0).Если а>0 – перенос вправо, а<0 – перенос влево.y=f(
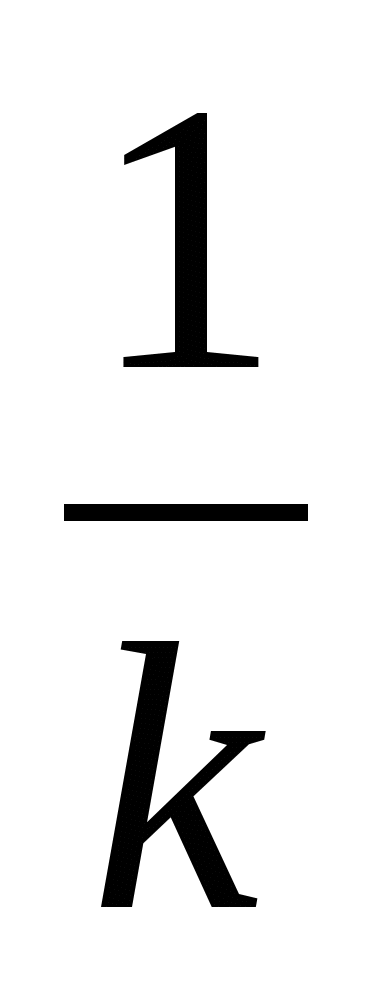 ). Растяжение графика вдоль абсцисс. Если |k|<1, то растяжение с коэффициентом k называют сжатием в
). Растяжение графика вдоль абсцисс. Если |k|<1, то растяжение с коэффициентом k называют сжатием в 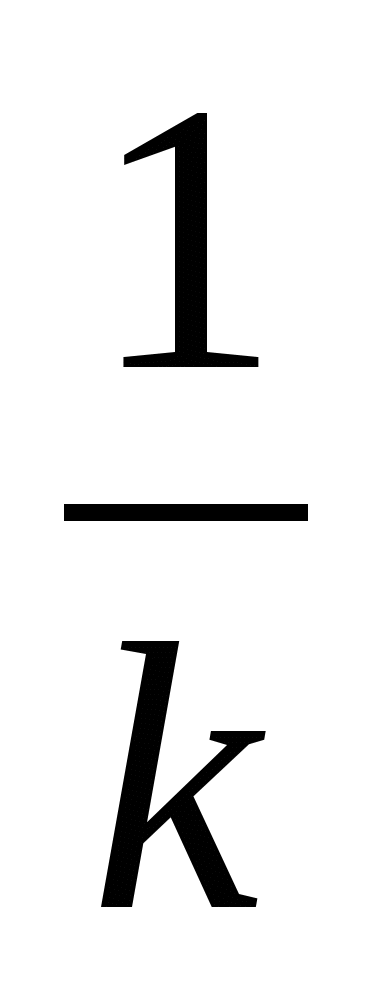 раз.
раз. y=–f(x). Симметрия графика относительно оси ординат.
y=f(–x). График симметричен относительно оси абсцисс.
y=|f(x) |. Часть графика при y0 сохраняется, а часть графика при y<0 отображается симметрично относительно оси абсцисс.
y=f(|x|). Часть графика при x0 сохраняется, часть при x<0 – отображается симметрично относительно оси ординат.
Учитель: Какая команда меню позволяет строить диаграммы и графики в табличном процессоре Ехсе1? Ответ учеников: Мастер диаграмм.
Учитель: Как задается вычисление в таблице значений ячеек по формуле? Ответ учеников: Ввести знака «=», активизация нужной ячейки, содержимое которой будет являться аргументом, ввод соответствующих функций и знаков арифметических операций. Ввод формулы можно контролировать с помощью окна ввода формулы.
Учитель: Как можно скопировать формулу в несколько ячеек? Ответ учеников: С помощью маркера автозаполнения в правом нижнем углу курсора или с помощью команды Правка – Копировать и Правка – Вставить.
Учитель: Как сделать ссылку абсолютной для того, чтобы при копировании она не изменялась? Ответ учеников: Необходимо установить перед именем столбца и строки знак «$».
3.2 Самостоятельная работа обучающихся за компьютером. Действие по инструкции.
Класс делится на четыре варианта и каждый получает задание. Получившиеся графики отражаются на экране.
Построить график функции y=кsin x,
Построить график функции y=sin x+в,
Построить график функции y=sin (x+с),
Построить график функции y=sin (x+с)+в,
Инструкционная карта для построения y=sin x:
Заполнение таблицы зависимости y(x)
1. Запустите среду MS Excel. Выполните команду Файл-Открыть… Выберите в окне файлера Windows файл «График тригонометрической функции.xlt» из папки Общие документы.
2. Занесите исходные числовые данные в следующие ячейки:
D10 – левая граница области построения (введите -12)
D11 – правая граница области построения (введите 12)
D12 –число столбцов (20 штук)
D13-шаг=0,4
3. Таблица данных содержит пару колонок Абсцисса (F5) и Ордината G(5). Заполним таблицу:
скопируйте в ячейку F5 содержимое ячейки D10 (левая граница области построения): введите формулу в ячейку F5: =D10;
в ячейке F6 произведите расчет следующего значения абсциссы. Ввести формулу в ячейку F6: =F5+$D$13;
скопируйте формулу из ячейки F6 в диапазон ячеек F7:F40. Колонка Абсцисса заполнена.
в диапазон ячеек G5:G40 занесите формулы, позволяющие рассчитать значение функции в каждой точке: введите формулу в ячейку G5: =sin(F5), скопируйте формулу в ячейки G5:G40;
Измените имя листа на Тригонометрическая функция.
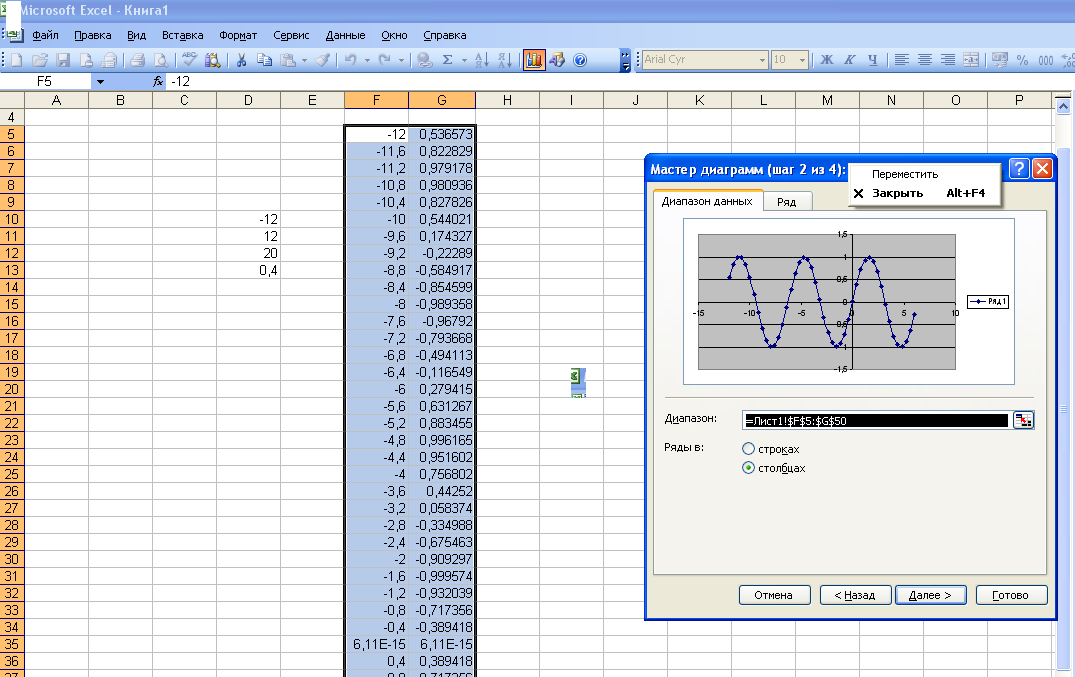
Построение графика зависимости y(x)
Таблица данных содержит один ряд данных F5:G40 для построения графика вида y=f(x).
1. Выделите диапазон ячеек F5:G40, содержащий данные для построения графика. 2. Выберите команду Вставка-Диаграмма…
Шаг 1. В диалоговом окне Тип диаграммы выберите тип диаграммы Точечная, вид «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров», нажмите кнопку Далее.
Шаг 2. В окне Источник данных диаграммы на вкладке Диапазон данных проверьте, что диапазон выбран правильно и установлен флажок опции «Ряды в столбцах».
Шаг 3. Задайте параметры диаграммы (окно Параметры диаграммы): на вкладке Заголовки введите:
– в поле Название диаграммы – «График показательной функции»
– в поле Ось Х (категорий) – «x»;
– в поле Ось Y (значений) – «y»;
На вкладке Линии сетки отключите основные и промежуточные линии сетки по каждой из осей. На вкладке Легенда уберите флажок Добавить легенду. Нажмите кнопку Далее.
Шаг 4. Выберите расположение диаграммы на отдельном листе и введите имя листа График в соответствующем поле. После этого нажмите кнопку Готово.
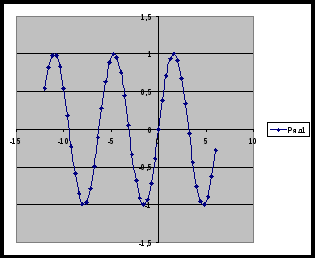
Инструкционная карта «Преобразование графика тригонометрической функции»:
Для построения графика функции y=кsin x, в диапазон ячеек G5:G40 занесите формулы, позволяющие рассчитать значение функции в каждой точке: введите формулу в ячейку (в зависимости от задания) G5: =к*sin(F5) или G5: =sin(F5+с) или G5: =(sin(F5)) +в или G5: =(к*sin(F5+с))+в где к, с, в действительные числа, скопируйте формулу в ячейки G5:G40.
Далее по инструкции «Построение графика зависимости y(x)» проделайте те же шаги.
Презентация групп. Описание свойств функции по каждому графику.
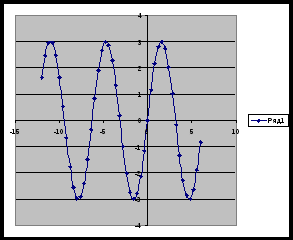
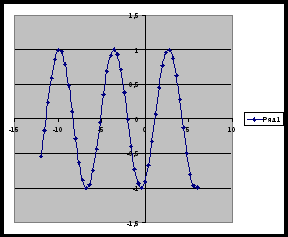
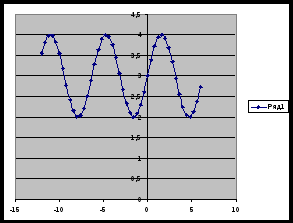
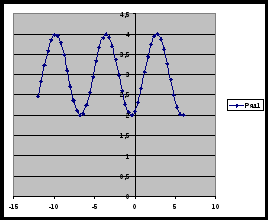
Вывод: график функции y=sin x совершает гармонические колебания: движения по осям координат.
Пронаблюдав движение графика с помощью компьютерной программы, ребята строят графики функций y=2sin x, =sin x+2, y=sin (x-п/3) в тетради, учитывая, что п=6 клеток. п/2=3 клетки, п/3=2 клетки и правила движения функции по осям координат.
4.Первичное закрепление полученных знаний-7 минут.
Цель этапа: уметь соотносить изучаемые функции с конкретной и жизненной ситуацией, развивать наглядно-образное и наглядно – действенное мышление, ориентировать на профессиональный выбор, профессию.
Слово учителю математики:
Синусоида была первым графиком тригонометрических функций. Этот график был вычерчен в конце 30-х годов XVII в. французским математиком Жюлем Робельвалем . Где же в жизни мы встречаемся с такими функциями и существуют ли вообще их применение? По закону синуса происходят гармонические колебания. Примером таких колебаний является движение маятника или шарика, подвешенного на пружинке, частота звука также описывается законом синуса. Гармонические колебания – это колебания, при которых изменение смещения во времени происходит по закону функции синус. Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII Леонардом Эйлером. Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д.. Поэтому тригонометрические функции всесторонне и глубоко исследовались и приобрели важное значение для всей математики и для других наук. Итак давайте ответим на вопрос последний сегодняшнего урока: Расчет биоритмов человека с помощью ИКТ технологий
Китайский ученый Кай Цун разработал в 19 веке формулу подсчета собственных биоритмов человека. Каждый человек ежемесячно выстраивать с помощью тригонометрической функции y=sin x свой график интеллектуальной, эмоциональной и физической кривой. Увидеть когда у человека «взрыв» деятельности, а когда спад. Предлагается каждому учащемуся выстроить свои кривые на данный месяц с помощью компьютера.
Самостоятельная работа обучающихся, ориентированная на закрепление полученных знаний о построении функции и ее свойств.
Формула y=аsin (х+Т)/n+3,1, где a –число месяца, х- число лет человеку, Т- количество дней в данном месяце, п –календарный год.
Тетрадь ученика.
Подведение итогов урока. Оценочная часть- 3 минуты.
Беседа
Какие свойства у линии жизни?
Как происходит гармоническое колебание линии жизни?
Каково практическое применение тригонометрической функции?
Выставление оценок обучающимися проявивших себя в умении читать и строить график функции y=sin x с учетом движения и помощью программы Microsoft Office Excel. Рефлексия.
Домашнее задание:
на оценку «3» выполнить задание по учебнику № 36, (а,б), 37 (а,б) № 33 (а)
на оценку «4» дополнительно построить график функции y=2 sin(0,5x–p/6)+1 с помощью компьютера, сохранить данные на листе и выполнить скриншет данной странице, показать его учителю.
на оценку «5» выполнить данные задания и сделать подбор физических или химических, экономических задач, где используется функция y=sin x.


Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ