Алгоритмы вывода кинетических уравнений для стационарных и квазистационарных процессов
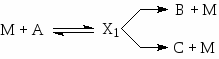
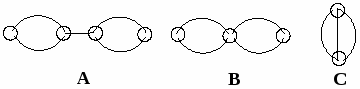
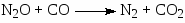
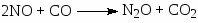
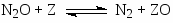
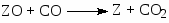
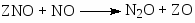
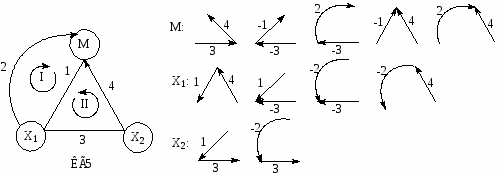 Алгоритмы вывода кинетических уравнений для стационарных и
Алгоритмы вывода кинетических уравнений для стационарных и
квазистационарных процессов
Используя соотношения (51) и (57), можно получить выражение для скорости любой стадии механизма (алгоритм Мезона).
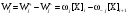
Для каталитической реакции
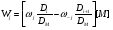 или (61)
или (61)
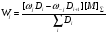 (62)
(62)
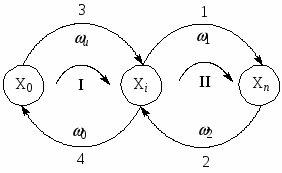
Для графов механизмов с висячими вершинами
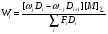 (63)
(63)
Деревом называется любая последовательность дуг графа, не содержащая циклов. Максимальным деревом (или каркасом) называют последовательность дуг, проходящую через все вершины и не содержащую циклов. Корневым деревом, или деревом, имеющим корень в вершине i (каркас вершины i), называют максимальное дерево, все дуги которого направлены к вершине i. Для КГ5 двухмаршрутной каталитической реакции приведены корневые деревья для вершин М, X1 и X2.
Теперь определим вес корневого дерева Dik как произведение весов дуг (k-тое дерево в i-той вершине)
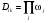 (j {i, k}) (48)
(j {i, k}) (48)
Корневой определитель Di вершины i есть сумма весов корневых деревьев (сумма весов каркасов) вершины i
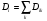 (49)
(49)
Предложено несколько методов определения величин Di (и всех Dik). Простейший алгоритм (Л.Г. Брук) сводится к следующим операциям. Определим 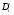 как произведение сумм весов дуг, выходящих из всех вершин, кроме i-той. Например, для вершины М в КГ5 (
как произведение сумм весов дуг, выходящих из всех вершин, кроме i-той. Например, для вершины М в КГ5 (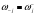 ,
, 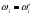 )
)
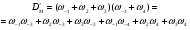
Исключим из 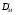 произведение весов, образующих цикл (контур), включая произведения весов прямых и обратных стадий (3–3). В результате получим
произведение весов, образующих цикл (контур), включая произведения весов прямых и обратных стадий (3–3). В результате получим
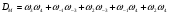
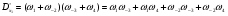
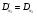
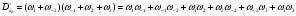
Удалим циклы 12, 1–1 и 2–2, –1–2.
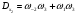
Как известно, общий метод вывода уравнения скорости по маршруту (по итоговому уравнению маршрута) для стационарных и квазистационарных реакций сводится к нахождению выражений для концентраций интермедиатов Xi в результате решения системы линейных алгебраических уравнений 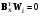 для линейно независимых Xi. Система уравнений решается по правилу Крамера (см. выше)
для линейно независимых Xi. Система уравнений решается по правилу Крамера (см. выше)
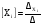 (50)
(50)
где – определитель системы линейных уравнений, записанный для коэффициентов при неизвестных, 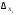 – определитель, в котором столбец коэффициентов при Xi заменен на столбец постоянных свободных членов.
– определитель, в котором столбец коэффициентов при Xi заменен на столбец постоянных свободных членов.
Как мы уже упоминали, Кинг и Альтман впервые применили метод графических диаграмм для нахождения определителей 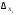 и . Общее правило, позволяющее использовать графы для решения проблем, связанных с линейными законами типа y = ax, было сформулировано Мэзоном и использовано для решения систем уравнений Кирхгофа в теории электрических цепей (х – сила тока, а – сопротивление, у – разность потенциалов).
и . Общее правило, позволяющее использовать графы для решения проблем, связанных с линейными законами типа y = ax, было сформулировано Мэзоном и использовано для решения систем уравнений Кирхгофа в теории электрических цепей (х – сила тока, а – сопротивление, у – разность потенциалов).
Суть этого правила выражается соотношением (51)
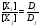 (51)
(51)
Применительно к кинетике реакций с линейным механизмом величина х в линейном законе у = ах – концентрация i-того интермедиата, а – вес стадии 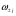 , у – скорость стадии
, у – скорость стадии 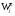 . Это правило было использовано по аналогии Волькенштейном и Гольдштейном для вывода кинетических уравнений скорости ферментативных реакций методом графов. В работах Яблонского и сотр. доказано соотношение (51), и показана его связь с правилом Крамера. Если
. Это правило было использовано по аналогии Волькенштейном и Гольдштейном для вывода кинетических уравнений скорости ферментативных реакций методом графов. В работах Яблонского и сотр. доказано соотношение (51), и показана его связь с правилом Крамера. Если 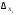 и записать через веса стадий, а в случае каталитической реакции вынести из
и записать через веса стадий, а в случае каталитической реакции вынести из 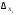 концентрацию катализатора ([М], КГ5), получим:
концентрацию катализатора ([М], КГ5), получим:
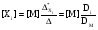 , (52)
, (52)
где Di = 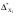 , DM =
, DM =
Из (50) и (52) получаем также
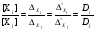 (53)
(53)
В случае некаталитических реакций концентрация Xi запишется через концентрацию нуль-вещества в нуль-вершине графа
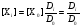 (54)
(54)
Если все [Xi] в каталитической реакции выразить через [М], получим выражение для суммарной концентрации катализатора
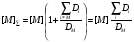 (55)
(55)
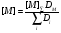 (56)
(56)
Из (52) и (56) получаем
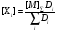 (57)
(57)
В гетерогенных процессах при нормировке всех Xi к [Х] (выражение [Xi] через доли поверхности 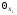 ) получаем
) получаем
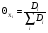 (58)
(58)
Есть два способа учесть наличие висячих вершин в материальном балансе по катализатору. Найдя корневые определители для висячих вершин, их следует включить в 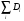 , тогда [М] будет включать и соединения, находящиеся в висячих вершинах. Поскольку ребра графа, инцидентные висячим вершинам, в случае стационарных и квазистационарных процессов являются равновесными стадиями, можно ввести дополнительную функцию – закомплексованность интермедиата (любой вершины циклического графа)
, тогда [М] будет включать и соединения, находящиеся в висячих вершинах. Поскольку ребра графа, инцидентные висячим вершинам, в случае стационарных и квазистационарных процессов являются равновесными стадиями, можно ввести дополнительную функцию – закомплексованность интермедиата (любой вершины циклического графа)
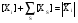
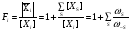 (59)
(59)
где [XS] – концентрация соединения в висячей вершине графа, связанной с графом стадией S, S и –S – веса стадии, инцидентной висячей вершине и направленной от Xi к XS. Очевидно, что отношение 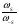 включает константу равновесия KS и концентрации участников реакции, входящие в S и –S. Так, для вершины М в графе КГ4 получим
включает константу равновесия KS и концентрации участников реакции, входящие в S и –S. Так, для вершины М в графе КГ4 получим
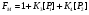
Формула (57) может быть модифицирована, поскольку 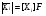 ,
,
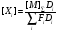 (60)
(60)
По уравнению стационарности стадий 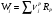 легко установить связь скорости стадии со скоростью по маршруту, и таким образом найти RP. При отсутствии висячих вершин Fi = 1.
легко установить связь скорости стадии со скоростью по маршруту, и таким образом найти RP. При отсутствии висячих вершин Fi = 1.
Другой алгоритм был предложен Волькенштейном и Гольдштейном и модифицирован Яблонским и сотрудниками. На графе многомаршрутной реакции выбирается стадия, принадлежащая одному из маршрутов (Wj = RP), и скорость этой стадии записывается уравнением (64)
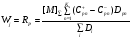 , (64)
, (64)
(или через FiDi для случая с висячими вершинами)
где 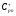 – вес n-ого цикла по маршруту Р, включающего стадию j, Dpn – определитель подграфа, получающегося при сжатии n-ого цикла по маршруту Р в одну вершину с корнем в полученной при сжатии вершине, К – число циклов, проходящих через стадию j.
– вес n-ого цикла по маршруту Р, включающего стадию j, Dpn – определитель подграфа, получающегося при сжатии n-ого цикла по маршруту Р в одну вершину с корнем в полученной при сжатии вершине, К – число циклов, проходящих через стадию j.
Если скорость по маршруту Р описывается комбинацией скоростей стадий Wj, то уравнение (64) записывается для всех стадий.
Пример 8. Рассмотрим КГ5. Из графа видно, что базис маршрутов включает два маршрута (два простых цикла). Выберем эти простые циклы в качестве базиса. Первый маршрут включает стадии 1 и 2, второй – 1, 3, 4. Из КГ5 с очевидностью следует, что W2 = R1 и W4 = R2. Естественно, что и W3 = R2, но для упрощения вывода возьмем необратимую стадию 4. По второму алгоритму запишем величины циклов Сpn.
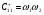 ;
;
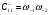
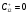 (
(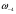 = 0);
= 0);
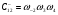
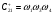 ;
;
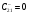
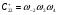 ;
; 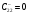 .
.
Запишем величины подграфов Dpn: D11 = –3 + 4 (сумма весов деревьев, входящих в вершину, полученную при сжатии цикла 11), D12 = 1 (одной вершине соответствует Dpn = 1), D21 = 1 и D22 = 1. Используя величины DM, 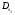 и
и 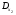 , найденные выше, запишем выражения для R1 и R2:
, найденные выше, запишем выражения для R1 и R2:
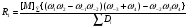 (64)
(64)
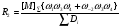 (65)
(65)
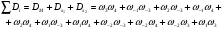
Для одномаршрутной реакции скорость стадии 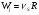 , а в случае линейного механизма S = 1. Следовательно
, а в случае линейного механизма S = 1. Следовательно
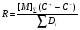 (66)
(66)
Полезно отметить, что в этом случае циклическая характеристика С = С+ – С– соответствует закону действия масс, записанному для итогового уравнения одномаршрутной реакции как элементарной стадии.
Пример 9.
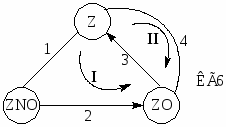
Механизм реакции изобразим КГ6:
(1)
(2)
(3)
(4)
Стехиометрический анализ механизма привел к матрице Г для Р = 2 с соответствующим набором независимых итоговых уравнений (P = 2)
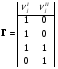
I)
II)
На КГ6 указаны эти маршруты, соответствующие двум минимальным циклам КГ6. При сложении двух векторов получим маршрут NII* (1 1 2 1) с уравнением 2NO + 2CO N2 + 2CO2, а при вычитании – маршрут NII** (1 1 0 –1), включающий цикл из 1, 2 и 4 стадий: 2NO + N2 2N2O. Из условия стационарности стадий (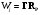 ) и КГ6 следует, что
) и КГ6 следует, что
W1 = R1, W2 = R1, W3 = R1 + R2, W4 = R2
(для маршрутов I и II)
Используем алгоритмы Яблонского (64) и Мезона (62). Для обоих уравнений нужны величины Di. Запишем для каждой вершины i произведения сумм весов стадий, выходящих из всех других вершин КГ j i. Перемножим скобки и исключим из полученных сумм произведения стадий, образующих цикл, включая произведения 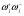 . В результате получим Di. Для графа КГ6 запишем произведения сумм весов стадий:
. В результате получим Di. Для графа КГ6 запишем произведения сумм весов стадий:
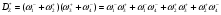
Здесь нет циклов и 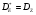 .
.
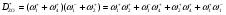
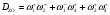
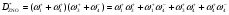
Здесь два цикла 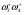 и
и 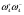 . Поэтому исключим их:
. Поэтому исключим их:
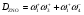
Таким образом, в КГ6 девять деревьев, величины которых войдут в Di.
Для использования уравнения (64) надо найти величины циклов Сpn, проходящих через стадию, определяющую скорость RP (p – номер маршрута, n – номер цикла), и величины подграфов Dpn, которые являются корневыми определителями графов в вершине pm, образующихся при сжатии цикла n в одну вершину pn. В случае, когда после сжатия цикла остается одна вершина Dpn = 1. Итак, выбираем R1 = W2 и R2 = W4. В реакциях на поверхности [M] = 1 (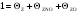 ).
).
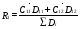 (67)
(67)
Величина цикла равна произведению весов стадий. Тогда:
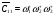 D11 = 1
D11 = 1
 D12 = 1
D12 = 1
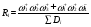 (68)
(68)
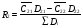 (69)
(69)
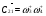
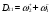
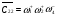 D22 = 1
D22 = 1
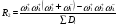 (70)
(70)
Получим уравнение для R2 по правилу Мезона (62), т.е. уравнение идентичное уравнению (70).
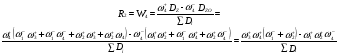
Топология механизма и особенности кинетической модели
Структура КГ (топологический тип механизма) сильно влияет на вид кинетического уравнения, степень его сложности, число комплексов констант скорости и число констант скорости в числителе и знаменателе кинетического уравнения. Например, для Р = 2 имеем 3 топологических класса с заметно различными кинетическими моделями.
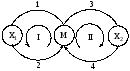 Рассмотрим два механизма классов В и C с Р = 2, S = 4, I = 3.
Рассмотрим два механизма классов В и C с Р = 2, S = 4, I = 3.
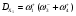
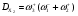
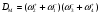
КГ 7
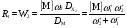 (71)
(71)
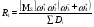 (72)
(72)
Разделим Di и числитель на DM:
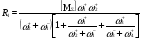 (73)
(73)
Из уравнений (71 – 73) видно, что скорости маршрута II входят в R1 только за счёт закомплексованности катализатора FM (член в квадратных скобках), где: 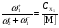 ,
, 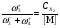 . В случае использования величины [M] уравнение (71) описывает скорость по маршруту I без какого-либо влияния стадий маршрута II. Если сложность модели оценить числом К* констант скорости, входящих во все слагаемые числителя и знаменателя кинетического уравнения, то
. В случае использования величины [M] уравнение (71) описывает скорость по маршруту I без какого-либо влияния стадий маршрута II. Если сложность модели оценить числом К* констант скорости, входящих во все слагаемые числителя и знаменателя кинетического уравнения, то 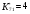 , а
, а 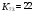 .
.
Механизм класса С представлен на КГ 8:
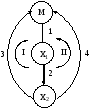
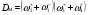
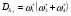
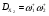
КГ 8
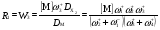 (74)
(74)
Отметим сразу, что для структуры КГ 8 и в случае [M] характерно участие стадий маршрута II в уравнении для R1. Величина 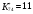 .
.
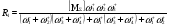 (75)
(75)
В уравнении (75) 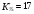 . Здесь не столь большое увеличение К* при переходе от [М] к [М]. Степень сложности механизма, степень связанности графа является важным для дискриминации гипотез фактором.
. Здесь не столь большое увеличение К* при переходе от [М] к [М]. Степень сложности механизма, степень связанности графа является важным для дискриминации гипотез фактором.
Для КГ 9, отражающего механизм цепного процесса, получим более простые соотношения для скоростей I и II маршрутов, зависящих от [Х0] (инициатора).
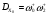
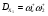
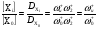
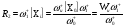
Скорость второго маршрута включает стадии первого маршрута и концентрацию, стоящую в первой вершине Х0.
Вопросы для самоконтроля
Приведите алгоритм использования правила (метода) Хориути для нахождения итоговых уравнений маршрутов.
Как связаны скорости по маршрутам со скоростями стадий и скоростями по веществам?
Как связаны скорости по веществам со скоростями стадий? Смысл условия квазистационарности Боденштейна.
Приведите соотношения основных базисов в стехиометрии реакций и в теории маршрутов.
На каком соотношении основано применение теории графов для вывода кинетических уравнений?
Запишите материальный баланс по катализатору для реакции с линейным механизмом методом теории графов.
Примените условие стационарности стадий для вывода кинетического уравнения двухмаршрутной реакции с тремя стадиями
Литература для углубленного изучения
Темкин О.Н., Кинетика каталитических реакций в растворах комплексов металлов, М., МИТХТ, 1980, ч. II (учебное пособие).
Яблонский Г.С., Быков В.И., Горбань А.Н., Кинетические модели каталитических реакций, Наука, СО, Новосибирск, 1983.
Киперман С.Л., Основы химической кинетики в гетерогенном катализе, М., Химия, 1979.
Темкин О.Н., Одинцов К.Ю., Брук Л.Г., Приближения квазистационарности и квазиравновесия в химической кинетике, М., МИТХТ, 2001, 78 с. (учебное пособие).
Темкин О.Н., Брук Л.Г., Бончев Д., Топологическая структура механизмов сложных реакций, Теоретич. и эксперимент. химия, 1988, №3, с. 282.
Temkin O.N., Bonchev D., Application of Graph Theory to Chemical Kinetics, J. Chem. Education, 1992, v. 92, p. 544 – 550.
Temkin O.N., Zeigarnik A.V., Bonchev D.G., Chemical Reaction Networks. A Graph-Theoretical Approach. CRC Press, Boca Raton, USA, 1996, 286 p.
Горский В.Г., Швецова-Шиловская Т.Н., Петрунин В.А., Феноменологическая и стационарная кинетика сложных химических реакций, Ойкумена, 2002, 407 с.

Нравится материал? Поддержи автора!
Ещё документы из категории химия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ