Федеральное агентство по образованию

ГОУ ВПО «Уральский государственный технический университет – УПИ»

Факультет информационно-математических технологий и экономического моделирования

Кафедра анализа систем и принятия решений

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ИНВЕСТИЦИОННЫХ РИСКОВ

Курсовая работа

дисциплина: «Имитационное моделирование экономических процессов»

Руководитель: Бородачёв С. Н.

Нормоконтролер: Медведева М. А.

Студент группы ИМ-37012 Косарев А.И.

Екатеринбург

2009

Содержание

Введение

Мой вариант курсовой работы №12. Суть моего задания заключается в том, чтобы рассчитать оценки NPV, математического ожидания, дисперсии, и статистических отклонений при условии случайного распределения исходных данных. Требуется с использованием программы MathCAD решить данную задачу и сравнить полученные результаты с результатами лекционного примера. Для этого нам нужно определить, что за программу мы должны написать в MathCAD для получения требуемых результатов. Для этого требуется построить блок-схему. По итогу нужно заключить какие параметры изменились, насколько они отличаются от лекционного примера и почему.

Раздел 1. Постановка задачи

Моё задание по курсовой работе (Вариант 12) :

Имитационное моделирование инвестиционных рисков (обобщение: считать Q,P,V дискретными случайными величинами).

Показатели

Наихудший

Наилучший

Вероятный

Q

150

300

200

P

40

55

50

V

38

25

30

Рассчитать средние и дисперсии показателей и использовать их в нормальной аппроксимации распределения соответствующих величин.

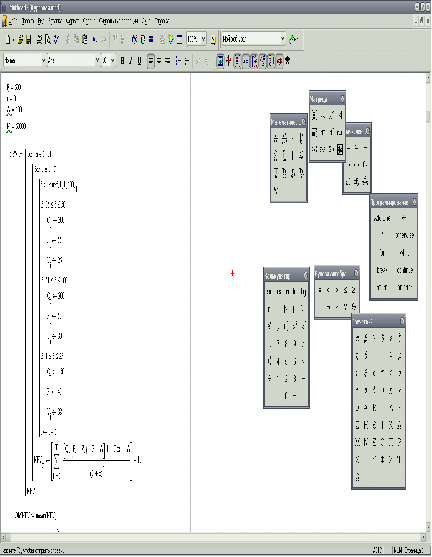
Итак, для выполнения данного задания требуется составить программу в MathCAD.

Для этого нужно составить схему. Далее мы создадим цикл длинной в 50000 ходов и рассчитаем 50000 различных значений NPV учитывая, что исходные данные Q P и V будут распределены случайным образом с распределением как в лекционном примере.

Чистая приведённая стоимость(NPV) будет подсчитана по формуле, которая дана в лекционном примере.

Далее мы считаем математическое ожидание полученного вектора NPV, его среднее квадратичное и коэффициент вариации. Используя эти данные, мы сможем подсчитать вероятность, что NPV < 0, двумя способами: по формуле MathCAD и с помощью цикла со счётчиком.

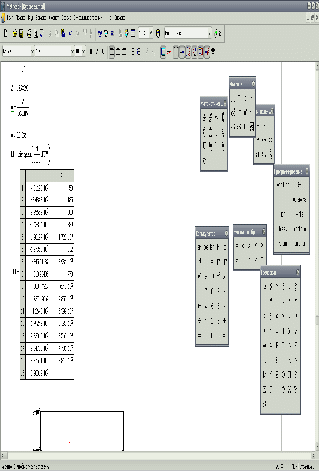
Таблица для заполнения матрицы будет выглядеть следующим образом:

Показатели

Наихудший

Наилучший

Вероятный

Q

150

300

200

P

40

55

50

V

38

25

30

Таким образом, начальные входные данные будут выглядеть следующим образом:

Дано в тексте лекционного задания:

Раздел 2. Блок-схема имитации

n=1

Генерация Q-вектора выборки Т объёмов выпуска ( в каждом из Т лет)

Генерация P-вектора выборки Т возможных цен ( в каждом из Т лет)

Генерация V-вектора выборки Т возможных переменных затрат (в каждом из Т лет)

Подсчёт NPV чистой приведённой стоимости проекта в n-ом прогоне

n = N

n:=n+1

Стоп. Готов вектор NPV – выборка из 50000 результатов имитации

Раздел 3. Программа и описание параметров

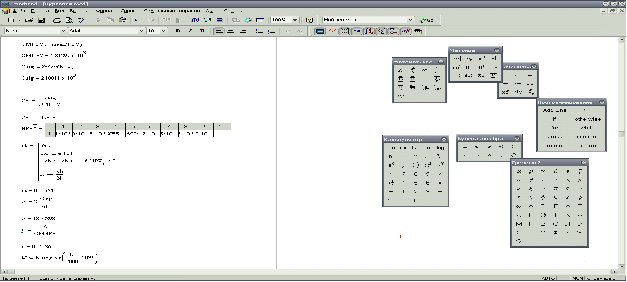
Исходные данные:

Цикл для создания вектора NPV:

Расчёт оценки математического ожидания и среднего квадратичного отклонения NPV:

Расчёт оценки коэффициента вариации и риска убытков с помощью функции pnorm:

Риск отрицательного NPV большой, можно посчитать его другим способом, с использованием цикла со счётчиком:

Расчёт ошибки при расчёте мат. ожидания NPV. Ошибка в рублях и в процентах:

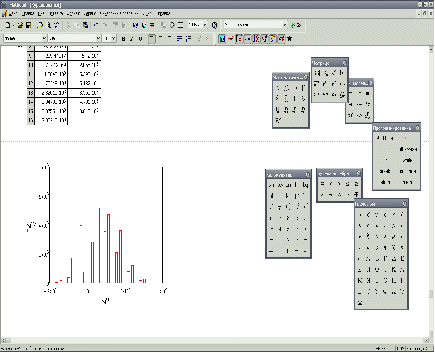
Для наглядности и удобства рассуждений выведем на экран гистограмму выборки NPV:

По гистограмме видно, что полученные значения рисков адекватны.

Заключение

Проведя анализ полученного вектора NPV, и сравнив результаты с лекционным примером можно сделать следующие выводы:

- Оценка мат. ожидания почти равны с лекционным примером;

- Коэффициент вариации больше 1,16>1, следовательно, можно говорить, что риск инвестиционного проекта выше среднего. В лекционном примере коэффициент вариации равен 0,784<1;

- Оценка риска убытков двумя способами подтвердила предыдущее умозаключение – вероятность убытков примерно 18%, что является большим значением риска. В лекционном примере значение риска убытков равно 10%;

- Оценка ошибки в расчётах равна 19, учитывая, что это 1% от математического ожидания, можно сказать, что это приемлемая погрешность и все расчёты можно считать адекватными.

Итак, проект является весьма рискованным, причём он является более рискованным, чем в лекционном примере. Все расчёты вполне адекватны, на что показывают допустимые значения ошибок.

Список используемых источников

1. Имитационное моделирование в экономике: учебное пособие/ С.М. Бородачев. — Екатеринбург: ГОУ ВПО «УГТУ–УПИ», 2007.— 35 с.