Оптимальное распределение неоднородных ресурсов
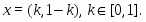
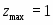
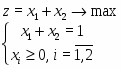
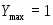
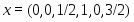
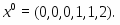
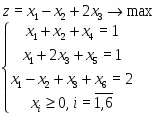
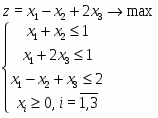
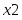
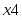
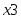
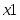
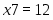
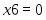
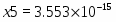
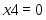
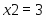
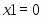
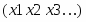
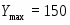
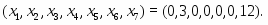
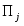
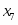
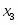
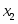
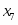
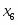
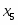
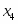
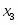
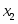
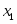
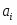
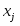
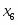
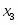
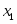
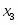
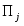
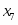
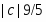
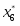
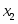
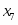
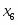
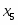
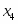
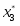
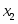
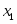
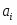
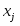
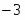
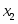
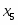
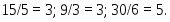
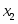
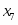
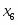
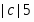
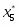
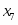
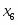
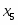
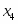
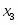
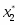
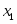
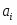
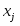
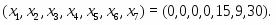
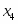
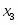
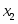
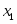
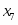
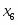
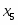
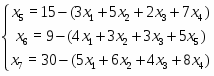
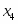
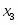
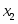
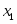
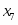
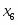
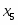
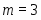
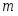
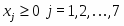
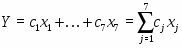
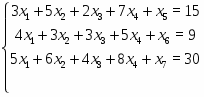
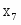
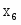
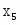
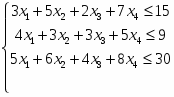
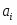
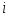
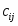
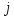
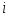
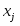
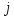
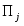
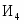
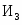
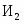
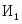
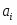
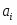
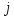
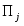
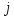
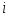
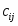
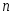
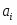
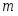
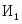
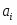
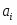
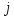
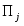
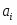
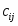
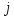
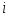
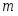
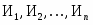
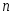 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
"Гомельский государственный университет имени Франциска Скорины"
математический факультет
кафедра ВМиП
Курсовая работа
"Оптимальное распределение неоднородных ресурсов"
Гомель 2006
Содержание
Введение 3
Постановка задач 5
Выявление основных особенностей, взаимосвязей и количественных закономерностей 6
Решение задачи традиционными методами 8
Решение задачи с использованием системы Mathcad 12
Заключение 18
Литература 19
В данной курсовой работе изложен метод решения задач об оптимальном распределении неоднородных ресурсов с помощью системы символьной математики Mathcad.
Как известно в настоящее время широко используются следующие системы символьной математики: Maple, Matlab, Mathematica, Reduce, Derive, Theorist, Macsyma. Почему же наш выбор пал на Mathcad? На это есть несколько причин:
1) Reduce, Derive, Theorist, Macsyma были созданы для совершенно других задач. Их основное назначение это доказательство теорем алгебры (Reduce, Macsyma). Derive, Theorist морально устарели еще 5 лет назад. Matlab ориентирован на работу с матрицами. Остаются только Maple, Mathematica и Mathcad.
2) Из этих программ только Mathematica и Mathcad обладают современными средствами визуализации представления данных. И запись в системе Mathcad наиболее приближена к записи математических задач без применения компьютера.
3) Mathcad изначально создавался для численного решения математических задач. С развитем Mathcad впитал в себя только лучшее от Maple (ядро для символьных вычислений) и Matlab (библиотеку высокоскоростных алгоритмов NAG).
4) Mathcad более доступен для массового пользователя.
В первом пункте курсовой приведены примеры типичных задач соответствующей тематики. Во втором пункте построена математическая модель данных задач. В третьем пункте приведен алгоритм симплекс-метода. Главное, что нам из него необходимо, это умение находить начальное приближение, остальное доделает Mathcad. В четвертом пункте приведен порядок действий для решения задач линейного программирования в системе Mathcad и приведены ряд примеров решения задач с использованием Mathcad. Так же приведены случаи, когда иследуемая целевая функция на заданном множестве ограничений не имеет экстремумов, или когда имеет более одного экстремума. В последнем случае предложена трактовка данного результата.
Постановка задач
В процессе производства постоянно возникают задачи определения оптимального плана производства продукции при наличии определенных ресурсов (сырья, полуфабрикатов, оборудования, финансов, рабочей силы и др.) или проблемы оптимизации распределения неоднородных ресурсов на производстве. Рассмотрим несколько возможных постановок таких задач.
Постановка задачи А. Для изготовления видов изделий необходимы ресурсы видов: трудовые, материальные, финансовые и др. Известно необходимое количество отдельного -го ресурса для изготовления каждого -го изделия. Назовем эту величину нормой расхода . Пусть определено количество каждого вида ресурса, которым предприятие располагает в данный момент, – . Известна прибыль , получаемая предприятием от изготовления каждого -го изделия. Требуется определить, какие изделия, и в каком количестве должно изготавливать предприятие, чтобы обеспечить получение максимальной прибыли. Необходимая исходная информация представлена в табл.
Данные для задачи A
Используемые ресурсы
Изготавливаемые изделия
Наличие ресурсов
Трудовые
3
5
2
7
15
Материальные
4
3
3
5
9
Финансовые
5
6
4
8
30
Прибыль
40
50
30
20
Постановка задачи В. Пусть в распоряжении завода железобетонных изделий (ЖБИ) имеется видов сырья (песок, щебень, цемент) в объемах , Требуется произвести продукцию видов. Дана технологическая норма . потребления отдельного -го вида сырья для изготовления единицы продукции каждого -го вида. Известна прибыль , получаемая от выпуска единицы продукции -го вида. Требуется определить, какую продукцию и в каком количестве должен производить завод ЖБИ, чтобы получить максимальную прибыль. Исходные данные представлены в табл.
Данные для задачи B
Используемые ресурсы
Изготавливаемые изделия
Наличие ресурсов
Песок
3
5
2
7
15
Щебень
4
3
3
5
9
Цемент
5
6
4
8
30
Прибыль
40
50
30
20
Постановка задачи С. Пусть на предприятии после модернизации производства появился свободный ресурс времени. Предлагается организовать производство новых изделий нескольких наименований. Известно время, требуемое на изготовление отдельного изделия на каждом оборудовании, свободные резервы времени на каждой машине, а также прибыль, получаемая от выпуска каждого изделия. Требуется определить, какие изделия, и в каком количестве целесообразно производить на предприятии, чтобы получить максимальную прибыль.
Выявление основных особенностей, взаимосвязей и количественных закономерностей
Количество изделий -го наименования, которое может производить предприятие, обозначим через . Зная количество каждого вида -го ресурса для изготовления отдельного -го типа изделия – норму расхода и количество каждого -го ресурса , можно записать следующую систему неравенств:
Полученную систему можно представить в виде совокупности равенств, если в каждое из неравенств ввести фиктивные изделия (дополнительные переменные) , , , при изготовлении которых используют каждый оставшийся вид ресурса.
В этом случае система равенств примет такой вид:
Это преобразование необходимо для упрощения вычислительной процедуры в дальнейшем. Прибыль, получаемая от фиктивных изделий, принимается равной нулю.
Построение математической модели. Критерий оптимизации (суммарную величину прибыли) можно тогда представить так:
Граничные условия будут записаны следующим образом:
Совокупность системы ограничений (2), целевой функции (3) и граничных условий (4) образует математическую модель для нашей задачи.
Решение задачи традиционными методами
Алгоритм решения. Для решения данной задачи разработано много способов. Рассмотрим один из наиболее распространенных – симплекс-метод. Для его использования необходимо определить начальный базис, то есть такое решение, которое удовлетворяет системе равенств (2). В некоторых задачах базис просматривается непосредственно, но во многих его необходимо найти.
В данной задаче базис определяется легко. Для этого требуется взять неизвестных по числу уравнений в системе (2), желательно наиболее редко встречающиеся в ней. В нашей совокупности уравнений () это , , , которые и выражаем через оставшиеся неизвестные , , , .
Систему уравнений необходимо записать в таком виде:
Переменные, находящиеся в левой части системы уравнений, называются базисными (основными), а находящиеся справа – небазисными (неосновными). Для определения значений базисных переменных , , необходимо приравнять к нулю небазисные , , , и подставить их в систему уравнений (5). Полученное таким образом решение называется базисным. В нашей задаче оно будет выглядеть следующим образом:
После определения начального базиса можно переходить непосредственно к использованию алгоритма симплекс-метода, который содержит следующие основные этапы:
1. Заполнение исходной симплекс-таблицы. В соответствии с полученной системой уравнений и критерием оптимизации заполняем исходную симплекс-таблицу.
Симплекс-таблица
Базисные переменные
Свободные члены
Коэффициенты при базисных и небазисных переменных
15
3
2
7
1
0
0
9
4
3
3
5
0
1
0
30
5
6
4
8
0
0
1
0
40
50
30
20
0
0
0
2. Проверка базисного решения на оптимальность. Просматриваются знаки коэффициентов при небазисных переменных в целевой функции (критерий оптимизации) – последняя строка табл.
Если все коэффициенты при небазисных переменных неположительны, то исходный базис является оптимальным; в противном случае переходят к следующему этапу. В нашей задаче решение не оптимально, так как все коэффициенты целевой функции при небазисных переменных положительны.
3. Проверка задачи на наличие решения. Если при какой-либо небазисной переменной, имеющей положительный коэффициент в целевой функции, окажется, что столбец коэффициентов при этой же переменной в системе уравнений состоит из одних неположительных чисел, то максимальное значение целевой функции стремится к бесконечности, то есть задача решений не имеет. В нашей задаче решение имеется.
4. Выбор из небазисных переменных той, которая способна при введении ее в базис увеличить значение целевой функции. Наиболее простой и чаще всего используемый способ состоит в выборе той небазисной переменной, которой соответствует наибольший положительный коэффициент в целевой функции. В нашей задаче это переменная (наибольший положительный коэффициент равен 50). Значит, необходимо ввести в базис.
5. Определение базисной переменной, которая должна быть выведена из базиса. Для всех положительных коэффициентов при вводимой в базис переменной в системе уравнений определяется отношение свободного члена уравнения к коэффициенту при вводимой в базис переменной. Для нашей задачи это будут следующие отношения:
Минимальное из полученных отношений указывает строку, базисную переменную, которая должна быть выведена из базиса. При наличии нескольких одинаковых отношений берется любое. В нашей задаче выведем из базиса переменную .
5. Представление новой базисной переменной через небазисные. Строится новая симплекс-таблица. Отмечается звездочкой строка и столбец в предыдущей симплекс-таблице, соответственно для выводимой из базиса и для вводимой в него переменной. Коэффициент, находящийся на пересечении строки и столбца, отмеченных звездочками, называется разрешающим и помечается звездочкой. Все коэффициенты строки, отмеченной звездочкой, делятся на разрешающий элемент, а результаты расчета заносятся в новую симплекс-таблицу. В нашей задаче на первой итерации разрешающий элемент равен 5. Результаты деления каждого элемента строки, отмеченной звездочкой, на разрешающий коэффициент заносятся в строку 1 новой таблицы.
6. Представление остальных базисных переменных и целевой функции через новый набор небазисных переменных. Для этого коэффициенты в новой таблице при новой базисной переменной умножаются на такое число, чтобы после сложения с преобразуемой строкой предыдущей таблицы в столбце при новой базисной переменной в новой таблице появился ноль. Результаты сложения заносятся в новую симплекс-таблицу. Исходя из этого, для получения коэффициентов второй строки в новой табл. умножаем коэффициенты при новой базисной переменной на число , складываем с соответствующими коэффициентами второй строки предыдущей симплекс-таблицы и результаты расчета заносим во вторую строку новой таблицы.
Вторая итерация симплекс-метода
Базисные переменные
Сбободные члены
Коэффициенты при базисных и небазисных переменных
3
3/5
1
2/5
7/5
1/5
0
0
0
11/5
0
4/5
-3/5
1
0
12
7/5
0
8/5
-2/5
-6/5
0
1
-150
10
0
10
-50
-10
0
0
Аналогичные преобразования проводим и для других строк. После этого выполняем новую итерацию. Цикл расчета начинается с этапа 2 и проводится до тех пор, пока не будет найдено оптимальное решение. Поскольку в последней строке табл. в целевой функции не все коэффициенты при небазисных переменных положительны, то решение не оптимально; следовательно, выполняется следующий итерационный цикл расчета и строится новая симплекс-таблица. В качестве вводимой в базис небазисной переменной берем (можно ) как имеющую наибольший положительный коэффициент. Отмечаем звездочкой столбец . В качестве выводимой из базиса переменной берем , так как для нее частное от деления свободного члена на соответствующий коэффициент минимально. Разрешающий множитель равен 9/5. Результаты расчета представлены в табл.
Третья итерация симплекс-метода
Базисные переменные
Свободные члены
Коэффициенты при базисных и небазисных переменных
3
1/9
1
0
1/9
1/3
-2/9
0
0
11/9
0
1
4/9
-3/9
5/9
0
12
-5/9
0
0
-10/9
-2/3
-8/9
1
-150
-20/9
0
0
-490/9
-20/3
-50/9
0
Последняя строка таблицы не содержит положительных коэффициентов при небазисных переменных. Анализируя полученное решение, видим, что оно оптимально и выглядит так:
Из полученного решения видно, что предприятию наиболее выгодно изготовление только изделия , производство которого обеспечит ему максимальную прибыль в размере . При этом материальные и трудовые ресурсы будут задействованы полностью, а финансовые – недоиспользованы на 12 единиц.
Решение задачи с использованием системы Mathcad
Введем сначала поясняющий текст в рабочем листе. Для этого разместим курсор (визир – красный крестик) в месте ввода текста. Затем выберем (щелчком мыши или с помощью клавиатуры) пункт Insert (Вставка) главного меню Mathcad. В появившемся падающем меню щелкнем по пункту Text Region (Текстовая область) или в месте расположения курсора нажмем клавишу с двойной кавычкой (команда для ввода текста). В обоих случаях появится шаблон, указывающий место и начало ввода текста, после чего можно приступить к этой операции. Текстовая область будет автоматически увеличиваться по мере ввода текста. По окончании этого действия выведем курсор за рамки текстовой области.
Далее введем критерий оптимизации – целевую функцию. Для этого разместим курсор (визир – красный крестик) в месте ввода математического выражения, затем, используя соответствующие клавиши, начнем ввод, в первую очередь – имени критерия оптимизации с аргументами в скобках через запятые. Затем нажмем комбинацию Shift+: (двоеточие) для ввода знака присваивания:= (двоеточие и знак ``равно''). На месте правой метки помещаем все выражение критерия оптимизации. Аналогично вводятся начальные приближения.
Для решения задачи используем блок функций Given…Maximize. Для этого необходимо:
• ввести, если требуется, комментарии, ввод которых начинается с нажатия клавиши с двойной кавычкой;
• ввести ключевое слово Given;
• ввести систему ограничений с использованием жирного знака равенства, нажав комбинацию клавиш Ctrl+=;
• ввести граничные значения;
• ввести вектор-столбец искомых параметров, используя диалоговое окно Insert Matrix (Вставить матрицу) и комбинацию Ctrl+M. В диалоговом окне число строк (Rows) – элементов вектора столбца – должно быть равно 7, а число столбцов (Columns) – 1;
• ввести знак присваивания, нажав комбинацию клавиш Shift+: (двоеточие);
• ввести функцию Maximize с искомыми параметрами, используя диалоговое окно Insert Function (Вставить функцию) и комбинацию Ctrl+E;
• ввести вектор-столбец искомых параметров и знак ``равно''.
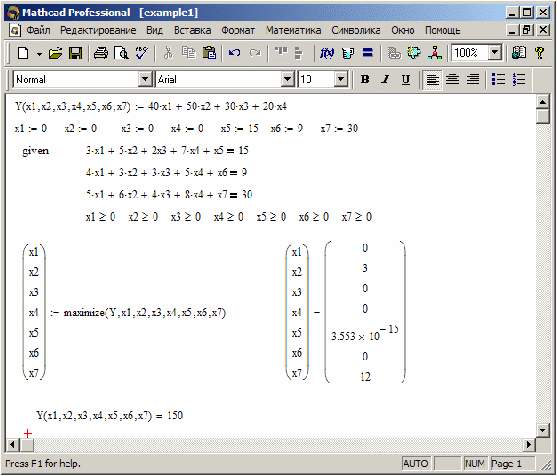
На рис. 1 показан процесс оптимизации распределения неоднородных ресурсов с помощью Mathcad.
Решение задачи А с помощью Mathcad
Оптимальное распределение неоднородных ресурсов зафиксировано в векторе . Из полученного решения видно, что , , , , , . Это означает, что изделия , и предприятие изготавливать не должно. Ему нужно производить только второе изделие в количестве 3 единиц. Цифра в переменной определяет изделие, планируемое для изготовления. Оптимальное распределение ресурсов обеспечит получение максимальной прибыли , которая составит 150 единиц.
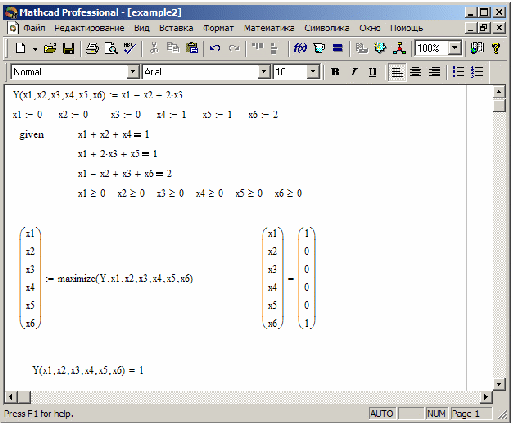
В качестве еще одного примера решим в системе Mathcad следующую задачу линейного программирования:
Приведем ее к каноническому виду:
Очевидно, что в качестве начального приблежения необходимо взять Решение задачи приведено на рисунке 2.
Решение задачи (6) с помощью Mathcad pic2
Задача о нахождении минимума целевой функции, в системе символьной алгебры Mathcad, решается так же просто. Для этого достаточно заменить функцию maximize на minimize.
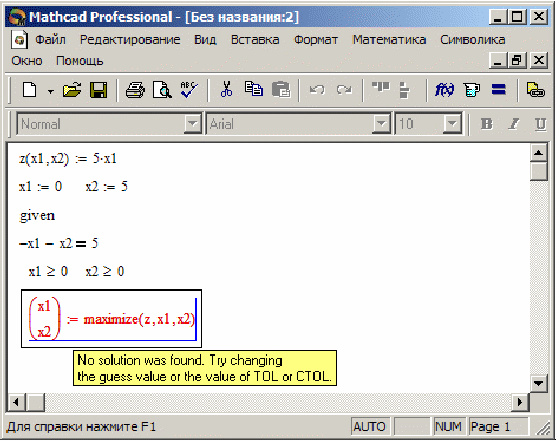
Как показывает практика Mathcad корректно решает задачи в которых функция не достгает максимума (минимума) на ограниченном множестве. В этом случае Mathcad выводит соответствующее сообщение (см. рис. 3).
Решение задачи не имеющей максимума pic3
К сожалению Mathcad некорректно решает задачи в которых оптимальное решение неединственно. В этом случае решением служит одна из точек в которых достигается максимум (минимум). Так например при решении задачи (6) симплекс-методом, то получим, что . В обоих случаях . Лучше всего это прослеживается при решении следующей задачи:
Очевидно, что , а
Задавая начальные приближения в соответствии с формулой приведенной выше, Mathcad будет выдавать в качестве ответа начальные приближения.
В случае задачи (7) нам действительно безразлично в каком количестве выпускать товары 1 и 2, прибыль от этого не меняется. Но если мы откажемся от выпуска одного из товаров, мы повысим прибыль за счет снижения затрат на обслуживание одного из станков, мы можем его вообще продать, сдать в аренду, сократить рабочих, обслуживающих данный станок. Решение в таком случае должен принимать управляющий.
Заключение
Как было показано выше система символьной математики идеально подходит для решения задач исследования операций и в частности задач оптимального распределения неоднородных ресурсов. Mathcad в считаные секунды находит решение подобных задач, даже в случае порядка ста или двухсот переменных.
Приведенным алгоритмом можно пользоваться и в случае, если задача представляет собой задачу выпуклого программирования с нелинейными ограничениями и с нелинейной целевой функцией.
Mathcad не требует от пользователя знание каких-то определенных методов решения поставленных задач, пользователь должен только уметь составить математическую модель, а все остальное сделает Mathcad. Но поскольку Mathcad – это всего лишь программа пользователь должен понимать, что при решении может возникнуть ошибки, могут быть получены далеко не все решения и, самое главное, Mathcad не интерпретирует полученные результаты, а только решает.
1. Венцель Е.С., Исследование операций, – М., 1980
2. Давыдов Э.Г., Исследование операций, – М., 1990
3. Вагнер Г., Основы исследования операций в 2-х т.
4. Кудрявцев Е.М., Mathcad 8, – М.: ДМК, 2000
5. Гермейер Ю.Б., Введение в теорию ИСО

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ