Построение графиков функций
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра автоматизации производственных процессов
Тема курсовой работы:
«Построение графиков функций»
Курсовая работа
Расчетно-пояснительная записка.
Дисциплина: Программирование и основы алгоритмизации
Студент: Яковлев П. С.
Группа: Т-2144
Руководитель: Скобелев И. В.
Комиссия__________________
Оценка____________________
Дата защиты_______________
Курган, 2006г.Оглавление
Техническое задание
Общая блок-схема алгоритма
Описание работы программного продукта
Инструкция по инсталляции программного продукта
Инструкция оператору
Ограничения данной версии программы
Вывод
Список используемой литературы
1. Техническое задание
Программный продукт GRAPHIC позволяет строить и сохранять графики любых функций одной переменной. Продукт разработан на языке программирования Мicrosoft Visual C++ 6.0 с использованием объектно-ориентированной методологии. Диалог пользователя с программой, а именно введение параметров, осуществляется посредством диалоговых окон программы. Диапазон вводимых значений программно ограничен, с целью недопущения некорректной работы или возникновения ошибки.
2. Общая блок-схема алгоритма
Общая блок схема алгоритма программы GRAPHIC:
Вывод изображения
на экран
Ввод функции, значений начала и конца отрезка
Вычисление координат точек графика, формирование изображения
3. Описание работы программного продукта
Программа “GRAPHIC” позволяет строить и сохранять графики функций одной переменной. При открытии программы появляется окно, в котором уже по умолчанию построен график функции f(x)=sin(x)+0.05*x на отрезке [-5,10]. Выбрав на панели меню пункт Функция, и, изменяя поле ввода в появившемся диалоговом окне, можно построить необходимый график функции или изменить отрезок, на котором построен график.
Для того, чтобы лучше понять работу программы приведем некоторые коды
class CGRAPHICView : public CView //Класс Single Document
{
public:
CString sFunc;
double XX;
double X1;
double X2;
int SdvX;
int SdvY;
int DlX;
int DlY;
CDC* pDCbuf;
bool GbNeedRepaint;
CMFunc vFunc;
CFuncEval FuncEval;
void Vichislenie();
void VFillBuffer (CDC* pSrcDC);
//Остальные свойства и методы класса Single Document
};
class CMFunc //Класс расчета функции
{
public:
double FXX[400];
double FYY[400];
bool FYYER[400];
int KolT;
double MinY;
double MaxY;
void FuncMaxMinY();
CMFunc();
};
void CGRAPHICView::OnDraw(CDC* pDC) //Функция прорисовки документа
{
CGRAPHICDoc* pDoc = GetDocument();
ASSERT_VALID(pDoc);
// TODO: add draw code for native data here
try
{
VFillBuffer(pDC);
}
catch (...)
{
MessageBox(_T("Ошибка построения графика!"),_T("Ошибка"));
}
}
void CGRAPHICView::Vichislenie() //Функция вычисления параметров функции
{
int a; double shag;
extern BOOL bMathError;
FuncEval.SetString(sFunc);
//Вычисляем шаг shag
shag=((X2-X1)/(vFunc.KolT-1));
//Вычисляем узлы функции vFunc.FXX[a]
for(a=0;a<(vFunc.KolT-1);a++)
vFunc.FXX[a]=X1+a*shag;
vFunc.FXX[vFunc.KolT-1]=X2;
//Вычисляем значения функции в узлах vFunc.FYY[a] и ошибку вычисления vFunc.FYYER[a]
for(a=0;a
bMathError = FALSE;
XX=vFunc.FXX[a];
vFunc.FYY[a] = FuncEval.Compute ();
vFunc.FYYER[a] = bMathError;
}
//Вычисляем max и min значения функции vFunc.MaxY и vFunc.MinY
vFunc.FuncMaxMinY();
}
void CGRAPHICView::VFillBuffer (CDC* pSrcDC) //Функция рисования графика
{
int OtstX;
int OtstY;
int DlOX;
int DlOY;
int KolLX;
int KolLY;
SdvX=30;
SdvY=30;
DlX=700;
DlY=370;
OtstX=80;
OtstY=30;
DlOX=DlX-OtstX-50;
DlOY=DlY-2*OtstY;
KolLX=10;
KolLY=10;
double KoefX;
double KoefY;
int a; double d,dd; CString sss;
if(GbNeedRepaint==TRUE) {
//Вычисление параметров функции (объект vFunc класса CMFunc)
Vichislenie();
//???????????????????????????????????????????????
pDCbuf->DeleteDC ();
pDCbuf->CreateCompatibleDC (pSrcDC);
CBitmap bitmap;
bitmap.CreateCompatibleBitmap(pSrcDC,DlX,DlY);
CBitmap* pbmp=pDCbuf->SelectObject(&bitmap);
//Рисование графика-------------------------------------------------
//Цвета (разметки (линий) - cvet1, осей - cvet2, графика - cvet3)
CPen cvet1(PS_SOLID,1,RGB(100,100,50));
CPen cvet2(PS_SOLID,1,RGB(200,0,200));
CPen cvet3(PS_SOLID,1,RGB(255,0,0));
//Отключаем фон текста и устанавливаем цвет текста
pDCbuf->SetBkMode(TRANSPARENT);
pDCbuf->SetTextColor(RGB(0,0,210));
//Закрашиваем область графика
pDCbuf->FillSolidRect(0,0,DlX,DlY,RGB(235,235,235));
//Рисование разметки X
pDCbuf->SelectObject(cvet1);
d=((double)DlOX/(KolLX-1));
for(a=0;a
pDCbuf->MoveTo(OtstX+(int)(a*d),OtstY);
pDCbuf->LineTo(OtstX+(int)(a*d),OtstY+DlOY);
}
//Рисование разметки Y
d=((double)DlOY/(KolLY-1));
for(a=0;a
pDCbuf->MoveTo(OtstX,OtstY+(int)(a*d));
pDCbuf->LineTo(OtstX+DlOX,OtstY+(int)(a*d));
}
//Подписи X
d=(X2-X1)/(KolLX-1);
dd=((double)DlOX/(KolLX-1));
for(a=0;a<(KolLX-1);a++) {
sss.Format(_T("%.3f"),X1+a*d);
pDCbuf->TextOut(OtstX+(int)(a*dd)-4*sss.GetLength(),OtstY+DlOY+3,sss);
}
sss.Format(_T("%.3f"),X2); a=KolLX-1;
pDCbuf->TextOut(OtstX+(int)(a*dd)-4*sss.GetLength(),OtstY+DlOY+3,sss);
//Подписи Y
d=(vFunc.MaxY-vFunc.MinY)/(KolLY-1);
dd=((double)DlOY/(KolLY-1));
for(a=1;a<(KolLY-1);a++) {
sss.Format(_T("%.3f"),vFunc.MinY+a*d);
pDCbuf->TextOut(OtstX-3-7*sss.GetLength(),OtstY+DlOY-(int)(a*dd)-7,sss);
}
sss.Format(_T("%.3f"),vFunc.MinY);
pDCbuf->TextOut(OtstX-3-7*sss.GetLength(),OtstY+DlOY-12,sss);
sss.Format(_T("%.3f"),vFunc.MaxY); a=KolLY-1;
pDCbuf->TextOut(OtstX-3-7*sss.GetLength(),OtstY+DlOY-(int)(a*dd)-7,sss);
//Подпись "График функции..."
sss.Format(_T(" на отрезке [%.2f,%.2f]"),X1,X2);
pDCbuf->TextOut(OtstX+80-2*sFunc.GetLength(),OtstY-25,(_T("График функции f(x)=")+sFunc+sss));
//Вычисления коэффициентов сжатия на экране KoefX и KoefY
KoefX=((double)DlOX)/(X2-X1);
KoefY=((double)DlOY)/(vFunc.MaxY-vFunc.MinY);
//Рисование осей X и Y
pDCbuf->SelectObject(cvet2);
if(X1<=0&&X2>=0) {
pDCbuf->MoveTo(OtstX-(int)(X1*KoefX),OtstY);
pDCbuf->LineTo(OtstX-(int)(X1*KoefX),OtstY+DlOY);
}
if(vFunc.MinY<=0&&vFunc.MaxY>=0) {
pDCbuf->MoveTo(OtstX,OtstY+DlOY+(int)(KoefY*vFunc.MinY));
pDCbuf->LineTo(OtstX+DlOX,OtstY+DlOY+(int)(KoefY*vFunc.MinY));
}
//Рисование самого графика функции
pDCbuf->SelectObject(cvet3);
for(a=1;a
if(vFunc.FYYER[a-1]==FALSE&&vFunc.FYYER[a]==FALSE) {
pDCbuf->MoveTo(OtstX+(int)(KoefX*(vFunc.FXX[a-1]-X1)),OtstY+DlOY-(int)(KoefY*(vFunc.FYY[a-1]-vFunc.MinY)));
pDCbuf->LineTo(OtstX+(int)(KoefX*(vFunc.FXX[a]-X1)),OtstY+DlOY-(int)(KoefY*(vFunc.FYY[a]-vFunc.MinY)));
}
}
//------------------------------------------------------------------
GbNeedRepaint=FALSE;
}
//Копирование буфера pDCbuf на экран
pSrcDC->BitBlt (SdvX, SdvY, DlX, DlY, pDCbuf, 0, 0, SRCCOPY);
}
void CGRAPHICView::OnFileSave() //Функция сохранения графика
{
HRESULT hResult;
CString strFilter;
strFilter = "PNG image (*.png)|*.png||";
CFileDialog dlg(FALSE,_T("png"),NULL,OFN_HIDEREADONLY | OFN_OVERWRITEPROMPT | OFN_EXPLORER,strFilter);
hResult = (int)dlg.DoModal();
if (hResult != IDOK) {MessageBox("Отменено пользователем","Предупреждение"); return;}
CString strFileName;
strFileName = dlg.m_ofn.lpstrFile;
CImage imgOriginal;
imgOriginal.Create (DlX, DlY, 24);
//Это позволяет нарисовать все что должно быть сохранено
(pDCbuf->FromHandle (imgOriginal.GetDC ()))->BitBlt (0, 0, DlX, DlY, pDCbuf, 0, 0, SRCCOPY);
hResult = imgOriginal.Save(strFileName);
try
{
imgOriginal.ReleaseDC ();
imgOriginal.Detach ();
imgOriginal.Destroy ();
}
catch (...)
{
}
if (FAILED(hResult)) {
MessageBox("Ошибка сохранения!","Ошибка!");
}
}
4. Инструкция по инсталляции программного продукта
Для установки программы запустите файл GRAPHICv1.0\setup.exe и следуйте инструкциям мастера. Для удаления программы можно воспользоваться этим же файлом.
Гарантируется работа данной программы в операционной системе Windows не ниже 98. В предыдущих версиях работа программы не проверялась.
Установка программы требует около 1 Мб свободной памяти на жестком диске.
Внимание!
За возможные ошибки, сбои, возможный причиненный моральный или материальный ущерб и т.д., авторы ответственности не несут. Вы используете программу на свой страх и риск!
Если вы не согласны с этим, то не используйте данную программу!
5. Инструкция оператору
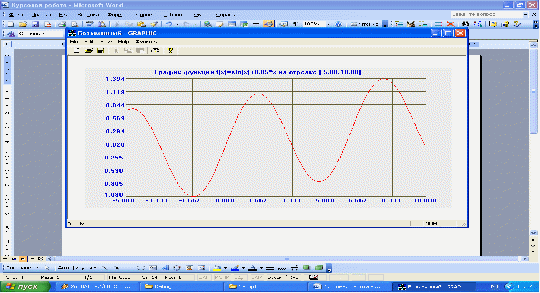
При открытии программы появляется окно, в котором уже по умолчанию построен график функции f(x)=sin(x)+0.05*x на отрезке [-5,10], как показано на рисунке:
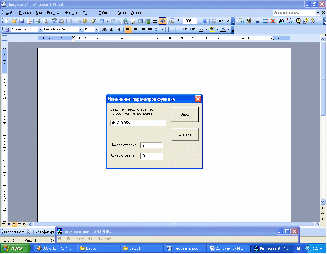
Чтобы построить необходимый график функции или изменить отрезок, на котором построен график, выберите на панели меню пункт Функция. При этом появится такое диалоговое окно:
В этом окне вы можете изменять параметры функции. Начало и конец отрезка могут быть введены любые из отрезка [-1.7976931348623158e+308, 1.7976931348623158e+308], но при этом начало должно быть меньше конца отрезка, иначе появится сообщение об ошибке.
С функцией дело немного сложнее. Чтобы интерпретатор правильно понял функцию, при её вводе нужно пользоваться правилами.
Унарные операции:
cos(x) - косинус
sin(x) - синус
tg(x) = tan(x) - тангенс
ctg(x) - котангенс
arccos(x) = acos(x) - арккосинус
arcsin(x) = asin(x) - арксинус
arctg(x) = atan(x) - арктангенс
arcctg(x) - арккотангенс
round(x) - обычное округление до целого
sqr(x) - квадрат
sqrt(x) - арифметический корень
abs(x) = fabs(x) - модуль
neg(x) - отрицание
fact(x) - факториал
exp(x) - экспонента
ln(x) - натуральный логарифм
log10(x) = lg(x) - десятичный логарифм
cosh(x) - гиперболический косинус
sinh(x) - гиперболический синус
tanh(x) - гиперболический тангенс
floor(x) - округление с недостатком
ceil(x) - округление с избытком
sign(x) - знак числа
inv(x) - логическая инверсия
- - отрицание
Бинарные операции:
(по приоритету с наименьшего)
x+y = add (x, y) - сложение x с y
x-y = sub (x, y) - вычитание из x y
x*y = mul (x, y) - умножение x на y
x/y = div (x, y) - деление x на y
x&y = log (x, y) - логарифм от x по основанию y
x^y = pow (x, y) - возведение x в степень y
x=y = x==y = equal (x, y) - если x = y, то 1 иначе 0
x
x>y = greater (x, y) - если x > y, то 1 иначе 0
and (x, y) - логическое И
or (x, y) - логическое ИЛИ
xor (x, y) - логическое сложение по модулю 2 (операция, исключающая ИЛИ) - сумма Жегалкина
pirs (x, y) - стрелка Пирса
shef (x, y) - штих Шеффера
impl (x, y) - логическая импликация
eq (x, y) - логическая эквиваленция
less (x, y) - x
greater (x, y) - x>y?
less_or_equal (x, y) - x<=y?
greater_or_equal (x, y) - x>=y?
max (x, y) - большее из x и y
min (x, y) - меньшее из x и y
equal (x, y) - эквиваленция
percent (x, y) - процент y от x
rand (x, y) - случайное число от x до y
Для всех логических операций число отличное от 0 это 1 (ПРАВДА), иначе 0 (ЛОЖЬ).
Числа пишутся в диапазоне [-1.7976931348623158e+308, 1.7976931348623158e+308]. Числа всегда записываются в десятичной форме, например 1 1f 1.0 1,0 1.0f 1,0f - одно и то же число в шести разных формах. Нельзя записывать числа в экспонентной форме, например 2.3e-5, вместо этого 2.3*(10^-5). Можно использовать константы: pi – число π, e – число e. Переменной является буква x. Между функциями можно ставить разделитель – пробел(space).
Чтобы сохранить изображение выберите во вкладке Файл -> Сохранить или Сохранить как. При этом появится стандартное диалоговое окно сохранения, где выбирается путь для сохранения. Изображения сохраняются в формате png.
6. Ограничения данной версии программы
Гарантируется работа данной программы в операционной системе Windows не ниже 98. В предыдущих версиях работа программы не проверялась.
При работе с программой нужно пользоваться правилами, которые приведены в разделе Описание работы программного продукта. В этом случае гарантируется правильная работа программы. Причем нужно обязательно соблюдать правила ввода функции, интерпретатор в этом случае поймет функцию правильно. Если в поле ввода функции ввести что-то неоговоренное правилами, интерпретатор примет это значение в любом случае, и не будет выведено никакого сообщения. Интерпретатор поймет, то что сможет распознать, остальное он игнорирует. Например, если будет введено “zxczxc” или пустая строка, то функция воспримется, как f(x)=0. Если будет введено “dghld+sin(x)asdfasf+dfgdfg”, то функция воспримется, как f(x)=sin(x).
7. Вывод
Написанная мною программа, позволяет решать важнейшую задачу математического анализа – построение графиков функций. Она может облегчить работу исследования функций. Программный продукт GRAPHIC может быть использован для учебных целей.
Программа написана при использовании самых современных на сегодняшний день технологий программирования и обеспечивает быструю и качественную работу.
Список используемой литературы
Язык программирования Си++. Курс лекций. Учебное пособие / Издание второе, исправленное / Фридман А. Л. / М.: «Интернет-университет Информационных Технологий», 2004.– 264 с.
Язык Си++. Учебное пособие / Издание пятое / Подбельский В. В. / М.: Финансы и статистика, 2001.– 560 с.: ил.
http: //www.holzner.ru.
http: //www.firstsleps.ru.
http: //www.intuit.ru.

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ