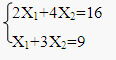
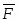
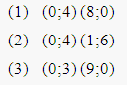
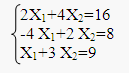
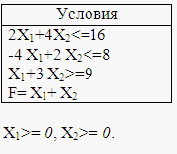
Задание 1. Вычисление регрессионных зависимостей

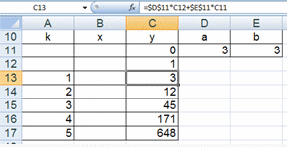
1.1. Вычислить значения регрессионно - авторегрессионой зависимости Y_k = Y_k-1 + a * X_k + b для k = 1, 2, 3, 4, 5, если X_k = k , Y₀ = 0, a = 3 b=3.

Рисунок 1.1 Исходные данные и результат вычислений к п.1.1

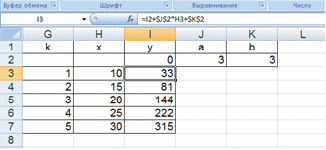
1.2. Вычислить значения регрессионно-авторегрессионой зависимости Y_k = Y_k-1 + a * X_k + b для k = 1, 2, 3, 4, 5, если a =3 b=3, Y₀ = 0, а {X_k} = {10, 15, 20, 25, 30}.

Рисунок 1.2 Исходные данные и результат вычислений к 1.2

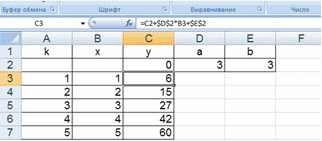
1.3. Вычислить значения авторегрессионой зависимости второго порядка Y_k = a*Y_k-1 + b * Y_k-2 для k = 1, 2, 3, 4, 5, если a =3 b=3, Y₀ =1, а Y_-1 =0.

Рисунок 1.3 Исходные данные и результат вычислений к п. 1.3

Задание 2. Применение идентификации регрессионных зависимостей

Предприятие производит выпуск продукции, количество которой Q зависит от управления (привлеченных средств) С. Различные варианты эмпирической зависимости Q = Q(С) даны в таблице. Варианты эмпирической зависимости соответствует номеру столбца таблицы, содержащего данные Q.

Условие

С

Q₀

1

2

2

1

3

3

4

3

5

4

6

6

7

6

8

5

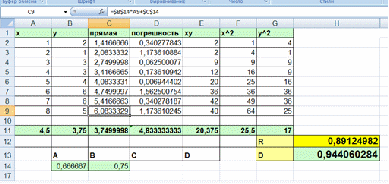
2.1. Задайте вид математической модели зависимости Q = Q(С) в виде линейного уравнения регрессии.

Рисунок 2.1 Исходные данные с вычислением полученных данных.

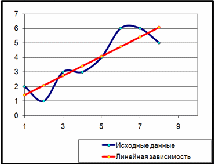
Рисунок 2.2 График построения исходной и линейной зависимости

2.2. Определите его адекватность эмпирическим данным, используя критерии качества модели:

1. коэффициент корреляции COR;

2. D - коэффициент детерминации;

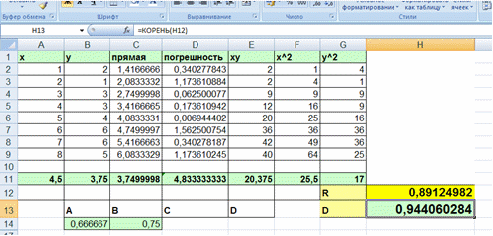
Рисунок 2.3 Нахождение коэффициента корреляции COR

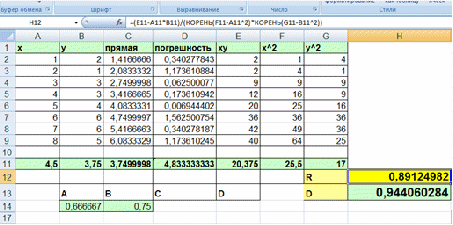
Рисунок 2.4 определение коэффициента детерминации D

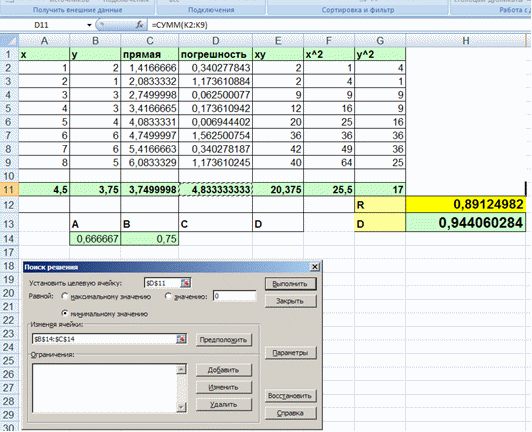
2.3. Подготовьте данные для расчетов средствами Excel, оформив соответствующий шаблон решения задачи.

Рисунок 2.5 Определение данных с помощью средства Excel "Поиск решения"

Задание 3. Оптимизация производственных и коммерческих операций

регрессионный линейный программирование математический

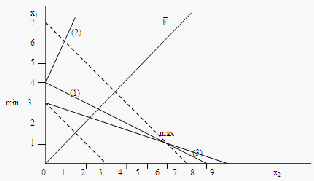
3.1. Найти графическое решение задачи линейного программирования (найти max и min целевой функции).

Преобразуем систему неравенств в систему уравнений.

Найдем производную F по X₁ и X₂ F¹ (1;1)

Найдем по две точки каждой прямой и проведем через них линии:

Рисунок 3.1 Графическое решение задачи линейного программирования

Определим область поиска решений.

После этого построим вектор , проведем через него перпендикуляр. При опускании его к центру координат определим точки max и min.

Из графика видно, что точка max образуется при пересечении прямых (1) и (3). Найдем ее координаты:

В результате получим X₁ = 6; X₂ = 1. Значение целевой функции будет равным F_max = 1*6+1*1 = 7

Как видно из графика точка min X₁ = 0; X₂ = 3. Значение целевой функции будет равным F_min = 1*0+1*3 = 3

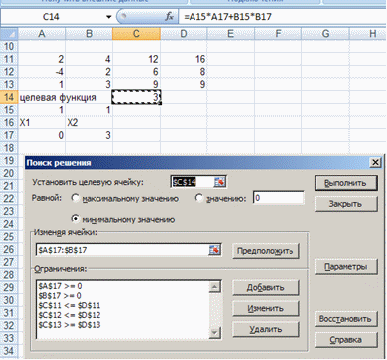
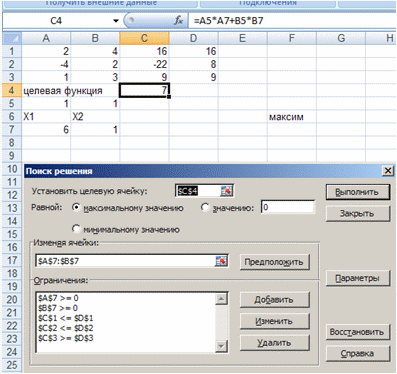
3.2. Подготовить шаблон для решения задачи средствами Excel и отобразить необходимые команды в интерфейсе инструмента "Поиск решения".

Определим max и min целевой функции, для этого заполним в Excel таблицу с данными ограничениями. С помощью средства Excel "Поиск решения" выполним данное задание:

Рисунок 3.2 Определение max целевой функции

Рисунок 3.3 Определение min целевой функции