Внеклассное мероприятие "Практическое применение системы программирования Visual Basic"
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 14» имени А.М.Мамонова
г. Старый Оскол Белгородской области
Внеклассное мероприятие по теме:
«Практическое применение системы программирования
Visual Basic»
Подготовила Соколатова Лилия Ивановна,
учитель информатики
Старый Оскол
2014
ПЛАН УРОКА
Тема мероприятия: «Практическое применение системы программирования Visual Basic».
Цели и задачи:
развитие познавательного интереса учащихся,
повышение интереса к программированию,
выявление межпредметных связей,
развитие логического мышления,
получение навыка работы в команде.
Оборудование:
видеопроектор,
персональный компьютер,
раздаточный материал.
ХОД УРОКА
1). Организационный момент (1минута).
2). Основная часть (40 минут).
Учитель:
Тема нашего занятия: «Практическое применение системы программирования Visual Basic».
На первый взгляд может показаться, что информатика – это сухой и скучный предмет, в котором царят цифры, объекты, блок-схемы, операторы. Однако сегодня мы увидим, что программирование – это увлекательное занятие, которое помогает изучать математические функции, моделировать физические явления, создавать дизайнерские проекты.
Давайте представим, что мы находимся не просто в кабинете информатики. Мы – в научно-исследовательской лаборатории, где трудятся две команды «Почемучки» и «Буквоежки». Каждая из команд работала над определенной темой, и результатом этой работы стали два интересных проекта.
Команда «Почемучки»
Команда «Буквоежки»
Тема проекта
Программирование повторений с помощью цикла со счётчиком
Программирование повторений с помощью цикла с условием
Цели и задачи проекта
применение знаний по предмету «Информатика» для решения задач с использованием персонального компьютера,
моделирование поведения функций и объектов при изменении условий, аргументов, параметров,
моделирования физических явлений и процессов,
определение межпредметных связей.
Первой свою работу представляет команда «Почемучки».
Капитан команды «Почемучки»:
Наша команда «Почемучки» работала над проектом «Программирование повторений с помощью цикла со счётчиком». В рамках этого проекта мы представляем решение четырех задач:
1. Демонстрация метода Line.
2. Построение графика функции y = a * x ^ 2 + b * x + c.
3. Построение графика функций y = sin ( x ), y = cos ( x ).
4. Графическая форма.
1-ый участник команды «Почемучки»:
Персональный компьютер способен выполнять огромное (по человеческим понятиям) число операций за короткое время, поэтому совершаемые им повторения приводят к потрясающим результатам.
Повторение – это многократное выполнение одного или нескольких предписаний алгоритма.
В языке программирования Visual Basic используется так называемый цикл со счётчиком. Для этого применяют оператор цикла For … Next.
2-ой участник команды «Почемучки»:
Логика работы оператора цикла со счётчиком такая. Прежде всего, цикл проверяют на непротиворечивость. Это означает, что если конечное значение счётчика больше начального, то шаг цикла должен быть положительным, а если конечное значение меньше начального, то шаг должен быть отрицательным.
Если проверка выявила указанное противоречие, работа цикла будет немедленно прекращена. У счётчика остается его начальное значение, и будут выполняться операторы, следующие за оператором цикла.
А если противоречия нет, то повторяющиеся операторы будут выполняться при начальном значении счётчика. Затем значение счётчика будет изменено на величину шага цикла.
3-ий участник команды «Почемучки»:
Предлагаем вашему вниманию решение задачи 1.1.
Проект № 1. Циклы со счетчиком
Задача 1.1. Демонстрация метода Line
Private Sub
Scale ( -300, 300 ) – ( 300, -300 )
For i % = 0 To 255
Line ( -255 + i, 255 – i ) – ( 255 – i, -255 + i ), RGB ( i, i, i ), BF
Next i
End Sub
Здесь применяется цикл со счетчиком, и число повторений составляет 255.
Запускаем программу.
Мы видим изображение цветного прямоугольника.
Для достижения различных вариаций цветовой гаммы, необходимо в функции RGB изменить индексные показатели – RGB (i, i, 0), RGB (i, 0, i), RGB (0, 200, i).
Возвращаемся к первоначальному изображению – RGB (i,i,i).
Капитан команды «Почемучки»:
Изменяя размеры фигуры, создавая цветовые вариации, можно добиться различных интересных эффектов. Практическое применение данной задачи – использование в дизайнерских проектах.
Вопрос: Можно ли добиться еще каких либо эффектов кроме изменения цветовой гаммы?
Ответ: Да, можно. Например, сделать прямоугольники без заливки. Для этого в операторе Line необходимо BF заменить на B.
4-ый участник команды «Почемучки»:
Циклы со счётчиком удобно применять для построения графиков функций. График функции строится на отрезке оси абсцисс «по точкам», когда для каждого значения аргумента Х на этом отрезке компьютер может легко найти значение Y этой функции и поместить на плоскость чертежа точку с координатами (x,y). Точек может быть очень много – при этом для глаза они будут сливаться в сплошную линию – график функции.
Представляем решение задачи 1.2.
Проект № 1. Циклы со счетчиком
Задача 1.2. Построение графика функции y = a * x ^ 2 + b * x + c ,
где a = 1, b = -2, c = -3
Private Sub
Picture1. Scale ( -6, 5 ) – ( 7, -5 )
Picture1. Line ( -6, 0 ) – ( 7, 0 ), vbCyan
Picture1.DrawWidth = 5
For i = -6 To 7
Picture1. PSet ( i, 0 ), vbRed
Picture1. Print i
Next i
Picture1. Line ( 0, -5 ) – ( 0, 5 ), vbCyan
For i = -4 To 5
Picture1. PSet ( 0, i ), vbRed
Picture1. Print i
Next i
For x = -6 To 7 Step 0.01
Y = x ^ 2 – 2 * x – 3
Picture1. PSet ( x, y), vbYellow
Next x
End Sub
Изменяя некоторые параметры, можно проследить изменение поведения функции. Например, изначально функция пересекает ось Y в точке (0, -3). Если с = 1, то функция будет пересекать ось Y в точке (0, 1). Ветви параболы направлены вверх. При a = -1 ветви параболы опускаются вниз.
Таким образом решение данной задачи позволяет детально изучить поведение функции
y = a * x ^ 2 + b * x + c при изменении различных ее параметров.
Вопрос: Изображение параболы строится благодаря оператору PSet и состоит из множества точек. Почему мы видим не разрозненные точки, а сплошную линию?
Ответ: Эффект сплошной линии создается благодаря очень маленькому шагу – в нашем примере 0,01. Если величину шага увеличить (например до 0,1 или 0,5) то эффект сплошной линии пропадёт.
5-ый участник команды «Почемучки»:
Цель работы над задачей 1.3. – построение графиков тригонометрических функций. Представляем решение задачи.
Проект № 1. Циклы со счетчиком
Задача 1.3. Построение тригонометрических функций
( y = sin ( x ), y = cos ( x ))
Private Sub
Picture1. Scale ( -10, 6 ) – ( 10, -6 )
For i % = -10 To 10
Picture1.Line ( i, -6 ) – ( i, 6 ), vbYellow
Next i
For k ! = -6 To 6
Picture1.Line ( -10, k ) – ( 10, k ), vbYellow
Next k
Picture1. Line ( -10, 0 ) – ( 10, 0 )
Picture1. Line ( 0, -6 ) – ( 0, 6 )
Picture1.DrawWidth = 3
For m = -6 To 6
Picture1.PSet (0, m), vbRed
Picture1.Print m
Next m
d ! = 0.01
For x ! = -10 To 10 Step d
Picture1. PSet ( x, Sin (x)), vbRed
Next x
End Sub
График функции y = sin ( x ) представлен зелёным цветом, а y = cos ( x ) - красным.
Давайте понаблюдаем как изменится поведение функции y = cos ( x ) при изменении аргумента на ( 2*х ), на ( ½ *х ).
К смещению функции y = sin ( x ) приведет изменение аргумента ( х ) на ( х + 8 ).
Таким образом, решение задачи позволяет моделировать поведение тригонометрических функций.
Капитан команды «Почемучки»:
При рассмотрении задач 1.2. и 1.3. прослеживается связь между учебными дисциплинами -информатика тема: «Программирование повторений с помощью цикла со счётчиком» и алгебра тема: «Графики функций».
6-ой участник команды «Почемучки»:
Представляем программу 1.4. Графические формы.
Проект № 1. Циклы со счетчиком
Задача 1.4. Графические формы
DefSng x – y
Private Sub
Scale ( -10, 12 ) – ( 10, -12 )
x1 = -8: y1 = 6: x2 = 0: y2 = 10: x3 = 8: y3 = 6:
x4 = 8: y4 = -6: x5 = 0: y5 = -10: x6 = -8: y6 = -6
k = 0.1
For i % = 1 To 50
Line ( x1, y1 ) – ( x2, y2 ), vbGreen
Line ( x2, y2 ) – ( x3, y3 ), vbRed
Line ( x3, y3 ) – ( x4, y4 ), vbYellow
Line ( x4, y4 ) – ( x5, y5 ), vbWhite
Line ( x5, y5 ) – ( x6, y6 ), vbCyan
Line ( x6, y6 ) – ( x1, y1 ), vbMagenta
x0 = x1: y0 = y1
x1 = x1 + ( x2 – x1 ) * k: y1 = y1 + ( y2 – y1 ) * k
x2 = x2 + ( x3 – x2 ) * k: y2 = y2 + ( y3 – y2 ) * k
x3 = x3 + ( x4 – x3 ) * k: y3 = y3 + ( y4 – y3 ) * k
x4 = x4 + ( x5 – x4 ) * k: y4 = y4 + ( y5 – y4 ) * k
x5 = x5 + ( x6 – x5 ) * k: y5 = y5 + ( y6 – y5 ) * k
x6 = x6 + ( x0 – x6 ) * k: y6 = y6 + ( y0 – y6 ) * k
Next i
End Sub
Результат работы нашей программы - изображение спирали, которое возникает при вращении постепенно поворачивающегося и уменьшающегося многоугольника.
Изменив некоторые параметры в программе можно получить интересные эффекты в изображении. Например, коэффициенту к присвоить значение 0,9 и счетчик установить до 100 единиц.
Капитан команды «Почемучки»:
В практической профессиональной деятельности могут пригодиться навыки дизайнерского мастерства. Одним из элементов художественного оформления могут стать графические формы.
Вопрос: Как подбирается цветовая гамма?
Ответ: Цвета линий подбираются согласно вашим предпочтениям. Например, если вы хотите заменить белую линию на черную, то в программе оператор vbWhite заменяется на vbBlack.
Учитель:
Право представить свой проект предоставляется команде «Буквоежки».
Капитан команды «Буквоежки»:
Наша команда работала над проектом, тема которого «Программирование повторений с помощью цикла с условием».
В рамках нашего проекта мы представляем две задачи:
1. Модель стрельбы по мишени.
2. Модель броуновского движения.
1-ый участник команды «Буквоежки»:
При программировании повторяющихся действий далеко не всегда заранее известно число повторений. Поэтому для решения задач применяется цикл с условием – многострочный оператор, первая строка которого начинается с ключевого слова Do (выполнить), а последняя строка начинается с ключевого слова Loop (петля).
2-ой участник команды «Буквоежки»:
Решение поставленной задачи – моделирование стрельбы по мишени, расположенной на экранной форме. Мишень – это круг в центре этой формы. Начало воображаемой стрельбы – это щелчок командной кнопки, после которой переменные х и y будут циклически получать конкретные значения – координаты точки на экранной форме, куда угодила пуля. Воображаемая стрельба будет вестись до тех пор, пока мишень не будет поражена определенным числом воображаемых пуль.
Выстрелы будут фиксироваться с помощью метода PSet, который будет рисовать точки на экранной форме.
А попадания будут фиксироваться с помощью проверки условия x2 + y2 <= R ( R – радиус круглой мишени ).
Проект № 2. Циклы с условием
Задача 2.1. Моделирование стрельбы по мишени
Private Sub
Dim ЧислоВыстрелов As Integer, ЧислоПопаданий As Integer
Command1.Visible = False: Refresh
Scale (-8, 5)-(8, -5)
Cls
Circle (0, 0), 1, vbYellow
FillStyle = 0
FillColor = vbYellow
Randomize
ЧислоВыстрелов = 0: ЧислоПопаданийний = 0
Do Until ЧислоПопаданий = 1
ЧислоВыстрелов = ЧислоВыстрелов + 1
x = -8 + 16 * Rnd: y = -5 + 10 * Rnd
If x ^ 2 + y ^ 2 <= 1 Then ЧислоПопаданий = ЧислоПопаданий + 1
PSet (x, y), vbRed
DrawWidth = 10
Loop
Command1.Visible = True
End Sub
Капитан команды «Буквоежки»:
При решении задачи «Моделирование стрельбы по мишени» прослеживается связь между «Информатикой» и «Теорией вероятности».
В практической деятельности может пригодиться умение создавать модели различных явлений и процессов.
Вопрос: Можно ли увеличивать диаметр мишени?
Ответ: Да, можно. Для этого в операторе Circle, который изображает мишень, необходимо изменить величину радиуса окружности. Например Circle (0,0), 5, vbYellow.
Вопрос: Известно ли заранее число выстрелов по мишени?
Ответ: Нет, количество выстрелов предугадать невозможно. Это может быть один выстрел и сразу чёткое попадание в мишень, а может быть десять или двадцать выстрелов. Стрельба прекращается, как только выполняется условие x ^ 2 + y ^ 2 <= 1.
3-ий участник команды «Буквоежки»:
Перед нами стояла задача - написать программу, с помощью которой имитируется броуновское движение, - движение очень маленькой частицы под воздействием ударов молекул, при котором частица перемещается рывками, случайным образом меняя направление и скорость своего движения. При этом траектория частицы – причудливая ломаная линия. Программа должна вычерчивать такую траекторию – рисовать каждый последующий отрезок случайным образом, независимо от того, каким был предыдущий отрезок. Случайно должно выбираться направление движения и скорость движения.
Проект № 2. Циклы с условием
Задача 2.2. Создание модели броуновского движения
Private Sub
Picture1. Scale ( -50, 50 ) – ( 50, -50 )
Randomize
Form1. Cls: Picture1. Cls
k # = 0
For i % = 1 To 5
x ! = 0: y ! = 0: c % = 10 * Rnd
Do Until x < -50 Or x > 50 Or y < -50 Or y > 50
For t & = 1 To 100000
Next t
k = k + 1
r ! = 10 * Rnd
f ! = 6.28 * Rnd
xn ! = x: x = x + r * Cos ( f )
yn ! = y: y = y + r * Sin ( f )
Picture1.Line ( x, y ) – ( xn, yn ), QBColor (c)
Picture1.DrawWidth = 5
Loop
Next i
Form1. Print
End Sub
Капитан команды «Буквоежки»:
Из курса физики мы знаем, что такое движение впервые описал английский ботаник Р.Броун в 1827 г., наблюдая за перемещением частиц пыльцы растений в жидкости. Сегодня мы создали компьютерную модель броуновского движения.
Вопрос: Каким образом достигается случайный выбор направления движения частицы?
Ответ: Для этой цели используется оператор рандомизации Randomize, который обеспечивает случайный выбор направления движения. Используя этот оператор и соответствующие формулы, обеспечивается случайный выбор направления движения и длины каждого отрезка.
Вопрос: Почему траектории движения частиц изображаются разными цветами?
Ответ: Одним из способов задания цвета является применение функции QBColor (с), где с – код цвета. Аргумент c программа выбирает случайно благодаря уже упомянутой функции Randomize.
Учитель:
Итак, обе команды работали в рамках общей темы «Повторения и циклы». Команда «Почемучки» более глубоко изучила раздел «Циклы со счётчиком», а команда «Буквоежки» подробно рассмотрела раздел «Циклы с условием». Результатом этой работы стали два проекта, которые сегодня были представлены. Давайте подведем предварительные итоги и сделаем выводы:
Умение программировать можно применять для построения графиков функций: парабол, гипербол, прямых, тригонометрических и других. Преимущество компьютерного оформления в том, что графики изображается практически идеально. Можно варьировать масштаб, цвет, толщину линий. Распечатанными с помощью принтера графиками функций можно оформить работы по математике, стенды, контрольные и курсовые работы.
Важным моментом является возможность моделировать поведение каждой из функций при изменении аргументов и параметров. Таким образом, компьютер становится нашим помощником в изучении математики.
Для молодого специалиста важным аргументом при устройстве на работу является наличие знаний и навыков работы в области компьютерного дизайна. Создание учебных рекламных проектов расширяет кругозор, развивает наши творческие способности.
Увлечение программированием способствует более глубокому изучению других предметов. Возможно, первокурсникам на уроках физики будет интересно наблюдать нашу модель броуновского движения.
Работа над проектом – это командная работа, которая учит, как правильно распределить задание, найти взаимопонимание, вовремя помочь друг другу.
Предлагаю объединить команды «Почемучки» и «Буквоедки» под новым названием «Знатоки» и совместно работать над новым интересным проектом.
3). Подведение итогов (4 минуты).
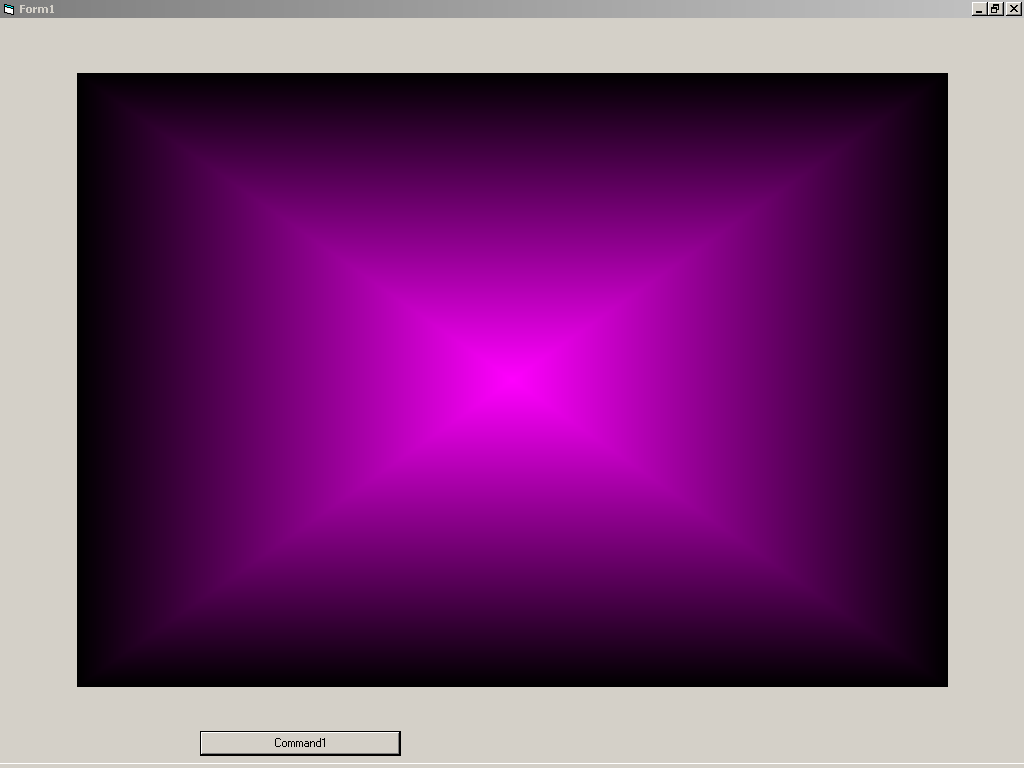
Проект № 1. Циклы со счетчиком
Задача 1.1. Демонстрация метода Line.
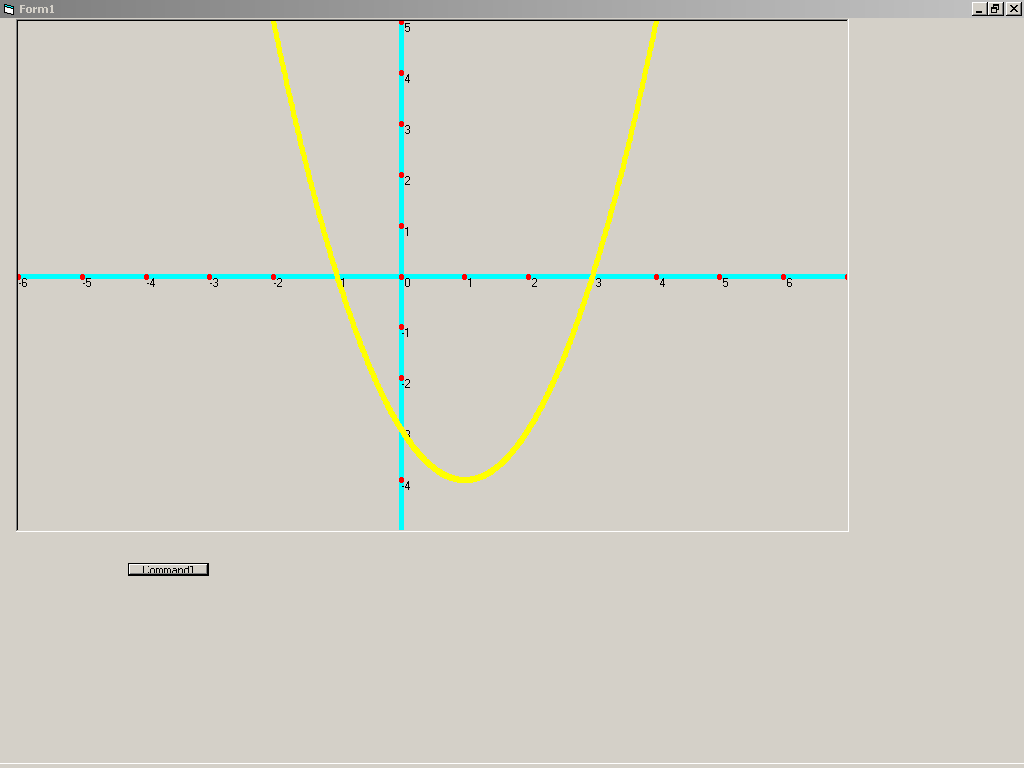
Проект № 1. Циклы со счетчиком
Задача 1.2. Построение графика функции y = a * x ^ 2 + b * x + c ,
где a = 1, b = -2, c = -3.
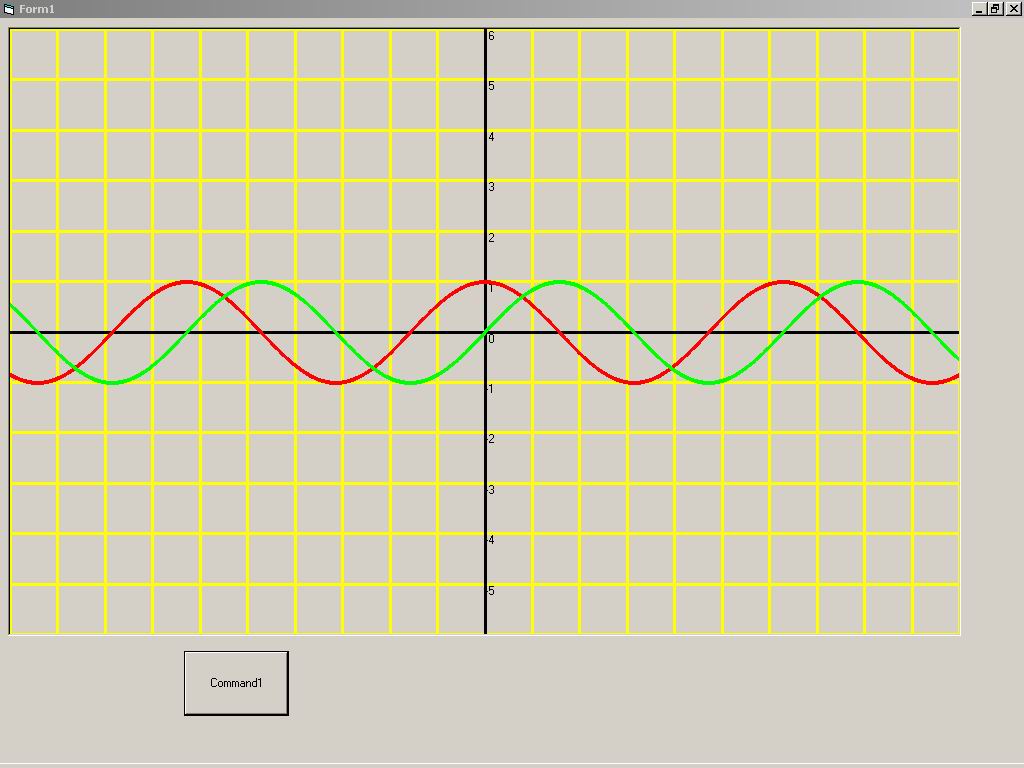
Проект № 1. Циклы со счетчиком
Задача 1.3. Построение тригонометрических функций
( y = sin ( x ), y = cos ( x )).
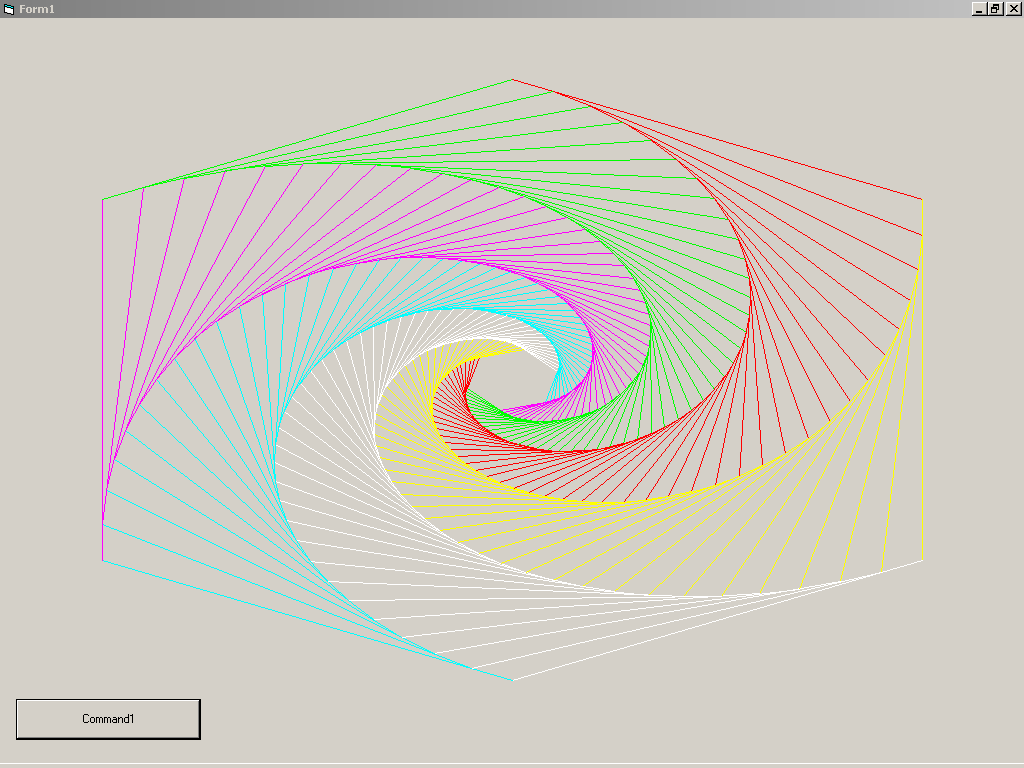
Проект № 1. Циклы со счетчиком
Задача 1.4. Графические формы.

Проект № 2. Циклы с условием
Задача 2.1. Моделирование стрельбы по мишени.
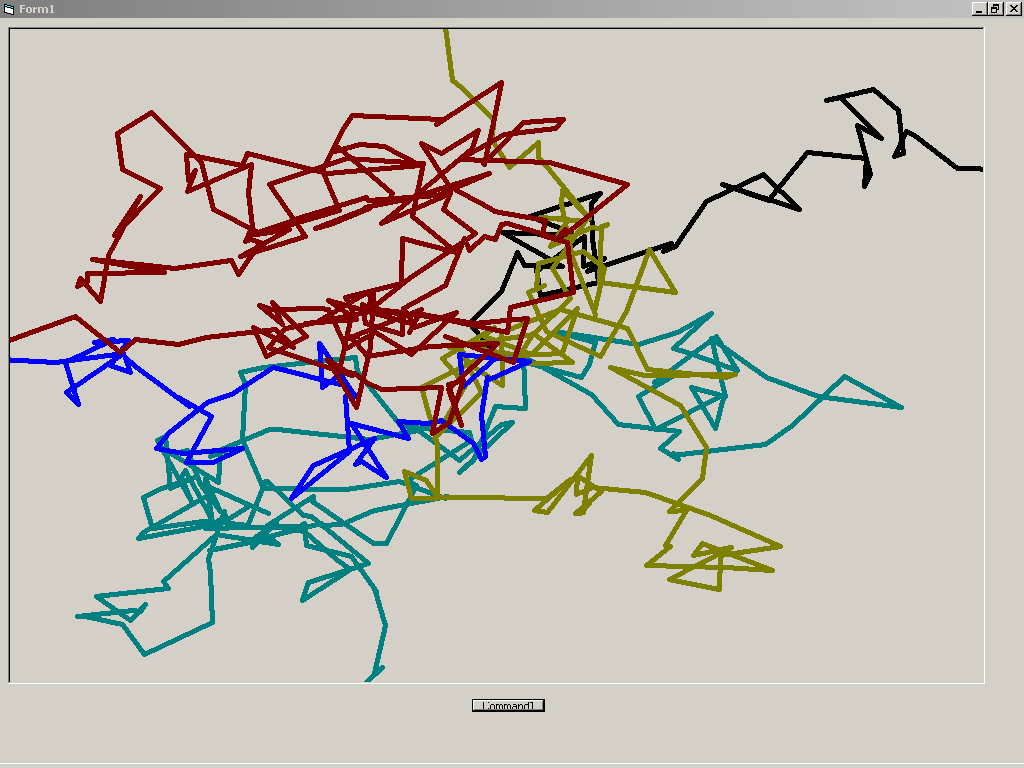
Проект № 2. Циклы с условием
Задача 2.2. Создание модели броуновского движения.
Список литературы:
Волчёнков Н.Г. Программирование на Visual Basic 6: В 3-х ч. Часть 1. – М.: ИНФРА-М, 2002. – 288 с.
Волчёнков Н.Г. Программирование на Visual Basic 6: В 3-х ч. Часть 2. – М.: ИНФРА-М, 2002. – 280 с.
Волчёнков Н.Г. Программирование на Visual Basic 6: В 3-х ч. Часть 3. – М.: ИНФРА-М, 2002. – 238 с.
Мухина С.А., Соловьева А.А. Нетрадиционные педагогические технологии в обучении. Ростов-на-Дону: Изд-во «Феникс», 2004. – 384 с.
Интернет-ресурсы:
http://vbbook.ru

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ