Аналіз експериментальних даних
 План
План
1. Дисперсійний аналіз
2. Кореляційний і регресійний аналіз
3.Парна регресія
Література
Аналіз експериментальних даних
В дослідженнях для обробки експериментальних даних найбільш широко застосовуються такі методи математичної статистики, як дисперсійний, кореляційний і регресійний аналіз.
1. Дисперсійний аналіз
Дисперсійний аналіз – основна задача – визначення впливу різних факторів на мінливість ознаки, яка вивчається. Наприклад урожай в польових умовах, успішність студентів. Загальне варіювання (мінливість) - 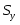 можна розчленувати на три основні частини:
можна розчленувати на три основні частини:
варіювання варіантів - 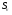 ;
;
варіювання повторів - 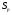 ;
;
випадкові варіювання - 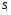
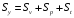 (1)
(1)
Особливостями дисперсійного аналізу є такі положення:
Замість середніх для окремих варіантів досліду обчислюється одна загальна середня арифметична для всього досліду в цілому.
Замість індивідуальних помилок середніх кожного варіанта досліду обчислюють одну усереднину похибку загальної середньої, яку використовують для оцінки розрізнювання варіантів.
Середню похибку досліду знаходять шляхом розкладання загальної дисперсії всіх даних досліду на складові частини, які характеризують варіювання, яке пов’язане з факторами, які вивчаються в досліді, і варіювання випадкове, яке обумовлене різноманітним випадковим впливом зовнішніх умов на мінливість при знаків і властивостей, які вивчаються.
Визначення випадкового варіювання часто є основною задачею дисперсійного аналізу. Воно дає можливість визначити помилку досліду і найменшу суттєву різницю (Н С Р), тобто ту мінімальну різницю між середніми, яка в даному експерименті є суттєвою
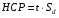
де t – критерій Стьюдента для прийнятого рівня значущості і числа ступенів волі залишкової дисперсії (береться з таблиці).
Sd – похибка різниці обчислюється за формулою

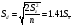 (2)
(2)
де n – число, що повторюється в порівняльних варіантах;
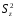 - залишковий середній квадрат (дисперсія помилок);
- залишковий середній квадрат (дисперсія помилок);
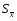 - узагальнена помилка середньої
- узагальнена помилка середньої
Вибираємо 5% рівень значущості, що означає, що похибка може повторитися 5 раз із 100.
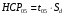 (3)
(3)
2. Кореляційний і регресійний аналіз
Якщо необхідно визначити залежність між двома або декількома признаками і встановити їх взаємний зв’язок використовують кореляції і регресії. Теорія кореляції вивчає взаємозв’язок між величинами, які досліджуються. Діалектичний підхід до вивчення природи і суспільства вимагає розглядати явища у взємозв’язку і в неперервному змінюванні. Теорія кореляції дозволяє виразити ці взаємозв’ки у кількісній формі.
Найбільш простим видом зв’язку між величинами є функціональна залежність, коли кожному значенню однієї величини відповідає одне конкретно визначене значення другої величини.
До функціональних зв’зків відноситься наприклад, залежність між об’ємом води W, часом t і використанням Q:
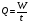 (4)
(4)
Якщо змінна величина у змінюється в залежності від іншої змінної х, але на зміну у впливає багато інших факторів, врахувати які інколи не в змозі, то тоді кожному значенню х відповідає декілька значень у. Такі зв’зки називаються кореляційними, або зв’язок між змінними величинами х і у називається кореляційним, якщо різним значенням однієї із них (х) відповідають групові середні другої (у) або навпаки. В таких випадках одна величина розглядається як незалежна змінна і називається аргументом (х), а друга – залежна змінна і називається функцією (у). Загальний вигляд рівняння кореляційного зв’язку y=f(x), де х - аргумент, у – функція.
При графічному зображенні статистичного звя’зку часто точки розміщують так, що можна провести ряд ліній різноманітного типу.
Після встановлення форми зв’язку і її типу визначають її тісноту. В якості числового показника зв’язку простої лінійної кореляції використовують коефіцієнт кореляції
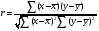 (5)
(5)
де 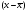 і
і 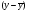 - відхилення значень х і у від своїх середніх
- відхилення значень х і у від своїх середніх 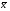 і
і 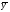 в п порівнювальних парах.
в п порівнювальних парах.
Стандартну похибку коефіцієнта кореляції визначають з рівняння
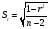 (6)
(6)
r – коефіцієнт кореляції; п – число пар значень, за якими обчислений коефіцієнт кореляції. Значення коефіцієнта кореляції записується разом з його похибкою у вигляді 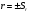 . Критерій суттєвого коефіцієнта кореляції t обчислюють з рівняння
. Критерій суттєвого коефіцієнта кореляції t обчислюють з рівняння
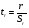 або
або 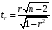 (7)
(7)
Зіставлення фактичного і теоретичного (табличного) значень t при числі ступеню волі п-2 дає можливість оцінити суттєвість r при тому чи іншому рівню значущості.
Якщо 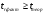 , то кореляційний зв’язок існує, а якщо
, то кореляційний зв’язок існує, а якщо 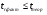 - не існує.
- не існує.
Поряд з коефіцієнтом кореляції для характеристики зв’язку між двома ознаками використовують коефіцієнт детермінації 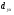 , який чисельно рівний квадрату коефіцієнта кореляції:
, який чисельно рівний квадрату коефіцієнта кореляції:
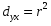 (8)
(8)
Коефіцієнт детермінації показує частину тих змін, які у залежності, яку вивчають обумовлені факторіальними ознаками і дають більш чітке уявлення про ступінь спряження ознак. Наприклад, якщо коефіцієнт кореляції рівний 0,20 – 0,30, то коефіцієнт детермінації 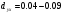 тобто тільки 4-9% всіх вимірів однієї ознаки пов’язані із змінами другої. При
тобто тільки 4-9% всіх вимірів однієї ознаки пов’язані із змінами другої. При 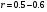 число зв’язків збільшується до 25-30% і тільки при
число зв’язків збільшується до 25-30% і тільки при 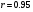 біля 97% зміна результативної ознаки пов’язано із змінами факторіального.
біля 97% зміна результативної ознаки пов’язано із змінами факторіального.
Кореляційне відношення обчислюється
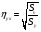 (9)
(9)
де η – кореляційне відношення; Sv – сума квадратів відхилення за варіантами;
Sy – загальна сума квадратів.
Кореляційне відношення використовується для оцінки криволінійної форми зв’зку між ознаками і має додатній знак, змінюється від 0 до 1.
При малому числі спостережень кореляційне відношення обчислюється:
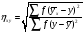 (10)
(10)
де 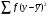 - сума квадратів відхилень групових і середніх
- сума квадратів відхилень групових і середніх 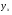 від загальної середньої
від загальної середньої 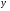 (групове варіювання), яка характеризує ту частину варіювання ознаки
(групове варіювання), яка характеризує ту частину варіювання ознаки 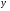 , яка пов’язана з мінливістю ознаки
, яка пов’язана з мінливістю ознаки 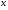 .
.
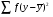 - сума квадратів різниці між кожним значенням і загальною середньою
- сума квадратів різниці між кожним значенням і загальною середньою 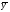 , яка характеризує загальне варіювання ознаки
, яка характеризує загальне варіювання ознаки 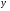 .
.
Похибка 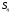 і критерій істотного кореляційного відношення обчислюється за рівнянням:
і критерій істотного кореляційного відношення обчислюється за рівнянням:
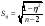 ;
; 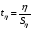 (11)
(11)
Фактичне значення 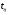 порівнюють з теоретичним, який приймається для вибраного рівня значущості при числі ступенів волі
порівнюють з теоретичним, який приймається для вибраного рівня значущості при числі ступенів волі 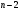 з таблиці. Якщо
з таблиці. Якщо 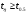 , то кореляційне відношення суттєве.
, то кореляційне відношення суттєве.
Квадрат кореляційного відношення називають індексом детермінації:
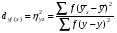 (12)
(12)
Він показує ту долю варіювання ознаки 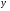 , яка обумовлена змінами ознаки
, яка обумовлена змінами ознаки 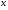 .
.
Обчисливши коефіцієнт кореляції можна отримати загальну уяву про спряження ознак які вивчаються.
Регресійний аналіз – наукове дослідження закономірностей між явищами, які залежать від багатьох факторів. Мета його – відшукати рівняння лінії, яка найбільш точно виражає залежність однієї ознаки від іншої. За формою регресія може бути прямолінійною і криволінійною, а за характером – простою, коли змінювання вислідної ознаки відбувається під зміною однієї факторіальної ознаки, і множинною, коли зміна обумовлена декількома факторіальними ознаками.
Регресивний аналіз дозволяє передбачити можливість зміни однієї ознаки на основі відомих змін другої шляхом розрахунку емпіричних формул, які показують, що зв’язок між ними існує.
При лінійній регресії залежність між ознаками виражається коефіцієнтом регресії, який показує в якому напрямку і на яку величину змінюється одна ознака при зміні другої на одиницю виміру.
Обчислюється коефіцієнт регресії за рівняннями:
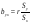 ;
; 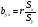 . (13)
. (13)
Де  - коефіцієнт кореляції;
- коефіцієнт кореляції;
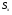 і
і 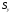 - середні квадратичні відхилення;
- середні квадратичні відхилення;
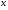 і
і 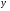 вивчаються у рядах.
вивчаються у рядах.
Коефіцієнти регресії мають знак коефіцієнта кореляції:
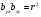 (14 )
(14 )
Ця властивість використовується для перевірки чи правильно обчислений коефіцієнт регресії.
Похибку коефіцієнтів регресії обчислюють за рівнянням:
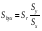 і
і 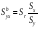 . (15)
. (15)
Критерій суттєвості коефіцієнта регресії дорівнює критерію суттєвості коефіцієнта кореляції, тобто:
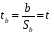 (16)
(16)
Часто залежність між признаками, які вивчаються буває криволінійною, вона може мати різні форми і описується відповідними рівняннями. В цьому випадку, головна задача регресійного аналізу полягає в тому, щоб по характеру розпреділення точок на графіку підібрати аналітичну залежність, яка описує закономірність зміни ознак. Після того, Як аналітична залежність підібрана, необхідно математичними перетвореннями привести її до рівняння прямої лінії, тобто перетворити вихідні дані і обчислити значення параметрів, які входять в аналітичну залежність. Приведення криволінійної залежності до рівняння прямої лінії дозволяє використати прийоми регресійного аналізу.
Приклад.
Техніку приведення кореляційного і регресійного аналізу розглянемо на прикладі для невеликого числа спостережень (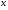 ) від змінної (
) від змінної (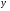 ).
). 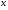 - вологість грунту;
- вологість грунту; 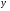 - наліплювання грунту.
- наліплювання грунту.
Розрахунки зручно вести складаючи таку таблицю.
Розрахунки допоміжних величин для обчислення кореляції і регресії 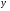 по
по 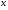 .
.
№
пари
Значення ознаки

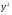
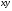
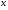 (%)
(%)
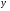 (г/см2)
(г/см2)
1
2
3
4
5
6
7
8
9
10
11
12
Сума
19,9
20,9
26,1
29,4
30,5
40,3
44,8
47,8
55,6
58,3
64,5
76,6
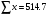
0,0
0,6
1,1
1,2
1,7
1,7
2,6
3,4
4,2
5,8
6,3
7,3

396,01
436,81
681,21
864,36
930,25
1624,09
2007,04
2284,84
3091,36
3398,89
4160,25
5867,56
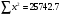
0,00
0,36
1,21
1,44
2,89
2,89
6,76
11,56
17,64
33,64
39,69
53,29
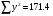
0,00
12,54
28,71
35,28
51,85
68,51
116,48
162,52
233,52
338,14
406,35
559,18
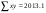
Розв’язання:
За даними таблиці обчислюємо шість допоміжних величин:
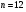 ;
;
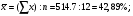
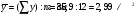
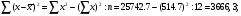
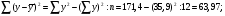
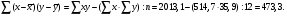
Обчислюється коефіцієнт кореляції, регресії і рівняння регресії:
коефіцієнт кореляції
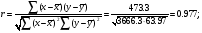
коефіцієнт регресії 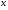 і
і 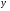
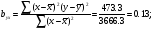
Рівняння регресії
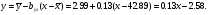
Таким чином шукана залежність має вигляд: 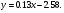
Визначається похибка і критерій значущості для коефіцієнта кореляції:
Похибка коефіцієнта кореляції
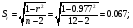
критерій значущості коефіцієнта кореляції
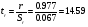
Фактичне значення
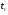 порівнюється з теоретичним
порівнюється з теоретичним 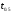 , яке приймається рівним: 8-9 ступенів волі (при
, яке приймається рівним: 8-9 ступенів волі (при 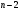 - це 10-11 пар спостережень) – 2,3; для 10-14 ступенів волі – 2,2; для 15-24 ступенів волі – 2,1; для 25-100 ступенів волі – 2,0. Кореляція і регресія визначається суттєвою, якщо
- це 10-11 пар спостережень) – 2,3; для 10-14 ступенів волі – 2,2; для 15-24 ступенів волі – 2,1; для 25-100 ступенів волі – 2,0. Кореляція і регресія визначається суттєвою, якщо 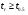 . В нашому прикладі
. В нашому прикладі 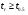 , так як
, так як 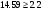 . Значить між вологістю грунту і її налипання є суттєвий прямий зв’язок.
. Значить між вологістю грунту і її налипання є суттєвий прямий зв’язок.За отриманим рівнянням регресії обчислюють теоретичне значення
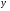 для крайніх величин
для крайніх величин 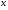 (19,9 і 76,6, згідно таблиці)
(19,9 і 76,6, згідно таблиці)
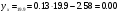 ;
;
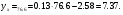
Знайдені точки (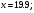
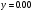 і
і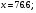
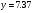 ) наносяться на графіці, з’єднуючи їх прямою, маємо теоретичну лінію регресії. Вона показує, що збільшення вологості грунту на 1% відповідає збільшенню налипання на 0,13 г/см2.
) наносяться на графіці, з’єднуючи їх прямою, маємо теоретичну лінію регресії. Вона показує, що збільшення вологості грунту на 1% відповідає збільшенню налипання на 0,13 г/см2.
3. Парна регресія
Парна залежність може бути апроксимована прямою лінією, параболою, гіперболою, логарифмічною, степеневою або показниковою функцією,поліномом і інше.
Рис. Вигляди основних ліній різних зв’язків між змінними величинами і їх рівняння.
Пряма, яка проходить через початок координат має рівняння
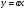 (3,а).
(3,а).Пряма, що не проходить через початок координат має рівняння
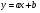 , або
, або 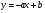 . Ці залежності вимагають визначення двох параметрів
. Ці залежності вимагають визначення двох параметрів 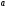 і
і 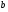 . (3, б, в).
. (3, б, в).Парабола з вершиною в початку координат і симетрична одній із осей має рівняння
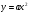 . Формула один параметр
. Формула один параметр 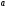 із зменшенням якого зменшується розхил параболи (рис.3, г).
із зменшенням якого зменшується розхил параболи (рис.3, г).Парабола, симетрична прямій паралельній осі
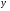 має рівняння
має рівняння 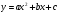 . Функція квадратична. У формулі необхідно визначити три параметра:
. Функція квадратична. У формулі необхідно визначити три параметра: 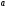 ,
, 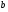 і
і 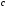 (рис.3, д, є).
(рис.3, д, є).Гіпербола, асимптотично наближається до осей координат, рівняння має вигляд
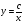 , необхідно визначити параметр
, необхідно визначити параметр 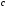 (рис.3, ж).
(рис.3, ж).Гіпербола асимптотично наближається до прямих, паралельних до осей координат, рівняння має вигляд
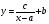 . Параметри
. Параметри 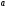 і
і 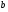 є координатами точки
є координатами точки 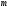 . Знак параметра
. Знак параметра 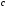 залежить від розміщення гіперболи по відношенню до асимптот (рис.3, з).
залежить від розміщення гіперболи по відношенню до асимптот (рис.3, з).Степеневі криві (рис.3, и, к), рівняння
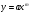 , де
, де 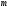 може бути додатнім, цілим або дробовим.
може бути додатнім, цілим або дробовим.Показникові крива, коли із зростанням однієї величини
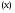 спостерігається підсилене зростання
спостерігається підсилене зростання 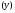 . Рівняння
. Рівняння 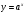 (рис.8.3, л).
(рис.8.3, л).
Двох факторне поле можна апроксимувати, площиною, параболоїдом другого порядку, гіперболоїдом. Для 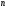 - змінних фактів зв’язок можна встановити за допомогою
- змінних фактів зв’язок можна встановити за допомогою 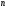 - мірного простору рівняннями другого порядку
- мірного простору рівняннями другого порядку
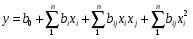 (17)
(17)
де 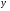 - функція мети багатофакторних змінних;
- функція мети багатофакторних змінних;
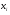 - незалежні фактори;
- незалежні фактори;
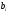 - коефіцієнт регресії, що характеризують вплив фактора
- коефіцієнт регресії, що характеризують вплив фактора 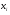 на функцію мети;
на функцію мети;
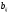 - коефіцієнти, які характеризують подвійний вплив факторів
- коефіцієнти, які характеризують подвійний вплив факторів 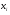 і
і 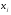 на функцію мети.
на функцію мети.
При побудові теоретичної регресійної залежності, оптимальною буде така функція, в якій виконуються умови найменших квадратів 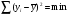 , де
, де 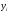 - фактичні координати поля;
- фактичні координати поля; 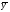 - середнє значення ординати з абсцисою
- середнє значення ординати з абсцисою 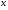 , обчисленою з рівняння. Після кореляції апроксимують рівнянням прямої. Лінію регресії розраховують з умови найменших квадратів:
, обчисленою з рівняння. Після кореляції апроксимують рівнянням прямої. Лінію регресії розраховують з умови найменших квадратів:
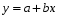 (18)
(18)
При цьому крива АВ найкращим чином вирівнює значення постійних коефіцієнтів 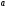 і
і 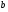 , тобто коефіцієнтів рівняння регресії. Їх обчислюють за формулами:
, тобто коефіцієнтів рівняння регресії. Їх обчислюють за формулами:
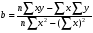 (19)
(19)
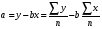 (20)
(20)
Критерієм близькості кореляційної залежності між 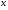 і
і 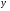 до лінійної функціональної залежності є коефіцієнт парної або просто коефіцієнт кореляції
до лінійної функціональної залежності є коефіцієнт парної або просто коефіцієнт кореляції  . Він просто показує ступінь лінійності зв’язку
. Він просто показує ступінь лінійності зв’язку 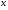 і
і 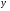 .
.
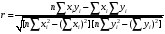 (21)
(21)
де 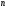 - число вимірів.
- число вимірів.
Задовільна тіснота зв’язку при 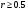 , добра при
, добра при 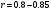 . Для визначення проценту мінливості шуканої функції
. Для визначення проценту мінливості шуканої функції 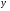 відносно її середнього значення, який визначається мінливістю фактора
відносно її середнього значення, який визначається мінливістю фактора 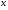 , обчислюють коефіцієнт детермінації
, обчислюють коефіцієнт детермінації
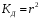 (22)
(22)
Рівняння регресії прямої записати таким виразом:
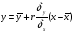 (23)
(23)
Література:
1. Белый И.В. и др. Основы научных исследований и технического творчества / И.В. Белый, К.П. Власов, В.Б. Клепиков. — Х,: Вища шк. Изд-во при Харьк. ун-те, 1989-200с.
2. Белуха Н.Т. Основы научных исследований в экономике. — К.: Вища шк. Головное изд-во, 1985.— 215с.
3. Вознюк С.Т. и др. Основы научных исследований. Гидромелиорация / Вознюк С.Т., Гончаров С.М., Ковалев С.В. — К.: Вища шк. Головное издательство, 1985-192с.
4. Воловик П.М. Теорія імовірностей і математична статистика в педагогіці —Х.: Вища шк., 1969-222с.
5. Гмурман В.Е. Теория вероятностей и математическая статистика. Изд. 4-е — М.: Высшая школа, 1972. — 367с.
6. Митропольский А.К. Техника статистических вычислений. М.: Наука, 1971, 576с.
7. Нечаев Ю.И. Основы научных исследований — Киев, Одесса: Вища шк. Головное изд-во, 1983, — 160с.
8. Румшиский Л.Э. Математическая обработка результатов эксперимента. М.: Наука, 1971,— 192с.
9. Сиденко В.М. Грушко И.М. Основы научных исследований. Харьков. Вища шк, 1977, — 240с.
10. Сытник В.Ф. Основы научных исследований. К.: Вища шк. Головное изд-во. 1978, — 184с.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ